三支面向属性概念格的构成

苏 新，夏文富，陈永平

(1.马鞍山职业技术学院电子信息系，安徽马鞍山 243011；2.杭州市地铁集团有限责任公司运营分公司，浙江杭州 310000)

形式概念是由德国数学家Gante 等于1982 年提出的，其主要思想是通过概念之间的泛化和例化关系，揭示数据之间的内部关系和对象及属性之间的关系。目前，形式概念分析已在数据挖掘、专家系统、软件工程等领域得到广泛应用。传统的形式概念分析理论研究的是对象(属性)共同具有的属性(对象)，或是对象(属性)共同不具有的属性(对象)。反映在实际应用中，就是针对某一观点，要么接受，要么拒绝，这与某些实际应用不相符。因此，Yao提出三支决策理论，基于接受和拒绝外，增加了一种延迟决策方法。Qi等将三支决策理论和形式概念分析理论相结合，提出了三支概念分析理论。三支概念格理论包括由对象诱导的三支概念格(OE-概念格)和由属性诱导的三支概念格(AE-概念格)。钱婷将面向对象(属性)概念格理论和三支概念分析相结合，提出了三支面向对象(属性)概念格。

关于三支概念格的构造，由于三支概念的数量庞大，文献[10]中在经典概念格上定义一个等价映射，并求出每个等价类及其最大元素，在此基础上给出三支概念格的构造算法；文献[11]中利用经典概念格及其补背景的并置和叠置得到混合形式背景，以此生成OE-概念格和AE-概念格；文献[12]中主要针对三支概念格构造，定义候选三支概念和冗余三支概念，给出了在候选概念中满足三支概念的条件，但没有给出候选概念和三支概念格以及冗余概念和三支概念格之间的关系。目前，对于三支概念格生成方面的研究主要集中于OE-概念格和AE-概念格，对三支面向对象(属性)概念格的生成算法关注较少；利用并置和叠置的方法分别生成三支面向对象概念格和三支面向属性概念格，但需生成一个比原形式背景大得多的新的形式背景，增加了三支概念格生成时复杂性。鉴于此，研究三支面向属性概念格的构造算法，基于时间复杂度的角度对其进行分析，以期提高算法效率。

1 预备知识

定义1设一个三元组

L

= (

G

,

M

,

I

)是一个形式背景，其中：

G

={

g

,

g

,…,

g

}，为一个对象集，

g

(

i

≤

n

)为一个对象；

M

= {

m

,

m

,

m

,…,

m

}，为属性集，每个

m

(

j

≤

q

)为一个属性；

I

为

G

和

M

之间的二元关系，即

I

⊆

G

×

M

。若(

g

,

m

) ∈

I

，则称

g

具有属性

m

，用1表示；若(

g

,

m

) ∉

I

，则称

g

不具有属性

m

，用0表示。对于形式背景(

G

,

M

,

I

)，在对象集

X

⊆

G

和属性集

Y

⊆

M

上定义*运算：

式中：

X

表示对象集

X

中所有对象共同具有的属性集合；

Y

表示拥有属性

Y

的对象集合；∀

g

∈

G

,∀

m

∈

M

。记{

g

}为

g

，{

m

}为

m

，称形式背景(

G

,

M

,

I

)是正则的，对任意

g

∈

G

,

g

≠∅,

g

≠

M

，且对任意

m

∈

M

,

m

≠∅,

m

≠

G

。定义2设(

G

,

M

,

I

)为形式背景，若

X

=

Y

且

Y

=

X

，则称(

X

,

Y

)是一概念，

X

为该概念的外延，

Y

为该概念的内涵。对于任意概念(

X

,

Y

)，(

X

,

Y

)，定义偏序关系为(

X

,

Y

)≤(

X

,

Y

)⇔

X

⊆

X

⇔

Y

⊆

Y

，则形式背景(

G

,

M

,

I

)的所有概念在该偏序关系下是完备格，形式背景(

G

,

M

,

I

)的概念格记为Lattices(

G

，

M

，

I

)，简写为

L

(

G

,

M

,

I

)。

以上定义的算子是形式背景中的正算子。

定义3设(

G

,

M

,

I

)为形式背景，对于

X

⊆

G

,

Y

⊆

M

，一对负算子定义如下：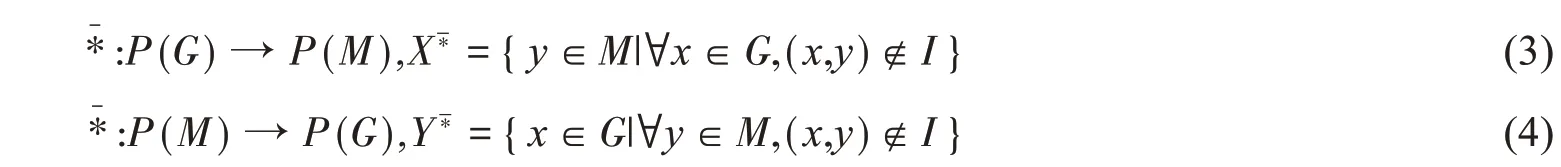

若

X

=

Y

且

Y

=

X

，则称(

X

,

Y

)为负概念，形式背景(

G

,

M

,

I

)在负算子下生成的所有负概念的集合也称为补概念集合，记为Negative Lattices(

G

,

M

,

I

)，简写为

L

(

G

,

M

,

I

)，在上述的偏序关系下

L

(

G

,

M

,

I

)也是完备格。根据形式背景(

G

,

M

,

I

)的补背景的定义，易得到形式背景(

G

,

M

,

I

)的负算子-*是其补背景(

G

,

M

,

I

)(

I

=

G

×

M

I

)的正算子，因此

L

(

G

，

M

，

I

)=

L

(

G

,

M

,

I

)。定义4对于形式背景(

G

,

M

,

I

)，引入一对近似算子，分别用□和⋄表示。对于∀

X

⊆

G

及∀

Y

⊆

M

，有

X

={

m

|∀∈

M

,

m

⊆

X

},

X

={

m

|∀

m

∈

M

,

m

⋂

X

≠∅}；对应的，对于∀

Y

⊆

M

，有

Y

={

g

|∀

g

∈

G

,

g

⊆

Y

},

Y

={

g

|∀

g

∈

G

,

g

⋂

Y

≠∅}。定义5设

K

=(

G

,

M

,

I

)为形式背景，如果∀

X

⊆

G

,∀

Y

⊆

M

，满足

X

=

Y

,

Y

=

X

，则称二元组(

X

，

Y

)为面向属性概念。其中：

X

为面向属性概念的外延；

Y

为面向属性概念的内涵。由形式背景(

G

,

M

,

I

)产生的全体面向属性概念的集合称为形式背景(

G

,

M

,

I

)的面向属性概念格，记为Attribute Lattices(

G

,

M

,

I

)，简写为

L

(

G

，

M

，

I

)。设

K

=(

G

,

M

,

I

)为一形式背景，

L

(

K

)为一完备格，其中的偏序关系为(

X

,

Y

)≤(

X

,

Y

)⇔

X

⊆

X

(

Y

⊆

Y

)，在

L

(

G

,

M

,

I

)中的运算为：

L

(

G

,

M

,

I

)中的每个概念都是面向属性概念，且(

L

(

G

,

M

,

I

)，≤)为完备格，称

L

(

G

,

M

,

I

)为形式背景(

G

,

M

,

I

)的面向属性概念格。定义6对于形式背景(

G

,

M

,

I

)，分别定义□和⋄的负算子如下：

进一步定义该三支算子的逆算子如下：

其中：

DP

(

G

) =

P

(

G

) ×

P

(

G

)；

DP

(

M

) =

P

(

M

) ×

P

(

M

)。定义8对于形式背景(

G

,

M

,

I

)，

X

,

Y

⊆

G

,

A

⊆

M

，如果

A

=(

X

,

Y

)且

A

=(

X

,

Y

)，则称((

X

，

Y

)，

A

)为形式背景(

G

,

M

,

I

)的由属性诱导的三支面向属性概念，记为Attribute-induced Lattices-概念，简写为AEL-概念，其中(

X

，

Y

)和

A

分别称为AEL-概念的外延和内涵。所有AEL-概念构成的集合称为形式背景(

G

,

M

,

I

)的由属性诱导的三支面向属性概念格，记为All Attribute-induced Lattices(

G

,

M

,

I

)，简写为

L

(

G

,

M

,

I

)，若((

X

，

Y

)，

A

)，((

Z

，

W

)，

B

)为形式背景(

G

,

M

,

I

)的AEL-概念，则定义偏序关系((

X

,

Y

),

A

)≤((

Z

,

W

)，

B

) ⇔(

X

,

Y

) ⊆(

C

,

D

) ⇔

A

⊆

B

。定 理1对 于 形 式 背 景(

G

,

M

,

I

)，对 于 任 意 的((

X

，

Y

)，

A

)，((

Z

，

W

)，

B

)∈

L

(

G

，

M

，

I

)，如 果 满 足((

X

,

Y

),

A

) ∧((

Z

,

W

),

B

) =((

X

,

Y

) ⋂(

Z

,

W

),(

A

⋂

B

))和((

X

,

Y

),

A

)∨((

Z

,

W

),

B

)=(((

X

,

Y

)⋃(

Z

,

W

)),(

A

⋃

B

))，那么称(

L

(

G

,

M

,

I

)，≤）构成完备格。形式背景(

G

,

M

,

I

)的所有AEL-概念在该偏序关系下是完备格，举例如下。例1 形式背景(

G

,

M

,

I

)中，

G

={1，2，3，4,5}，

M

={

a

，

b

，

c

，

d

},任意(

g

，

m

)∈

I

时，用1 表示；任意(

G

，

m

)∉

I

时，用0表示，如表1。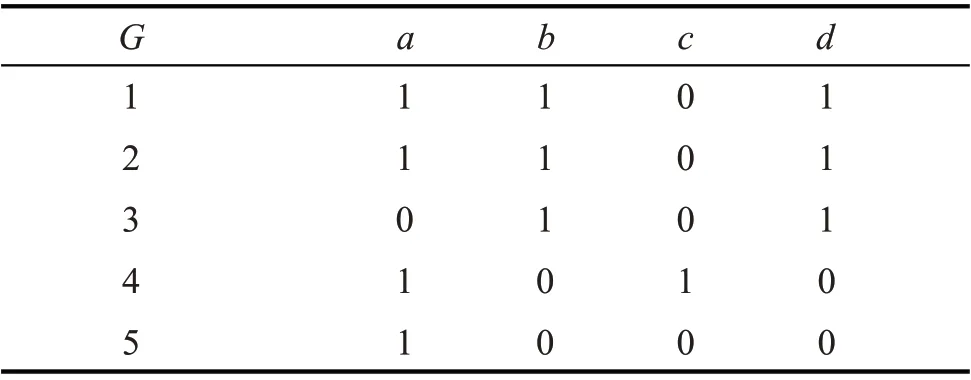

表1 形式背景(G，M，I)Tab.1 Formal contexts(G,M,I)

形式背景(

G

,

M

,

I

)对应的面向属性概念格

L

(

G

,

M

,

I

)和面向属性补背景概念格

L

(

G

,

M

,

I

)分别如图1，2。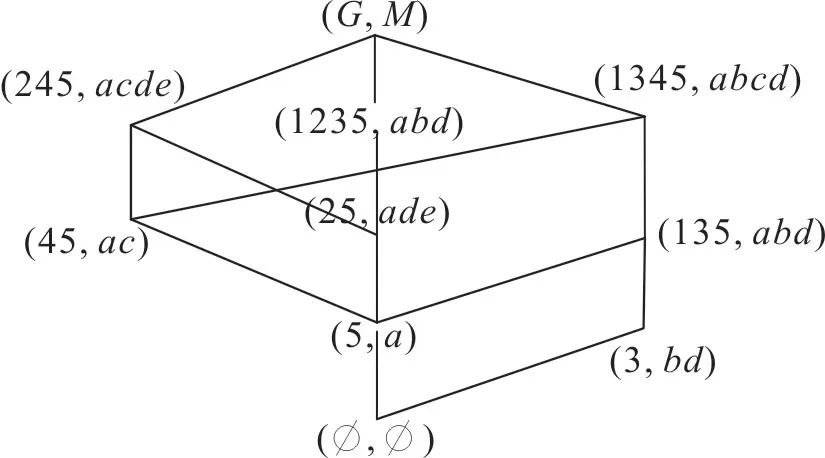

图1 例1中形式背景(G，M，I)的概念格Fig.1 LA(G，M，I)for example 1

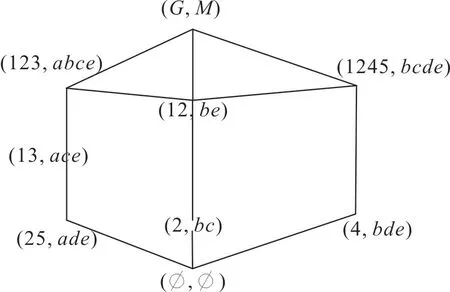
图2 例1中形式背景(G，M，I)的面向属性负概念格Fig.2 LNA(G，M，I)for example 1

2 由属性诱导的三支面向属性概念格的生成

在面向属性概念格及其补背景概念格的基础上，定义由属性诱导的三支面向属性极大概念集和极小概念集，并生成由属性诱导的三支面向属性概念。

定义9 假设

L

(

G

,

M

,

I

)和

L

(

G

,

M

,

I

)分别是形式背景(

G

,

M

,

I

)的面向属性概念格和面向属性的补背景概念格，对于任意(

X

，

Y

)∈

L

(

G

,

M

,

I

)，任意(

X

，

Y

)∈

L

(

G

,

M

,

I

)，(

X

，

Y

)和(

X

，

Y

)可以((

X

,

X

),

Y

⋃

Y

)的运算形式进行运算，称这样的运算为由属性诱导的三支面向属性的极大运算，用Δ表示。定义10 假设

L

(

G

,

M

,

I

)和

L

(

G

,

M

,

I

)分别是形式背景(

G

，

M

，

I

)的面向属性概念格和面向属性的补背景概念格，对于任意(

X

，

Y

)∈

L

(

G

,

M

,

I

)，任意(

X

，

Y

)∈

L

(

G

,

M

,

I

)，(

X

,

X

)Δ(

Y

,

Y

)=((

X

,

X

),

Y

⋃

Y

)被称为由属性诱导的三支面向性概念格的极大概念，所有由属性诱导的三支面向属性的极大概念组成的集合称为由属性诱导的三支面向属性的极大概念集，记为Max All Attribute-induced Set(

G

,

M

,

I

)，简写为

S

(

G

，

M

，

I

)。由属性诱导的三支面向属性的极大概念集

S

(

G

,

M

,

I

)和由属性诱导的三支面向属性概念格

L

(

G

,

M

,

I

)之间的关系如下。定理2 假设

L

(

G

,

M

,

I

)和

L

(

G

,

M

,

I

)分别是形式背景(

G

,

M

,

I

)的面向属性概念格和面向属性的补背景概念格，

S

(

G

,

M

,

I

)为形式背景(

G

,

M

,

I

)的由属性诱导的三支面向性的极大概念集，

L

(

G

,

M

,

I

)为形式背景(

G

,

M

,

I

)的由属性诱导的三支面向性概念格，则

L

(

G

,

M

,

I

) ⊆

S

(

G

,

M

,

I

)。证明 假设∀((

X

,

X

),

Y

) ∈

L

(

G

,

M

,

I

)，那么存在(

X

,

Y

)∈

L

(

G

,

M

,

I

)且(

X

,

Y

)∈

L

(

G

,

M

,

I

)。由面向属性概念格和其补背景概念格的定义可知

X

=

Y

,

Y

=

X

，

X

=

Y

,

Y

=

X

；根据由属性诱导的三支面向属性概念格的定义可知

Y

=(

X

,

X

)，

Y

=(

X

,

X

)，又

Y

=(

X

,

X

)=(

X

⋃

X

)。令

Y

=

X

,

Y

=

X

，有

Y

=

Y

⋃

Y

，因 此 有((

X

,

X

),

Y

⋃

Y

)∈

L

(

G

,

M

,

I

)，再 根 据 定 义10 可 知((

X

,

X

),

Y

⋃

Y

)∈

S

(

G

,

M

,

I

)，因 此

L

(

G

,

M

,

I

) ⊆

S

(

G

,

M

,

I

)。例2 例1中的

L

(

G

,

M

,

I

)中的概念(45，

ac

)和

L

(

G

,

M

,

I

)中的概念(13，

ace

)按照定义9得到极大概念((45，13)，

ace

)，可以得出((45，13)，

ace

)∈

S

(

G

,

M

,

I

)，同时也有((45，13)，

ace

)∈

L

(

G

,

M

,

I

)；而

L

(

G

,

M

,

I

)中的概念(5，

a

)和

L

(

G

,

M

,

I

)中的概念(2，

bc

)按照定义9 可得到极大概念((5，2)，

ace

)，易知((5，2)，

ace

)∈

S

(

G

，

M

，

I

)，但((5，2)，

ace

)∉

L

(

G

,

M

,

I

)。

定理2表明，由属性诱导的三支面向属性概念格包含在由属性诱导的三支面向属性的极大概念集中。

定义11 假设

L

(

G

,

M

,

I

)和

L

(

G

,

M

,

I

)分别是形式背景(

G

,

M

,

I

)的面向属性概念格和面向属性的补背景概念格，对于任意(

X

，

Y

)∈

L

(

G

,

M

,

I

)，任意（

X

，

Y

）∈

L

(

G

,

M

,

I

)，如果

X

⊂(

Y

⋃

Y

)或者

X

⊂(

Y

⋃

Y

)，那么称(

X

,

X

)Δ(

Y

,

Y

)=((

X

,

X

),

Y

⋃

Y

)为由属性诱导的三支面向属性的极小概念，称所有由属性诱导的三支面向属性的极小概念组成的集合为由属性诱导的三支面向属性的极小概念集，记为Min All Attributeinduced Set(

G

,

M

,

I

)，简写为

S

(

G

,

M

,

I

)。定理3

S

(

G

,

M

,

I

)⊆

S

(

G

,

M

,

I

)。证 明 假 设∀((

X

,

X

),

Y

⋃

Y

)∈

S

(

G

,

M

,),那 么 根 据 定 义11 存 在(

X

，

Y

)∈

L

(

G

,

M

,

I

)，(

X

，

Y

)∈

L

(

G

,

M

,

I

)，再根据定义9可知((

X

,

X

),

Y

⋃

Y

)∈

S

(

G

,

M

,

I

)，故有

S

(

G

,

M

,

I

)⊆

S

(

G

,

M

,

I

)。定理4

S

(

G

，

M

，

I

)为形式背景(

G

，

M

，

I

)的由属性诱导的三支面向属性的极小概念集，

L

(

G

，

M

，

I

)为形式背景(

G

,

M

,

I

)的由属性诱导的三支面向属性概念格，则

L

(

G

,

M

,

I

)⋂

S

(

G

,

M

,

I

)=∅。证 明 假 设∀((

X

,

X

),

Y

⋃

Y

)∈

S

(

G

,

M

,

I

)，由 定 义11 可 知

X

≠(

Y

⋃

Y

)，或 者

X

≠(

Y

⋃

Y

)，((

X

,

X

),

Y

⋃

Y

)∉

L

(

G

,

M

,

I

)，

L

(

G

,

M

,

I

)⋂

S

(

G

,

M

,

I

)=∅。定理3和定理4说明形式背景(

G

,

M

,

I

)的由属性诱导的三支面向属性的极小概念集

S

(

G

,

M

,

I

)包含在形式背景(

G

,

M

,

I

)的由属性诱导的三支面向属性的极大概念集

S

(

G

,

M

,

I

)中，但是和形式背景(

G

,

M

,

I

)的由属性诱导的三支面向属性概念格

L

(

G

,

M

,

I

)之间的交集为空。由例2 中求出的极大概念((5，2)，

ace

)可知，((5，2)，

ace

)∈

S

(

G

,

M

,

I

)，但((5，2)，

ace

)∉

L

(

G

,

M

,

I

)。定理5

S

(

G

,

M

,

I

)为形式背景(

G

,

M

,

I

)的由属性诱导的三支面向属性的极大概念集，

S

(

G

,

M

,

I

)为形式背景(

G

,

M

,

I

)的由属性诱导的三支面向属性的极小概念集，

L

(

G

,

M

,

I

)为形式背景(

G

,

M

,

I

)的由属性诱导的三支面向属性概念格，则有

L

(

G

,

M

,

I

) =

S

(

G

,

M

,

I

) -

S

(

G

,

M

,

I

)。证明 由定理3 和定理4 知，

L

(

G

,

M

,

I

) ⊆

S

(

G

,

M

,

I

) -

S

(

G

,

M

,

I

)，对于任意((

X

,

X

),

Y

⋃

Y

)∈

S

(

G

,

M

,

I

) -

S

(

G

,

M

,

I

)，有((

X

,

X

),

Y

⋃

Y

)∈

S

(

G

,

M

,

I

)，且 有

X

⊆(

Y

⋃

Y

)，

X

⊆(

Y

⋃

Y

)，因((

X

,

X

),

Y

⋃

Y

)∉

S

(

G

,

M

,

I

)，故

X

⊂(

Y

⋃

Y

)和

X

⊂(

Y

⋃

Y

)不成立；又因

X

=(

Y

⋃

Y

)和

X

=(

Y

⋃

Y

)，((

X

,

X

),

Y

⋃

Y

)∈

L

(

G

,

M

,

I

)，故

L

(

G

,

M

,

I

) =

S

(

G

,

M

,

I

) -

S

(

G

,

M

,

I

)。根据上述理论，可求得表1中形式背景(

G

,

M

,

I

)对应的由属性诱导的三支面向属性概念格

L

(

G

,

M

,

I

)，结果如图3。

图3 例1中形式背景(G，M，I)由属性诱导的三支面向属性概念格Fig.3 LAAE(G，M，I)for example 1

3 算法及算法分析

输入面向属性概念格

L

(

G

,

M

,

I

)和面向属性补背景概念格

L

(

G

,

M

,

I

)，输出由属性诱导的三支面向属性概念格

L

(

G

,

M

,

I

)。

假设形式背景(

G

,

M

,

I

)的对象个数为

s

、属性个数为

t

，本文算法是在已知形式背景(

G

,

M

,

I

)面向属性概念格及其补背景概念格的基础上，求解由属性诱导的三支面向属性概念格，其时间复杂度会随形式背景(

G

,

M

,

I

)的面向属性概念格及其补背景概念格个数的变化而变化。若取

n

=max(||

L

(

G

,

M

,

I

)||，||

L

(

G

,

M

,

I

)||)，则该算法的时间复杂度为

O

(

n

)。总的来说，在已知形式背景(

G

,

M

,

I

)的情况下，求由属性诱导的三支面向属性概念格，利用本文算法可分成两个部分：利用相关知识求出形式背景(

G

,

M

,

I

)的

L

(

G

,

M

,

I

)和

L

(

G

,

M

,

I

)，按照文献[4]和通用的面向对象概念格构造算法，其时间复杂度为

O

(2+ 2)；在第一部分的基础上结合本文算法求出

L

(

G

,

M

,

I

)，其时间复杂为

O

(

n

+ 2+ 2)。基于文献[4]提出的基于背景叠置的三支面向属性格的构造算法，首先利用形式背景(

G

,

M

,

I

)和其补形式背景(

G

,

M

,

I

)构造一个混合形式背景，混合形式背景的对象个数为原形式背景(

G

,

M

,

I

)对象个数乘以2；然后求出混合形式背景的面向属性概念格，利用同构关系求出三支面向属性概念格。混合形式背景的对象个数多于原形式背景(

G

,

M

,

I

)的对象个数，按照文献[4]和通用的面向对象概念格构造算法，其时间复杂度为

O

(2+ 2)，通常情况下

O

(

n

+ 2+ 2)<

O

(2+ 2)，故本文算法比文献[4]算法的时间效率高。

4 结 论

定义极大和极小概念以及极大概念集和极小概念集，推导出由属性诱导的三支面向属性概念格、极大概念集和极小概念集三者之间关系，通过三者之间的关系求出由属性诱导的三支面向属性概念格；构造由属性诱导的三支面向属性概念格的生成算法，比较分析通用面向对象概念格构造算法与本文算法的时间复杂度。结果表明，通用面向对象概念格构造算法的时间复杂度为

O

(

n

+ 2+ 2)，本文算法的时间复杂度为

O

(2+ 2)，通常情况下

O

(

n

+ 2+ 2)<

O

(2+ 2)，本文算法的时间效率高于通用面向对象概念格构造算法。