基于改进线性Bregman算法的ECT图像重建算法

马 敏，孙美娟

(中国民航大学 电子信息与自动化学院，天津 300300)

1 引 言

电学层析成像(electrical tomography，ET)是20世纪80年代被提出并逐渐发展起来的一种多相流检测技术。它根据研究不同的电学特性，划分为电容层析成像(electrical capacitance tomography，ECT)、电阻层析成像(electrical resistance tomography，ERT)和电磁层析成像(electromagnetic tomography，EMT)。其中，电容层析成像因其在检测过程中具有非侵入性、无害性、成像速度快等特点，应用前景十分广泛[1]。目前主要应用于实时监测多相流的流型、工业管道内流体情况及航空器中的滑油等[2]。

电容层析成像主要包括传感器阵列、数据采集单元和图像重建三部分[3]。图像重建作为ECT系统的主要组成部分，其重建速度和质量对整个系统有着重要影响。目前ECT图像重建算法可分为非迭代类算法和迭代类算法。非迭代类算法主要有线性反投影，Tikhonov正则化、奇异值分解法(singular value decomposition，SVD)等，其共同点是一步成像，图像重建速度快，但重建精度不高。迭代算法主要有Landweber、共轭梯度(conjugate gradient，CG)等，其重建图像分辨率较好，但收敛速度较慢，实时性不佳。

Donoho和其他人引入了Bregman迭代并应用于解决基追踪问题[4,5]。由Osher S，Burger M，Goldfarb D，Xu J，Yin W等给出的线性Bregman迭代算法(linearized Bregman algorithm，LBA)主要用来求解稀疏问题，应用于图像去噪领域，之后又被用于基于压缩感知的图像重建问题，是一种快速、有效的优化算法。

本文将线性Bregman迭代应用到ECT图像重建当中，为进一步提高成像质量，减少成像时间，提出两种改进线性Bregman算法(modifified linearized Bregman algorithm，MLBA)，即通过奇异值分解和牛顿二阶迭代逼近广义逆，与线性Bregman迭代结合形成的两种混合迭代算法。然后利用图像重建速度、相对误差、相关系数等评价指标对常用的成像算法成像结果与改进后的算法成像结果进行对比分析。

2 ECT系统模型

电容层析成像基本工作原理是通过安装在被测管道外侧的敏感电容传感器，对管道内部介质进行测试并获取相应的介质信息，再借助于计算机图像重建算法，获取管道内介质分布图像。在实际操作过程中，由于不同流体的介电常数不同，当流体通过传感器阵列时会引起极板间介电常数的改变，从而引起电容值的变化，采集单元进行电容值数据采集，然后将数据处理后传送到成像计算机，成像计算机再选择合适的成像算法完成图像重建[6]。其系统模型如图1所示。

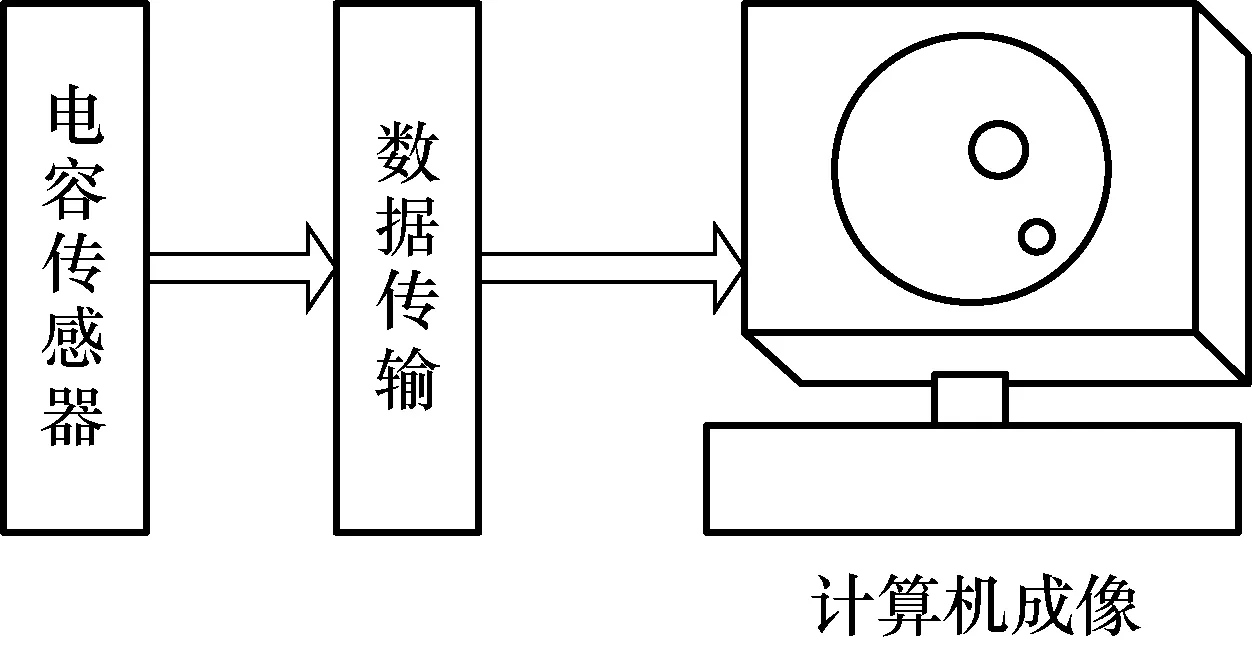
图1 ECT系统模型Fig.1 System model of ECT

ECT系统图像重建的线性模型如下：

SG=C

式中：C为M×1维的归一化电容测量值矩阵；G为N×1维的归一化介电常数分布矩阵，在图像重建过程中代表图像灰度值；S为M×N维矩阵，反映了电容C受物质分布变化G的影响，称为敏感场。

影响图像重建的主要因素有：(1)软场特性：敏感场分布易受被测介质分布的影响；(2)欠定性：反问题求解过程中，独立测量的电容值个数远小于未知量的个数，导致解不唯一；(3)不适定性：边界测量的变化对场域内介质变化不敏感，边界电位值的微小变化会引起解的较大变化，导致求解过程不稳定[7]。

在实际工程中，ECT技术中的非线性问题一般采用局部线性化的方法解决，因此，它的图像重建问题转变为一种优化问题。由于数据采集条件的限制，往往导致所采集的数据量不能满足恢复原始图像的要求，此时相应的重建方程SG=C就变成了一组欠定方程[8]。

3 线性Bregman迭代算法

在所有解决欠定线性系统Au=f的方案中，通过最小化l1范数‖u‖1来恢复u，这个问题被称为最小化问题：

(1)

线性Bregman算法在解决了Bregman每一步需要最小化的问题，实质上是一阶导数的线性逼近[9]。因此，非常适用于求解l1范数正则化问题，也符合ECT图像重建的求解问题。

3.1 线性Bregman迭代

定义3.1(Bregman距离)：凸函数J在u，v两点的Bregman距离D(u,v)定义如下：

式中：p∈∂J(v)是凸函数J在V点的次梯度。

利用Bregman距离的概念，线性Bregman迭代旨在解决式(1)中的优化问题:

(2)

式中：J(u)=‖u‖1；δ是常量；p0=u0=0。

由式(2)产生的序列{uk}k∈N的极限是式(3)的唯一解：

(3)

尽管式(3)与式(1)不同，但是当μ→∞时，式(3)趋近于式(1)，这个迭代方程可以写为如下形式：

(4)

这里u0=v0=0，软阈值算子

Tλ(w)=[tλ(w1),tλ(w2),…,tλ(wn)]T

(5)

式中：

(6)

在此基础上，把迭代规则式(4)推广到式(7)

(7)

式中：A∈Cm×n,m≤n，是任意矩阵，0<δ<2/‖AAT‖[10]。

且文献[10]中证明了当μ→∞，0<δ<1时，式(7)中序列极限趋向于式(1)的解，并且在所有解中最接近Au=f的最小l2范数解。

4 基于MLBA的ECT图像重建算法

尽管线性Bregman可以解决式(1)问题，但是由于线性Bregman的收敛速度与矩阵A的条件数有关，条件数越小，其收敛速度越快；式(7)中涉及求解A的广义逆矩阵，目前MATLAB中存在很多通过迭代方式逼近广义逆的方法[11]，但大部分都是一阶迭代，其收敛速度不快且误差较大。对此，本文通过减小A的条件数、提高求A+的迭代阶数来改进线性Bregman算法。

4.1 基于奇异值分解的线性Bregman重建算法

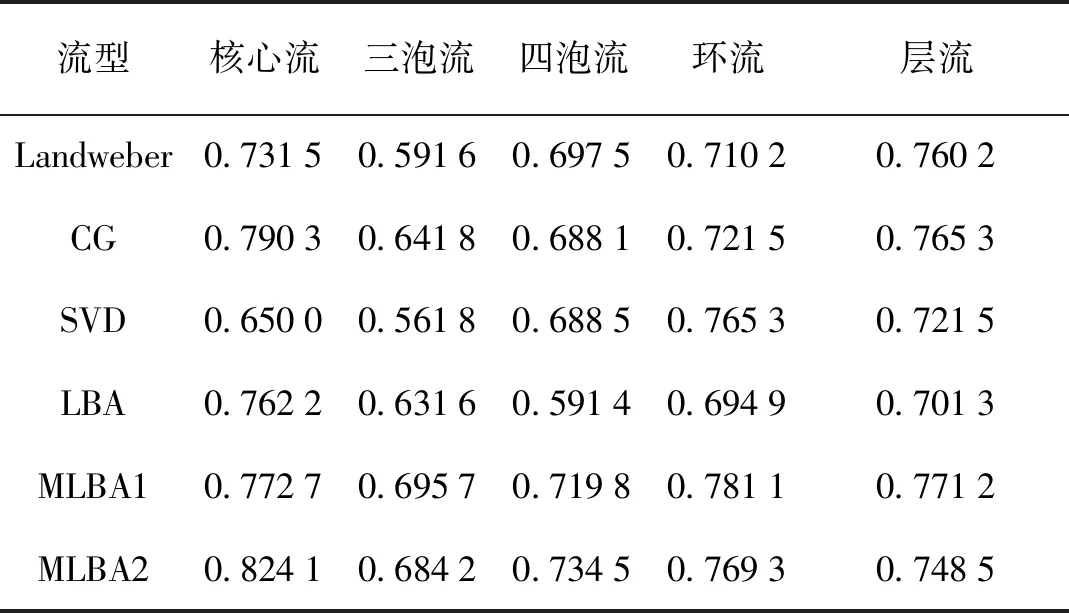
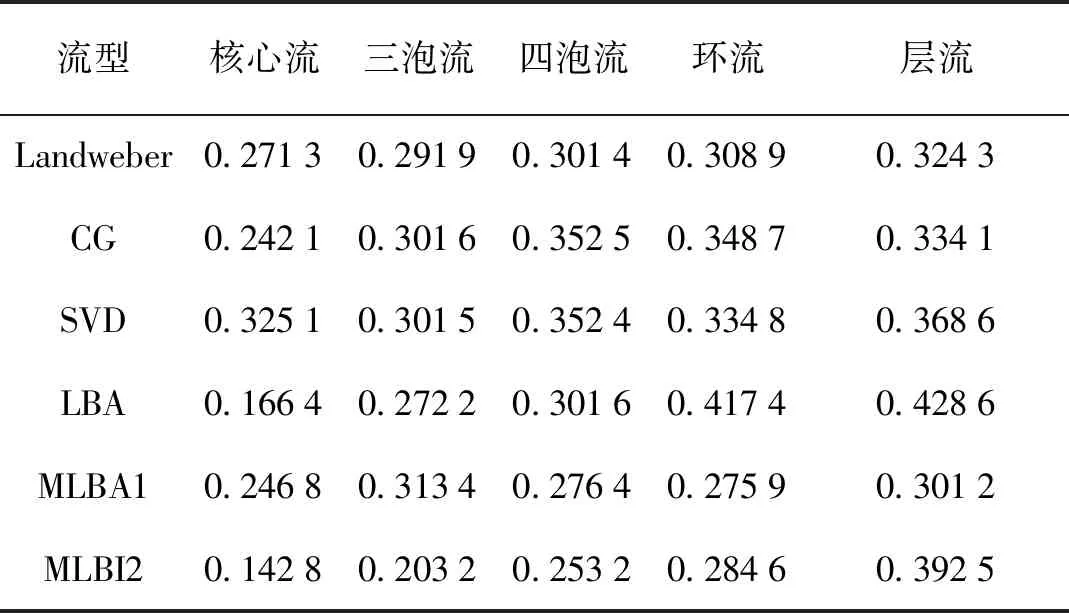
定义4.1(奇异值分解)：对于m×n的矩阵A(m

A=UDVT

式中：U是m×m阶酋矩阵；V是n×n阶酋矩阵；D是m×n的半正定对角矩阵，它的前r列的对角线元素包含了S的r个奇异值，即为矩阵S的全部非零奇异值，分别记作σ1,σ2,…,σr(σ1≥σ2≥…≥σr>0)，其中r是矩阵S的秩，其对于矩阵的影响也随着数值递减相应地减弱，其余对角元素为0。另外，U的列向量是AAT的特征向量，V的列向量是ATA的列向量。所以，A+=VD-1UT。

虽然SVD分解可以减小A的条件数，加速线性Bregman算法收敛速度[12]，但SVD分解耗费时长较长，且ECT系统中灵敏度矩阵的奇异值逐渐趋向于零。对此，有学者提出在D-1的前r个主对角元素加入修正因子的方法来改善A+的稳定性[13]，本文用此SVD思想来改进线性Bregman迭代，从而达到既提高收敛速度，也增加稳定性的目的。形成的改进算法1(MLBA1)如下：

(8)

式中：u0=0；f0=0；0<σ<1；kmax=20；k=0,1,2,…。

4.2 基于二阶迭代的线性Bregman重建算法

引理4.1：设给定矩阵A∈Am×n≠0，初始矩阵V0∈An×m满足[14]

(1)V0∈μ(A*,A*)

(2)ρ(I-AV0)<1

式中：I为m×m单位矩阵；ρ(A)是矩阵A的谱半径。则(9)产生的序列{Vq}q∈N收敛于A+。

Vq+1=Vq+V0(I-AVq),q=0,1,…

(9)

由于逼近引理4.1中的广义逆是一阶迭代，令：

Wq+1=Wq+Wq(I-AWq),q=0,1,…

(10)

式中：W0可以是满足ρ(AW0-AA+)<1的任意矩阵，这里取W0=V0=αAT；迭代序列Vq和Wq之间的关系是Wq=V2q-1，从而把一阶迭代变为二阶迭代。

由文献[4]可知，‖A+-V2q-1‖≤‖A+-V0‖‖I-αAA*‖2q-1，又因为‖I-αAA*‖<1，所以‖A+-V2q-1‖<‖A+-V0‖。

因此，V2q-1比V0更接近A+，二阶迭代将比一阶迭代提供更多关于A+的信息，且迭代收敛速度增加，从而不仅能提高图像重建速度，也提升了重建质量。用二阶迭代改进线性Bregman迭代，形成改进算法2(MLBA2)如下：

(11)

式中：u0=0；ξ0=Wqf0；f0=0，0<δ<1；0<α<1/‖A‖2；W0=αAT。基于MLBA2的求解步骤如下：

1)初始化：

k=0，u0=0，ξ0=Wqf0，f0=0，α=1/2‖A‖2，δ=0.3，kmax=100，W0=αAT，ε=0.18，μ=0.5

2)先计算Wq：

Wq+1=Wq(2I-AWq),q=0,1,2

3)执行步骤4～7，直到满足停止标准。

4)计算：fk+1=fk+(f-Auk)。

5)计算：ξk+1=ξk+Wq(fk+1-Aξk)。

6)计算：uk+1=δTμ(ξk+1)

7)如果满足任何一个停止迭代标准，则迭代停止。

相对误差：‖uk+1-uk‖/‖uk‖<ε

绝对误差：‖uk+1-uk‖<ε

最大迭代次数：k=kmax

8)返回输出uk+1。

5 仿真及结果分析

为验证本文提出的两种MLBA算法图像重构效果，实验选取12电机的仿真模型，管道外径50 mm、内径46 mm，对气固两相流进行建模分析，各类介质介电常数分别取：空气1,铜2.2,塑料5.8,玻璃4.2。

依次对核心流、三泡流、四泡流、环流和层流5种流型进行仿真，仿真原型见表1中第1行所示。使用COMSOL Multiphysics 5.3软件建立模型，采用网格自动剖分法，对正问题进行求解；然后通过Matlab 2016a对反问题求解，进行图像重建仿真实验。实验选取Landweber、CG、SVD、线性Bregman迭代算法与MLBA算法进行仿真对比，各个参数取值为：q=2[15]，μ=5[16]，δ=0.3，kmax=100，ε=18，μ=0.5图像评价标准采用图像重建速度、相关系数和相关误差[17]。

各种算法图像重建效果如表1所示，图像重建速度如表2所示，相关系数和相对误差如表3、表4所示。

由表1图像可知，LBA可以用于ECT图像重建，但仅在核心流中成像效果好，对其他复杂流型成像效果很差。MLBA1和MLBA2算法在成像质量上相对于Landweber、CG、SVD、LBA算法有明显提升，其中，核心流的伪影得到改善；三泡流和四泡流减少了图像粘连情况，目标位置、轮廓较为清晰；环流不仅形状得到改善，而且伪影减少。且MLBA1相比MLBA2算法图像伪影更小，成像更清晰。虽然MLBA1成像效果最好，但由表2可知，MLBA1在时间上相比Landweber、CG、SVD并无很大优势，且图像越复杂比其他算法耗费时间越多。而MLBA2算法，在成像速度上有很大提升，只需Landweber算法成像时间的近十分之一，MLBA1成像时间的约20分之一。因此从系统实时性和重建质量两方面综合考虑，MLBA2算法的优势更明显。

表1 不同算法重建效果Tab.1 Reconstruction effects of different algorithm

表2 图像重建速度比较Tab.2 Comparison of image reconstruction speed s

从表3和表4的误差指标数据可知，MLBA1与MLBA2的图像误差得到了很好的控制，图像相对系数也相对得到了提高。故改进后的算法提高了图像成像质量。

表3 图像相关系数Tab.3 Comparison of image correlation coefficient

表4 图像相对误差Tab.4 Comparison of image relative error

6 结 论

本文在分析ECT欠定性问题的基础上，将线性Bregman迭代算法应用到ECT图像重建过程，并对该算法进行了改进，使之不仅具有线性Bregman算法的优点，而且可以加快计算速度，提高准确性。仿真实验表明，基于线性Bregman迭代算法能够实现ECT图像的重构，但对复杂流型成像质量不高。本文提出的两种改进算法，相比Landwebr、CG、SVD、线性Bregman算法，具有更好的图像分辨率和更快的成像速度。但是，由于仿真的流型有限且线性Bregman迭代中涉及广义逆矩阵的求解，后续研究可以继续优化广义逆的求解方法，使该算法在电容层析成像技术中更有优势、效果更佳。