悬挂穿孔法测试织物弯曲悬垂性

陈文苗 刘成霞

摘要： 为探究同时测试织物弯曲性和悬垂性的方法，文章以24块常见机织物为研究对象，分别用斜面悬臂梁法和圆台法测试抗弯刚度和悬垂系数，之后自行设计悬挂穿孔法测试装置并进行实验，提取得到四项特征指标：侧轮廓面积、底轮廓面积、载荷峰差值、峰值膨胀角。相关分析和回归分析的结果表明：悬挂穿孔法可以同时测量织物弯曲性和悬垂性，且四项特征指标都与抗弯刚度、悬垂系数具有高度相关性，得到的两个回归方程可用于预测织物整体的抗弯刚度和悬垂系数。悬挂穿孔法只用一块试样就能综合表达织物整体的弯曲悬垂性，既节约测试时间，又节省测试面料。

关键词： 织物;弯曲性悬垂性;抗弯刚度;悬垂系数;悬挂穿孔法

中图分类号： TS101.923

文献标志码： A

文章编号： 10017003（2021）08004007

引用页码： 081108

DOI： 10.3969/j.issn.1001-7003.2021.08.008（篇序）

Measurement of fabric bending and draping properties by hanging & perforating method

CHEN Wenmiaoa， LIU Chengxiaa，b，c

（a.School of Fashion Design & Engineering; b.Zhejiang Province Engineering Laboratory of Clothing Digital Technology;c.Key Laboratory of Silk Culture Heritage and Products Design Digital Technology， Ministry of Culture and Tourism，Zhejiang Sci-Tech University， Hangzhou 310018， China）

Abstract： To investigate fabric bending and draping properties， as well as relevant measurement methods， 24 common woven fabric were selected as the research object. Then， the bending rigidity and draping coefficient were tested using method of cantilever beam on bevel and circular table. Next， a hanging & perforating testing device was designed for the experiment. As a result， four indexes were extracted： lateral outline area， bottom outline basal area， the difference of load peak value with original value， the flare angle with a peak value. Results of correlation analysis and regression analysis indicate that hanging & perforating method can be used to test fabric bending and draping properties simultaneously. And the four indexes are highly correlated with bending rigidity and draping coefficient. Finally， two regression equations obtained can be used to predict the fabric overall bending rigidity and draping coefficient. The hanging & perforating method can comprehensively reflect fabric overall bending and draping properties only by means of a fabric sample. It can save both the testing time and the testing fabric.

Key words： fabric; bending & draping properties; bending rigidity; draping coefficient; hanging & perforating method

收稿日期： 20210301;

修回日期： 20210712

基金項目： 浙江省自然科学基金项目（LY20E050017）

作者简介： 陈文苗（1996），女，硕士研究生，研究方向为纺织服装检测技术。通信作者：刘成霞，教授，glorior_liu@163.com。

弯曲性和悬垂性是影响和决定织物外观、风格的重要属性，其测试方法一直受到纺织学者的广泛关注[1]。目前最常用的方法是斜面悬臂梁法测弯曲性和圆台法测悬垂性，近年来众多科技工作者利用新科技与新装置探究和优化织物弯曲性、悬垂性的测试方法，如利用织物弯曲形态曲线[2]、水滴法[3]及KES-FB型织物风格仪[4]测试织物弯曲性;运用3D扫描技术[5]、三维形态立体测试法[6]及结合神经网络深度学习[7]测织物悬垂性等。这些方法虽然对弯曲、悬垂性的测试进行了创新，测试精度和效率比传统方法有了较大提升，但织物弯曲性和悬垂性的测试[8]一直都是分开进行的，且一块试样只能测试织物某一方向的弯曲性[9]。而织物具有明显的各向异性，要想得到织物多方向的弯曲性[10]，需要裁剪多块试样进行多次测试，不仅费时费力，还要耗费大量原材料，尤其对于高档试样来说，成本耗费较大。

实际上弯曲性和悬垂性是相互影响、密切关联的，容易弯曲的织物一般有较好的悬垂性;悬垂性差的织物也不易弯曲，比较硬挺，如能将其合二为一，则将大大节约测试时间和成本。针对这一现状，本文尝试探索一种能同时测量织物整体弯曲性和悬垂性的方法。

1 实 验

1.1 试样的选取与仪器

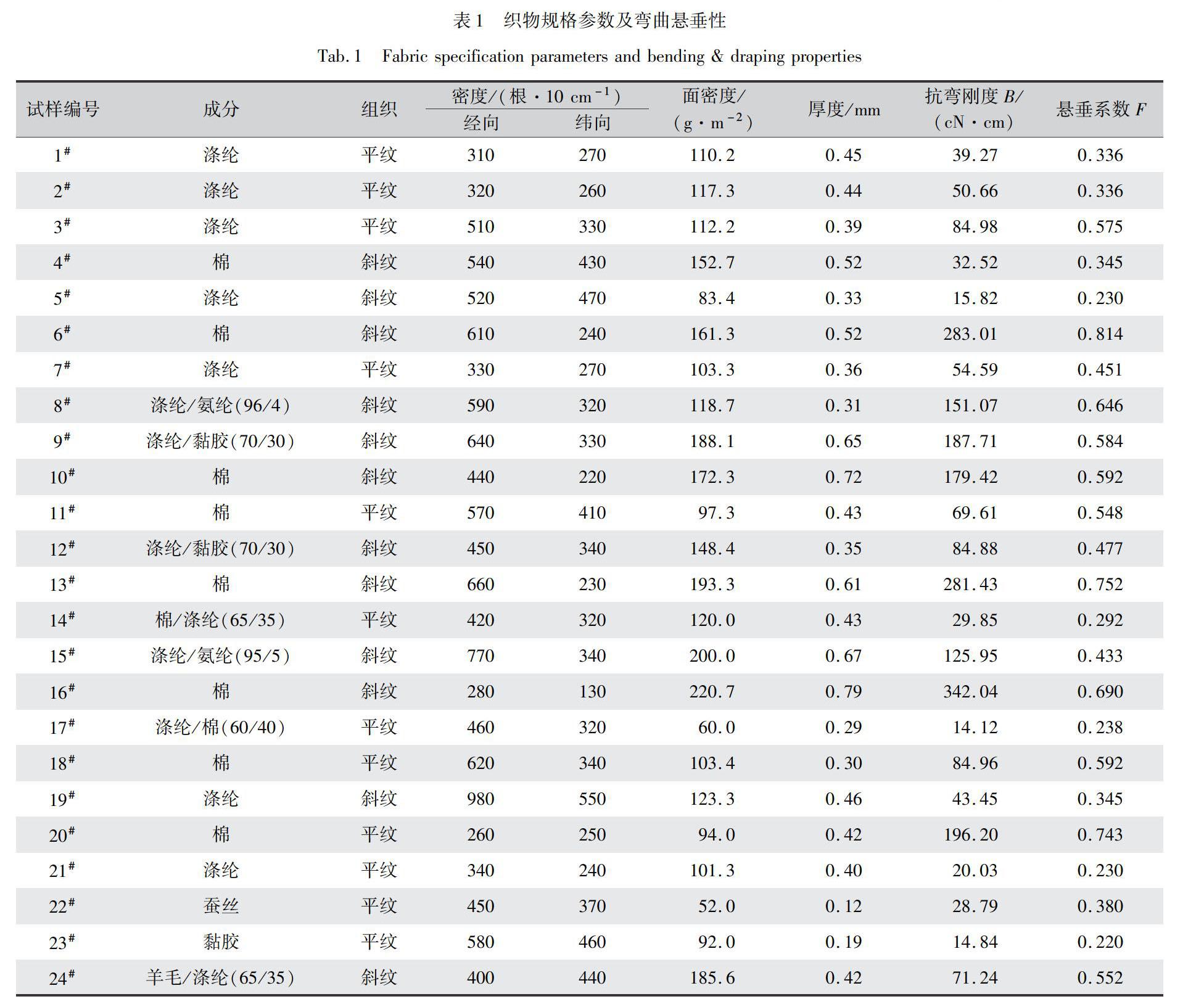
选取弯曲性和悬垂性差别较大的常见机织物共24种，规格参数如表1所示。

所需仪器：YG（B）022D型自动织物硬挺度试验仪（温州际高检测仪器有限公司），YG811型织物悬垂性测定仪（武汉国量仪器有限公司），INSTRON3367型双立柱台式电子试验机（英斯特朗公司），佳能700D相机（市售）。

1.2 测试织物弯曲性和悬垂性

根据GB/T 18318—2001《纺织品织物弯曲长度的测定》，用YG（B）022D型自动织物硬挺度试验仪测试织物经向（0°）、纬向（90°）、45°、135°四个方向（每个方向5块试样求平均值）的抗弯刚度，并计算平均抗弯刚度B（cN·cm）作为最终结果;根据GB/T 23329—2009《纺织品织物悬垂性的测定》，用YG811型织物悬垂性测定仪测试悬垂系数F。所有测试均在恒温恒湿的标准大气环境中进行，结果如表1所示。

1.3 悬挂穿孔法测试织物弯曲悬垂性

1.3.1 测试装置及原理

实验装置由提升杆（其下端设有直径3 cm的小圆台）、圆孔盖（外圆直径24 cm和内圆直径5 cm的圆环形）、无孔盖（直径24 cm）、外筒壁（直径24 cm）组成，如图1（a）所示。圆孔盖的孔径是经过多次预实验后确定的，研究发现直径5 cm最合理，孔径过小会导致织物穿孔过程中受摩擦力影响过大，提拉所需的载荷值与织物的弯曲悬垂性相关性较差，实验结果不理想;而孔径过大会使一些较柔软、极易悬垂的织物穿孔时过于轻松，提拉所需的载荷峰值非常不明显，实验结果也不理想。圆孔直径在5 cm左右时，穿孔提拉时的载荷峰值较明显，且比较稳定。

使织物在提升杆的小圆台上悬挂并自然下垂，弯曲悬垂性不同的织物形成的形状也不相同，即通过静态悬挂形状来表征织物弯曲悬垂性;然后将带有织物的提升杆从圆孔盖的中空圆心匀速穿出，弯曲悬垂性不同的织物在穿孔过程中的

形变和拉力不同，即通过形变和拉力来表征织物弯曲悬垂性，故将其命名为“悬挂穿孔法”。

经研究发现，在提升杆上静态悬挂下的圆形试样侧截面和底截面各不相同，抗弯刚度和悬垂系数越大的织物，形成的侧面和底面面积越大;抗弯刚度、悬垂系数越接近的织物，侧面和底面的轮廓形状、张开角度也非常相似;而在匀速提升织物穿孔的过程中，抗弯刚度和悬垂系数越大的织物，提升所需的拉力也越大，且抗弯刚度和悬垂系数不同的织物，拉力达到峰值时织物收缩形成的轮廓和夹角也不相同，而抗弯刚度和悬垂系数越接近的织物，这些数值也越接近。

1.3.2 实验准备

1）实验工具：自制图1（a）所示的装置，佳能700D相机，支架，INSTRON3367型双立柱台式电子试验机。

2）实验试样：将织物熨烫平整，并裁剪成直径24 cm的圆形，正中心剪出直径1 cm的圆孔（用来穿过提升杆）。

3）测试条件：恒温恒湿的标准大气环境，室内光照均匀且充足，在测试前已将试样在此条件下进行调湿24 h。

1.3.3 实验流程

步骤（1）：将织物中心圆孔穿过提升杆，置于小圆台上而自然下垂，使提升杆固定在无孔盖中心，如图1（b）所示。

步骤（2）：将相机固定在支架上，分别在外筒壁四周等距离处和外筒壁正下方，拍摄织物自然下垂后的形状。得到试样的5张静态照片（包括4张侧面图和1张底面图）。

步骤（3）：取下无孔盖，换上圆孔盖，使提升杆从圆孔盖中穿出，固定在INSTRON3367型双立柱台式电子试验机的上夹板中，如图1（c）所示。试验機的提拉速度为15 mm/min。

步骤（4）：用相机从侧面录制步骤（3）中织物形变视频，即记录提升杆在试验机拉伸力的作用下将试样从圆孔中缓慢向上提拉，直至被完全抽出，随后恢复自然下垂形态的整个形变过程。由试验机可得到时间（s）-载荷（N）的关系曲线。步骤（4）与步骤（3）同时进行。

步骤（5）：利用视频处理软件，截取织物从圆孔盖抽出前的时刻，将其定义为初始时刻（0 s），得到试样从0～142 s的载荷及形变曲线。

1.3.4 特征值选取

如前所述，弯曲性及悬垂性不同的织物自由下垂形成的形状轮廓、向上提升时的载荷及形变均不同，因此引入侧轮廓面积、底轮廓面积、载荷峰差值、峰值膨胀角作为织物截面特征值。

1）侧轮廓面积S：织物悬挂自由下垂时形成的4个侧面轮廓面积S1、S2、S3、S4的平均值;

2）底轮廓面积S0：织物悬挂自由下垂时形成的底面轮廓面积;

3）载荷峰差值f1、f2、f3：时间-载荷曲线中的3个载荷峰值与未启动拉伸时的载荷值之差;

4）峰值膨胀角θ：时间-载荷曲线中，峰值时刻的织物两条边缘形成的夹角。两条边缘指的是视频中截取峰值时刻的图片，此时图中所能看到的织物以提升杆为顶点张开的最大角的边缘。

研究发现：织物时间-载荷曲线存在3个峰值，第一个峰值最明显，此时的膨胀角随织物的弯曲悬垂性不同而变化更大，所以峰值膨胀角以第一峰值时刻为准。

2 结果与分析

2.1 悬挂穿孔法所得测试结果

表2列出了利用本文提出的悬挂穿孔法测试时的各项指标参数。

将表2中24种织物的第一载荷峰值f1从小到大排列，依次为：17#、23#、5#、21#、19#、22#、14#、1#、4#、2#、7#、3#、12#、15#、18#、9#、11#、24#、10#、8#、20#、13#、16#、6#。按此顺序做抗弯刚度、悬垂系数随第一载荷峰值增大的折线图，图2（a）（b）中横坐标均为按第一载荷峰值从小到大的排序，即横坐标的1～24分别对应17#、23#、5#……16#、6#织物，作为编号排序。图2显示，随着第一载荷峰值的增大，抗弯刚度和悬垂系数也呈增长趋势，表明第一载荷峰值f1与抗弯刚度B、悬垂系数F具有较明显的相关性。

2.2 悬挂穿孔法的时间-载荷曲线

经研究发现，24种织物的时间-载荷曲线中都具有3个明显的载荷峰值，由于篇幅有限，本文从中选出4个较有代表性的织物（3#、9#、10#、13#），其时间-载荷曲线如图3所示。

从图3可以看出，不同织物的第一载荷峰值f1差别较明显，4种织物按f1从小到大依次为3#、9#、10#、13#，其中9#和10#织物的f1非常接近。经对比发现，3#织物的B（84.98 cN·cm）和F（0575）都较小，9#、10#织物的B（187.71、179.42 cN·cm）和F（0584、0.592）稍大且十分接近，13#织物的B（281.43 cN·cm）和F（0.752）都较大，即弯曲性、悬垂性越好的织物，穿孔过程中第一次峰值时的载荷越小，与2.1相吻合。究其原因，越易弯曲、悬垂性越好的织物，悬挂自然下垂形成的夹角越小，因而更容易穿过圆孔，即所需拉力越小，故f1较小。在后续数据处理中会进一步分析探究f2和f3与织物弯曲性和悬垂性的关系。

2.3 悬挂穿孔法所得指标与抗弯刚度、悬垂系数之间的相关性分析

为进一步明确利用本文提出的新指标是否与传统指标具有统计学意义上的相关性，对4个新指标与抗弯刚度B和悬垂系数F之间进行pearson相关性分析，相关系数如表3所示。

从表3可看出，悬挂穿孔法中的侧轮廓面积S、底轮廓面积S0、载荷峰差值f1、f2、f3、峰值膨胀角θ都与抗弯刚度B和悬垂系数F呈显著正相关关系。即B和F越大的织物，用悬挂穿孔法所得的4项新指标也越大，可以解释为：越硬挺的面料，自然悬挂时越不易弯曲和下垂，张开的轮廓和角度越大，提升时穿过圆孔所受的摩擦阻力就越大，即越不易穿过圆孔，所以提拉织物需要的力（即载荷）就越大。3个载荷峰差值与B、F的相关性从大到小依次是f1、f3、f2，因此仅选择f1代表载荷峰差值。与B相关性从大到小依次是载荷峰差值f1、底轮廓面积S0、侧轮廓面积S、峰值膨胀角θ;与F相关性从大到小依次是侧轮廓面积S、峰值膨胀角θ、底轮廓面积S0、载荷峰差值f1。

2.4 单一新指标与弯曲性及悬垂性之间的关系

为进一步建立新方法中的4个特征参数（即f1、S0、S和θ）与传统方法中的抗弯刚度B及悬垂系数F之间具体的关系式，将4个新指标与2个传统指标之间进行曲线拟合，所得结果如图4、图5所示。

图4和图5显示，4个新指标与抗弯刚度、悬垂系数呈幂函数或线性关系，与抗弯刚度拟合优度从高到低依次是f1、θ、S0、S，与悬垂系数的拟合优度从高到底依次是f1、S、S0、θ。虽然每个新指标均与抗弯刚度、悬垂系数存在较密切的关系，但在运用这些关系式预测抗弯刚度和悬垂系数时不是非常方便。

2.5 新指标与抗弯刚度及悬垂系数的综合关系式

2.5.1 抗弯刚度的预测方程

运用多元逐步回归进一步探究悬挂穿孔法中的4个新指标与抗弯刚度B的关系，最终得到包含载荷峰差值f1和峰值膨胀角θ的回归方程：

B=129.253f1+1.649θ-56.613（1）

式（1）通过了F检验，拟合优度为0.901。f1与θ的回归系数均小于0.05，即通过了t检验，所以该方程能用来预测抗弯刚度B。

2.5.2 悬垂系数的预测方程

用与2.5.1同样的方法，得到了包含侧轮廓面积S、底轮廓面积S0的回归方程：

F=0.584S+0.224S0-0.264（2）

经检验，式（2）也通过了F检验和t检验，拟合优度为0.851。

综合以上分析，利用悬挂穿孔法可以实现织物弯曲性和悬垂性的表征，本文提出的侧轮廓面积、底轮廓面积、载荷峰差值、峰值膨胀角特征指标与抗弯刚度及悬垂系数都存在密切的关系，且構建了可以利用新指标预测抗弯刚度和悬垂系数的方程，实现织物抗弯刚度与悬垂系数的二合一测试，能较为高效地表达织物多个方向综合的弯曲性和悬垂性。

3 结 论

以24块试样为研究对象，利用自行设计的实验装置，结合INSTRON3367型双立柱台式电子试验机对织物进行测试，提取了侧轮廓面积S、底面轮廓面积S0、载荷峰差值f1、峰值膨胀角θ这4个特征指标，经研究得到以下结论。

1）悬挂穿孔法中的4项特征指标与斜面悬臂梁法中的抗弯刚度、圆台法中的悬垂系数都具有高度正相关关系，表明利用本文提出的悬挂穿孔法测试织物弯曲性和悬垂性具有一定的可行性。

2）与斜面悬臂梁法中的抗弯刚度相关性从大到小依次是f1、S0、S、θ;与圆台法中的悬垂系数相关性从大到小依次是S、θ、S0、f1。

3）利用悬挂穿孔法中的侧轮廓面积S、底轮廓面积S0、载荷峰差值f1和峰值膨胀角θ，可以同时实现对织物抗弯刚度B和悬垂系数F的预测。

4）悬挂穿孔法只需一块圆形试样就可测得织物多方向综合的弯曲性，且能实现弯曲性和悬垂性的二合一，有助于节约测试时间和测试原料。

悬挂穿孔法不同于另一种织物风格测试仪PhabrOmeter的地方是：PhabrOmeter对于穿孔过程的记录仅仅是载荷-位移变化，而悬挂穿孔法除了记录拉力（即载荷变化），还能定点拍摄穿孔全过程，记录织物试样的形状变化，可在曲线图上找到任意时刻（从视频中截取该时刻）的织物形状，进而提取形状变化特征值，即可多方面、更准确地表征织物形变时的弯曲悬垂性。

参考文献：

[1]朱婉萍， 范雪荣， 高卫东， 等. 基于PhabrOmeter对不同整理纯棉织物风格的评价[J]. 印染， 2021， 47（1）： 11-14.

ZHU Wanping， FAN Xuerong， GAO Weidong， et al. Evaluation of the style of different finished cotton fabrics based on PhabrOmeter[J]. China Dyeing & Finishing， 2021， 47（1）： 11-14.

[2]余芳， 刘成霞. 用蝴蝶结法测试毛织物弯曲性[J]. 纺织学报， 2019， 40（8）： 35-39.

YU Fang， LIU Chengxia. Measurement for bending behavior by bowknot method[J]. Journal of Textile Research， 2019， 40（8）： 35-39.

[3]刘成霞， 韩永华， 张才前. 基于图像处理的织物弯曲性能测试方法[J]. 纺织学报， 2013， 34（7）： 52-56.

LIU Chengxia， HAN Yonghua， ZHANG Caiqian. Test method for fabric bending behavior based on image processing[J]. Journal of Textile Research， 2013， 34（7）： 52-56.

[4]PARK H Y， BAEK Y M， AN S K. Effects of mercerization and plasma pretreatments on the mechanical properties and flame retardancy of flame-retardant cotton fabrics[J]. Textile Science and Engineering， 2018， 55（5）： 295-303.

[5]王鹏程， 刘基宏. 基于3D扫描技术的织物悬垂性测试方法[J]. 丝绸， 2018， 55（6）： 25-30.

WANG Pengcheng， LIU Jihong. Method of fabric drape test based on 3D scanning technology[J]. Journal of Silk， 2018， 55（6）： 25-30.

[6]韩剑虹， 周衡书， 武世锋， 等. 基于三维人体形态的织物立体悬垂測试方法与表征[J]. 纺织学报， 2018， 39（1）： 39-44.

HAN Jianhong， ZHOU Hengshu， WU Shifeng， et al. Text method and characterization of 3D drape for fabrics based on human body form[J]. Journal of Textile Research， 2018， 39（1）： 39-44.

[7]余志才. 基于三维模型和深度学习的织物悬垂性能研究[D]. 上海： 东华大学， 2020.

YU Zhicai. A study on Fabric Drape Based on Three-Dimnesional Model and Deep Learning[D]. Shanghai： Donghua University， 2020.

[8]孙丰鑫. 基于纺织品风格仪的机织物多重性能及硬挺度的建模与表征[D]. 上海： 东华大学， 2017.

SUN Fengxin. Modelling and Characterization of Multiple Physical Properties and The Stiffness Handle of Woven Fabrics Based on the CHES-FY System[D]. Shanghai： Donghua University， 2017.

[9]刘成霞， 周澳. 利用十字交叉法测试织物弯曲悬垂性[J]. 纺织学报， 2018， 39（6）： 42-46.

LIU Chengxia， ZHOU Ao. Measurement of fabric bending and draping properties using crossing method[J]. Journal of Textile Research， 2018， 39（6）： 42-46.

[10]FARAJIKHAH S， MADANIPOUR K， SAHARKHIZ S， et al. Shadow moire aided 3-D reconstruction of fabric drape[J]. Fibers and Polymers， 2012， 13（7）： 928-935.