基于机器学习策略的半潜式钻井平台结构设计优化
2021-09-06周佳,孙伟,陈婕,王璞
周 佳,孙 伟,陈 婕,王 璞
(1.中国船舶及海洋工程设计研究院 海工部,上海 200023;2.诺易思工程软件(上海)有限公司,上海 200041)
0 引 言
随着海洋油气开发由浅水走向深水,超深水钻井平台的开发需求也应运而生,受海洋工程装备建造中常用钢结构材料级别和焊接工艺的限制,为达到更高技术指标,对结构设计提出更精准、更优化、更轻量化等方面的要求。近年来,国内已在海洋工程结构设计技术上取得长足进步,掌握了独立设计开发的技术能力。然而与国外设计公司相比,在结构强度分析精度、结构总强度快速评估、关键连接节点型式设计和方案累积等方面还存在一定的差距,仍需开展深入研究。
传统结构设计往往仅以满足结构强度要求为唯一目的,通常以母型船为参考,结合一定的专家经验和工程要求进行设计微调,在有限的几个方案中比选得到较优的设计方案。机器学习是关于理解与研究学习的内在机制、建立能够通过学习自动提高自身水平的计算机程序的理论方法的学科。近年来,机器学习理论在诸多应用领域得到成功应用与发展,已成为计算机科学的基础及热点之一。计算机能力的发展和优化算法的不断更新使得采用机器学习策略对结构设计进行优化,在满足结构强度与结构钢料轻量化之间寻找最佳平衡点成为可能。
本研究采用数值优化分析方法,基于机器学习优化算法相关理论,在数值优化分析平台上搭建结构优化分析工作流。在此基础上,进一步对优化工作流过程中结构分析各个步骤开展程序化、参数化描述方法的探讨,实现从定性手动试算优化到定量自动迭代优化的技术突破。通过分析输入、输出参数的相关性,对半潜式平台结构关键区域进行多目标优化分析和设计,得到优化方案帕累托解级和相关敏感设计参数,可供后续工程设计开发参考。
1 传统半潜式钻井平台结构设计方法
半潜式钻井平台主体结构主要由下浮体、立柱与上船体(或上部模块主框架)结构等3个部分组成,部分平台立柱之间设有横向或斜向撑杆。各部分自成一体,同时又相互连接,以抵抗不同设计状态下的自重、功能载荷和环境载荷。
与单体式船型浮体不同,半潜式平台总强度分析需要分别考虑静载、横向分离力、纵向剪切、扭矩、惯性加速度等多个主控载荷模式,以3个部分中保持连续关系的结构作为主要承载构件,保证结构顺利地将主甲板以上的各种功能载荷、水线以下结构承受的波浪载荷传递扩散至整个平台。因此,上述总强度载荷传递路径上的连接结构合理设计是平台结构安全的关键保证[1-3]。
由于半潜式平台的构造特点,其主要承载构件连接区域结构不可避免地存在形状突变,因而产生应力集中和疲劳问题[4]。为此,结构设计必须针对可能的疲劳热点对局部节点形状、构件尺寸进行详细的分析校核验证,通常采用更准确的细化有限元强度分析和谱疲劳分析方法校核以保证强度分析结果可信,相关指标满足规范和设计指标要求[5]。根据半潜式钻井平台的结构特点,关键区域结构设计流程如图1所示。

图1 关键区域结构设计优化分析流程
由图1可知:在设计初期较多依赖于设计参考母型;在设计中期会有大量同质性的计算分析和设计调整过程;在设计后期则需根据不同的生产实际需求对设计方案进行调整。尤其在设计中期,批量分析计算和调整涉及大量人力和资源,对于项目整体推进和控制非常不利,方案优化更是成本倍增。
2 关键区域结构优化机器学习策略应用
由于机器学习策略是基于大量样本数据的分析工作,在将机器学习策略应用于半潜式平台结构优化设计时,需对设计进行大量的参数研究工作,根据不同的设计参数,获得平台在关键区域的强度结果、疲劳结果等数据,建立设计参数与强度和疲劳的对应关系,并采用机器学习策略对数据进行分析,获得最优的平台设计方案。方案分析采用挪威船级社(DNV)的SESAM计算软件包完成。
优化过程用诺易思工程软件有限公司的Optimus软件建立计算分析工作流模板,将设计分析流程固化,实现设计参数自主调整和分析流程自主驱动,更易控制工作质量。可通过设置输入参数范围,简化建模工作量,大量节省人力成本。通过机器学习策略的应用,获得多组满足设计要求的方案和帕累托前沿,为设计优化缩小搜索范围,为最终方案提供多种选择。
2.1 优化工作流
优化工作流集成了在GeniE软件中建立结构关键区域的参数化高精度结构模型过程,根据设计校核要求,需分别对应强度指标和疲劳指标,评估结构在平台自存工况和作业工况下的响应。优化工作流还集成了通过HydroD和Submod完成模型的载荷映射过程。分析计算集成了Sestra分析模块,并可通过Xtract完成计算结果组合和提取,获得有限元网格中最大应力计算值进行强度评估。此外,通过集成Stofat完成模型疲劳评估,用同一个参数化的GeniE模型实现评估两个方向的多学科流程。由于SESAM软件包中各模块功能和调用方式差异较大,因此在工作流搭建中分别编制各模块调用接口代码、各模块模型分析驱动命令流自动生成子程序、结果组合及分析结果最大值搜索子程序、最大应力单元及相邻网格定位子程序等。优化工作流如图2所示。在工作流搭建完成后,进行单点试验计算验证,所得结果与常规设计人员驱动分析流程结果一致,实现批量化处理模型多目标分析的功能。

图2 优化工作流示例
2.2 关键结构设计输入和模型参数化
主要针对立柱与下浮体中纵连接肘板关键结构开展设计分析。对肘板模型进行参数化,研究不同肘板形式,得到设计参数对强度和疲劳指标的影响。肘板设计参数如表1所示,设计变量组合方案数量远超1010量级。

表1 肘板设计输入参数
为了更加直观和便于讨论,对不加肘板面板的结构形式进行介绍。为实现后续针对不同材料结构强度评估和疲劳热点插值分析代码生成需要,在参数化建模过程中通过分组定义肘板和相邻区域结构,部分位置如图3所示。
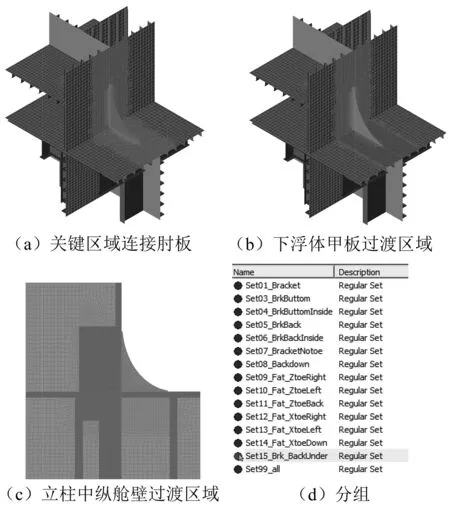
图3 参数化建模及分组
按照规范和设计要求,屈服强度分析和疲劳强度分析对分析模型的有限元网格要求不同。在参数化建模中,为兼顾两者,对模型采用疲劳分析模型t×t(t为板厚)的建模策略,在相应的屈服强度评估中采用对应的细化网格分析许用应力放大标准。
2.3 结构多工况分析载荷映射及计算分析
按照规范和设计要求,关键区域结构屈服强度和疲劳强度评估的控制工况分别为平台生存工况和作业工况。在参数化建模策略基础上,在载荷映射步骤中,通过HydroD和Submod对子结构进行波浪载荷的加载和整体模型载荷边界的映射,链接不同环境参数和不同平台装载设置下的总强度模型,提取子模型边界载荷。采用Sestra计算分析加载后不同设计方案子模型,即可得到不同方案下的应力分布,在计算结果基础上通过Stofat对疲劳热点进行应力插值,对应适用的S-N曲线,即可求得相应热点的疲劳寿命。
此外,根据肘板的臂长设计参数计算获得上下肘板趾端的两个疲劳热点位置坐标,采用二次开发程序找到定点位置周围分组中的单元,然后找出每个单元其周围的单元,进而获得0t(连接位置)、1/2t(1/2板厚处)和3/2t(3/2板厚处)处的坐标点,最终生成Stofat的执行脚本提交计算,评估这些热点位置的疲劳寿命。分析流程如图4所示。

图4 疲劳热点分析流程
在一定设计样本完成计算分析的基础上,用皮尔森相关性计算方法对结果进行分析,了解变量间的相关程度,求出变量间相关程度与变化方向的量数,即相关系数r:
(1)
式中:r位于区间[-1,1]内,越接近于零,相关性越小。
立柱与下浮体连接区域结构分析结果如表2所示。与质量正相关的设计变量是立柱中纵舱壁过渡板厚(thk_BrkBack)和下浮体中纵舱壁过渡板厚(thk_BrkBackInside)等,与疲劳年限相关的设计变量是肘板板厚(thk_bracket)和下浮体上甲板板厚(thk_Brkbuttom)等。质量与疲劳年限存在明显的相关关系,质量越大、疲劳损伤越小,即疲劳寿命越大,对于预定的质量更轻和疲劳寿命更长的优化目标即存在明显的优化方向冲突。另一方面,从疲劳优化目标参数与下浮体中纵舱壁过渡板厚的相关性曲线(见图5)也可发现,随着板厚增加质量相应增加,疲劳损伤反而变大,即疲劳寿命甚至会降低,这也说明质量与疲劳寿命并非简单的逆向冲突关系。因此,必须采用综合的多目标优化算法描述优化多目标参数之间的关联。
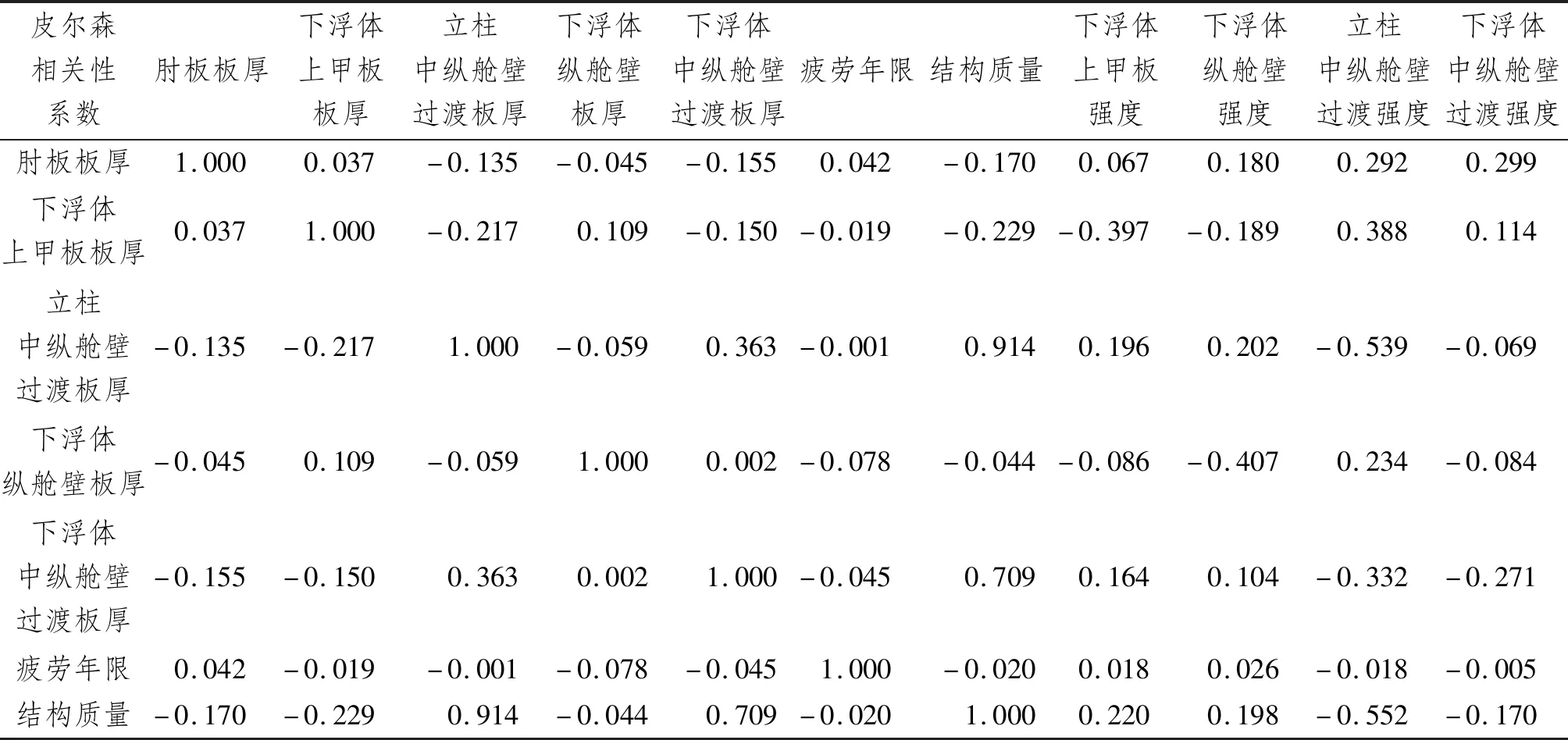
表2 立柱与下浮体连接区域结构分析结果
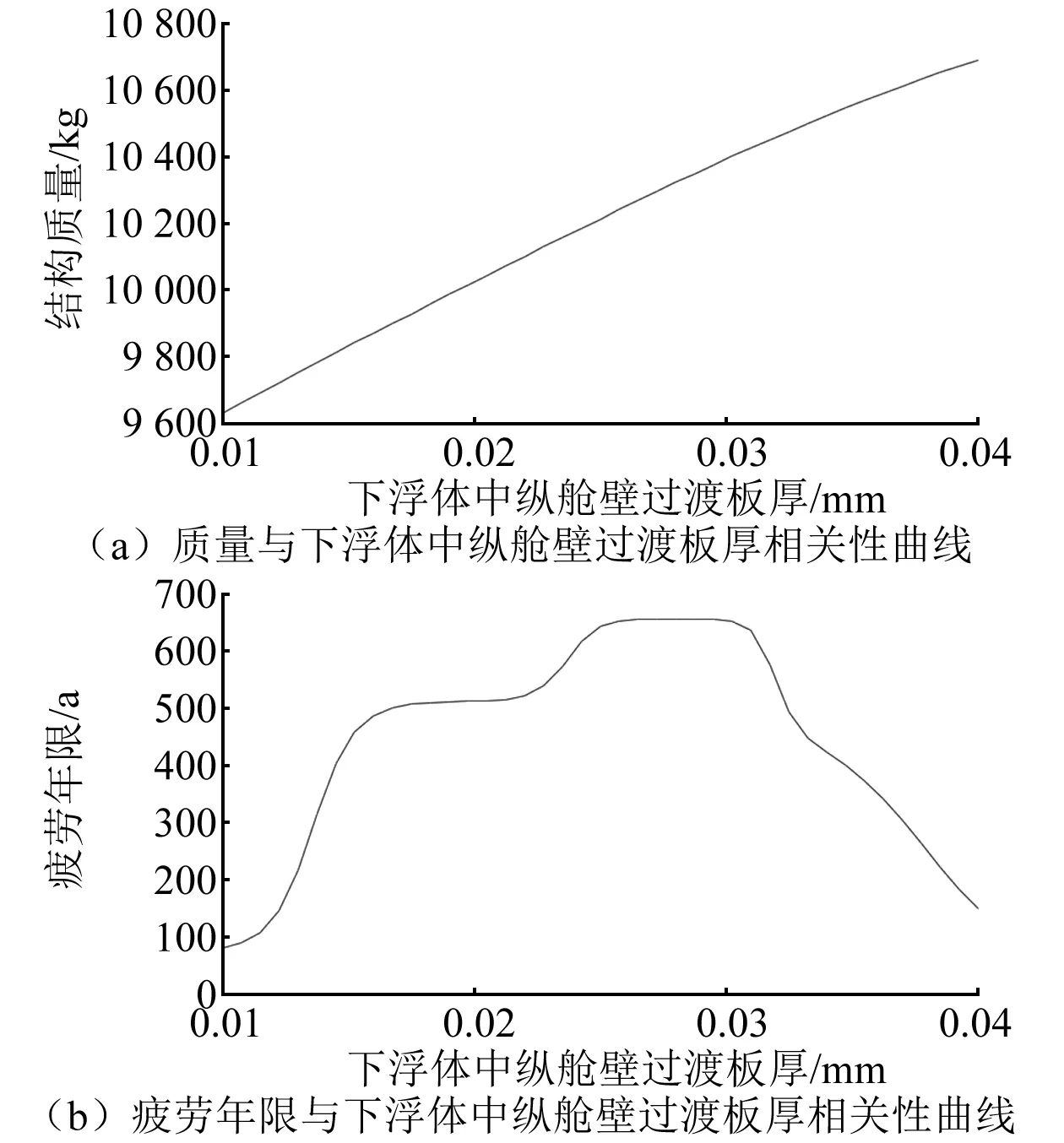
图5 优化目标与浮体中纵舱壁过渡板厚相关性曲线
2.4 轻量化神经网络模型及预测数据分析
本设计计算样本空间较大,单次仿真时间较长,为快速地判断设计空间、预测结构性能,基于试验设计结果,建立响应面模型。按照Optimus轻量化神经网络训练功能,设定单次训练集中的样本数量(EPOCH)为2×105,最大训练误差为0.01,隐藏层的数量设置为8,通过神经网络建立输出与输入之间的回归模型。神经网络通过获得输入数据,计算输出数据,同时计算误差,通过更改权重减小误差。经过不断迭代,达到目标值。图6是计算迭代过程。

图6 神经网络工作流程

(2)
(3)
(4)
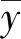
所建立的轻量化神经网络模型以16个肘板设计参数作为输入参数,质量与疲劳年限作为输出,训练样本为不同参数组合的计算数据,然后选取部分仿真数据验证模型的准确性,以达到复杂流程的预测研究。对应于输出参数的响应面检验指标如表3所示,质量响应面与疲劳寿命响应面都有较高的精度,可用于后续优化。

表3 响应面检验指标
此外,对于肘板不同部位的强度,也输出响应面模型,用于对强度的校核和检验,其中典型的几个模型预测结果如图7所示。

图7 响应面及拟合精度
2.5 机器学习探索设计空间
根据对设计空间的研究,质量与疲劳年限目标存在一定冲突但又并非简单的绝对冲突负相关,如果需要同时满足这两个指标,需进行多目标优化。
使用Optimus中的机器学习算法对设计目标进行优化,程序自动在设计空间范围内,从初始种群开始,每次迭代重新构造响应面模型,对非线性较高的区域,自动增加样本点,建立高质量的模型,用机器学习的方式探索设计空间,基于响应面模型,自动对比不同的优化算法,选择合适的算法。通过筛选,程序选择多目标优化问题的非受控排序遗传算法[6](Non-dominated Sorting Differential Evolution)进行设计空间探索,寻找同时满足质量最小化和疲劳年限最大化的最优方案。对于2个目标的问题,帕累托(Pareto)前沿是一系列的点,所有的解构成Pareto最优解集,可供设计者根据不同的权重关系选择最优的方案。
多目标遗传算法是用来分析和解决多目标优化问题的一种进化算法,其核心就是协调各个目标函数之间的关系,找出使得各个目标函数都尽可能达到比较大的(或比较小的)函数值的最优解集。算法流程如图8所示。

图8 多目标遗传算法流程
首先,对种群P(t)进行选择、交叉、变异操作,形成新种群Q(t);然后,合并这两个种群,并对合并后的种群执行非支配排序;最后,将根据个体等级形成的计算前沿Fi从低到高依次加入下一代种群P(t+1),当Fi加入使种群大小越界时,依据拥挤距离从大到小,将个体加入种群。
优化结果如图9所示,从Pareto前沿分布情况可知:当设计重量在8 800~9 800 kg时,2个优化目标呈现出较为线性的变化趋势;当设计重量接近9 900 kg时,出现了较为明显的突变;当设计重量在9 800~10 000 kg时,增加一定的结构板厚和材料等级可非常明显地提高关键区域结构的疲劳寿命。因此,在方案选取时,在重量控制要求内,可优先考虑相应的设计方案,如表4所示。
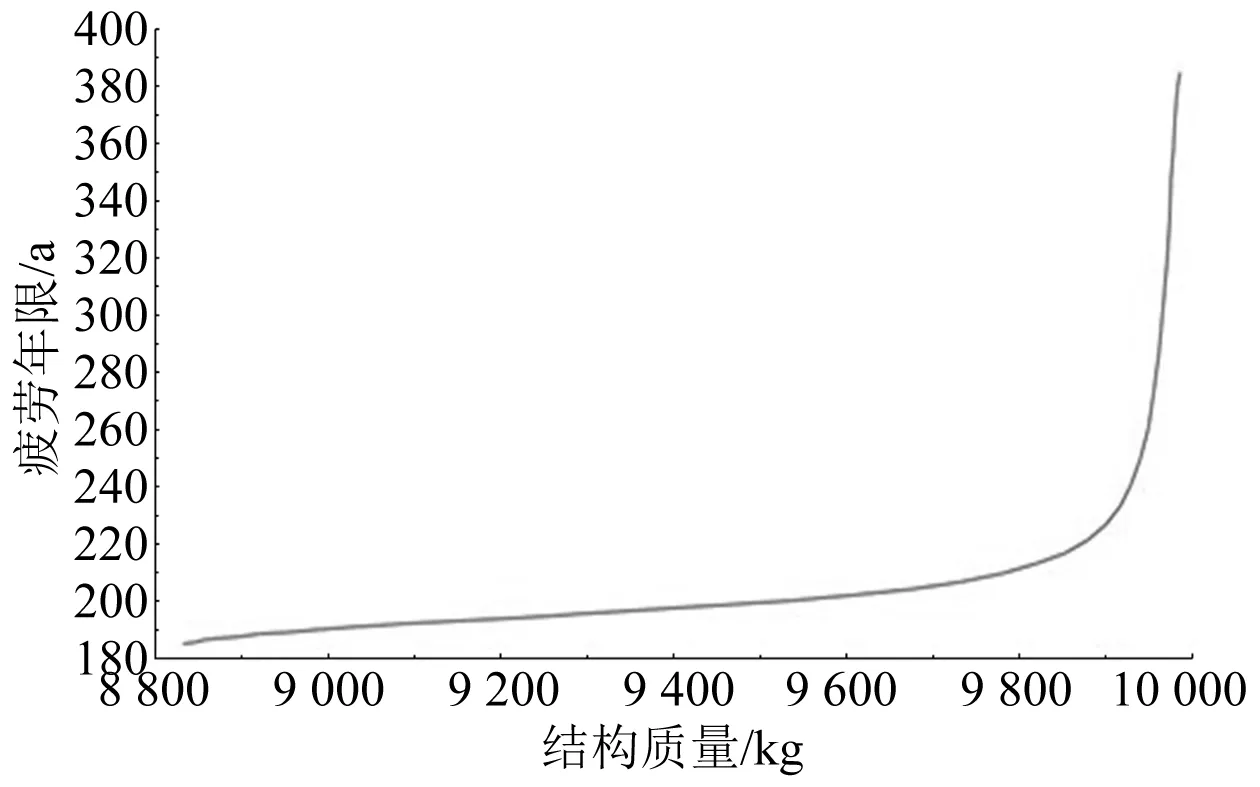
图9 Pareto优化结果和Pareto前沿

表4 不同设计优化方案数据分析

续表4 不同设计优化方案数据分析
3 结 论
半潜式平台关键结构强度是保证平台整体安全的重要环节,在平台总强度分析的基础上,对关键连接区域结构开展细化分析是设计的必要环节和船级社审图检验的关注重点之一。本研究在优化分析平台上进行二次开发,搭建关键结构优化设计分析工作流,整合设计分析软件,形成便于应用的自动化分析模板。总结一套由分析模型参数化开始,经确定设计输入参数、设计优化目标和设计约束边界,到采用数值优化算法和试验设计,最后得到一组有效的设计优化方案,可供参考和选择。
从目前研究的情况来看,主要困难和障碍在于设计数据库单一和可供机器学习的素材不足。结构参数化模型的搭建及相应模型参数化仍是优化分析的主要壁垒之一。若能突破设计方案图纸和数值计算模型之间的壁垒,则后续优化设计和分析会有更加广阔的未来。
