基于VaR-TGARCH模型的中证5G通信主题指数实证分析

张 航， 黄 芮， 郑继明

(重庆邮电大学 理学院， 重庆 400065)

国内通信行业上市公司股票价格波动受到的影响呈现出先小后大再变小的总体趋势[1]。2019年6月6日工信部正式发放5G牌照，预示着中国正式进入5G元年。为了能够很好地评估股票市场的风险性，本文选取了中证5G通信指数作为研究对象。

胡艳妹[2]基于GARCH类模型，运用VaR与CVaR值对中小板市场的风险进行了实证分析，提出了如何降低风险的建议。杨冉冉[3]通过使用计量风险模型——β系数法、现代流行的波动率模型和VaR值理论，对中信证券和华泰证券股票的市场风险性进行研究，提出VaR模型可以用来调节在证券市场中金融产品的发行和交易过程中的风险。刘梦佳[4]以上证综合指数和深圳成分指数为研究对象，选取最优假设分布GARCH-GED模型进行股市波动溢出效应研究，认为上海和深圳两个地区的股市之间存在着上海股市对深圳股市的单向波动溢出。

本文的研究对象是中证5G通信主题指数(指数代码：931079)。该指数以中证全指指数(指数代码：000985)为样本空间，选取其产品和业务与5G通信技术相关的上市公司作为指数样本。截至2021年3月16日，该指数中共包括59只股票，前五大权重股为立讯精密、中兴通讯、歌尔股份、三安广电、兆易创新。本文所有股票数据均来源于同花顺软件(版本号：v8.80.16)，建模分析软件为Eviews软件(版本：9.0)。

1 模型简介

1.1 ADF检验

时间序列的平稳性是均值模型建立的前提，下面简要介绍经典的ADF检验[5]。

假设某一时间序列收益率{rt}的不确定性部分可以由过去的p+1期历史数据描述，即生成过程是服从如下的AR(p+1)过程：

(1-φ1L-φ2L2-…-φp+1Lp+1)rt=at

(1)

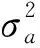
对rt进行单位根检验的检验式为

(2)

以上是不带截距也不带趋势的ADF单位根检验，此外根据序列真实的确定性影响机制，还存在带有截距项和截距趋势项的单位根检验。由于这3类检验方法大致相同，根据Eviews软件可直接得出，不再赘述。

1.2 ARMA模型

ARMA模型也叫移动平均自回归模型[6]，是自回归模型和移动平均模型的组合，常用来估计平稳的不规则波动和时间序列季节性变动，能够有效研究时间序列的波动性。若{rt}序列服从(p,q)阶的自回归移动平均模型，则其ARMA(p,q)模型的表达式为

rt=φ1rt-1+φ2rt-2+…+φprt-p+at-θ1at-1-…-θqat-q

(3)

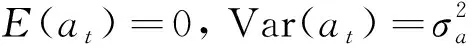
1.3 ARCH模型及其扩展

(4)

式中：{εt}为均值为0、方差为1的独立同分布随机变量序列，通常假定其服从标准正态分布、t分布或者广义误差分布(GED分布)等；α0>0,αi≥0(i=1,2,…,p)；at为扰动项；p为ARCH模型的阶数。

GARCH模型又称为广义ARCH模型，是ARCH模型的拓展，能够有效减少模型对参数的限制，由Bollerslev发展而来[7]。GARCH(p,q)模型为

(5)

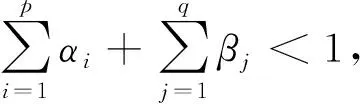
由于GARCH模型的参数限制为正，也就间接地忽略了对称性带来的影响，于是为了探求股票市场的非对称性，ZaKoian提出TGARCH模型[3]，具体形式为

(6)

(7)

若γ≠0，则说明时间序列存在非对称效应。当γ>0时，若at-1<0，利空消息的冲击效应为α+γ倍；若at-1<0，利好消息的效应为α倍。若γ<0时，则存在“反杠杆”效应，即利好消息比利空消息冲击更大。

1.4 VaR模型及其准确性检验

根据菲利普·乔瑞的定义，VaR可以简单表述为[9]：在正常的市场条件下, 给定的置信水平的一个持有时间内某种风险资产的最坏预期损失。在VaR计算中比较简单且常用的方法是方差-协方差法，该方法基于过去的历史数据，对分布均值、方差、协方差等参数进行估计，同时对VaR值进行估计。

由于方差-协方差法是参数法，故波动方差模型{εt}的分布假定尤为重要，常用的假定分布为正态分布、t分布和广义误差分布(GED)分布[4]。正态分布具有集中性、对称性、可加性，是一切分布的极限分布；t分布有很强的厚尾性，当其自由度趋于无穷大时，近似于正态分布；广义误差分布可以理解为这两种分布的结合，有着很强的灵活性，在风险度量理论中可以用来衡量一个分布的厚尾特征。

采用随机序列{εt}服从上述3种分布的TGARCH模型，对中证5G通信主题指数进行建模分析。因此最初就假设收益率序列{rt}服从这3种分布的一种，得出计算VaR的公式[3]为

(8)

式中：Z1-α为给定置信水平α，收益率序列的分位数；Δt为持有收益率序列的时间；ω0为初始资产值；σt为由波动方差模型预测的条件方差序列。本文采用误差服从上文所述3种分布的TGARCH模型，对中证5G通信主题指数进行建模分析。

为了评价VaR计算的效果，需要对其进行准确性检验，目前常用的方法是Kupiec在1995年提出了失败率检验方法[3]，此方法的主要思路是将实际收益率高于VaR值的记成一次“失败”，实际收益率低于VaR值的记成一次“成功”。通过计算相应的概率来判断VaR值是否合理。

LR=-2ln[(1-α)T-NαN]+

(9)

当样本足够大的时候，LR统计量服从自由度为1的卡方分布。于是若计算出的LR值大于其临界值，则拒绝原假设，就可以说明该VaR模型无效；同理，若LR值小于其临界值，则认为通过了准确性检验。

2 实证分析

2.1 数据选取

选取中证5G通信主题指数作为样本(股票指数：931079)，样本范围自2019年8月29日到2020年12月31日，总共326组数据，后文中该指数统称为5G通信指数。

用rt表示第t日的收益率，即Eviews中的{RT}序列，st表示第t日的收盘价，则st-1就是第t-1日的收盘价，收益率定义为

(10)

2.2 收盘价和收益率描述性统计

从图1和图2来看，收盘价有两次短时间急促上升的阶段，分别是2020-02-03至2020-02-28以及2020-05-29至2020-07-13，且对数收益率在此期间也呈现出较大的波动性。又选取5G50通信指数(931406)、通信技术指数(931144)、通信设备指数(931160)、CS计算机指数(930651)4个通信行业有关的指数，并建立收盘价波动图，着眼于这两个时间段，发现与5G指数呈现相同的现象。

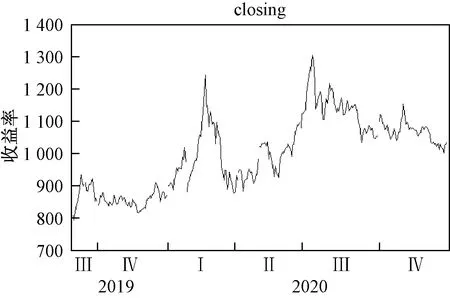
图1 收盘价波动图

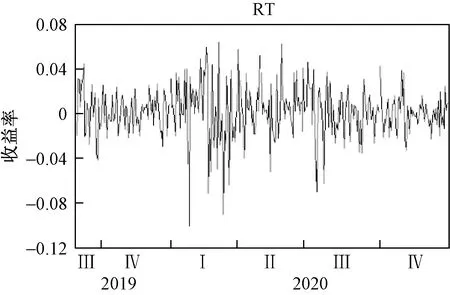
图2 对数收益率时频图

图3为收益率的直方图，通过描述性统计可得收益率序列的偏度为-0.536 496，符合金融序列的有偏性；峰度为5.159 825，相比于标准正态分布，属于尖峰类型；JB统计量为78.760 45，拒绝原假设，说明不服从正态分布。以上分析得知，5G通信指数序列图符合一般金融序列“尖峰、厚尾、有偏”的特性。

图3 收益率描述性统计

2.3 平稳性检验

利用SIC信息准则选定滞后阶数为零，对收益率序列进行ADF检验，由检验结果发现无论在1%、5%，10%的置信水平下，3种情况的t统计量均显著，检验的P值都近似为0，因此拒绝原假设，说明收益率序列是平稳的。

2.4 建立TGARCH模型

2.4.1 ARMA模型建立

根据Box-Jenkins ARMA模型定阶的步骤[10]，首先对收益率序列进行自相关性检验，发现原序列是不存在自相关性的，且ACF和PACF也没有很明显的拖尾和截尾趋势，因此选择利用信息准测进行定阶。选取并建立ARMA(1,1)、ARMA(1,2)、ARMA(2,1)、ARMA(2,2)模型，利用信息准则和系数的显著性检验，最后选定ARMA(1,1)模型作为均值方程。由表1得到具体ARMA(1,1)均值模型的表达式为

rt=0.000 777-0.935 774rt-1+0.986 619at-1。

表1 GARCH(1,1)模型

通过对ARMA(1,1)模型的残差进行自相关检验，发现Q统计量并不显著，即认定残差序列是不相关的，因此模型是优良的。

通过对ARMA(1,1)模型残差平方的自相关检验，初步认为收益率序列存在ARCH效应，为了进一步检验，选取滞后阶数为一阶的拉格朗日乘子检验法，ARMA(1,1)检验结果见表2，Q统计量为8.771 264，P值为0.003 3，故拒绝原假设，即原序列是有异方差性。

表2 ARMA(1,1)异方差检验结果

2.4.2 TGARCH模型的建立

由2.4.1节可知，收益率序列存在异方差性，因此可以建立GARCH模型。疫情期间信息对股票的冲击是不平衡的，因GARCH模型无法衡量股票市场信息的影响效果，预选用非对称的GARCH衍生模型进行拟合。考虑到预测条件方差方面TGARCH模型要优于EGARCH模型[11]，更有利于VaR模型预测风险，于是选用TGARCH模型建立模型。

根据信息准则和系数的显著性检验，最终选取阶数p=1、q=1的TGARCH(1,1)模型，见表3，得到该模型的数学表达式为

表3 TGARCH(1,1)模型

2.5 VaR计算

2.5.1 VaR估计值描述性统计

由2.4.2节可知，收益率序列存在杠杆效应，因此选择TGARCH模型进行VaR的计算为佳。又因上述模型中随机序列{εt}是服从正态分布的，再依次建立服从t分布和GED分布的TGARCH(1,1)模型，根据结果的自由度，在给定置信水平为95%和99%下，可以算出它们各自的分位数，见表4。

表4 基于TGARCH模型分位数

得出分位数后，根据式(8)便可以计算出这6种情况的VaR值，并进行描述性统计，得出均值、标准差、最大值、最小值的统计特征，见表5，随后联合收益率序列建立波动图，如图4所示。

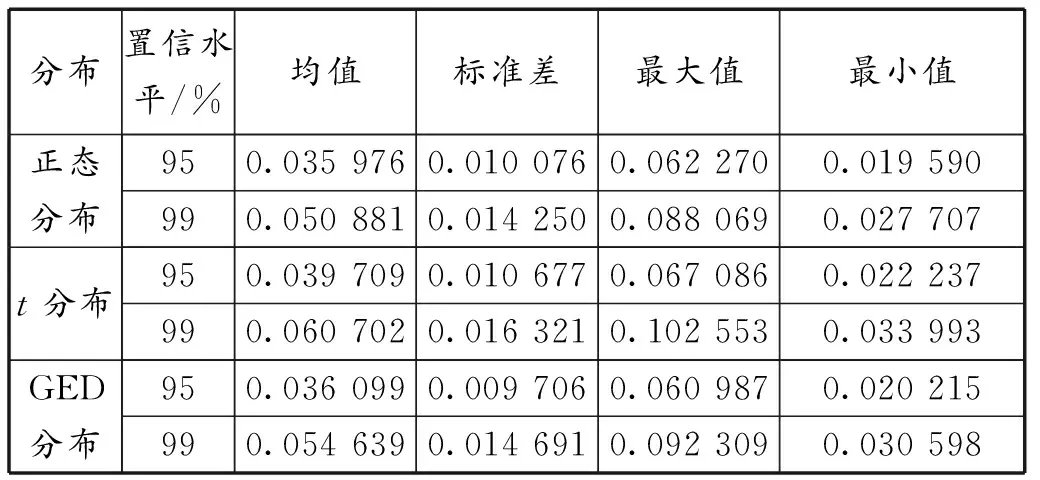
表5 VaR估计值描述性统计

从表5可以看出，在置信水平一定的情况下，3种分布的VaR值相差不大，从3种分布下的波动图4中可以得出如下结论：①无论是在哪种分布下，99%的置信水平下均比95%置信水平下的预测值更高；②3种分布的图形走势都与收益率序列大致相同；③从预测风险值来看，t分布和GED分布在99%显著性水平下的预测风险值明显比正态分布的高。

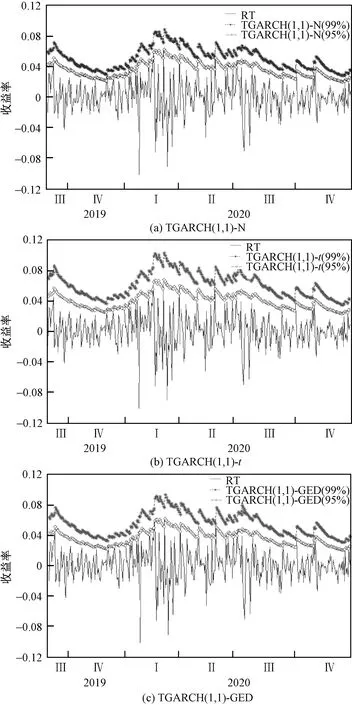
图4 波动图

2.5.2 VaR的准确性检验

根据2.5.1节的预测波动图(图4)可以看出，99%置信水平下的VaR值过高地预测了风险，因此选择95%置信水平，即显著性水平为5%，进行VaR的准确性检验。

本次检测的样本容量T=325，期望失败天数为T×5%=16.25 d，根据1.4节介绍的失败率检验方法，可以统计出实际失败天数，并根据式(9)算出3种分布假设下的LR统计值。由表6可知，3种假设分布的LR值均小于临界值，于是此3种模型均可认定有效。就实际失败天数来看，TGARCH-t更接近实际情况；就实际失败率方面，TGARCH-N和TGARCH-GED实际失败率均大于5%，过高地预测了风险。

表6 VaR回测检验结果

最后综合考虑，确定基于t分布的TGARCH模型为最优拟合模型。

3 总结与建议

选取中证5G通信指数作为研究对象，通过对收益率序列进行描述性统计，发现5G指数具有“尖峰厚尾、有偏”等特性。结合序列特性，建立ARMA(1,1)模型和GARCH(1,1)模型，并很好地拟合了数据；建立TGARCH(1,1)模型，通过非对称项系数确定收益率存在杠杆效应，且好消息的冲击比坏消息的冲击要大，这也一定程度上解释了疫情稳定期阶段股票迅速上升的原因。

VaR风险计算方面，通过对预测风险值的描述性统计，发现基于TGARCH模型下，不同分布计算出来的VaR值整体差异性是不大的。VaR回测检验结果是优良的，且通过了Kupiec检验，并且95%显著性水平下的实际失败率都是在可接受范围内的，最后结合LR统计值和实际失败率，认为TGARCH-t模型预测效果最好。由于本文关于VaR的计算采用的是参数法，对分布的要求较高，后续还可以尝试用非参数法进行风险值的计算。