梁桥桥墩纵桥向计算长度系数研究
2021-09-04陈国红徐召
陈国红, 徐召
(山东省交通规划设计院有限公司, 山东 济南 250031)
1 梁桥桥墩计算长度系数研究
梁桥桥墩的结构形式有柱式墩、空心墩、薄壁墩等。关于桥墩的计算长度,各国规范给出了不同的计算长度系数取值(表1)。JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》给出了4种经典约束状态的计算长度系数取值;美国AASHTO规范还给出了一侧固定但另一侧固定端可侧移的桥墩计算长度系数取值;英国BS 5400规范在美国规范的基础上给出了单侧固定单侧为不可滑移弹性约束(固定橡胶支座)桥墩计算长度系数的取值。由上可以看出:不同边界条件下,中国规范取值采用经典解,取值相对较小,美国规范次之,英国规范最为保守。实际工程中,墩底可根据桩基弯矩零点或者刚性承台台顶确定固结点,墩顶的约束方式有滑动约束、固定约束、弹性索约束、墩梁固结等多种形式,单个桥墩墩顶还要受到其他墩台水平刚度的约束,其计算模式很难用表1中的约束方式来界定。
单墩墩顶的约束可以分为墩梁固结和墩梁支座连接两种方式,已有不少学者在桥墩计算长度系数取值方面开展了研究工作。对于墩梁采用支座连接的梁桥,文献[6]采用有限元计算软件对某装配式桥梁进行稳定分析,通过失稳荷载来反推桥墩计算长度系数取值;文献[7]采用有侧移框架的单阶柱的简化模型,对一座刚构桥的桥墩计算长度开展了研究,根据墩顶的约束方式按照自由和可侧移两种方式进行了模拟,未考虑一联桥梁其他桥墩的影响;文献[8]采用有限元计算软件对刚构桥稳定性开展了研究,给出不同工况下桥墩的稳定系数,对于桥墩的计算长度系数取值并无明确说明。

表1 各国规范对桥墩计算长度系数的规定
总体来看,关于桥墩计算长度系数的研究,一般只考虑了墩顶的水平约束。因此,为了更全面地研究桥墩的力学特点及精确地完成桥墩承载能力受力分析,有必要对梁桥桥墩计算长度系数的合理取值开展深入研究。
2 桥墩的稳定方程
2.1 方程的建立
桥墩为偏心受压构件,墩底可根据桩基弯矩零点(单排桩)或者刚性承台台顶(多排桩)确定固结点,墩顶一般为弹性约束[图1(a)],不同桥墩墩顶的约束方式可简化为图1(b)所示的计算模型,所不同的是墩顶水平约束刚度k和扭转约束刚度kθ。
如图1(c)所示,当墩顶轴力Fn达到临界荷载时,桥墩的平衡路径将发生分支,即除可保持原直线形式的平衡状态外,还可能发生挠曲形式的平衡状态;在寻求平衡状态的分支点时,只要求杆件发生微小的挠曲,因此杆件的曲率可以用y″近似表示。取任意截面上端隔离体为研究对象,其弯矩平衡方程可以表达为:
EIy″=Fn(Δ-y)-Fk(h-x)-Mθ
(1)
式中:Fk为墩顶水平弹性约束力;Mθ为墩顶扭转约束力;Δ为墩顶水平位移;θ为墩顶转角;E为桥墩材料的弹性模量;I为桥墩的抗弯刚度;h为桥墩高度。
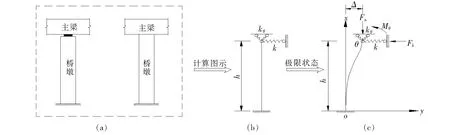
图1 桥墩稳定计算简图
Fk、Mθ可按下式确定:
Fk=kΔ
(2)
Mθ=kθθ
(3)
令:
(4)
桥墩极限稳定荷载Fn的一般表达式为(μ为桥墩的计算长度系数):
(5)
将Fn代入式(4)可得桥墩的计算长度系数μ为:
(6)
将式(1)两端除以EI并代入式(4)后可得:
(7)
式(7)的通解为:
(8)
引入位移边界条件:x=0处,y=0、y′=0;x=h处,y=Δ、y′=θ;可得到一组关于未知参数A、B和Δ、θ的齐次线性方程组:
(9)
要使参数A、B和Δ、θ不全为零的条件是方程的系数行列式等于零,即:
(10)
桥墩的抗推刚度为:
(11)
令墩顶的纵向约束刚度k与桥墩的抗推刚度k′之比为m:
(12)
桥墩的线刚度i为:
(13)
令墩顶的扭转约束刚度kθ与桥墩的线刚度i之比为n:
(14)
则式(10)可以简化为:
(15)
展开式(15)可得关于αh、刚度比m及n的方程:
(16)
2.2 方程的求解
式(16)即为桥墩的稳定方程,当刚度比m及n为确定值时,它是一个关于αh的超越方程。稳定方程(16)为多解方程,一般最小特征解对应于桥墩的计算长度系数取值。将方程(16)左右看成不同的表达式:
F(αh,1)=tan(αh)
则可采用图2所示的图解法求解。
对于图2(a)~(c),αh的最小特征解处于π/2~3π/2,相应的桥墩计算长度系数取值为0.666~2.0;当刚度比m=0、n=0,αh的特征解为π/2,此时桥墩的计算长度系数为π/(αh)=2,即为一端固定一端自由受压柱计算长度系数的经典解;当刚度比m=10、n=4时,αh的特征解为3π/2,此时桥墩的计算长度系数为π/(αh)=0.666。随着刚度比m及n的不断增大,桥墩的计算长度系数不断减小,αh的第一特征解(π/2~3π/2)为虚解[图2(f)],第二特征解大于3π/2且小于2π,此时,桥墩的计算长度系数为0.666~0.5;计算表明:当刚度比m=100、n=100时,桥墩的计算长度系数为0.505,已经非常接近两端固结受压柱计算长度系数的经典解0.5。不同刚度比m及n下桥墩的计算长度系数计算结果见表2。

图2 图解法计算示意图
由表2可以看出:当m<3.0时,提高墩顶的抗扭刚度可以显著降低桥墩的计算长度系数;当3.0

表2 不同刚度比下桥墩计算长度系数理论值
2.3 简化计算公式
为了方便工程应用,表2中数据可以拟合得到以下简化计算公式:
当m≤2.4,n≤2.4时:
μ=1.842-0.266 6n-0.409 8m+0.025 13n2+0.104 1mn+0.039 88m2
(17)
当m>2.4,n>2.4时:
μ=0.530 4+0.146exp(-0.115 8n2)+0.548 4·exp(-0.184 4m2)
(18)
式(17)与精确数据比较,均值为0.974 9,方差为0.030 75;式(18)与精确数据比较,均值为0.968 1,方差为0.039 12。
3 桥墩墩顶刚度计算
3.1 基本假定
梁式桥梁一般采用简支或者连续结构,为了便于分析,现做如下假定:
(1) 桥梁的轴向刚度一般是桥墩抗推刚度的1×103~1×105倍,桥梁轴向可视为刚体。
(2) 滑动支座处支座与梁体在正常使用状态下可以发生支座与梁体间的相对滑移,即滑动支座的抗推刚度为k=0。
(3) 非滑动支座(固定支座、橡胶支座等)不考虑其与梁体间的相对滑移。
(4) 墩顶设置支座时,不考虑支座对梁体的转动约束,即kθ=0。
3.2 桥墩墩顶的水平约束刚度k
桥梁结构中的某一个桥墩墩顶水平约束刚度,不仅与墩顶支座(如有)刚度有关,还与一联内其他墩柱与其支座的集成水平约束刚度有关。
图3为某一联桥梁的立面布置示意图,若不考虑共用墩墩顶支座(滑动支座)的水平约束作用,则图中被研究桥墩的墩顶水平约束刚度可采用该桥墩支座水平刚度与其他桥墩刚度(含支座水平约束刚度)并联后形成的集成刚度再进行串联(图4),若计各桥墩墩身的抗推刚度为k桥墩i及相应支座抗推刚度为k支座i(i=1,…,n),则各桥墩的抗推刚度为ki=k支座ik桥墩i/(k支座i+k桥墩i);被研究桥墩墩顶的水平约束刚度为:
k=k支座∑ki/(k支座+∑ki)。
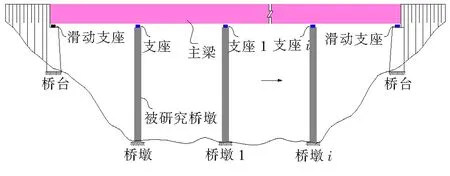
图3 桥梁立面布置示意图
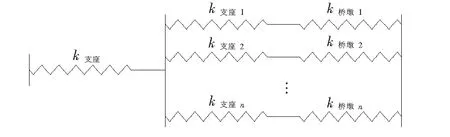
图4 墩顶水平约束刚度k计算示意图
3.3 桥墩墩顶的扭转约束刚度kθ
当一联桥梁结构中的某一个桥墩采用墩梁固结时,墩顶不仅受到其他墩柱的水平约束作用,还受到墩顶主梁的扭转约束作用。仍以图3为例,墩顶处的扭转刚度由主梁提供,对于等高梁桥,可根据临近桥墩墩顶的约束状态按照结构力学位移法经典公式求得,对于变截面连续梁桥,可采用通用软件计算求得,因篇幅关系,该文不再展开叙述。
4 桥墩计算长度的合理取值
4.1 工程实例
以图3为例,桥梁上部结构采用预应力混凝土小箱梁,下部结构为柱式墩,跨径布置为4×30 m。上部结构桥梁宽度为12 m,横向采用4片小箱梁,中心间距2.9 m,梁高为1.6 m;桥墩采用双柱式圆形墩,直径为1.7 m,墩高为20 m(已经考虑了墩底固结点);桥墩处支座采用GYZ 375×77,一个连续墩处支座共计10个,桥台伸缩缝处支座为GYZF4275×65;各构件主要几何参数如表3所示。

表3 主梁及桥墩结构特性参数 kN/m
桥台(共用墩)处一般布置四氟滑板支座,在温度、收缩徐变、车辆荷载等作用下会发生主梁与桥墩间的相对滑移,共用墩一般按下端固结上端可活动的计算模式来考虑,计算长度系数可取为2。连续墩一般设置板式橡胶支座,当一联桥跨数较多时,设计时一般仅在中间的几个墩设置固定支座,为了更好地研究桥墩的计算长度系数,该文研究的共用墩处均设置四氟滑板支座,即不考虑共用墩对其他墩柱水平约束刚度的影响。
4.2 一联桥梁桥跨数的影响分析
中国装配式结构桥梁一联的桥跨数一般不超过6跨。按4.1节的工程实例,根据前述分析,不同桥跨数下连续墩的计算长度系数见表4。由图4可以看出:随着一联桥梁桥跨数的增加,桥墩的计算长度系数逐渐减小,降低幅度随着桥跨数的增加越来越小;当桥跨数超过5跨时,每增加一跨,计算长度系数降低值小于0.04,这是由于其他桥墩并联抗推刚度随着桥跨数量的增加不断增大,但是与墩顶支座组成的串联刚度增大幅度在减小的缘故;总体来看,桥墩的计算长度系数在1.4以上。

表4 不同桥跨数下桥墩计算长度系数
4.3 墩顶约束条件的影响分析
当桥墩较高时,可通过设置固结墩的办法来减少支座的使用,减少桥墩的计算长度,提高桥梁的抗推刚度;对于纵坡较大的桥梁,还可以避免主梁纵向滑移。对于4.1节的工程实例,连续墩墩顶不同约束条件下各连续桥墩的计算长度系数见表5。
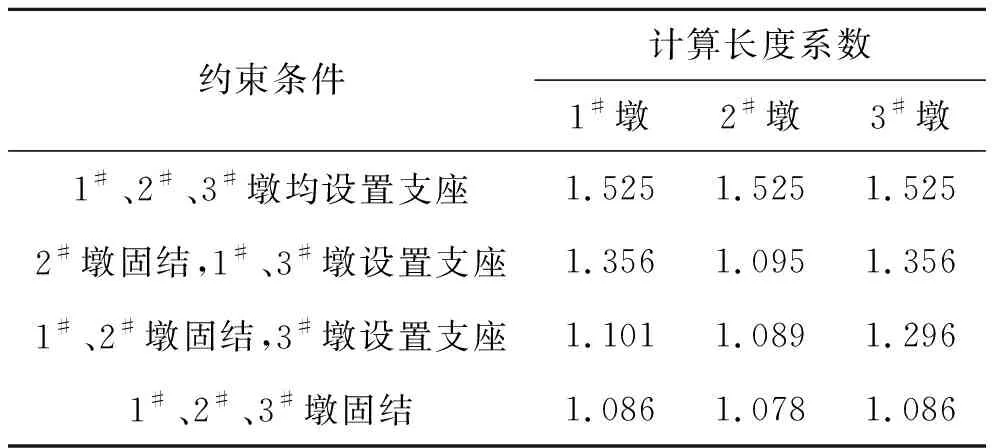
表5 墩顶不同约束下桥墩计算长度系数
由表5可以看出:当一联桥梁设置有固结墩时,可以明显降低各桥墩的计算长度系数;当桥墩均设置支座时,桥墩的计算长度系数接近1.5,当均采用墩梁固结时,计算长度系数接近1.09。
4.4 桥墩高度的影响分析
桥墩高度是桥墩计算长度的重要影响因素,也是设计时合理选择桥墩尺寸的重要依据。对于4.1节的工程实例,不同墩高下桥墩的计算长度系数见表6。
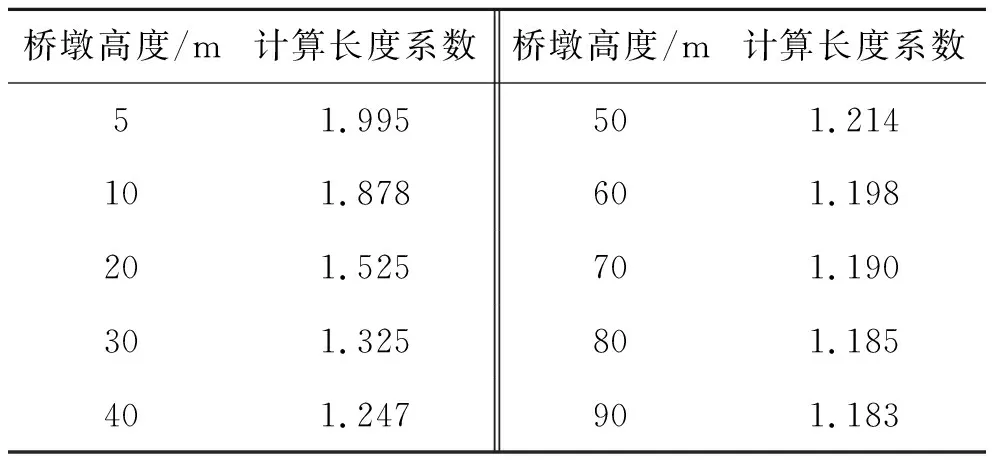
表6 不同墩高下桥墩计算长度系数
由表6可以看出:桥墩的计算长度系数随着墩高的增大逐渐降低;墩高越小,计算长度系数越大,当墩高超过40 m以后,计算长度系数变化幅度不大;随着墩高的增加,计算长度系数趋近于1.18。实际工程中,1.7 m直径的墩柱可以应用的最大高度一般不超过25 m,因此对于设置板式橡胶支座的梁式桥来说,当墩高差异不大时,连续墩的计算长度系数一般为1.4~1.9。
5 结论
采用静力法建立墩底固结墩顶具有弹性约束的桥墩弯矩平衡微分方程,给出不同约束条件下桥墩计算长度系数的数值解并拟合了简化公式,得到以下结论:
(1) 当确定了桥墩基础固结点时,桥墩的计算长度系数与墩顶的纵向约束刚度k和桥墩的抗推刚度k′之比m、墩顶的扭转约束刚度kθ和桥墩的线刚度i之比n有关;刚度比m、n越大,桥墩的计算长度系数越小,当m、n为0时,桥墩的计算长度系数为2.0,当m、n趋于无穷大时,桥墩的计算长度系数接近0.5;由于抗推刚度比m一般小于3.0,桥墩的计算长度系数一般大于1.0。
(2) 对于设置支座的装配式结构桥梁,随着一联桥梁桥跨数及各桥墩墩高的增加,桥墩计算长度系数逐渐减小,一般为1.4~1.9,设计时,应根据不同的刚度比合理取值。
(3) 当一联桥梁中设置有固结墩时,能大大减小桥墩的计算长度系数,固结墩的计算长度系数为1.0~1.1。
