扫描电子显微镜放大倍数示值误差的校准及不确定度评定*

韩强 骆彬威 张欣宇,2

开发设计

扫描电子显微镜放大倍数示值误差的校准及不确定度评定*

韩强1骆彬威1张欣宇1,2

（1.广东省计量科学研究院，广东 广州 510405 2.广东省现代几何与力学计量技术重点实验室，广东 广州 510405）

扫描电子显微镜是用于微观表面形貌观察、显微结构分析以及微纳米几何尺寸测量的常用分析仪器。由于仪器扫描图像时易出现放大倍率的偏差，导致图像畸变以及测长不准等问题，因此放大倍数示值误差是该类仪器校准的主要计量特性。利用微米至亚微米尺度一维线间距标样实现对扫描电子显微镜放大倍数示值误差的校准，并对校准结果的不确定度进行评定。

扫描电子显微镜；格栅间距；放大倍数；示值误差；不确定度

0 引言

随着我国微纳米检测技术的进步和相关产业的不断发展，对微纳米几何尺寸的精确测量需求也越来越多。扫描电子显微镜作为纳米材料和微纳米结构尺寸表征的重要工具，在高校、科研院所和高科技企业的应用日益普遍。目前，在校准扫描电子显微镜时，依据国家和相关部门的相关计量检定规程，主要对放大倍数示值误差、放大倍数重复性、图像的线性失真度（图像畸变程度）、二次电子像分辨本领等计量特性进行校准，其中放大倍数示值误差是扫描电子显微镜最重要的计量特性[1-2]。随着电子显微技术的发展以及纳米标准样品研究的突破，国内较多采用微米至亚微米级别一维和二维光栅、一维线间距、二维格栅或纳米颗粒等标准样品校准扫描电子显微镜的放大倍数示值误差，对放大倍数的校准也转变为对图像显微标尺的校准，避免了计算放大倍数绝对值的问题[3-5]。

本文以多功能标准样板为标准器，利用其可溯源至中国计量科学研究院的微米至亚微米尺度一维线间距值，实现对扫描电子显微镜不同放大倍数示值误差的校准，并对校准结果的不确定度进行评定。

1 校准方法

1.1 校准依据

本文对扫描电子显微镜放大倍数示值误差的校准依据为JJG 550—88《扫描电子显微镜试行检定规程》。

1.2 计量标准设备

本文采用的主要计量标准设备为多功能标准样板，包括5种不同的线间距尺寸，分别为50 μm， 10 μm，2 μm，1 μm和0.5 μm；测量范围覆盖100×～200000×；线间距值均溯源至中国计量科学研究院。计量标准器具的详细信息如表1所示。

表1 计量标准器具及配套设备

1.3 被校对象

被校对象为工作放大倍数为200000 ×以下的扫描电子显微镜。

1.4 校准方法

扫描电子显微镜的放大倍数误差利用包含5个不同线间距值的标准样板进行测量。针对不同放大倍数，分别选用50 μm，10 μm，2 μm，1 μm和0.5 μm线间距进行测量计算。

校准时将标准样板放置于扫描电镜样品室中，抽真空后，对样板进行放大观察；设置放大倍数至所需倍率；调整样品台角度或利用软件进行图像旋转，使标准间隔线的走向分别与显示器的上下或两侧边框平行；添加标尺并保存图像。

由于不同的显示设备，人眼实际观察到的图像放大倍数并不相同，所以扫描电子显微镜放大倍数示值误差可以利用图像中标尺的放大倍数示值误差来表示。利用钢直尺分别测量图像中标尺的实际长度和线间距的实际长度；再分别除以标尺的标称长度和线间距的标称长度，可得到标尺显示的放大倍数和图像的实际放大倍数；两者之差再除以图像的实际放大倍数即可得到标尺的放大倍数示值误差，即扫描电子显微镜的放大倍数示值误差。

利用多功能标准样板的2 μm和0.5 μm线间距，校准扫描电子显微镜放大倍数示值误差，获得的图像如图1所示。

图1 利用线间距值校准放大倍数示值误差的扫描电子显微镜图像

2 数学模型

扫描电子显微镜放大倍数示值误差的计算公式为

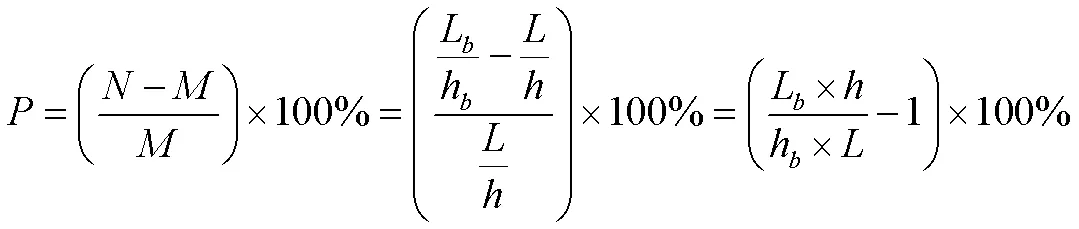
式中，为放大倍数示值误差；为标尺显示的放大倍数，×；为图像的实际放大倍数，×；L为标尺的实际长度，mm；h为标尺的标称长度，μm；为线间距的实际长度，mm；为线间距的标称长度，μm。

由于各输出量间不相关或相关性较弱，为简化起见，均按不相关处理，则可得到

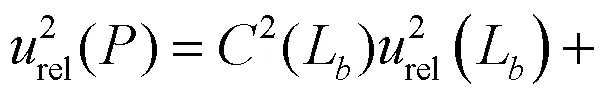
3 校准结果的不确定度评定

3.1 标准不确定度评定

长度在300 mm内的钢直尺，其MPE为±0.10 mm，按均匀分布处理，则由钢直尺不准导致的标准不确定分量为

钢直尺的最小刻度为1 mm，观察100×～200000×下得到的多幅图像中线间距尺寸，估计出由标尺边界不清晰造成的测量误差基本可控制在1 mm之内，则其区间半宽度为= 1/2 = 0.5 (mm)，按均匀分布处理，由标尺边界不清晰导致的标准不确定度分量为

由标尺实际长度测量不准引入的不确定度分量为

线间距实际长度与标尺实际长度在同一幅扫描电镜图像上利用相同的仪器（钢直尺）进行测量，因此线间距长度测量误差引入的不确定度分量同样由测量仪器（钢直尺）不准引入的标准不确定分量及线间距边界不清晰引入的标准不确定分量组成。利用钢直尺测量时所使用的最短测量尺寸同样设为100 mm，同3.1.1计算可得到

由线间距实际长度测量不准引入的不确定度分量为

根据校准证书可知：线间距为50 μm时，C= 0.13 μm；线间距为10 μm时，C= 0.03 μm；线间距为2 μm时，C= 5.9 nm；线间距为1 μm时，C= 2.5 nm；线间距为0.5 μm时，C= 2.4 nm。半宽高按正态分布处理，包含因子取2，则计算不同放大倍数下的不确定度分量公式为

计算得到不同放大倍数下的线间距标称长度不准引入的不确定度如表2所示。

3.2 合成不确定度

3.2.1 标准不确定度分量汇总如表3所示。

3.2.2 合成不确定度计算

合成不确定度计算公式为

计算得到不同校准范围内合成不确定度如表4所示。

表2 线间距标称长度不准引入的不确定度一览表

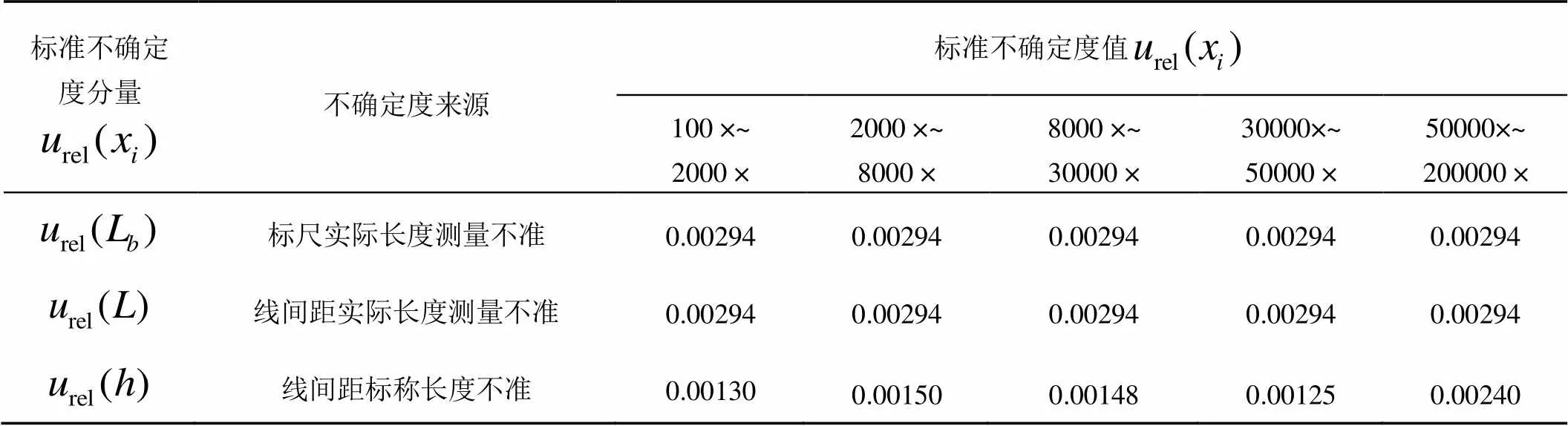
表3 标准不确定度分量汇总表

表4 放大倍数误差校准结果的合成不确定度一览表

3.3 扩展不确定度计算

取包含因子= 2，则有

计算得到不同校准范围内放大倍数误差校准结果的扩展不确定度如表5所示。

表5 放大倍数误差校准结果的扩展不确定度一览表

4 结语

本文利用量值可溯源至中国计量科学研究院的多功能标准样板，通过测量扫描电子显微镜扫描图像中微米至亚微米尺度线间距的实际值及图像中显微标尺的实际值，计算得到标尺显示的放大倍数示值误差，从而实现了扫描电子显微镜放大倍数示值误差的校准。通过对校准结果进行不确定度分析和评定，为扫描电子显微镜校准中放大倍数示值误差这一重要的计量参数，提供了不确定度评定实例。

[1] 上海市标准计量管理局. JJG 550—88扫描电子显微镜试行检定规程[S].北京:中国计量出版社,1988.

[2] 国家教育委员会. JJG（教委）010—1996分析型扫描电子显微镜检定规程[S].北京:科学技术文献出版社,1997.

[3] 张欣宇,凌珊,封小亮,等.扫描电子显微镜校准方法[J].计测技术,2015,35(6):45-49.

[4] 钱进,石春英,谭慧萍,等.利用一维光栅标样校准扫描电子显微镜方法的研究[J].计量学报,2010,31(4):299-302.

[5] 周剑雄,陈振宇.微米-亚微米级扫描电镜图像放大倍率校准标样的研制报告[J].电子显微学报,2006(S1):149-150.

Calibration and Uncertainty Evaluation of Magnification Indication Error of Scanning Electron Microscope

Han Qiang1Luo Binwei1Zhang Xinyu1,2

（1.Guangdong Institute of Metrology, Guangzhou 510405, China；2.Guangdong Provincial Key Laboratory of Modern Geometric and Mechanical Metrology Technology, Guangzhou 510405, China）

Scanning electron microscope is a common analytical instrument for micro surface morphology observation, microstructure analysis and micro nano geometry measurement. Because the magnification deviation is easy to occur when the instrument scans the image, resulting in image distortion and inaccurate length measurement, the indication error of magnification is the main metrological characteristic of this kind of instrument calibration. The calibration of magnification indication error of scanning electron microscope is realized by using one-dimensional line spacing standard sample from micron to submicron, and the uncertainty of calibration results is evaluated.

scanning electron microscope; grill space; magnification; indication error; uncertainty

韩强，男，1979年生，硕士研究生，工程师，主要研究方向：纳米计量检测。E-mail: 13922271512@139.com

TB92；TN16

A

1674-2605(2021)04-0008-05

10.3969/j.issn.1674-2605.2021.04.008

基金项目：国家重点研发计划资助项目（2018YFF02123404）