基于颗粒离散元法的涵洞式水闸上覆填土应力位移场变化特征分析研究

2021-09-03高飞

水利科技与经济 2021年8期

高飞

(广东粤源工程咨询有限公司，广州 510635)

1 概述

水闸的设计与运营是水利工程中重要研究课题，其中又以涵洞式水闸结构设计为难点，开展涵洞式水闸安全稳定性设计以及结构验算对工程质量安全具有重要作用[1-3]。涵洞式水闸的稳定性与上覆填土层的负载息息相关，研究填土层力学状态对探讨涵洞安全性具有重要启示作用。由于填土层土料的力学性质与稳定性有关，因而张磊[4]、赵万杰等[5]、魏常琦[6]通过室内精密土工仪器设计开展土体的渗透、力学基础试验，获得土体重要渗流参数和力学参数，为涵洞变形、承载设计提供重要试验依据。另一方面，现场实时获取到的监测数据可较好反映土体稳定性状态，因而一些水闸等水工建筑中布设有监测传感器，通过分析工程现场实际数据，为水利工程运营提供重要预判参考[7-9]。

不论是室内试验亦或是现场监测，一定程度上均是需要大量的精力与成本，而离散单元法作为一种研究土颗粒、混凝土材料的重要仿真计算手段，借助其开展土体等岩土材料在水利工程运营荷载下的力学特征分析，为实际工程提供重要的计算参考[10-11]。本文利用离散单元法与PFC颗粒流软件，建立涵洞式水闸上覆填土层颗粒模型，开展填土层应力、变形场分析，为工程安全设计与运营提供重要参考。

2 离散单元法求解与建模

2.1 工程概况

粤北地区由于水利资源分布不均，规划修建一座水资源中转调度枢纽工程，该枢纽工程包括蓄水池、抽水泵站、拦污栅、承重结构墩、输水灌渠以及涵洞式水闸。承重结构墩承担着泵站所涉及的水工建筑承载作用，直径参数设计为1.2 m，采用C35混凝土一体式浇筑形成，布设有预应力锚索作为支护结构，锚块与拦污栅端面为接触式连接方式，锚块尺寸为0.6 m×1 m，其中，主锚索共有12根，间距设定为60 cm，次锚索可承担1 500 kN张拉吨位，最外侧次锚索位于墩断面内侧30 cm处，确保张拉结构与承重结构具有良好的适应性。所建设的输水灌区总长度跨越为65 km，可实现3.333 3×104hm2农田灌溉，确保灌区即使枯水季缺水率也不超过1%，极大保障了区域内农业用水安全性，弥补了地区内水资源时空不均的现状。

灌区渠道采用土工格栅作为加固材料，一方面提升渠道衬砌结构运营稳定性，另一方面极大保障了输水效率，降低输水损耗度。渠道基础位于低下粉质壤土层中，承载能力适中，土颗粒最大粒径不超过4 mm，含水率为13%～22%，全渠道最大渗透坡降不超过0.2，渗流稳定性较佳。目前，工程设计部门主要针对解决涵洞式水闸可靠性运营。该水闸设计为涵洞输水控水形式，上覆具有一定高度填土，土料主要以壤土、粉质黏土夹杂为主，由于上覆填土应力位移场势必会受到水闸两侧土体影响，造成土压力或沉降位移变化，对水闸长期稳定性具有重要影响，特别是上覆填土与两侧原生土沉降变形差，对水闸会产生显著压力损伤效应[12-13]。为此，笔者主要根据实际水闸工作状态以及土体物理力学状态开展离散元仿真计算，为准确评估涵洞式水闸上覆填土体力学稳定性提供重要参考。

2.2 离散单元法与建模分析

离散单元法主要通过借助颗粒流软件建立颗粒模型，按照实际工况下颗粒荷载约束条件进行应力场、位移场求解。其中，颗粒模型采用Clump模板，按照圆形颗粒生成颗粒集合体，以约束条件作为求解变量，按照颗粒运动场方程求解颗粒模型中离散解[14-15]。本文计算模型中土体最佳含水量采用击实试验中测定值16.8%，压缩模量为7.2 MPa，以室内不固结不排水试验测定抗剪参数分别为31 kPa和30°，土料压实度为80%，按照工程现场填土厚度以及土层状态，本文离散单元法计算中设定水闸顶延伸与底影响宽度比α参数为1，水闸两侧土体边坡坡度β参数为60°，所设计方案几何模型图见图1。

图1 涵洞式水闸几何模型(α=1，β=60°)

本文离散单元法求解主要依靠PFC 3D仿真平台，按照分层构建颗粒模型的原则，逐步建立离散元仿真颗粒模型，从大面积颗粒重叠至消除折叠，再通过移动颗粒模型顶、底板约束条件改变其内部孔隙度，直至颗粒模型基本参数符合工程实际状态各层填土料，各步骤建立模型过程见图2。颗粒模型中所涉及的边界条件，包括水闸边界、涵洞以及地基等构件均采用刚体单元，且其与土颗粒模型的接触界面服从线性模型[16-17]。

图2 PFC建模过程

为保证计算结果准确性与合理性，在颗粒模型中建立应力场、位移场监测点，按照模型最大颗粒尺寸监测原则，所有监测点的布设见图3。A-H测点为应力场监测点，可获得涵洞上覆土层中不同高度处的土压力分布状态，顶面I测点可获得最上覆土层竖向土压力，位移测点按照A-H分布范围内均衡布设。

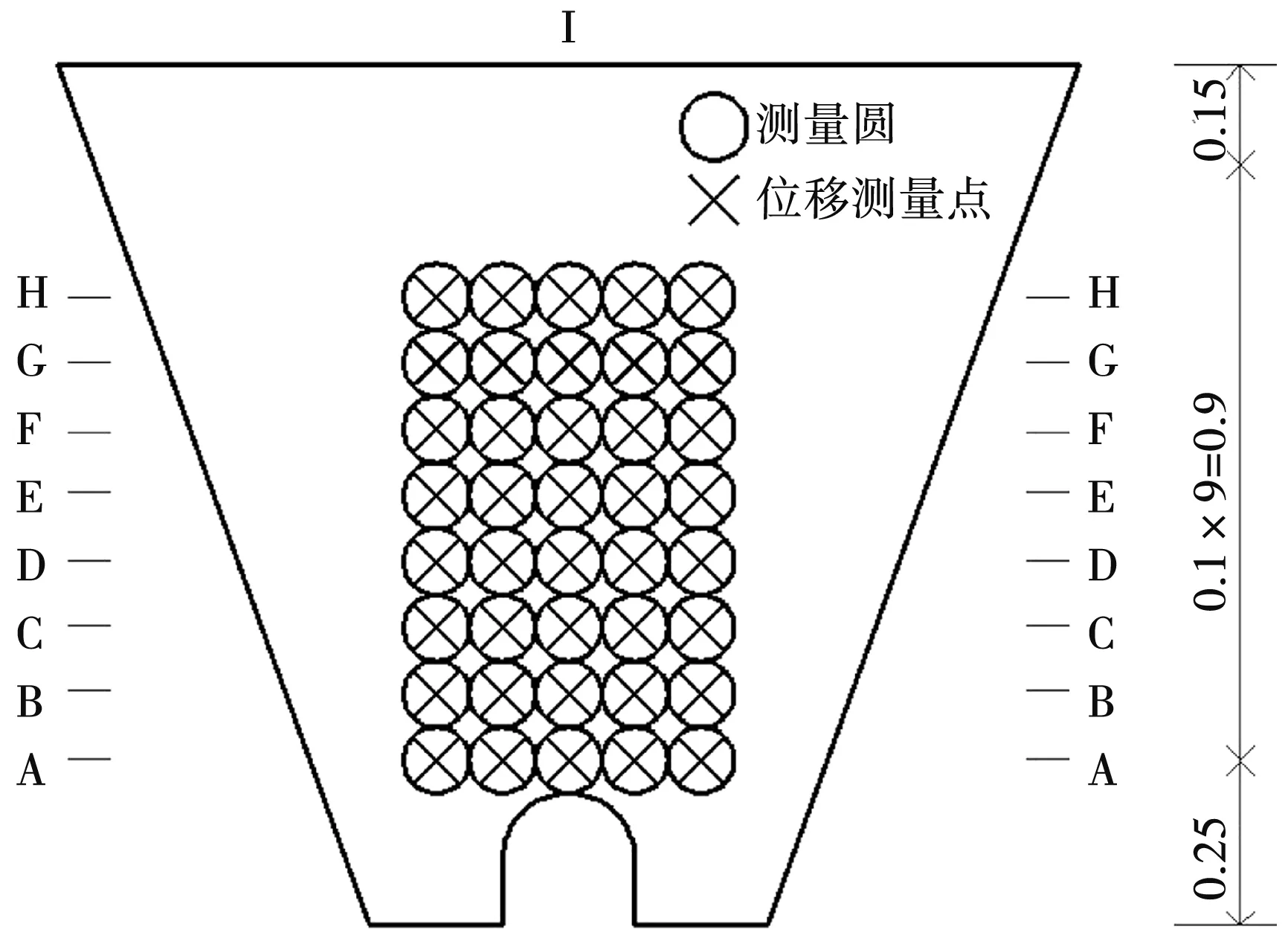
图3 应力、变形监测点布设示意图

3 涵洞上覆填土位移场特征

3.1 测点平面上位移

经离散单元法仿真求解，获得涵洞上覆填土料位移场分布特征，见图4。从图4中各测点平面上竖向位移分布曲线可知，在A-B测点平面上，竖向位移呈V形，在C测点平面后，竖向位移曲线呈倒V形，表明竖向位移在上覆填土层厚度超过C测点后发生较大逆转性变化，变化拐点对应的填土层厚度为0.59 m。从8个测点平面上竖向位移变化趋势可知，距离涵洞愈高，则竖向位移值愈大，即涵洞上覆填土层厚度与竖向位移具有正相关关系。当均处于涵洞中点时，A测点平面的竖向位移值为0.012 6 mm，而C测点、F测点、H测点平面上相应的涵洞中点竖向位移相比前者分别增大8.4倍、15.3倍和17.9倍。分析认为此与土层自重应力有关，当上覆填土层厚度递增，实质上增加了竖向荷载，为竖向位移的发展提供了“动力”，表现在竖向位移递增，本质上亦造成了涵洞受到较大沉降位移。从涵洞中点位移递增态势可发现，各个测点平面之间竖向距离为11.4 cm，当测点平面竖向距离递增11.4 cm，上覆填土层竖向位移平均递增85.9%；而从幅度递增过程中亦可知，在上覆填土层厚度增长前期，竖向位移的增长速度显著，表现在A测点-E测点平面，测点平面竖向距离递增11.4 cm，涵洞中点位移递增1.45倍；而在上覆填土层达到一定程度后，竖向位移的增长速度放缓，表现在E测点-H测点平面，测点距离增大11.4 cm，涵洞中点位移增长幅度仅为9.4%。从同一测点平面上竖向位移分布可知，涵洞两侧土体竖向位移量值均为一致性，在位移变化曲线中呈对称式分布，且涵洞两侧竖向位移在各竖向测点间幅度差异低于涵洞中点，在距离涵洞中点0.1 m处，C测点、F测点、H测点平面上相应的竖向位移相比A测点分别增大2.6倍、5.2倍和7.1倍，表明竖向位移的发展很大程度上对涵洞中点影响最大。

从不同平面位置处相对位移变化曲线可知，A测点至C测点的相对位移变化幅度可达115%，而在C测点之后，相对位移变化幅度较小，各测点间最大变化幅度仅为10%，其变化拐点与图4(a)中竖向位移分布形态变化转折点一致。从相对位移分布量值可知，C测点后相对位移均为负值，表明位移处于负方向的沉降，而在A、B测点相对位移分别为0.031和0.006 mm，均为正值，表明A、B测点处土层还并未处于显著沉降。

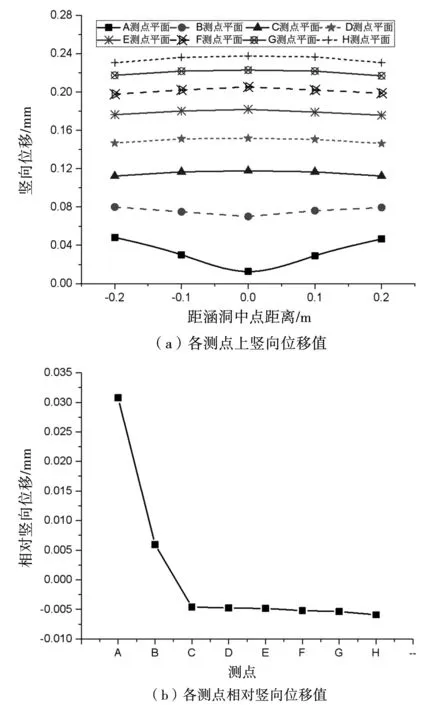
图4 上覆填土层位移特征

综上分析可知，涵洞式水闸上覆填土层厚度超过0.59 m时，位移处于向下沉降，对涵洞具有“下拱”效应。

3.2 填土高度上位移

图5为涵洞上覆填土层不同厚度下颗粒模型竖向位移分布状态。为分析方便，本文将不同填土层厚度均借助同一涵洞高度h为对比参数，分别为1.5h、2h、3h和4h。对比4个不同土层厚度下土体位移分布可知，当填土高度低于1.5h时，上覆填土层中位移分布呈W形，两侧土体的竖向位移差较大，最大竖向位移逐步靠近涵洞中点；在填土层厚度为2h时，仅在涵洞上方区域内存在W形分布，而在顶部土层中竖向位移呈U形分布，两种分布形态之间的位移差较小；当填土层厚度为3h和4h时，竖向位移分布均为U形，呈现涵洞内侧土体位移总高于两边外侧土体位移，涵洞中间土体位移较大，易发生失稳滑移。图5中黑线标注为涵洞内、外侧土体最大竖向位移相等平面高度，从等位移线发展趋势可知，其随填土层厚度递增，而逐渐降低并趋于平稳状态，填土厚度为3h和4h时，等位移线所处高度均为1h，等位移线的降低表明涵洞两外侧填土位移的发展逐步靠拢涵洞内部中点处。

图5 不同填土厚度下颗粒模型竖向位移分布

4 涵洞上覆填土应力场特征

离散单元法不仅能计算出涵洞上覆填土层中位移变化，亦可获得应力场分布特征，见图6。从图6可知，土压力以涵洞上方测点为最大，随距离涵洞上方愈大，土压力愈低，涵洞中点处A测点的土压力为19.7 kPa，而在C测点、F测点、H测点的土压力相比之降低了48.2%、78.4%和95.3%。从整体土压力分布形态可知，A-D测点间涵洞内外侧土体中土压力分布具有显著差异，以涵洞中点土压力为最大。在B测点中，两侧土压力相比涵洞中点处降低17.5%和37%；但在D-H测点中，涵洞内外侧土体中土压力基本一致，差异幅度微小；在G测点中，两外侧土体压力为2.7和2.83 kPa，与涵洞中点内侧土压力相差无几。分析表明，当填土层厚度递增，涵洞中点内侧土体产生的压应力会传递至两外侧土体内，进而表现同一侧点上涵洞内外侧土压力达到相等态势。

图6 上覆填土层应力特征

从涵洞内外侧土体相对压应力变化可知，随着填土层厚度增加，相对土压力逐渐递减至负值并达到稳定，A点相对土压力为9.4 kPa，而在G、H测点处相对土压力分别为-0.01和-0.17 kPa。这主要是由于涵洞中点内侧较大的土压力传递至外侧，造成内侧土压力低于外侧土压力，进而表现相对土压力处于负值区间。但在内外侧土体相互摩擦传递过程中，土压力会逐步过渡至稳定状态，即随着填土层厚度增大，相对土压力稳定在0 kPa左右。