基于卷积神经网络算法估算苏东沿海农作物潜在蒸散量研究
2021-09-03谭成宇
谭成宇
(江苏省东台市水利建设有限公司,江苏 盐城 224200)
江苏省是我国著名的“鱼米之乡”,而江苏省东部沿海地区是重要的农作物生产区。农作物在生长过程中将通过蒸发与腾发等方式消耗一定的水量,而作物需水量的精准估算对提高农作物产量、节约灌溉用水具有非常重要的现实意义。潜在蒸散量(ET0)的估算是确定目标区域作物需水量的基础,是灌溉排水与水资源调度工程规划与设计的前提,其精确估算对保障我国的粮食生产用水安全与水资源高效利用具有重要意义[1]。根据估算原理,ET0的估算可以分为直接法和间接法两种[2]。直接法是对ET0的历史数据本身进行统计分析并据此推演未来的ET0变化过程;间接法是基于气象数据与作用机理来计算ET0值[3]。受气候变化影响,ET0的统计规律不断演变,因此直接法的可靠性已经难以得到保障[4-6]。由于气象因子的预测水平不断提升,间接法已逐渐成为估算ET0的主流方法。
标准的ET0值通过Penman-Monteith公式来计算,理论上,可靠性最高的间接法采用Penman-Monteith公式和气象因子数据进行计算,该方法需要日最高气温、最低气温、风速、日照时长、相对湿度5项变量。一方面,许多地区缺乏详细的风速、日照时长和相对湿度数据;另一方面,目前对风速和相对湿度的预测水平尚难以满足要求。因此,该方法难以得到普遍的应用。Hargreaves模型仅需要日最高气温和最低气温2项数据,可以一定程度上弥补Penman-Monteith方法的不足,因此,目前得到了非常广泛的应用[7]。但是,Hargreaves模型忽略了很多气象因子的影响,其误差一般较高。近年来,人工智能发展迅速,该领域中的深度学习技术得到了突发猛进的发展,该技术可以自动挖掘出数据之间的作用关系与隐藏的规律,为ET0高性能估算方法的建立提供了可能。卷积神经网络深度学习算法是一种包含了卷积计算的神经网络构架,可以组合低层特征形成高层特征,可响应局部范围数据的神经元特性,具有非常好的非线性映射能力,是人工智能领域的最前沿成果之一,具有非常好的应用前景[8]。
目前基于卷积神经网络深度学习算法的潜在蒸散量估算方法的研究论文较少,本文旨在对该方法进行尝试并对其性能进行评价。基于江苏省东部地区东台、吕泗、南通和射阳4个站点1984年1月1日至2019年12月31日间的逐日最高气温、最低气温、风速、日照时长和相对湿度数据,分别采用标准的Penman-Monteith公式和Hargreaves模型计算各站点的ET0值。最后,训练出ET0的卷积神经网络模型、利用该模型计算各站点的ET0值,并与用Penman-Monteith公式和Hargreaves模型计算的结果进行对比,从而为ET0的估算工作提供新的方法和参考。
1 研究方法
1.1 研究区域与数据
研究区域为江苏省东部沿海地区,共包含东台、吕泗、南通和射阳4个气象站。东台站位于江苏省东台市,处于江苏省沿海中部、长江三角洲北翼,高程4.3m。吕泗站位于江苏省启东市,高程5.5m。南通站位于江苏省南通市,处于华东地区、江苏省东南部,高程6.1m。射阳站位于江苏省盐城市射阳县,苏北沿海中部,高程2m。苏东沿海地区的土壤主要包括山地土壤、丘陵旱地土壤、平原旱地土壤、丘陵水稻田土壤等类型,盛产粮食、棉花、油料、蚕桑等农作物,目前正在积极推进轮作换茬、冬耕晒垡、休耕培肥等轮作休耕方式,农业发展迅速。
实测气象数据包含4个气象站1984年1月1日至2019年12月31日间的逐日最高气温、最低气温、风速、日照时长和相对湿度,数据来源为中国气象科学数据共享服务网。每个站点每日包含5项数据,共13149日。
1.2 Penman-Monteith计算ET0
Penman-Monteith公式是基于物理原理的ET0计算公式,其计算的结果被公认为ET0标准值。公式为
(1)
式中:Δ为饱和水汽压-温度关系曲线斜率;Rn为冠层表面净辐射量,MJ/(m2·d);G为土壤热通量,MJ/(m2·d);γ为湿度计常数(干湿球常数),kPa/℃;T为2m高度处日平均气温,℃;U2为在地面以上2m高处的风速,m/s;es为空气饱和水汽压,kPa;ea为空气实际水汽压,kPa。
1.3 Hargreaves模型计算ET0
Hargreaves 模型仅需要日最高气温和日最低气温数据,对数据要求量远小于Penman-Monteith公式,其表达式为
(2)
式中:T为日最高气温与最低气温的平均值,℃;Rs为太阳辐射,MJ/(m2·d),其计算公式为
(3)
式中:KRs为经验系数,沿海地区其值一般设定为0.19;Tmax为日最高气温,℃;Tmin为日最低气温,℃。
1.4 卷积神经网络
卷积神经网络(CNN)是一种具有深度学习能力的神经网络,通过模仿视觉机制对原始数据进行提取,可深层次传播,降低网络复杂度,避免过拟合与欠拟合问题。CNN的基本组成结构包括输入层、卷积层、池化层、全连接层和输出层。本文最终的构架包括3层卷积层,2层全连接层。其中,第一个卷积层由32张特征图组成,第二个卷积层由64张组成,最后一个卷积层由128张组成。这些层是将输入数据以不同的方式进行特征提取,之后将它们输入全连接层,最后输出一个神经元,作为预测结果。在本项目中,集中80%的数据选择为训练数据,剩下的20%为测试数据。输入变量为日最高气温和日最低气温,输出变量为ET0值。
2 研究结果
2.1 ET0实际值时间序列
对1984年1月1日至2019年12月31日间东台站的所有数据(逐日最高气温、最低气温、风速、日照时长和相对湿度)进行整理,结果见图1(a)~图1(e)。应用这些数据,采用Penman-Monteith公式计算出ET0实际值的时间序列,结果见图1(f)。根据图1数据可知,东台市的最低ET0为0.4mm/d、最高值为8.8mm/d。对所有数据进行统计,得到各站点的统计特征值,结果汇总于表1中。根据表1可知,江苏省东部沿海地区的ET0平均值介于2.6mm/d和2.7mm/d之间,其中吕泗站与南通站略高,其他两站略低。
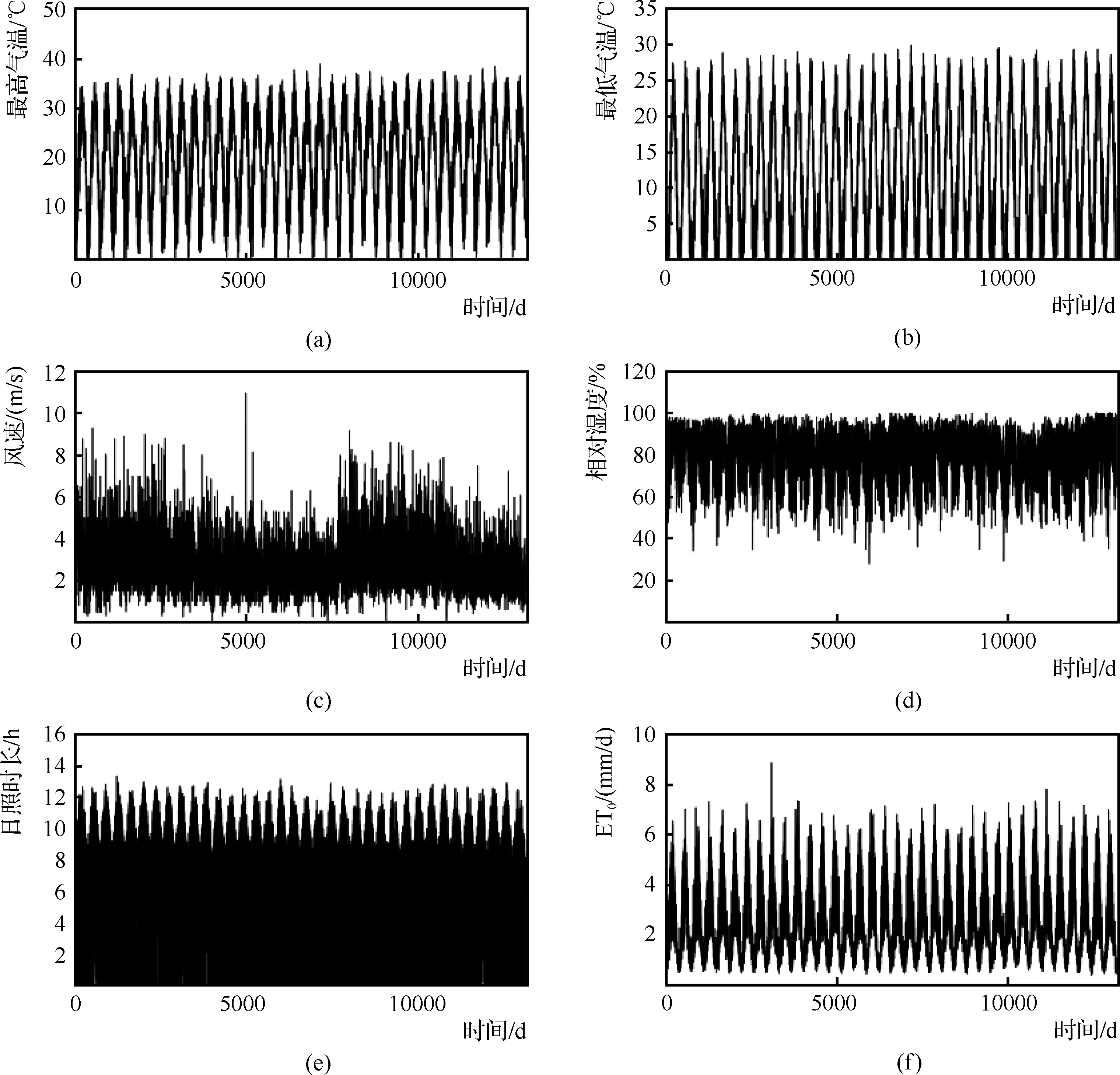
图1 东台站逐日气象数据与ET0计算结果
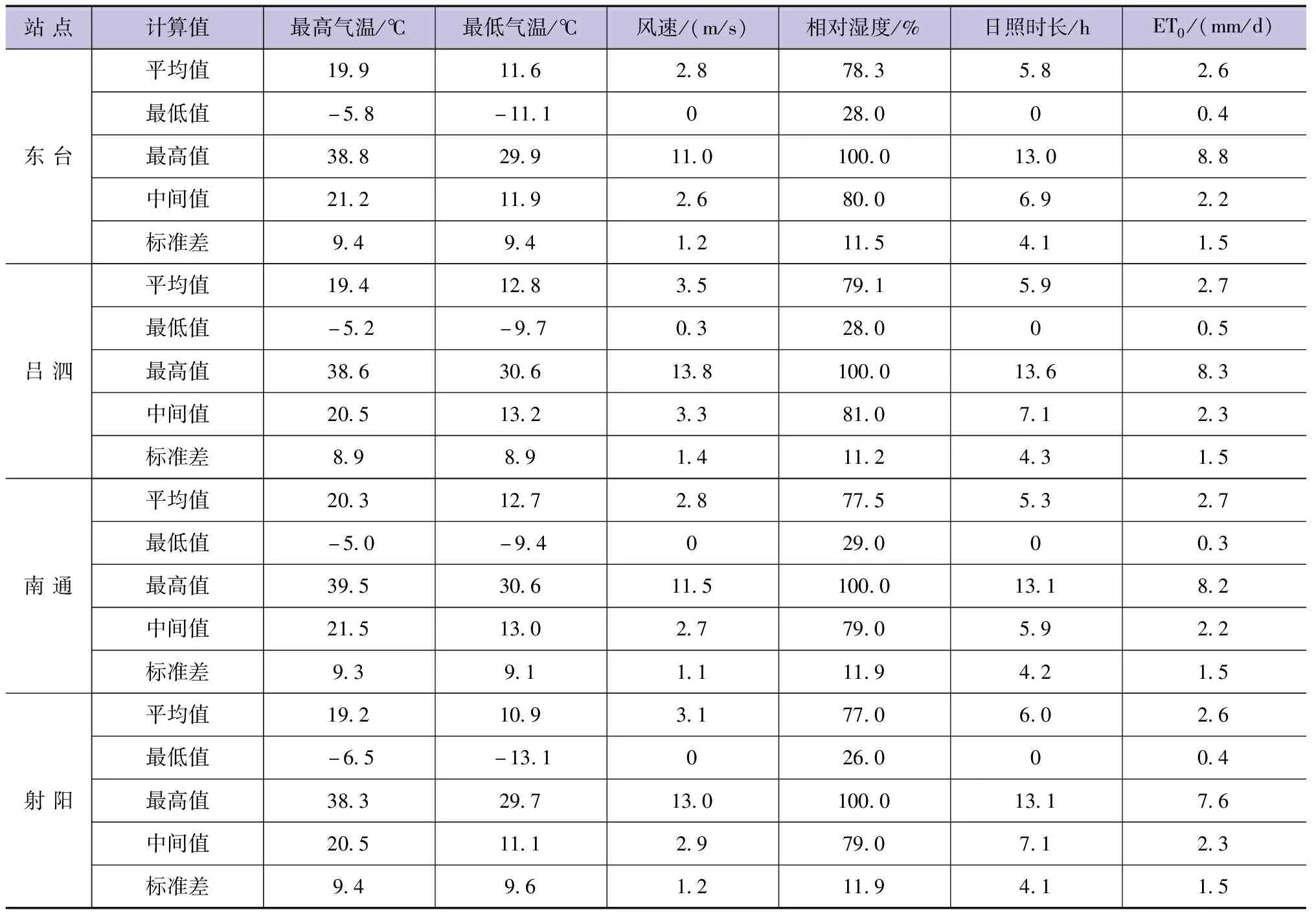
表1 4个站点逐日气象数据与ET0统计特征值对比
2.2 基于Hargreaves模型的ET0估算值
采用日最高气温和最低气温数据,基于Hargreaves模型进行各站点的ET0估算,结果见图2。东台站与南通站的ET0平均值较高,均为3.2mm/d;射阳站次之,为3.1mm/d;吕泗站最低,为2.9mm/d,估算的平均值明显高于实际平均值。东台站、吕泗站和射阳站的最小值均为0.4mm/d,南通站为0.3mm/d,与实际值较为接近。射阳站最高值最大,为8.5mm/d,明显高于实际值;吕泗站与南通站的最高值均为8.2mm/d,与实际值较为接近;东台站的最高值为8.1mm/d,明显低于实际值。东台站与南通站的中间值均为3.0mm/d,明显高于实际值;射阳与吕泗站的中间值分别为2.9mm/d和2.7mm/d,也明显高于实际值。东台、南通和射阳站的标准差均为1.7mm/d,吕泗站的为1.6mm/d,略高于实际值。
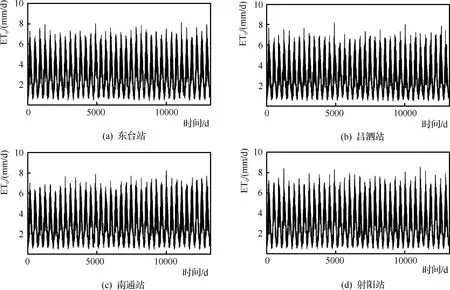
图2 基于Hargreaves模型的各站点逐日ET0计算值
2.3 基于CNN算法的ET0估算值
采用日最高气温和最低气温数据,基于训练得到的CNN模型进行各站点的ET0估算,结果见图3。东台站、南通站、射阳站的平均值为2.9mm/d,吕泗站为2.8mm/d,高于实际值,但相对于Hargreaves模型的估算结果,其高估的程度较低。吕泗站和射阳站的最小值为0.5mm/d,东台站和南通站的分别为0.4mm/d和0.3mm/d,与实际值较为接近。各站点按照最高值由高到低排序分别为射阳站、东台站、南通站和吕泗站,其值分别为7.9mm/d、7.7mm/d、7.6mm/d和7.5mm/d,除射阳站外,各站点的取值均低于实际值。东台站和南通站中间值均为2.7mm/d,射阳站和吕泗站的中间值分别为2.6mm/d和2.5mm/d,均高于实际值。东台站、南通站和射阳站的标准差均为1.6mm/d,略高于实际值,而吕泗站的为1.5mm/d,与实际值相同。
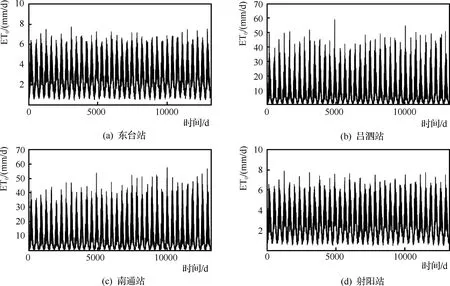
图3 基于CNN人工智能算法的各站点逐日ET0计算值
3 结果讨论
为进一步讨论估算方法的性能,将所有的数据点绘制于图4中,其中横坐标代表实际值,而纵坐标代表估算值,斜线为等值线。散点距离等值线越近则代表估算值越接近实际值,散点位于等值线左上方,说明估算值偏高,反之亦然。由图4可知,Hargreaves模型和CNN算法所对应的ET0散点较为均匀地分布于等值线两侧,说明其性能较好。但是,Hargreaves模型所对应散点的偏离程度明显高于CNN算法,说明CNN可以明显地提升ET0预测性能。计算估算值的误差指标,结果表明,Hargreaves模型的决定系数(R2)为0.79,而CNN算法的为0.93,其提升幅度约15%。Hargreaves模型估算值的均方根差(RMSE)为0.88mm/d,而CNN算法的为0.45mm/d,其误差降低幅度接近50%。Hargreaves模型的平均绝对百分误差(MAPE)为30.44%,而CNN的为15.21%。Hargreaves模型的平均绝对误差(MAE)为0.67mm/d,而CNN的为0.34mm/d。鉴于此可以认为,相对于Hargreaves模型,CNN算法可将估算误差降低约50%。CNN算法可显著提高ET0预测性能的可能原因主要有两条:CNN算法可以深度挖掘变量之间的隐藏关系,所建立的模型在内在机理方面可能比Hargreaves模型更为完善;另一方面,CNN算法建立的是数据驱动模型,相当于是进行了地区修正的模型,在研究区域内具有更好的适用性。
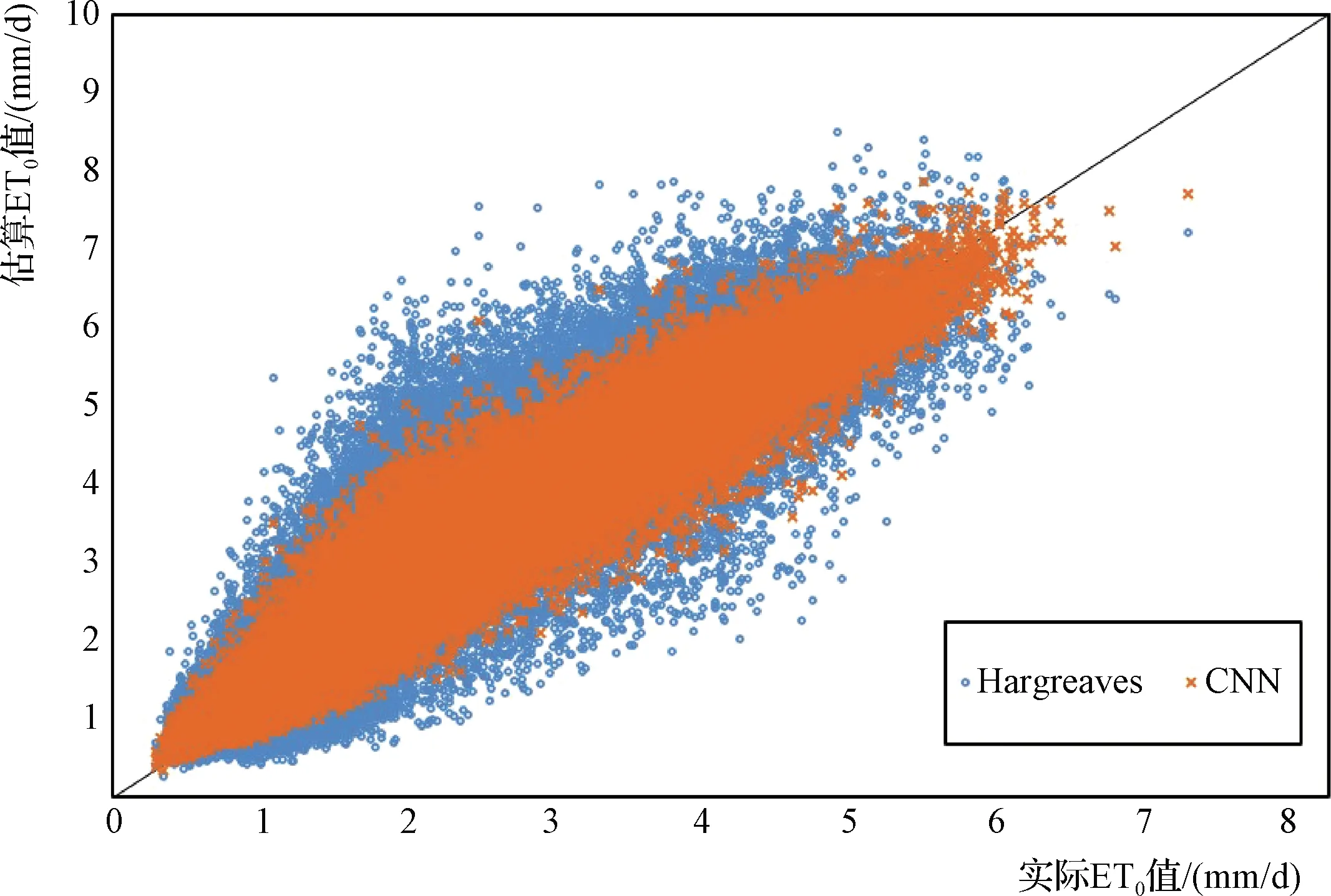
图4 ET0的实际值与估算值
4 结 语
潜在蒸散量的估算对农业种植和水资源开发与管理具有非常重要的现实意义,而苏东沿海地区为我国重要的农作物生产区,因此有必要对该地区的潜在蒸散量估算方法进行研究。本文利用26万多条的逐日气象数据,基于Penman-Monteith公式计算了江苏省东部沿海地区的逐日ET0值。分别采用Hargreaves模型和CNN算法,应用日最高气温与日最低气温数据进行了各站点逐日ET0值的计算并进行了对比。结果表明,相对于Hargreaves模型,CNN算法可以大幅度降低其估算误差,降幅接近50%。因此,采用CNN算法估算逐日ET0值具有较好的可行性。研究成果有望提高苏东沿海地区当前作物需水量的估算精准性,从而可以在保证农作物产量的同时避免水资源浪费,为当地的高标准农业建设与水资源管理工作提供科学依据。当然,数据驱动类的模型在普遍适用性方面存在一定的缺陷,因此,本文采用CNN模型估算农作物蒸散量可能仅适用于江苏省东部沿海地区。未来,有必要采用更多地区的数据对该模型进行改进与拓展,从而不断地提高其普适性。
