一个多参数优化系统在简单模型中的应用
2021-09-03祖子清杨庆夏江江张蕴斐朱学明
祖子清,杨庆,夏江江,张蕴斐,朱学明
(1.国家海洋环境预报中心自然资源部海洋灾害预报技术重点实验室,北京 100081;2.中国科学院东亚区域气候-环境重点实验室,中国科学院大气物理研究所,北京 100029)
1 引言
相对于自然界真实的大气和海洋的状态变化,数值预报总是伴随着预报误差。误差来源可分为初始误差和模式误差[1]。初始误差是因为数值模式使用了不准确的初始条件,而初始条件的准确程度会受到观测系统的空间布局以及观测仪器精度等因素的限制[2-4]。模式误差是由于数值模式对自然界真实状态演变过程的描述存在不合理之处,这取决于模式的差分方案、物理过程的参数化方案[5]以及模式使用的物理参数值等是否合理[6-7]。
对于模式误差,合理选取模式物理参数的取值,可以在一定程度上抵消模式误差[8-9]。在调整参数时常用的方法是手动调整,即给定一个参数值,然后积分模式,考察模拟是否更加靠近观测,然后根据这一信息继续更新参数值。这种方法往往运算量大,且具有主观性和片面性。因此,人们发展了多种数学方法对模式参数进行调整,如基于集合卡曼滤波的方法[10-13]、基于四维变分的方法[14-15]和基于粒子滤波的方法[16]等。
四维变分同化是一种有效的调整模式参数的方法[17-19]。该方法定义目标函数衡量同化窗口内模拟的状态变量与观测序列的距离,采用变分(伴随)方法搜索使距离缩小的方向,利用优化算法不断更新物理参数值,最终使状态变量不断趋近于观测序列。Zhang等[20]采用伴随方法和孪生试验,对三维正压潮汐模式中的二维底摩擦系数进行了优化。Peng等[21]利用伴随方法,针对风暴潮预报中较为关键的物理参数(如拖曳系数)进行了优化,结果表明通过同化观测数据,参数的调整可以抵消部分模式误差(不论这部分模式误差是否由于拖曳系数的误差所致),显著提升风暴潮增水预报能力。Zhang等[22]利用四维变分方法估算了海洋边界层模式中的两个参数。但是,这种方法的缺点是优化系统设计复杂、需要数值模式具备伴随模式、可移植性差。
本文发展了一个多参数优化系统。该系统设计简单,便于移植,采用直接计算梯度的方法,不需要数值模式事先具有伴随模式,适用于数值模式中少量参数(少于10个)的优化问题。在孪生试验的假定下,本文基于一个理想的模型,开展了3个参数的优化试验。本文首先介绍使用的模型和方法,然后介绍试验结果,最后进行总结和讨论。
2 模型和方法
2.1 模型简介
本研究使用了盒子模型进行参数估计。盒子模型是为研究北大西洋经圈翻转环流的稳定性和多平衡态等性质而发展的一个模型[23-25]。盒子模型较为简单,包括两个方程,3个物理参数,没有空间格点,方程如下:
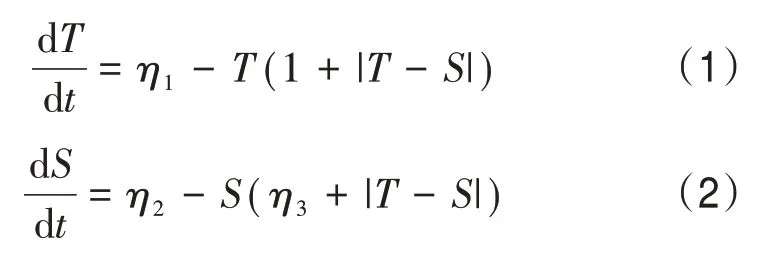
式中:T和S分别为海盆南北两侧的温度和盐度之差;η1和η2分别代表南北两侧的热力和淡水强迫之差,η3为温盐对大气强迫松弛时间的比值。式(1)和式(2)中所有变量均为无量纲量。在数值离散时采用了二阶龙格库塔方案。时间步长取Δt=0.001。
在积分过程中,各时刻的状态变量Fi=(Ti,Si)是初始条件(T0,S0)和参数(η1,η2,η3)的函数Fi=Fi(T0,S0;η1,η2,η3),即状态变量会随着初始条件和参数取值的变化而改变。给定η1=3.0,η2=1.02,η3=0.2(将这组参数值分别记为ηb1,ηb2,ηb3),当初始条件取为T0=1.875,S0=1.275时,系统处于平衡态,即此时状态变量Ti和Si在积分过程中不随时间变化。为了孤立物理参数变化对状态变量变化的影响,本文所有试验的初始条件均取为T0=1.875,S0=1.275。因此,在积分过程中,模型状态的变化可完全归因于参数值的变化。
2.2 方法简介
本研究的试验设计采用了孪生试验的假定。首先,假定参数真值为。在真值的设定下,积分模型3 000步,且从第500步开始,每隔200步取一对T和S作为观测值(To和So)。然后,建立多参数优化系统,将上述观测同化进系统中。同化系统会根据模型的状态变量与观测数据的距离及其梯度等信息,对模型参数进行多次修正,使模型的状态变量不断逼近观测。最后,当模型的状态变量与观测的距离达到极小值时,获得最优参数,或称最优参数增量,此时需要考察最优参数值能否从最初的(ηb1,ηb2,ηb3)收敛 到 参 数 真 值,或 者 最 优 参 数 增 量(Δη1,Δη2,Δη3)能否从随机数收敛到参数的增量真值(0.02,-0.03,-0.04)。
在多参数优化系统中,为了衡量模型状态变量与观测数据的距离,引入了如下的目标函数:

式中:Ti和Si为状态变量,为参数增量的函数,即Ti=Ti(Δη1,Δη2,Δη3)和和为观测数据,为常量。时间频次i由观测数据确定,从第500个时间步开始,间隔200步取一次,共13个(N=13)。实际上,目标函数即为状态变量相对于观测的均方根误差。
参数估计过程中的关键问题在于如何计算梯度,即目标函数对参数增量的梯度(∂J/∂Δηi,i=1,2,3)。在四维变分同化中,计算梯度需要用到伴随模式,算法也较为复杂。考虑到盒子模型的参数较少,模型简单,且积分时间较短,本文采用直接计算梯度的方法。计算目标函数相对于参数增量Δηi的梯度,需分别在ηbi+Δηi和ηbi+Δηi+ε下积分模型,获得对应的状态变量F(ηbi+Δηi)和F(ηbi+Δηi+ε),并计算状态变量与观测的距离J(ηbi+Δηi)和J(ηbi+Δηi+ε)。目标函数相对于该参数增量Δηi的梯度即为:
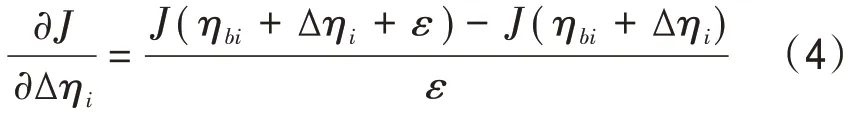
式中:ε为小值,取1.0×10-7。需要说明的是,这种计算方法获得的梯度精度要高于伴随(变分)方法的精度,但缺点是每增加一个参数的梯度,需要单独运行一次模式。
多参数优化系统的优化算法使用了序列二次规划(Sequential Quadratic Programming,SQP)算法[26-27],该方法适用于非线性系统的等式和不等式约束规划问题。理论上讲,在参数估计的问题中,不应该设置参数增量(Δη1,Δη2,Δη3)的范围约束,即参数增量的优化问题是一个无约束的问题。但是考虑到SQP算法的要求,此处将参数增量的范围设置为[-10,10],远远大于参数真值的变化范围(0.02,-0.03,-0.04)。如果在参数增量优化过程中达到了给定的范围边界,则需将范围进一步扩大。
综上,多参数优化系统的计算流程如图1所示。(1)首先,系统产生随机数,作为参数增量Δηi的初猜值;(2)将参数增量Δηi叠加到参数基态ηbi上,作为参数值,积分盒子模型,获得状态变量的时间序列F(ηbi+Δηi);(3)基于观测数据和状态变量的时间序列,计算目标函数J(ηbi+Δηi);(4)在参数基态和参数增量(ηbi+Δηi)的基础上,再叠加一个小扰动ε,并积分盒子模型,获得状态变量的时间序列F(ηbi+Δηi+ε);(5)基于观测数据和状态变量的时间序列,计算目标函数J(ηbi+Δηi+ε);(6)计算目标函数相对于参数增量的梯度∂J(ηbi+Δηi)/∂Δηi;(7)将 目 标 函 数J(ηbi+Δηi)和 梯 度∂J(ηbi+Δηi)/∂Δηi输入优化算法,更新参数增量Δηi;(8)重复过程(2)—(7),直到优化算法达到终止条件;(9)多次重复过程(1)—(8),从目标函数的极小值中找出最小值,并将对应的参数增量作为全局最优的参数增量。在这个流程中,目标函数衡量当前参数设置下模型的状态变量与观测之间的距离,梯度提供距离在当前参数增量的一个小邻域内的导数信息。优化算法基于目标函数与梯度,不断调整参数值,使状态变量不断逼近观测数据,获得最优的参数增量。

图1 多参数优化系统的计算流程示意图
在手动调整模式参数时,人们经常每次只调整1个参数值,在此过程中其他参数值是固定的。调整好1个参数的取值之后,再去调整第2个参数。这种做法是否存在局限性呢?本文设计了两组试验,一组同时优化3个参数,另一组分别单独优化3个参数,用以考察单独优化参数时,是否可以找到当前参数的真值。在两组试验中,梯度的计算方案稍有差别。同时优化3个参数时,相当于在点(ηb1+Δη1,ηb2+Δη2,ηb3+Δη3)的邻域内计算梯度,如式(5)—(7)所示。单独优化1个参数时,相当于在点(ηb1+Δη1,ηb2,ηb3),(ηb1,ηb2+Δη2,ηb3)和(ηb1,ηb2,ηb3+Δη3)的邻域内分别计算梯度,如式(8)—(10)所示。

3 结果
3.1 同时优化3个参数
将随机数作为参数增量的初猜值,基于状态变量和观测的距离及其梯度信息,多参数优化系统同时对3个参数增量进行了优化,优化的结果如图2和表1所示。
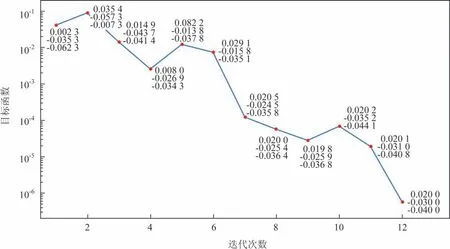
图2 同时优化3个参数时,目标函数和参数增量的变化(红色点表示损失函数值,右侧的3个数值从上往下依次表示Δη1、Δη2、Δη3的值)

表1 3个参数的增量真值、最优值及其对应的目标函数
优化系统从随机数开始,经过了12次迭代,收敛到参数增量真值(0.02,-0.03,-0.04)。最优参数增量的误差量级分别为10-7、10-4和10-4。目标函数(均方根误差)调整前为2.11×10-2,调整后下降到5.7×10-7。从状态变量上看(见图3a—b),调整前参数为基态ηb1,ηb2,ηb3,模型处于平衡态,状态变量不随时间变化(蓝色线),与观测数据相差较远。调整后,状态变量(红色线)逼近所有观测数据。这说明,多参数优化系统可以根据观测数据和多次模型积分结果,找到参数增量真值。

图3 观测和模型状态变量随积分步数的变化
在每次迭代中,模型需要计算F(ηb1+Δη1,ηb2+Δη2,ηb3+Δη3),F(ηb1+Δη1+ε,ηb2+Δη2,ηb3+Δη3),F(ηb1+Δη1,ηb2+Δη2+ε,ηb3+Δη3),F(ηb1+Δη1,ηb2+Δη2,ηb3+Δη3+ε),需积分模型4次,12次迭代共需积分48次。如果给定3个参数增量的搜索半径[-0.1,0.1],那么采用遍历搜索半径内每个参数增量的方法,为达到上述参数估计的精度,则需要积分模型2×106×2×103×2×103=8×1012次。如此大的运算量,对于简单的盒子模型都是不可行的,对于复杂的大气海洋环流模式更是无法实现。这也从另一个角度说明,多参数优化系统在很大程度上降低了模型的积分次数,这在需要较长积分时间的复杂环流模式的参数优化问题中,是尤为有用的。
图2所示的初猜值符号恰好与增量真值的符号相同,这在一定程度上有助于优化过程的收敛。如果初猜值的符号与真值增量不同,则可能会增加迭代的次数,优化过程可能不收敛于真值增量。然而,在实际情况下,我们无法事先知道真值增量的符号。因此,采用多组随机初猜值,重复图1所示的优化过程,是十分必要的。
3.2 单独优化3个参数
对参数进行手动调整时,人们往往每次只调整1个参数,然后评估该参数对模式模拟的改进程度。将该参数调整到最优之后,再调整下一个参数。从上文的讨论中,这相当于在(ηb1+Δη1,ηb2,ηb3)的邻域内搜索梯度的下降方向和最优参数增量,而不是在(ηb1+Δη1,ηb2+Δη2,ηb3+Δη3)的邻域内搜索。对于多个参数均存在误差的情况下,这种方法是否能收敛到3个参数的增量真值?本文设计了另一组试验,分别单独优化3个参数增量,考察是否可以得到相应的参数增量真值。
计算结果如表1中试验2.1—2.3所示。单独优化Δη1,最优参数增量为-0.043,与增量真值0.02相差较多,目标函数调整前为0.021,调整后下降到0.013。最优参数增量不仅数值上与增量真值相差较多,且符号相反,这说明参数调整的方向是错误的。从图3b中可以发现,调整后S与观测差别较小,但T与观测差别较大,甚至较调整之前更大。
单独优化Δη2时,最优参数增量为0.016,与增量真值-0.03差别较大,且符号相反,目标函数调整前为0.021,调整后下降到0.003 6。最优参数增量与增量真值符号相反,说明Δη2调整的方向也是错误的。相对Δη1而言,Δη2优化之后,目标函数下降较多。从图3c可以发现,优化后的T和S距离观测相对较近,但效果与同时优化3个参数的情形仍存在较大的差别。
单独优化Δη3时,最优增量为-0.013,与真值增量相差相对较小,符号相同,目标函数调整前为0.021,调整后下降到0.003 6。相对于Δη1和Δη2,Δη3的最优增量符号与增量真值相同,说明参数调整的方向是正确的。从图3d可以发现,调整参数后的状态变量趋近于观测数据,但效果仍与同时调整3个参数的情形存在一定差异。
以上的试验结果说明,如果每次只调整1个参数,可能会导致单个参数的调整方向错误。在这个错误的基础上,继续调整第2个参数,必然会导致第2个参数的值出现错误。在一组错误的最优参数增量设置下,目标函数不可能达到全局最小值。因此,每次只调整一个参数是存在局限的。
4 总结和讨论
对于数值模式中少量参数的优化问题,本文建立了一个多参数优化系统,可以对数值模式的多个参数进行同时优化,以减小模式的系统性偏差。该系统设计简单、易于维护和进一步扩展;系统与数值模式采用文件进行数据交换,因此便于移植到其他数值模式上。
本文将多参数优化系统与一个简单的盒子模型结合,检验了参数优化的效果。首先,基于孪生试验,预先给定盒子模型的参数真值,并产生观测数据。然后利用该系统对模型的3个参数同时进行优化。结果显示,优化算法经过约10次迭代后,系统可以找到预先给定的参数真值。另外,分别单独优化3个参数时,虽然状态变量也趋近了观测,但程度有限;参数增量并不收敛于给定的参数增量真值,甚至会出现最优参数增量与参数增量真值反号的情况。这说明,当人们采用手动方法对模式参数进行逐一、单参数调整时,参数调整的效果具有一定的局限性,而同时调整多个参数可以降低这种局限性。
在实际中,对于复杂的大气和海洋环流模式,我们无法事先判断哪些参数是存在误差的,同时对于大量的参数,限于运算量也无法同时进行调整。从实用的角度讲,只要能降低误差,参数调整就是有意义的,即参数调整无需收敛于真值,而是尽可能大地抵消模式误差,使模式状态变量最大程度上趋近于观测[21]。在这种前提下,同时优化尽可能多的参数,相对于较少的参数,往往可以在更大程度上使状态变量趋近于观测。
多参数优化系统具有较好的可移植性。首先,系统采用了直接计算梯度的方式,避免使用复杂的四维变分同化计算方案,尤其是避免了调用伴随模式。这在很大程度上简化了系统的复杂性,同时对于目前尚不具备伴随模式的数值模式(比如多数生态模式和风暴潮增水模式)也可以方便地进行移植。虽然使用直接计算梯度的方式会在一定程度上增加积分模式的次数(每增加1个参数需要多积分模式1次),但是如果同时优化的参数个数少于10个,这种方案的运算量依然是可以接受的。其次,多参数优化系统通过数据文件与模式进行数据交换。系统将模式参数增量值写入模式的参数文件,模式积分完成后,系统再读取积分结果,并计算目标函数。在这个流程中,模式积分作为一个独立的模块嵌入到系统中,保证了系统可以方便地移植到其他数值模式上。
多参数优化系统是为调整大气和海洋环流,以及海洋生态等复杂模式中的多个参数设计的,本文是将其应用到简单模型的一次尝试和检验。在复杂模式中应用该系统需要考虑更多的因素。比如,复杂模式中参数众多,需要挑选少量重要的参数进行调整,这依赖于一定的参数调整经验。如果海洋模式中,温度的垂向廓线误差较大,那么首先需要调整温度发展方程中的扩散系数。根据经验确定了少量重要参数之后,需要对这些参数取值进行扰动,考察这些参数取值的变化是否的确可以引起模式状态的显著变化。在复杂模式中,目标函数需要根据关注的问题确定。如果海洋的垂向温度模拟误差较大,观测数据选择了Argo温度廓线,那么目标函数可以选择模式温度的均方根误差。此时,参数调整的目标就是降低模式温度的误差。另外,复杂模式中不同参数间的取值范围不同,需要进行归一化以促进优化算法收敛等。目前,针对南海业务化海洋学预报系统使用的ROMS(Regional Ocean Modeling System)模式,我们已经利用多参数优化系统对其中的5个物理参数同时进行了调整,结果显示,多个模式变量的模拟得到了显著的改善,我们将会在另一篇文章中讨论这些问题。
