基于水电站闸室不同试验分组下扰动试验测定值对比探析
2021-09-03林兰兰
林兰兰
(营口奕东水利勘测设计有限公司,辽宁 营口 115000)
0 前 言
水电站闸室钢梁受荷载影响较大,荷载越大水电站闸室钢梁扰动特征越明显[1]。因此在进行水电站闸室设计时,需要对钢梁的扰动特征进行分析,从而设计最大能承受的荷载,保障水电站的安全运行[2]。当前,对于水电站闸室钢梁扰动特征主要采用反复荷载的计算方法进行探讨[3-10],但该方法需要进行钢梁扰动参数的设置,其参数设置也是反复荷载计算的难点所在,有一些学者主要通过物理模型方式在一些钢梁结构扰动特征进行分析,但在水利工程方面应用还较少,为此文章基于物理模型对水电站闸室钢梁扰动特征进行分析,并探讨该方式对其扰动参数的影响。研究成果对于水电站闸室稳定性设计具有重要参考意义。
1 研究方法
采用物理模型方法对水电站闸室钢梁梁扰屈服度进行计算,其计算方程为:
(1)
式中:My为钢梁扰动受力,kPa;H0为钢梁扰动横向荷载间距,m。刚体屈服度计算时,需对其变形位移进行计算,其计算方程为:
△y,M=△fy+△sy+△vy
(2)
式中:△fy、△sy、△vy分别为不同受力情况下的屈服变形量,mm。
钢梁扰动屈服时的变形量计算方程为:
(3)
钢梁梁扰滑动变形位移的计算方程为:
(4)
水闸的刚体弹性变形量的计算方程为:
(5)
式中:Φ为钢梁扰动屈服变形率,mm;fy为钢梁滑变形程度;fc为水电站闸室刚体之间的轴心间距的抗荷载强度,kPa;db为钢梁扰动变动直径,mm;fy为屈服滑动变形程度;σ为钢体之间的截面应力,kPa;Ag为刚体截面面积,cm2;G为刚体剪切的弹性模量;My为钢梁扰动受力,kPa。对水电站闸室刚体扰动的峰值荷载点进行计算,其方程为:
(6)
式中:Tmax为水电站闸室刚体剪切面受到的荷载最大值,kPa;n为刚体轴向压缩系数;λ为剪切程度比例系数;ρsh为水闸闸室刚体捆扎比例,g/cm3。水电站闸室钢梁扰动的剪切度破坏特征点方程为:
(7)
3 水电闸室钢梁扰动特征分析
3.1 钢梁扰动试验指标
基于物理模型试验方法,辽宁地区某水电站闸室为具体工程实例,对其闸室钢梁扰动进行试验指标进行分析,水电站闸室钢梁扰动试验指标,见表1;水电站闸室钢梁强度试验指标,见表2。
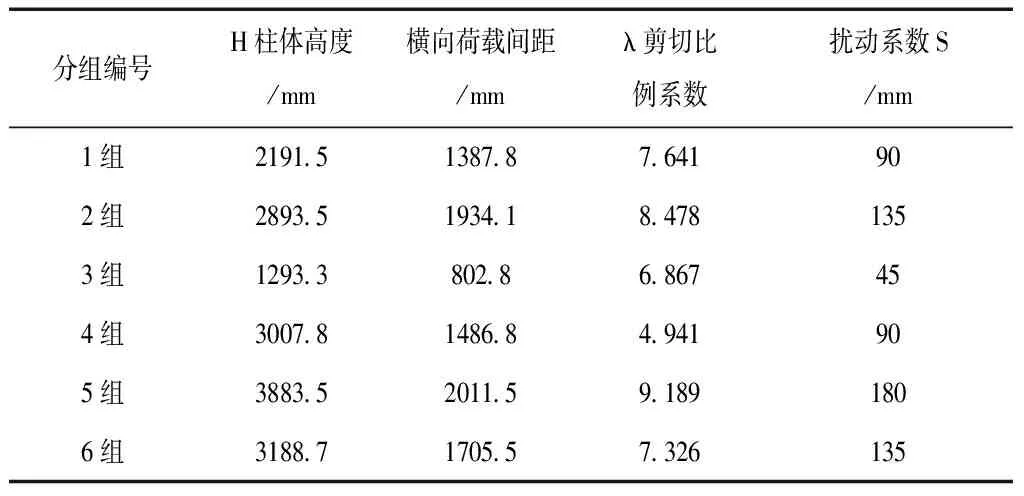
表1 水电站闸室钢梁扰动试验指标
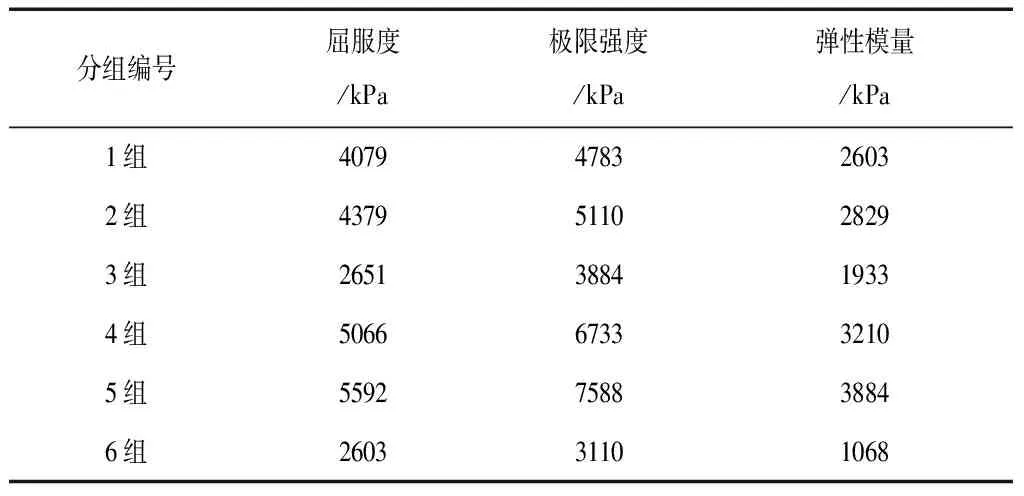
表2 水电站闸室钢梁强度试验指标
3.2 扰动特征值计算对比
对不同试验分组下水电站闸室的钢梁扰动计算值进行差异对比,不同试验分组下扰动试验测定值和理论计算值差异对比结果,见表3。
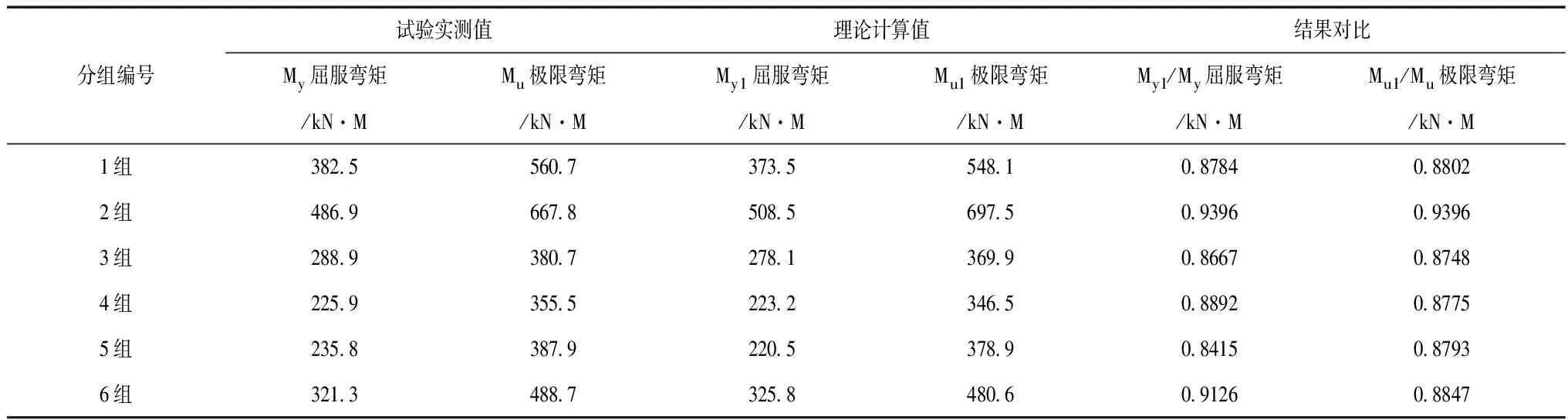
表3 不同试验分组下扰动试验测定值和理论计算值差异对比结果
从不同试验分组下扰动试验测定值和理论计算值差异对比结果可看出,水电站闸室扰动特征试验测定的屈服弯矩以及极限弯矩和理论计算值具有较好的吻合度,表明物理模型试验结果较为合理。在具体水电站闸室工程设计时,可综合采用钢梁扰动的理论方程和物理模型进行综合对比,确定其扰动的特征点。
3.3 钢梁扰动孔隙特征试验分析
采用物理模型试验方法对不同荷载条件下水电站闸室钢梁扰动的孔隙特征进行试验分析,不同荷载条件下水电站闸室钢梁扰动的孔隙特征试验结果,见表4。
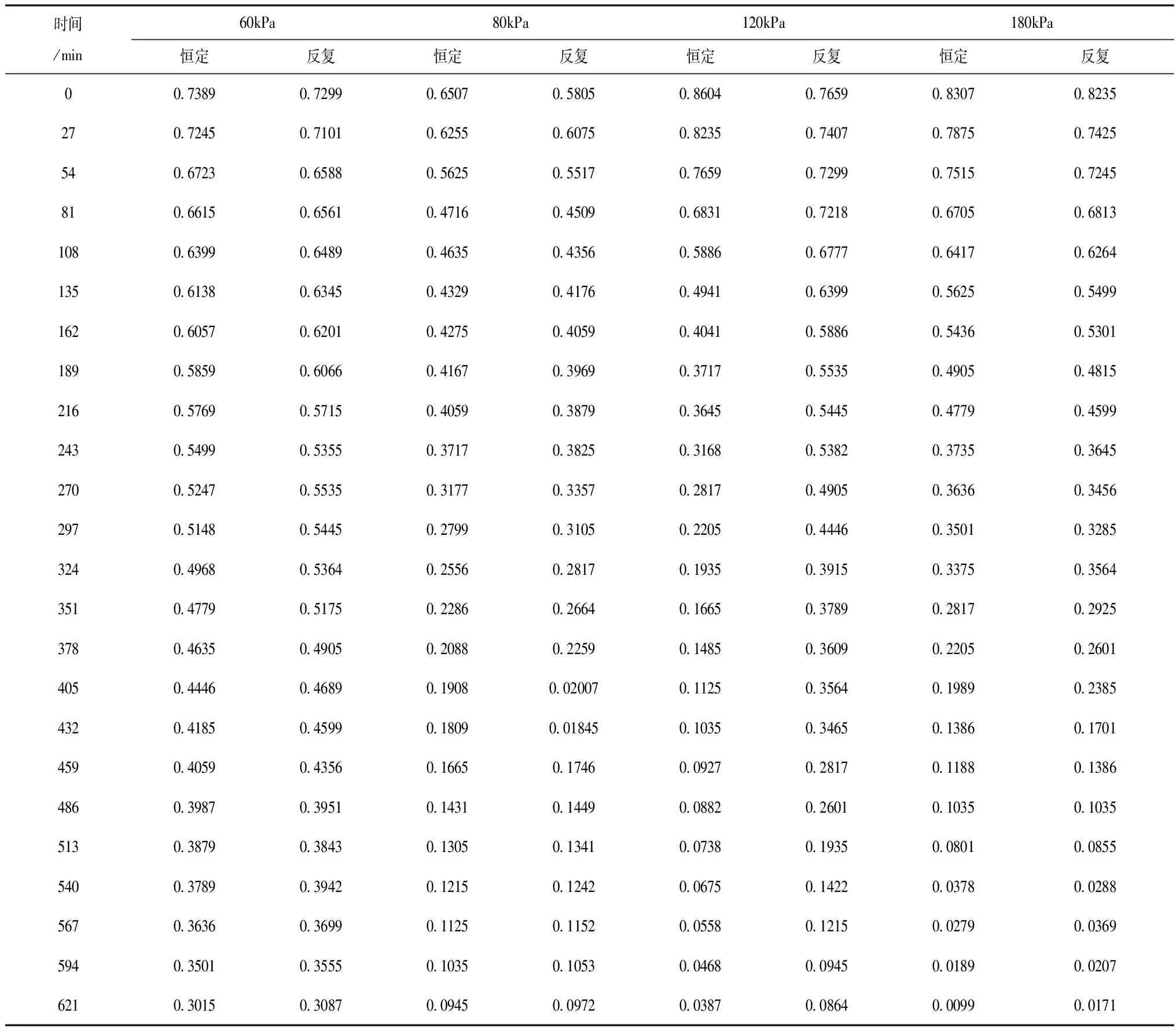
表4 不同荷载条件下水电站闸室钢梁扰动的孔隙特征试验结果
从不同荷载条件下水电站闸室钢梁扰动的孔隙特征试验结果可看出,水电站闸室钢梁扰动孔隙比随着不同荷载的增加而逐步加大,这主要是因为钢梁扰动梯度影响了其孔隙比的变化,钢梁扰动梯度增加使得不同荷载条件下的孔隙比增幅较大。当荷载从54kpa递增到216kPa后,其不同荷载条件下的水电闸室钢梁扰动孔隙不逐步提高,均匀荷载条件下的孔隙变化幅度低于反复荷载条件下的孔隙比变化幅度[11-13]。
3.4 不同荷载条件下钢梁扰动强度试验
结合物理模型试验对各个组件的反复荷载下设计水闸闸室钢梁扰动的特征点进行试验分析,不同荷载条件下水电站闸室钢梁扰动强度试验结果,见表5。
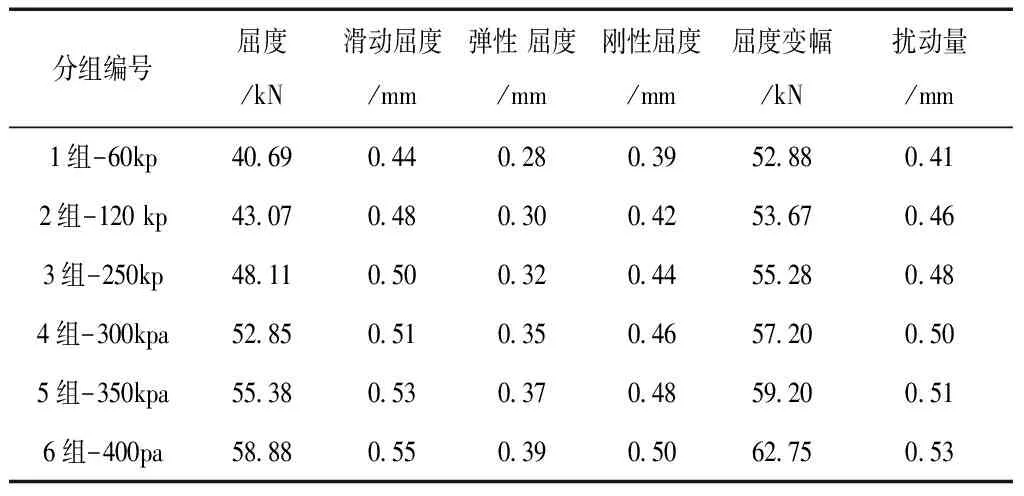
表5 不同荷载条件下水电站闸室钢梁扰动强度试验结果
从不同荷载条件下水电站闸室钢梁扰动强度试验结果可看出,水电站闸室钢梁屈度随着荷载的增加而逐步提升,但递增幅度有所下降,这主要是受到钢梁扰动荷载反复影响所致,各试验荷载条件下水电站闸室的扰动变化范围较为接近,钢梁扰动效应受反复荷载影响有所减小,钢梁扰动变化幅度随着荷载增加而有所下降。
3.5 不同荷载条件下钢梁扰动抗剪切试验
对不同荷载条件下的水电站闸室扰动抗剪切特征进行试验分析,不同荷载条件下水电站闸室抗剪试验结果,见表6。

表6 不同荷载条件下水电站闸室抗剪试验结果
从不同荷载条件下水电站闸室抗剪试验结果可看出,水电站闸室钢梁扰动损伤系数随着循环次数递增而有所减小,这表明随着荷载加载次数的提高,其不同荷载条件下的钢梁扰动效应降低。水电站闸室钢梁扰动随着荷载加大而抗剪切能力也相应降低。
4 结 语
1)在具体水电站闸室工程设计时,可综合采用钢梁扰动的理论方程和物理模型进行综合对比,确定其扰动的特征点。
2)水电站闸室钢梁扰动孔隙比随着不同荷载的增加而逐步加大,这主要是因为钢梁扰动梯度影响了其孔隙比的变化,钢梁扰动梯度增加使得不同荷载条件下的孔隙比增幅较大。
3)水电站闸室钢梁屈度随着荷载的增加而逐步提升,但递增幅度有所下降,这主要是受到钢梁扰动荷载反复影响所致,各试验荷载条件下水电站闸室的扰动变化范围较为接近,钢梁扰动效应受反复荷载影响有所减小,钢梁扰动变化幅度随着荷载增加而有所下降。
