无砟轨道无缝线路钢轨碎弯影响因素分析
2021-09-03展旭和张涛金泰木罗俊王开云
展旭和 张涛, 金泰木 罗俊 王开云
1.国家高速列车青岛技术创新中心,山东青岛266111;2.西南交通大学牵引动力国家重点实验室,成都610031
无砟轨道的扣件系统直接与混凝土道床连接,一般认为其轨道稳定性较好,不易发生失稳。现场观测结果表明,无砟轨道虽不会发生胀轨跑道现象,但钢轨可能以碎弯的形式危害行车安全。遂渝线无砟轨道试验段曾出现过钢轨碎弯现象[1],中国铁道科学研究院在2007年调查嘉陵江大桥、蒋家大桥、木鱼山隧道口等地段的轨向和轨距时,测得三处钢轨碎弯,轨距偏差分别为2.0、-2.5、-2.0 mm,对应的碎弯波长均为4 m,分析碎弯地段的脱轨系数和轮重减载率得出线路存在潜在安全隐患。可见无砟轨道无缝线路稳定性问题是不容回避的,这也是无砟轨道应用带给无缝线路技术的新问题[2]。文献[3]认为钢轨纵向温度力、钢轨初始弯曲和线路横向阻力是影响轨条臌曲的主要因素。本文从以上三方面继续深入探讨和研究,分析钢轨碎弯影响因素及作用规律,为提高无砟轨道平顺性、保证行车安全提供理论支撑。
1 有限元模型及参数
运用ANSYS有限元软件建立CRTSⅠ型双块式无砟轨道三维有限元模型(图1),分析在轨条纵向力作用下钢轨初始弯曲和扣件横向刚度对钢轨碎弯的影响及作用规律。计算参数见表1。
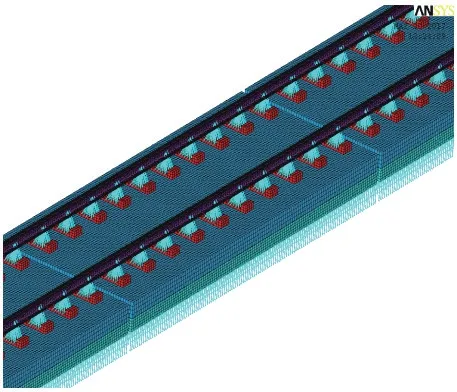
图1 CRTSⅠ型双块式无砟轨道有限元模型

表1 CRTSⅠ型双块式无砟轨道计算参数
2 钢轨等效升温幅值
线路存在初始弯曲情况下,钢轨在较大纵向力的作用下将发生臌曲变形。随着我国客运专线的兴建,长大跨度桥梁应用越来越广泛[4],桥上钢轨还须承受来自梁轨相互作用产生的伸缩附加力。文献[5]将最大伸缩附加压力转化为相应的升温幅值施加于钢轨上,这样使计算结果偏于保守。此外,现场实测资料显示[6-9],无缝线路在运营之后普遍存在锁定轨温下降的现象,这样钢轨承受的纵向力会更大,出现钢轨碎弯的概率也会提高。综合考虑上述影响因素,建议将最大伸缩附加压力转化为钢轨等效升温幅值ΔTeq,其表达式为
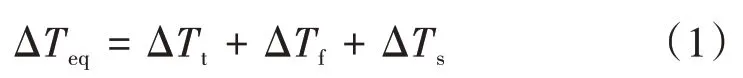
式中:ΔTt、ΔTf、ΔTs分别表示温度作用产生的升温幅值、伸缩附加力换算的升温幅值、无缝线路锁定轨温的下降值。
2.1 ΔT t的确定
一般情况下,由温度作用产生的升温幅值ΔTt可按照TB 10015—2012《铁路无缝线路设计规范》[10],取当地最高气温加20℃再减去钢轨锁定轨温;特殊情况下,应对当地气温资料作补充调查,统计分析后确定合理的取值。
2.2 ΔT f的计算
伸缩附加力换算的升温幅值ΔTf取值的决定性因素包括桥梁温差和温度跨度。为研究桥梁温差和温度跨度对ΔTf的影响,以连续混凝土桥为研究对象,建立梁轨相互作用模型[11],其中ΔTf的计算表达式为
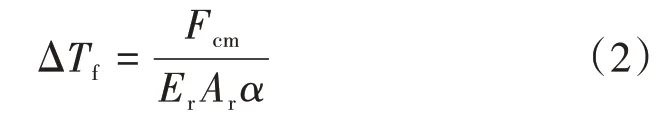
式中:Fcm为钢轨最大附加压力;Er为钢轨弹性模量;Ar为钢轨截面面积;α为钢轨线膨胀系数。
不同桥梁温差Tb和温度跨度Lt下的ΔTf计算结果见图2。可知:当桥梁温差一定时,ΔTf随着温度跨度增加而线性增加,且桥梁温差越大其线性增长速率越快;当温度跨度一定时,ΔTf随着桥梁温差的增加而增加,且桥梁温差大于20℃时,其增幅逐渐变小。
2.3 ΔT s的确定
对于无缝线路,钢轨蠕变伸长会引起长轨条锁定轨温下降,影响无缝线路稳定性。使钢轨产生蠕变伸长的原因很多,大致可分为以下几类:①制造时钢轨中产生的残余应力在使用过程中发生分布变化而改变钢轨长度;②钢轨受温度拉力作用而产生蠕变伸长;③钢轨受到列车长期碾压、冲击作用而塑性碾长等。根据文献[6-9]调研结果,线路锁定轨温普遍存在3~10℃的下降。
在武广客运专线铺设双块式无砟轨道的桥梁中,未设钢轨伸缩调节器的王灌冲特大桥温度跨度达195 m[12]。参考图2可知,当梁体升温取30℃时,其伸缩附加力转化的升温幅值为23℃。考虑温度作用的升温幅值40℃和锁定轨温下降5℃,钢轨等效升温幅值近似取ΔTeq=70℃。此外,考虑道床板受气温变化影响较大,其日温差一般不小于混凝土桥梁日温差,参考TB 10015—2012,道床板温差取30℃。
3 钢轨初始弯曲
3.1 初始弯曲线形
若钢轨存在初始弯曲,积聚在钢轨内部的温度力会向着势能低处发生能量转移,形成碎弯。假设钢轨存在三种初始不平顺线形[3,5],即线形1、线形2、线形3(复曲线),其数学表达依次为
式中:f和L分别为初始弯曲的波幅和波长。
分别计算三种线形在不同波幅和波长组合条件下引起的钢轨横向变形最大值,计算结果见图3。可知:①与线形1和线形2相比,线形3会使线路产生更大的横向变形。②线形3最不利波长为3 m,不利波长区段为2~5 m;线形1、线形2最不利波长为1 m,不利波长区段为0.5~1.5 m。③波长超过最不利波长后,钢轨横向变形逐渐减小,最后趋于平稳;且对于某一固定波长,钢轨横向变形均随着波幅增加而线性增加。由此可见,应特别重视对线路短波初始弯曲的治理,使线路初始弯曲避开或远离不利波长区段。
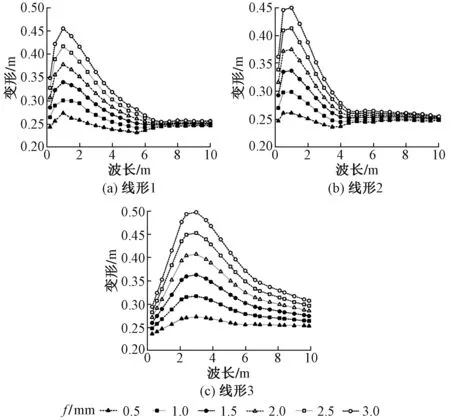
图3 钢轨横向变形最大值与波长、波幅的关系曲线
3.2 初始弯曲半波数
若初始不平顺线形为正弦曲线(线形2),其连续半波数为n=1~10(其中n=1为半波正弦),波幅f=1 mm,波长L=1、2、3、4、8、10 m。在承受等效升温幅值作用下引起的钢轨横向位移变化见图4。
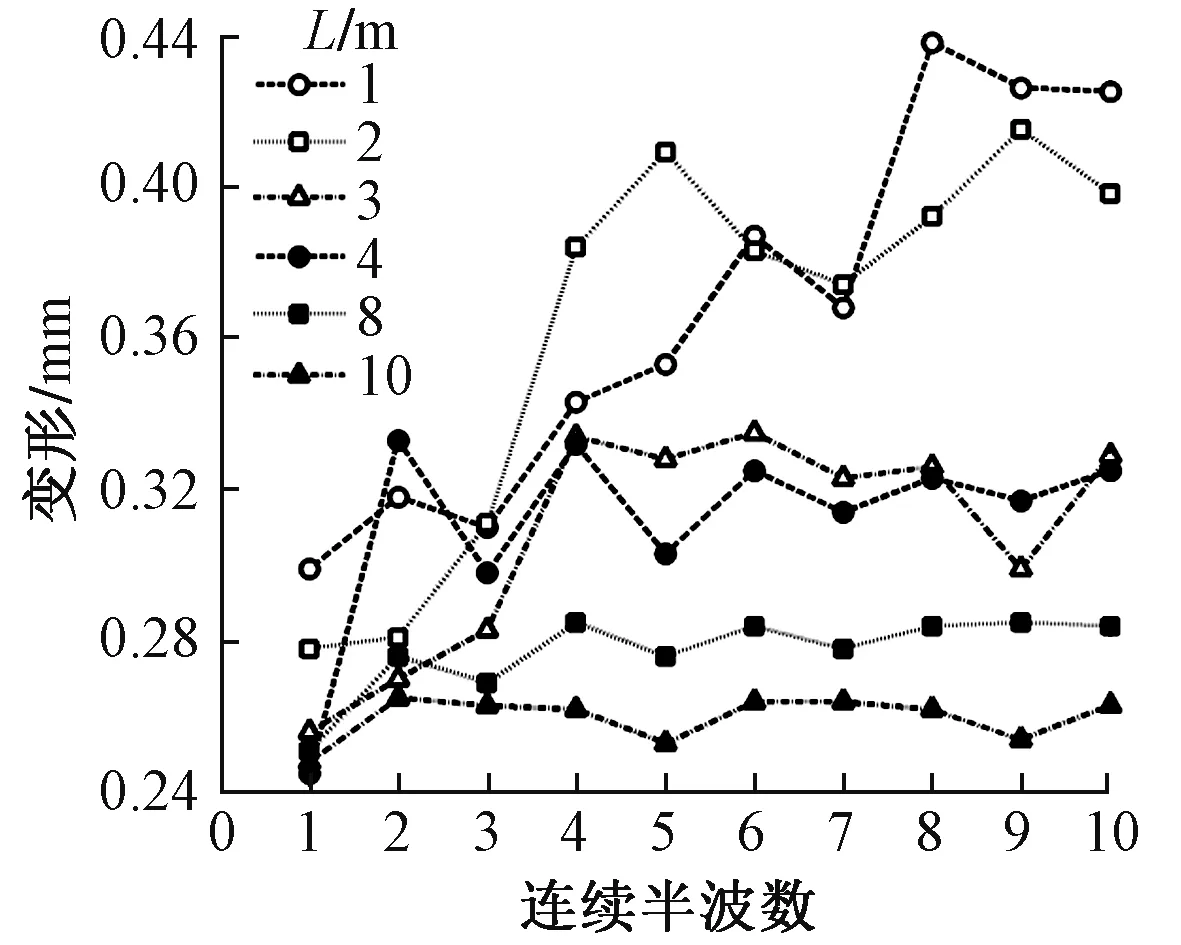
图4 钢轨横向变形最大值与连续半波数的关系曲线
由图4可知:①当初始弯曲波长取1~4 m时,钢轨横向变形最大值随着半波数的增加而显著提高;当波长为8、10 m时,增幅相对平缓。②随着连续半波数从1持续变化至10,波长L=1、2、3、4、8、10 m下钢轨横向位移增幅最大值分别为46%、49%、31%、36%、14%和7%。可见,连续短波初始弯曲易导致线路出现更大的钢轨横向位移。
4 扣件横向刚度
在长期列车荷载作用下扣件将发生扣压力损失,引起横向刚度减小,不利于线路稳定。现场无法测得单个扣件节点的横向刚度,但容易测得扣件扭矩。因此,若能建立扣件扭矩与横向刚度的关系,则可获得现场扣件横向刚度的分布情况,为钢轨碎弯理论计算提供参数依据。
4.1 扣件横向刚度分布
对某高速铁路300组WJ-8型扣件扭矩大小进行测试,发现扣件扭矩M服从均值为189.7 N·m、标准差为33.8 N·m的正态分布,即M~N(189.7,33.82),见图5。
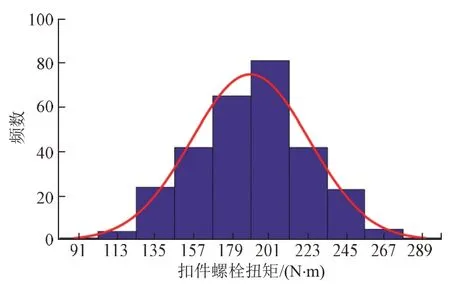
图5 扣件扭矩频数分布
文献[13]针对WJ-8型扣件测试了其在不同螺栓扭矩下的横向刚度,并对试验结果进行拟合,得出扣件横向刚度kh(单位:kN/mm)与扭矩M((单位:N·m)满足如下线性关系:
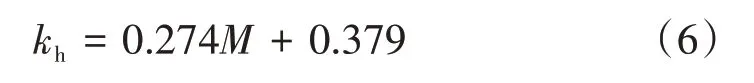
由概率论相关知识推导得kh~N(52.4,8.92)。这说明扣件横向刚度服从均值为52.4 kN/mm、标准差为8.9 kN/mm的正态分布。为方便后续计算和比较参数的差异,扣件横向度取50 kN/mm,标准差取9 kN/mm,变异系数取0.18。
4.2 扣件横向刚度不均匀分布下的钢轨碎弯
为模拟实际线路扣件横向刚度不均匀分布对钢轨碎弯变形的影响,采用Monte Carlo法进行拉丁超立方抽样,选取扣件横向刚度为随机变量。以线形3作为钢轨初始弯曲,波长和波幅分别取3 m和1 mm,左右股钢轨扣件刚度分别为kL和kR,且kL~N(50,92),kR~N(50,92)。初始弯曲平行布置于左右两股钢轨上,保证初始轨距偏差和轨距变化率均为0。
通过1 000次抽样计算获得了轨距偏差最大值和轨距变化率最大值,同时与线路扣件横向刚度普遍损失80%(以50 kN/mm为标准)的极端条件进行对比,见图6。可知:①对于初始状态满足轨道静态几何尺寸容许偏差管理值的线路,在钢轨纵向力、钢轨初始弯曲及扣件横向刚度不均匀分布的共同作用下,轨距偏差最大值为0.51 mm,小于1 mm的限值,但普遍大于确定性分析中线路横向刚度取10 kN/mm的轨距偏差。②1 000次抽样计算中,11.3%的样本轨距变化率超过限值;在扣件横向刚度均损失80%的情况下,轨距变化率未超过规范限值。
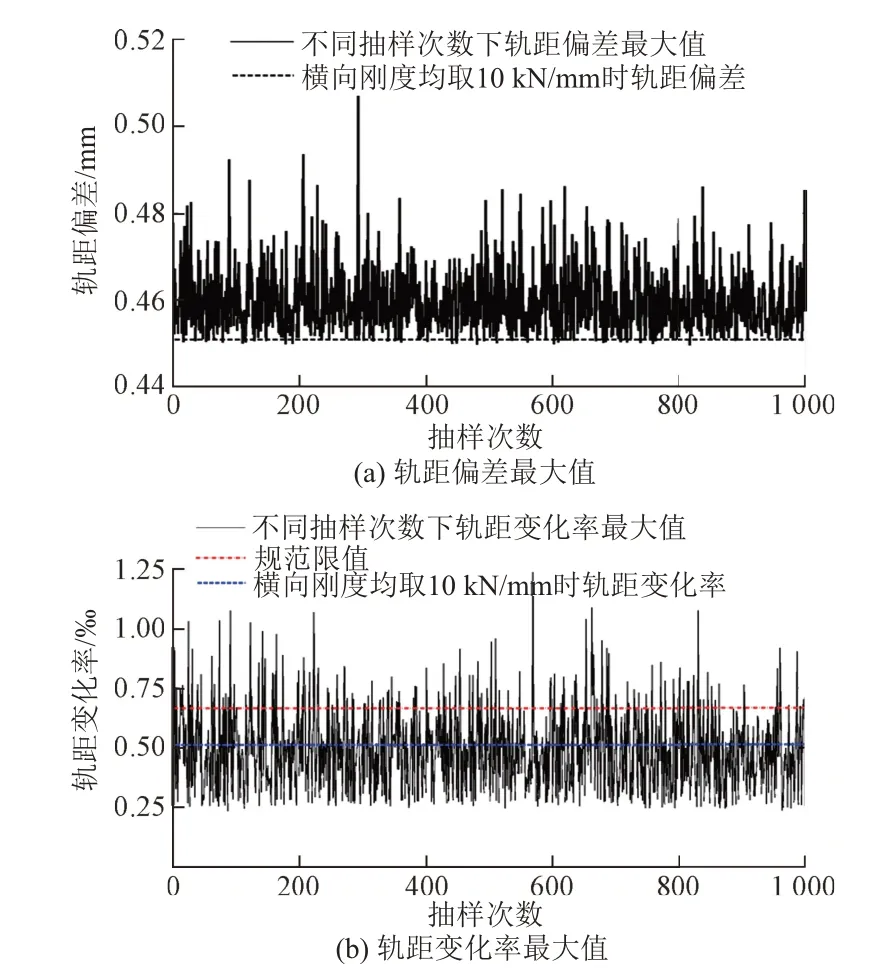
图6 轨距偏差和轨距变化率最大值
从Monte Carlo法抽样计算的结果中选取了三组使轨距变化率超限的扣件横向刚度样本,其左右股钢轨扣件横向刚度相较于50 kN/mm的变化情况见图7。其中编号为3~7的扣件之间设置了钢轨初始弯曲。
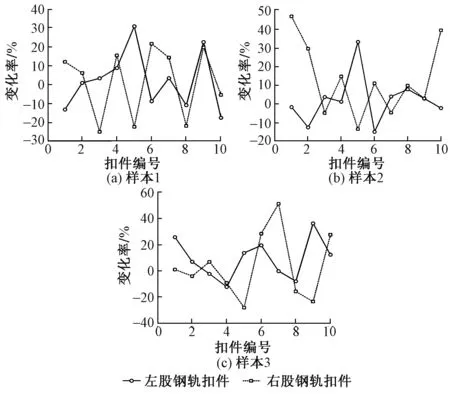
图7 轨距变化率超限的扣件横向刚度样本分布
由图7可知,三个样本中扣件横向刚度损失均不大,最大值为28%,但相邻或者相对位扣件存在40%以上的横向刚度差异。这表明,本算例中轨距变化率的超限并非由于扣件横向刚度普遍损失较多,部分扣件工作状态不良以及扣件之间较大的横向刚度差异是造成轨距变化率超限的重要原因。因此,不仅要防止扣件扣压力的损失,还应重视其分布的离散程度,以保持扣件具有稳定、正常的横向阻力。
5 结论
本文通过建立CRTSⅠ型双块式无砟轨道有限元模型,考虑等效升温幅值引起的钢轨纵向力,系统地分析了钢轨碎弯影响因素及作用规律,得到如下结论:
1)复曲线形初始弯曲会使钢轨产生更大横向变形,且不同初始弯曲线形均存在最不利波长,应尽量使线路避开或远离不利波长区段。
2)相较于单波正弦曲线,连续短波初始弯曲更易导致线路出现更大的钢轨横向位移。对线路方向严格控制的同时,应加强对连续短波初始弯曲的治理。
3)养护维修过程中不仅要防止扣件扣压力损失过多,还应避免扣件横向刚度不均匀分布造成的线路几何形位的超限,保持扣件具有稳定、正常的横向阻力。
