基于雷达海杂波的蒸发波导GA-PSO算法

2021-09-03周文静邢孟女

兵器装备工程学报 2021年8期

张瑜，周文静，邢孟女

(河南师范大学物理与电子工程学院，河南新乡 453007)

1 引言

海上大气环境中经常会出现大气波导现象，是由于海面水汽蒸发、海洋边界层大气的温度和湿度随高度急剧变化造成的[1]。蒸发波导属于一种特殊的表面波导，容易影响无线电波传播[2]。蒸发波导主要发生在海面40 m以下的范围内，出现的概率可达80%，因此加强蒸发波导的研究对提高雷达探测精度及雷达整体性能具有非常重要的战略意义[3]。

早期蒸发波导的研究出现了波导模理论、几何光学理论和抛物方程方法等基础理论。在这些理论基础上，深入研究气象条件对大气环境下电波传播的影响，例如湍流、散射等现象对电磁波传播方向和距离的影响。通过利用海面上的一些气象水文因素，如风速、位温、比湿，建立波导模型可以得到大气波导的剖面。美国的Paulus-Jeske提出了PJ模型，用不随气压变化的位折射率替代折射率N，利用总体理查森数判断大气稳定度来计算不同稳定度条件下的蒸发波导高度[4-5]。法国的研究者依据莫宁-奥布霍夫相似理论提出了MGB模型，可以对稳定和不稳定情况进行迭代解析，该模型根据大气折射率与气压、温度、水汽压的关系，比湿与水汽压的关系，位温和气温的关系，采用Geleyn方法建立模型[6]。美国学者Babin通过研究海洋大气边界层物理过程描述模型，把饱和水汽压公式融入其中；将相似理论用到低风速环境并确定相似理论中的参数，由此得到计算海面蒸发波导高度的模型[7]。美国的Naval Surface Warfare Center在弗吉尼亚Wallops岛进行实验研究[8]，发现雷达回波的变化与大气折射率的变化有关，利用雷达海杂波数据对大气波导参数进行反演，可实时提供蒸发波导信息[9]。在这之后的诸多研究都是基于该实验展开的，如遗传算法[10]、滤波算法[11]、蚁群算法[12]、免疫算法[13-14]、粒子群算法[15]等相继被用于计算反演模型。海军工程大学的左雷也曾将整体理查森数Rib引入蒸发波导剖面模型，利用不同Rib求出不同的折射率剖面[16]。

由于雷达接收的海杂波和蒸发波导参数之间的关系为非线性，因此在这些利用雷达海杂波反演蒸发波导的大多数方法中，其反演精度受到了很大的限制。为此，本文利用增加约束条件的手段来提高反演精度，提出了一种基于不同天线高度、多波段雷达频率的多目标遗传—粒子群(GA-PSO)混合算法，以期望得到高精度和高稳定性的反演结果。

2 基于雷达海杂波的蒸发波导反演方法

2.1 雷达海杂波功率计算模型

蒸发波导模型在雷达海杂波反演过程中起着非常重要的作用，通常采用大气修正折射率M进行大气波导环境分析。假设理想状态大气和海面温度不变，则修正折射率与观测高度之间的关系式为

(1)

该模型将蒸发波导厚度d作为特征参数，因其与实际情况吻合度高而应用广泛。其中z为高度；z0为波导底层高度，取值1.5×10-4；M0为距海面z0处的大气折射率，取值340。

根据建立的蒸发波导参数模型，可利用雷达方程得到雷达海杂波功率的函数表达式为

Pc(m,r)=-2L(m,r)+10log10r+σ0+C

(2)

Pc是关于大气波导特征参数m的函数式，这里的大气波导参数即为蒸发波导厚度d。其中r为雷达到海面的距离；C为与雷达系统参数有关的常数；σ0为海杂波散射系数，由雷达海杂波估计模型GIT求得。

理论研究表明[17]：影响接收雷达海杂波功率的因素有很多，如雷达频率、雷达增益、天线架设高度、极化方式、海况等，其中影响最大且可控的因素是雷达频率和天线架设高度。在蒸发波导高度较低时，高的雷达频率具有较好的反演精度；反之，蒸发波导高度较高时，低的雷达频率具有较好的反演精度。另外，不同的雷达天线高度含有不同的海杂波特征信息，它与反演精度之间并非单调变化影响，在雷达频率一定时，总存在某一天线高度使得反演误差最小。

2.2 目标函数的建立

目标函数可用来判断实测海杂波回波功率和建模仿真所得海杂波回波功率之间的符合程度。在利用海杂波反演蒸发波导时，当雷达的频率和天线高度固定时，可建立单目标函数[18]。这种情况下，由于雷达的频率和蒸发波导高度很难达到匹配状态，因此反演得到的蒸发波导的精度较差。为了提高反演精度，采用变化雷达频率的方法，即采用多波段雷达频率测量海杂波来反演蒸发波导，建立多目标函数。这样就可以在蒸发波导高度未知的情况下，减小雷达频率造成的误差，提高反演精度。另外，在雷达多频率探测的基础上，采用调节天线高度获得丰富的海杂波特征信息，进一步提高反演精度。

蒸发波导环境下，雷达海杂波反演大气折射率剖面的实现步骤如下：

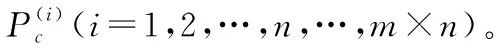
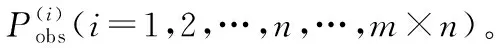
3) 建立关于实测杂波功率和建模所得杂波功率库之间的目标函数，这里采用均方误差和线性加权来描述目标函数。表达式为

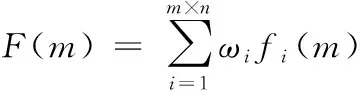
(3)

(4)

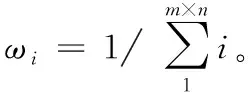
本文选取频率个数为2，f1=10 GHz，f2=12 GHz，天线高度个数为3，h1=10 m，h2=20 m，h3=30 m。不同的频率与不同的天线高度相结合会影响反演精度，可通过各种组合对单目标函数与多目标函数进行误差分析。

2.3 利用GA-PSO混合算法求解目标函数

GA-PSO混合算法是将遗传算法与粒子群算法进行结合，既留下了遗传算法的全局搜索优势，还加入了粒子群的种群信息和位置转移能力。

多目标GA-PSO混合算法是将多波段频率和多个天线高度组成的目标函数作为反演对象，采用遗传-粒子群混合算法进行反演，可求得目标函数取得最小值时所对应的蒸发波导高度。多目标GA-PSO混合算法将遗传算法嵌入到粒子群的位置和速度迭代更新中，先进行遗传算法优化，得到一组搜索值后再进行粒子群算法优化，通过设置位置参数，来选择实际需要搜索的数据范围。该算法全局搜索能力强，反演结果精确度高，稳定性好。

混合算法主要需要3个算子：提高算子、选择交叉算子、变异算子。在遗传算法中个体被看作染色体，在粒子群算法中个体被当作粒子，群体中优秀个体被选拔出来组成一个新群体，另外一部分则被淘汰掉；新群体经过选择交叉后留下子代优秀个体，最终经过变异算子后的子代和优秀个体组成的新群体进行下一代的选拔。

适应度函数即为评价函数，是遗传算法中个体是否优秀的评判标准。多目标GA-PSO混合算法保留了遗传算法这一特点，需要确定适应度函数，对群体中的所有个体进行适应度比较。由于在任何情况下适应度函数都应是非负值，本文所建立的目标函数F(x)满足该要求，将其倒数作为适应度函数进行算法反演，以便得到目标函数最小值。

算法的实现流程如图1所示。

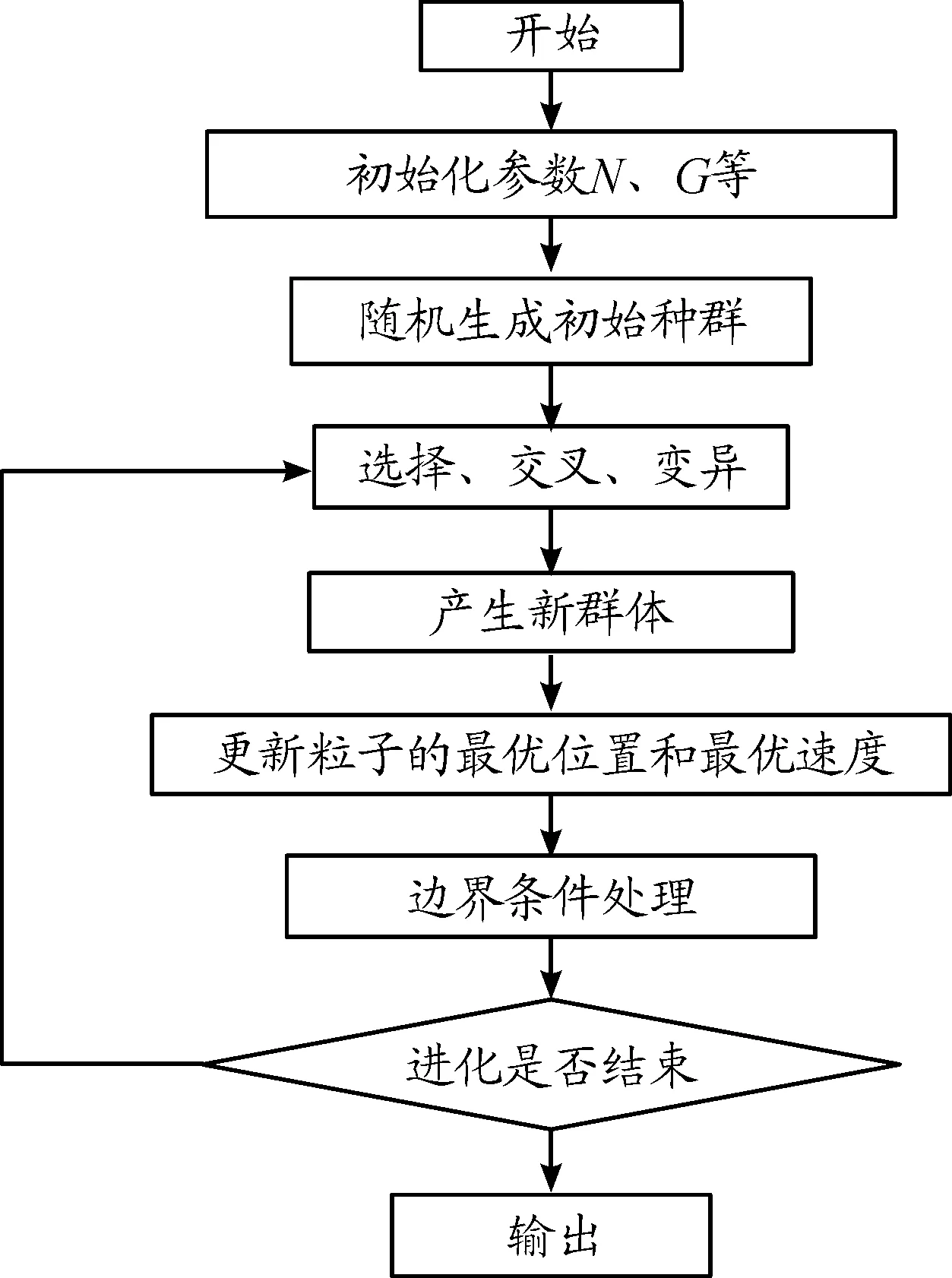
图1 多目标GA-PSO算法流程框图

多目标GA-PSO混合算法的具体操作步骤如下：

1) 初始化种群个数N，迭代次数G，惯性权重，学习因子，设置位置参数范围和速度范围。

2)随机生成粒子的初始位置x(i)和速度v(i)，设置适应度函数。

3) 引入遗传算法，依次进行选择、交叉、变异。

4) 计算局部最优值和全局最优值，留下最优个体的位置和速度。

5) 边界条件处理。

6) 循环步骤3)、4)、5)，最后输出最优解。

3 仿真结果分析

本文通过仿真实验分析来验证多波段且可调节天线高度的雷达系统利用多目标GA-PSO混合算法可以对蒸发波导反演精度产生影响。实验设置初始种群个数N=50，反演代数G=30，计算机配置为4 GB内存，CPU主频2.60 GHz，雷达环境参数如表1所示。

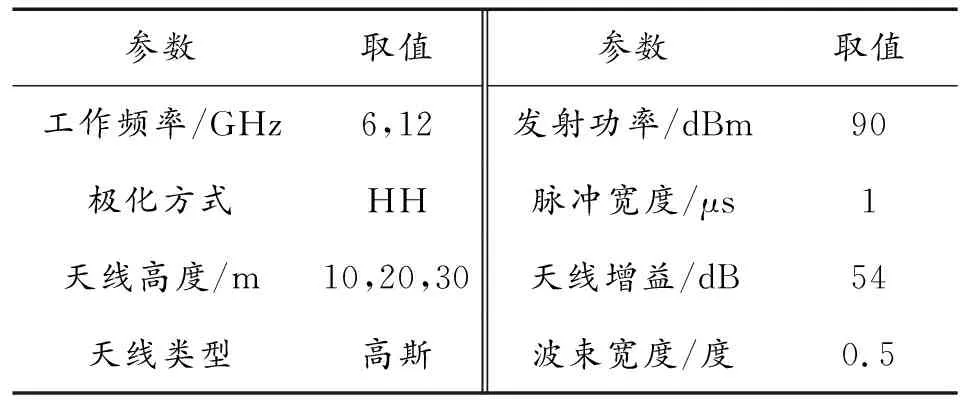
表1 雷达环境参数

在假定蒸发波导高度d为15 m、20 m两种情况下进行模拟仿真实验。图2和图3分别给出了仿真实验所得蒸发波导高度d为15 m、20 m时目标函数值随进化代数变化的优化曲线。两图从上到下分别为天线高度h1、h2、h3和可调节高度(h1,h2,h3)，从左到右分别为雷达频率f1、f2和两组合频率(f1,f2)，可以看出随着反演代数的增加，目标函数逐渐寻得最小值。

图2 波导高度为15 m，不同频率、天线高度下的目标函数优化曲线

目标函数均方误差值如表2所示。由表2可见：在波导高度为d=15 m时，当雷达频率为f1=10 GHz、天线高度为h2=20 m，雷达频率为双频率(f1,f2)、天线高度为可调节这2种情况下，目标函数均方误差值都很小。在波导高度为d=20 m时，只有雷达频率为f2=12 GHz、天线高度为可调节情况，其目标函数均方误差值很小。综合2种波导高度环境，双雷达频率(f1,f2)、天线高度可调节情况下的目标函数均方误差值都较小。

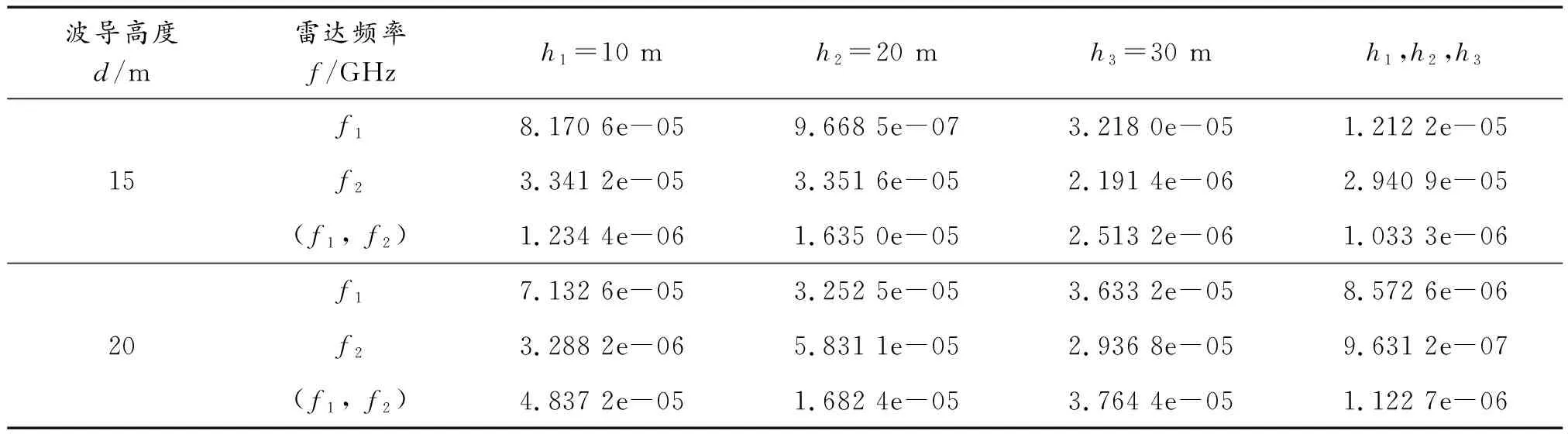
表2 目标函数均方误差值

在假定波导高度分别为15 m、20 m时，反演所得蒸发波导高度以及其相对误差如表3所示。

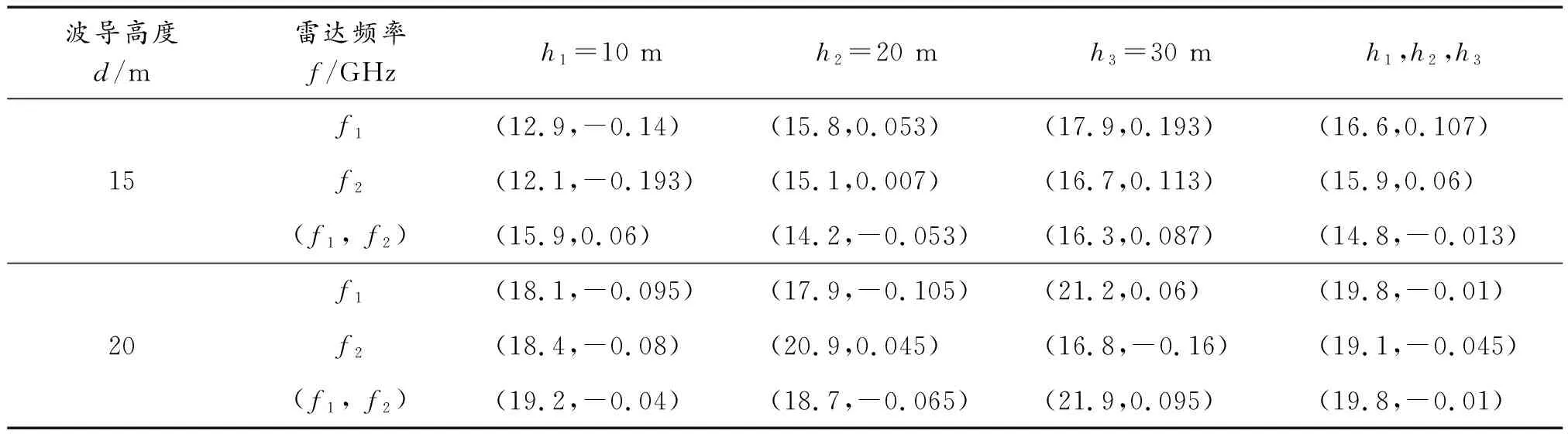
表3 蒸发波导反演高度与其相对误差

由表3中数据可得：在波导高度为d=15 m时，只有频率f1=12 GHz、天线高度h2=20 m的反演蒸发波导高度误差比双频率、天线高度可调节情况下的值小，其他情况均比双频率、高度可调节情况的反演结果差。在波导高度为d=20 m时，频率f1=10 GHz、天线高度可调节与双频率、高度可调节情况下的蒸发波导反演高度的相对误差值相等，其他情况下都比双频率、高度可调节情况下蒸发波导反演高度的相对误差值大。由此可见，除了在某种特定情况下，单雷达频率、单天线高度、所要测量的蒸发波导高度相匹配时，具有很高的蒸发波导反演精度外，其他情况下均具有较大误差。采用双雷达频率、可调节天线高度方法在一般情况下均可提高蒸发波导的反演精度。可以预测，当采用多频段雷达，更多可调节天线高度参数时，可使得反演蒸发波导参数的精度更高。