基于机器学习的电热防除冰表面温度变化趋势预测
2021-09-03冉林熊建军赵照左承林易贤
冉林,熊建军,赵照,左承林,易贤
(中国空气动力研究与发展中心 结冰与防除冰重点实验室,四川 绵阳 621000)
飞机电热防除冰是指利用电加热方式使飞机重要部件表面温度保持高于冰点温度,以防止部件表面结冰,或融化与部件接触的冰界面,进而使冰在外力下脱落,避免飞机气动外形遭到破坏的一种防护手段[1]。电热防除冰的周期性加热方式[2],具有能耗低、利用率高、加热元件损耗低[3]等优点,是机载电加热系统常采用的工作方式。处于周期通电状态的电加热系统,若温度随环境变化呈上升趋势,加热元件保持通电就会产生过剩的热量,易造成元件损坏,系统不能正常工作。如果能根据当前状态,提前得到部件的表面温度变化趋势,可有效避免此类危害的发生。因此,对电热防除冰表面温度变化趋势的预测有着重要意义。
飞机电加热防除冰主要涉及防除冰系统设计[4]、电热防除冰热载荷计算[5-6]、防除冰部件材料性能探究[7]等,都是围绕着对象的温度变化来开展,所以对电热防除冰部件表面温度的研究是非常有必要的。文献[8]运用数值计算模拟了某电热防除冰部件供电工作时的热流变化,优化了电热系统的功率分布。文献[9]研究了旋翼电热周期控制律防除冰,比较了不同部件使用不同控制律的应用效果,表明了周期控制律的有效性。文献[10]详细概述了防除冰温度控制系统设计的具体内容。文献[11]运用数值计算,以飞机设计标准和飞行工况作为约束条件,提出了多状态的电热系统供电功率的优化方法。文献[12]基于焓法模型,对周期控制律电热部件表面温度变化进行了计算,表明合理的控制律可提升系统的应用效果。上述研究工作中,温度都是通过计算的途径得到的,工程计算精度有待提高,数值计算时间代价较大,也无法对下一时刻的温度进行预测。
文中提出了基于机器学习的电热防除冰表面温度变化趋势的快速预测方法,以电加热模型的结冰风洞试验[13]为基础,引用机器学习的有监督学习方式[14-15],随机划分试验数据为训练集和验证集,通过KNN近邻回归[16]、局部加权回归[17]两种机器学习算法做温度变化率预测,进而获得温度变化量,并与前项温度求和,组成下一输入特征,以获得连续的预测温度。与实际测量的温度进行对比,验证运用机器学习方法预测飞机电加热部件进行防除冰时表面温度变化趋势的可行性。
1 试验
1.1 试验设备
中国空气动力研究与发展中心 3 m×2 m结冰风洞[18-19]是一座闭口回流式高亚音速风洞,主要包括喷雾系统、制冷系统、高度模拟系统、风机动力系统,如图1所示。该风洞拥有主试验段、次试验段和高速试验段等3种类型试验段,文中选用主试验段来开展电加热防除冰试验。
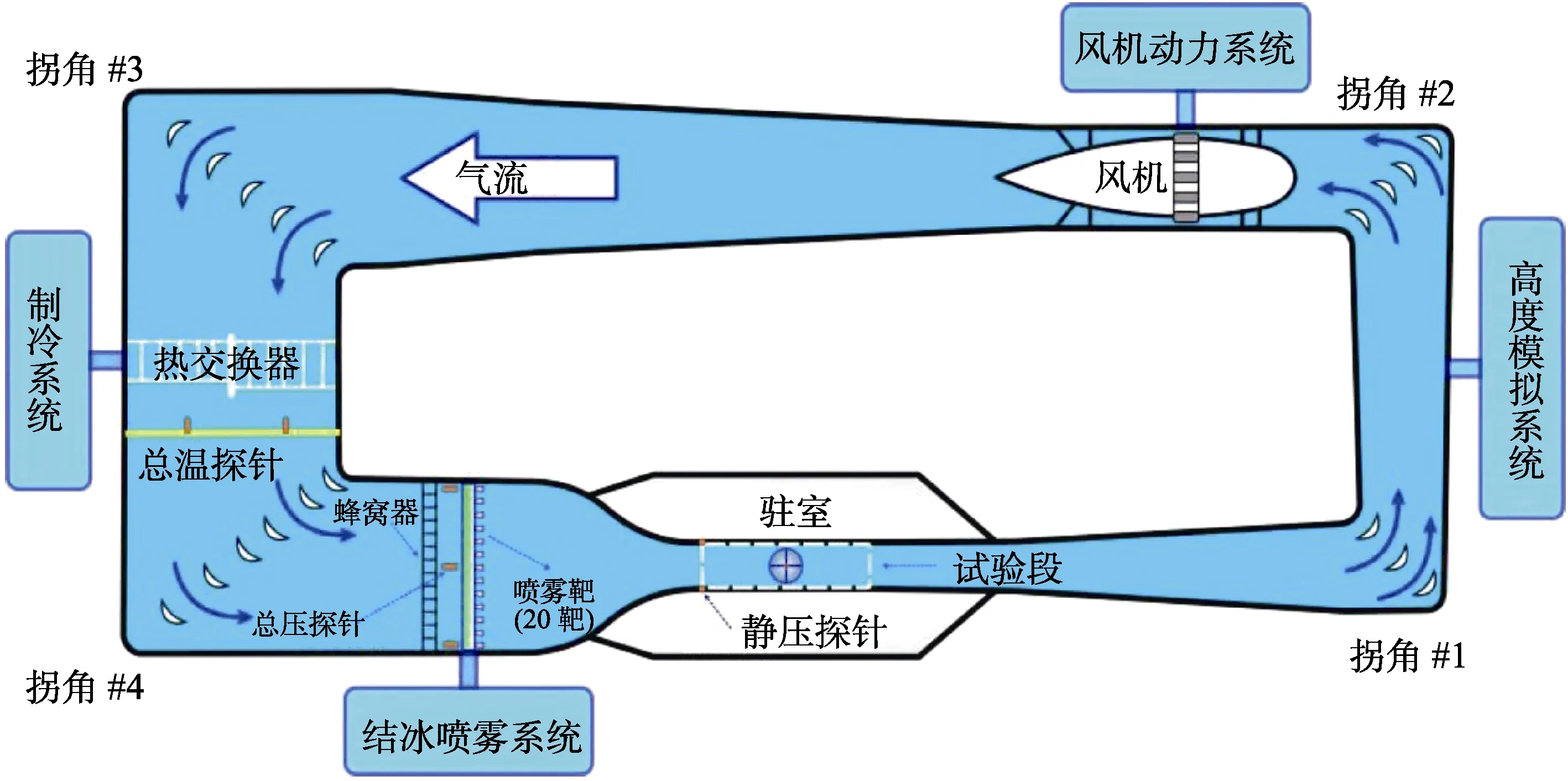
图1 3 m×2 m结冰风洞Fig.1 3 m×2 m icing wind tunnel
另外,为满足多种方式电热防除冰试验需要,3 m×2 m结冰风洞专设有独立的高性能多功能电加热防除冰控制系统[20],提供DC28 V、DC270 V、中频400 Hz/AC115 V等实际机载使用的可调电源,接入风洞测控环网,融入整个风洞设备体系,系统结构如图2所示。

图2 结冰风洞电加热防除冰控制系统结构Fig.2 Structure of electric heating anti-icing and de-icing control system for icing wind tunnel
按照电加热操作流程,设计下位机控制器和上位机界面的程序,实现运行状态监视、温度开环控制、温度闭环调压或间断控制、数据采集等功能。其中周期性电加热控制律应用系统的温度开环控制模式,由上位机配置电加热的通、断电延续时间,试验模型的防除冰区域被周期性加热,其表面温度有规律地变化。
1.2 试验模型
此次研究的电加热模型是弦长 350 mm的螺旋桨,其电加热元件沿前缘展向两侧布置,在同一截面垂直距离间距2 cm布置5个温度传感器,测量截面的温度分布,传感器的布置如图3所示。加热元件附着于模型前缘两侧,温度传感器埋于蒙皮内侧,温度测量点以P3为中心,左侧P1、P2,右侧P4、P5。
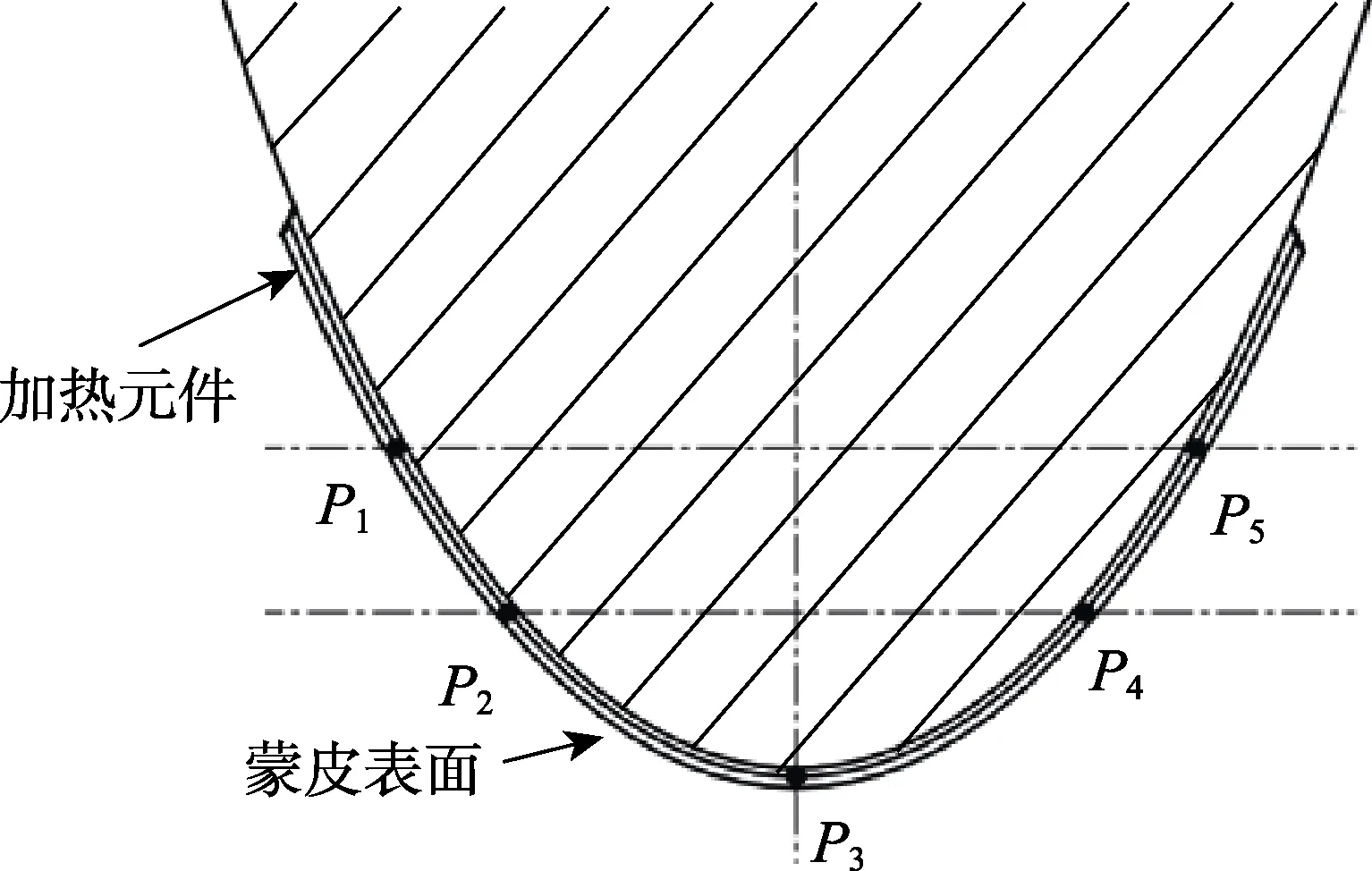
图3 截面温度传感器布置Fig.3 Schematic diagram of cross-section temperature sensor arrangement
1.3 试验条件
模型采用周期电加热方式进行试验,单个加热周期为50 s,其中通电时间为25 s、断电时间为25 s。模型电热元件上电输出的电流变化如图4所示。共开展了4组试验,试验参数主要包括风速v、来流温度θ∞、粒径dMVD、液体水含量ρLWC,见表1。
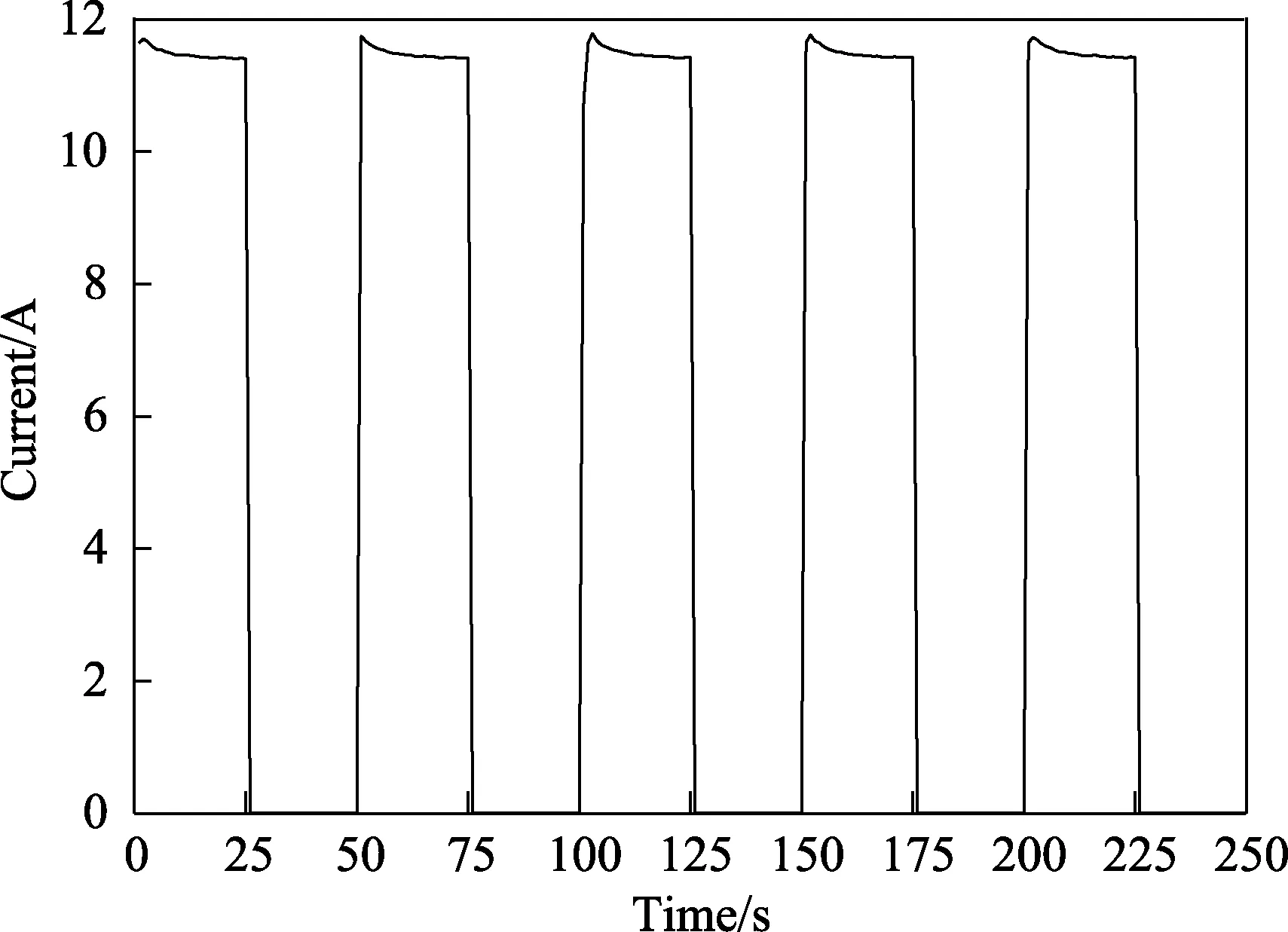
图4 电热元件通电25 s、断电25 s输出电流变化Fig.4 The output current changes of the heating element is powered on for 25 s and off for 25 s
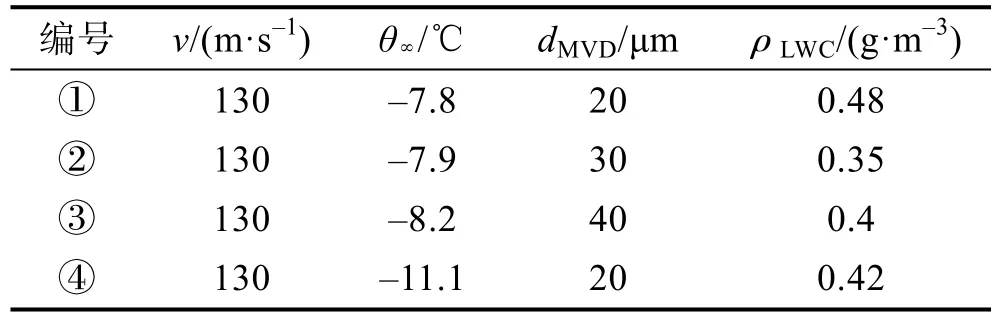
表1 周期电热防除冰试验工况Tabl.1 Periodic electric heating anti-icing and de-icing test conditions
1.4 试验结果
表1的4个条次试验,电加热系统输出如图4所示的加热周期,并采集、存储试验相关参数数据以及表面温度数据。模型测温截面5个点位温度变化如图5所示。
由图5可见,截面两侧P1、P2、P4、P5位置的温度变化与电流变化规律一致,通电温度上升,但通电结束后延续约2 s,因剩余热量,温度仍在上升,然后下降。由于前缘P3位置液态水蒸发量最大,在通电阶段出现温度上升滞后,温度变化呈现无次序上升、下降。
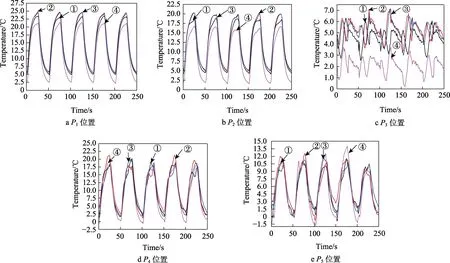
图5 模型测温截面5个点位温度变化Fig.5 Model temperature measurement cross-section temperature changes at 5 points: a) P1 position; b) P2 position; c) P3 position; d) P4 position; e) P5 position
2 表面温度机器学习模型构建
2.1 样本特征参数的构建
此次通过试验得到表面温度数据及相关试验参数数据,作为用于机器学习的训练集和验证集。飞机部件在电热防除冰过程中,电加热元件通电提供热源,所产生的热量主要通过加热区域表面的对流换热、液态水蒸发吸热、部件内部热传导以及向周围环境辐射等方式耗散,并在部件表面的温度变化上体现出来,所以表面温度ts与影响其变化的相关参数之间的关系可表示为:

从能量守恒角度出发,模型表面温度变化量主要与控制律的供电规律、模型表面温度、风洞环境温度相关。定义同一时刻供电电流为It、表面温度为θst、试验环境温度为θEt。因此,表面温度变化率则可表示为:

式(2)中:上标t指所有变量在t时刻的值。引入机器学习的有监督学习方式,将It、θst、θEt作为输入特征,温度变化率sθ˙作为输出特征,表达式为:

式(3)为根据试验所得表面温度数据下一时刻t+1与当前时刻t的差值来计算温度变化率。
按照通、断电周期,划分试验数据为若干样本,从中选出训练集和学习集,如式(4)—(6)所示:

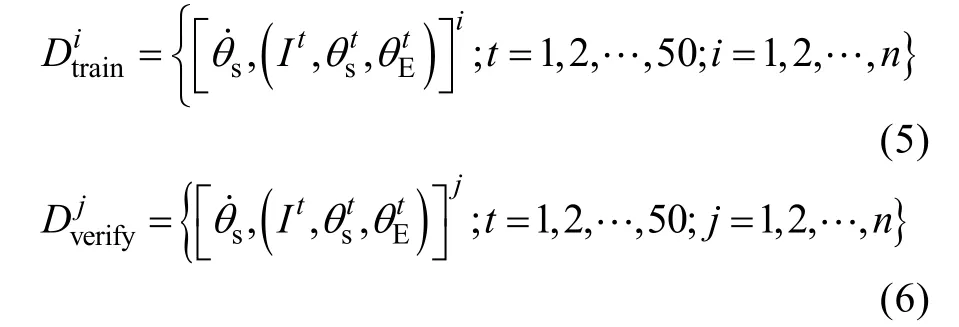
式(4)为总体样本,式(5)为训练集样本,式(6)为验证集样本。根据表面温度变化率的特征参数关系式,通过监督学习算法对训练集样本分析推算,得到输入、输出特征之间的映射函数:

2.2 表面温度的有监督学习方式
由于表面温度变化率是连续的,可将其求解转化为有监督学习中的回归问题,具体流程如图6所示。验证集通过特征参数的映射函数预测表面温度变化率,从而得到其温度变化量。然后与当前时刻t的表面温度求和得到下一时刻t+1的表面温度,再与另外的输入特征变量组合,进行下一次预测,得到验证集样本的温度变化率预测结果,并转换为温度,从而获得周期电热防除冰表面温度的变化趋势。

图6 表面温度有监督学习流程Fig.6 Supervised learning process of surface temperature variation
其中,回归算法选用局部加权线性回归算法和KNN近邻回归算法。局部加权线性回归算法是引入高斯核对样本的每个预测点,赋予一定的权重,对训练集样本做线性回归计算,得到其映射函数。所述高斯核函数W和回归系数w的表达式为:

式(8)中:xi为样本的第i个点;xc为样本的中心点;θ为超参数,用于调整局部回归加权的“局部范围”。式(9)中,X、Y分别为样本的输入、输出特征矩阵。结合式(8)和式(9)可知,可改变θ值来调节算法的回归效果。
KNN近邻回归算法原理是找出样本的k个最近邻居,并将这些邻居的特征平均值赋给该样本,常用欧氏距离作为“相近条件”,表达式为:

式(10)中:di表示样本中其他点xj与预测点xi的距离。式(11)中,Xn为预测点的第n个特征;为k个近邻点中第m个点的第n个特征。KNN近邻回归是依据式(10)搜索样本预测点的k个近邻点,式(11)则将近邻点的特征作均值处理,作为预测点的特征。
3 预测结果分析及讨论
使用Pycharm软件编写KNN近邻回归算法和局部加权回归算法程序,导入训练集样本,得到特征参数的映射函数。再对验证集样本进行预测计算,得到温度变化率。再根据前项温度值转换,获得学习样本预测的温度变化。图7给出的是控制律通电25 s、断电25 s某一学习样本的表面温度变化预测。图中方形符号线为KNN近邻回归算法预测温度变化,三角形为局部加权线性回归算法预测温度变化,圆形为实际测量温度变化。

图7 控制律通电25 s、断电25 s某一样本的表面温度变化预测Fig.7 Prediction of the change of surface temperature of a sample in the control law with power on for 25 s and power off for 25 s: a) P1 position; b) P2 position; c) P3 position; d) P4 position; e) P5 position
由模型测温截面 5个位置的预测温度变化曲线可知,两种算法对模型两侧P1、P2、P4、P5位置预测的温度值与测量值很接近,而图7c所示的P3位置温度变化,为KNN近邻回归做的预测,更符合测量的变化趋势。为进一步比较两种回归算法的预测效果,对两种算法的预测数据分别与测量数据做皮尔逊相关系数计算,反映之间的线性相关程度。测温截面5个点位温度变化的相关系数及绝对误差和见表2。

表2 测温截面 5个点位温度变化的相关系数及绝对误差和Tab.2 Correlation coefficient and absolute error sum of temperature changes at 5 points of temperature measurement cross section%
图7和表2的结果表明,对于截面两侧位置的预测效果,局部加权线性回归算法得到的预测值与测量值的线性相关程度较高,比KNN近邻回归预测效果好。对于前缘P3位置,局部加权线性回归就不适用,预测值完全偏离了对应的测量值。该位置的温度变化符合通电温升、断电温降的规律,但不符合试验测量得到的温度变化趋势。KNN近邻回归的预测结果较符合,由于KNN近邻回归是直接使用邻近点的特征来作预测,受表面物理变化过程影响较小,得到的相关系数计算结果为80.98%,相关程度属于极度相关。就截面的全部测温点位而言,KNN近邻回归算法对于整体的预测效果较好,若想获得最佳的预测效果,可针对截面位置单独地选择预测算法。同时,另需注意机器学习方法是以样本为基础,样本数据影响预测结果的精度,所以用于预测计算的样本数据,需考虑模型导热系数、温度测量手段、数据采样率等因素。
4 结论
利用结冰风洞电加热防除冰控制系统进行了周期性电加热防冰试验,并采集、存储电加热模型的试验数据。依据模型的电加热特性以及有监督学习方式,构建了表面温度变化率与供电、表面温度、环境温度的机器学习特征参数,以预测表面温度变化趋势,得到如下结论:
1)KNN近邻回归算法适用于截面的所有测温点位,而局部线性加权回归算法对前缘位置不能作出准确的预测,但对于其他位置,比KNN近邻回归的预测效果好。
2)应用两种机器学习算法做预测计算,其结果与真实测量数据的线性相关系数达到80%以上,表明机器学习的方法可用于预测电加热防除冰部件表面温度变化趋势。
