基于超像素分割的孪生网络双目立体匹配方法研究

陆 玮，刘 翔，薛 冕

(上海工程技术大学 电子电气工程学院,上海 201600)

立体匹配的目的是通过匹配双目图像中的对应像素点，得到左右相机图片的视差图。这不仅是双目立体视觉技术的关键，也是目前三维重建领域的研究重点[1]。为了提高匹配精度，需要克服图像中存在的弱纹理区域、遮挡区域以及边缘深度不连续等诸多问题[2]。主流立体匹配算法框架分为以下4个步骤[3]：

(1)匹配代价计算。代价计算目的是获得左右图像间视差的灰度相似性，通常情况下，匹配代价越低则越相似；

(2)代价聚合。匹配代价聚合是使用聚合窗口与视差平面卷积。由初始匹配代价来构造能量函数，然后通过局部算法对窗口进行叠加处理，将能量函数优化为全局最小值，从而提高匹配代价聚合计算的可靠性；

(3)视差计算。目前主流的视差计算分为基于全局和半全局两个方向[4]。基于全局的算法使用包含数据项与平滑项全局能量函数。数据项是像素的匹配代价值，平滑项则对视差值的波动进行了抑制，使之平滑，然后通过最小化全局能量函数，得到最优的视差图。而半全局的算法(Semi-Global Matching，SGM)使用基于像素、互信息(Mutual Information，MI)作为匹配代价，然后通过能量函数进行代价聚合，并采用动态规划来最小化能量函数以寻找最佳视差[5]，局部立体匹配实时性较好，应用较为广泛；

(4)视差优化。初始视差被提取之后精度比较低。对于一些精度要求较高的需求，可以在初始视差的基础上，采用亚像素增强等方法进行细化求精。同时也可以通过中值滤波、左右一致交叉检测算法等后处理过程，去除遮挡区域以及误匹配点，修正和滤除计算后的视差值，从而获得较高的精确度。

随着深度学习方法向计算机视觉研究领域的引入，从2016年文献[6]首次将卷积神经网络(Convolutional Neural Network，CNN)技术应用到立体匹配算法之后，基于深度学习的方法逐渐展现出优势。下面将分别对半全局匹配算法、AD-Census算法以及本文提出的基于超像素分割的孪生网络方法进行介绍和对比。

1 半全局匹配算法

半全局匹配算法是一种基于动态规划方法改进的立体匹配算法[7]。该方法使用 8个方向均匀的一维路径对图像做动态规划计算，然后再将各个方向的计算结果进行合并。立体匹配问题可以变成寻找最小能量问题，能量函数为

(1)

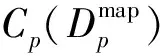
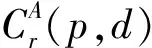
(2)

其中，r是单位方向向量。

半全局匹配算法虽然能够获得较为准确的视差图，但在噪声环境和视差图纹理边缘的准确度仍存在局限性。

2 AD-Census算法

Census变换是一种非参数化变换，用来表征图像的局部结构特征[8]。其以一个矩形窗口遍历图像，然后比较窗口中邻域像素与中心像素灰度值的大小。若灰度值小于中心像素的记为1；大于等于中心像素的记为0。将这些值按位连接成一个矢量作为中心像素的特征值，用汉明距离来表示相似度测量。

2.1 AD-Census联合匹配代价

计算式如下

(3)

其中，Ccensus(p,d)是Census变换的匹配代价；CAD(p,d)是SAD(Sum of Absolute Differences)的匹配代价；λcensus与λAD是调节Census与SAD之间比重的参数。函数ρ(c,λ)用于控制每个变换结果的取值范围为[0,1]。

2.2 Cross-based代价聚合

图1 半全局匹配算法基本流程Figure 1. SGM algorithm flow

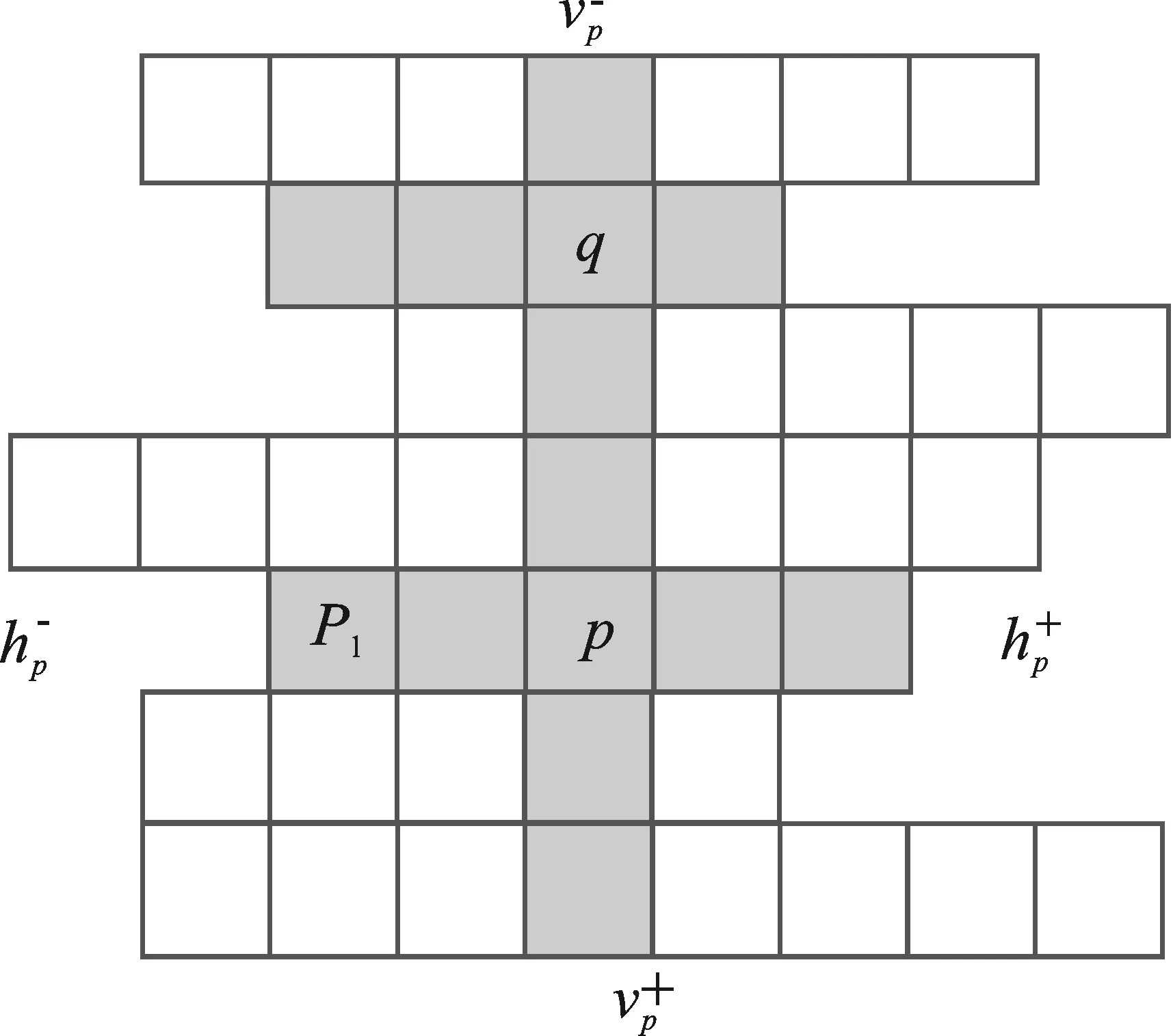
图2 动态十字交叉域Figure 2. Dynamic cross field

聚合代价计算式为式(4)。

(4)

相比于单独使用基于SAD或Census变换的代价计算，基于AD-Census的代价计算可以产生更精确的匹配结果。Census变换在重复或相似的区域结构会产生错误匹配，而SAD对于大面积缺乏纹理特征的区域很难完成有效的匹配。结合两者优点的AD-Census匹配算法可以减少其单独使用所产生的错误匹配。改进之后的视差图对比如图3所示。

(a) (b)图3 视差对比(a) SGM方法 (b) AD-Census方法Figure 3. Disparity comparation (a)SGM method (b)AD-Census method

3 Siamese孪生网络

本文使用结合超像素边缘信息的Siamese孪生网络视差预测方法[10]。该方法网络左右两个通道同时接收两张图片的输入，通过多级的卷积、激活函数结构进行特征的提取、变换、融合，最后得到一个低分辨率、高通道数的图像特征，完成全局信息融合与理解。然后，利用提取特征的描述算子来计算两个图片特征向量，通过Loss函数计算，从而判断相似度。相似度计算函数由两个特征向量构成的距离度量函数决定，计算式为式(5)。

(5)

最后匹配得到代价体积(Cost Volume)并获得视差图。整个算法流程如图4所示。

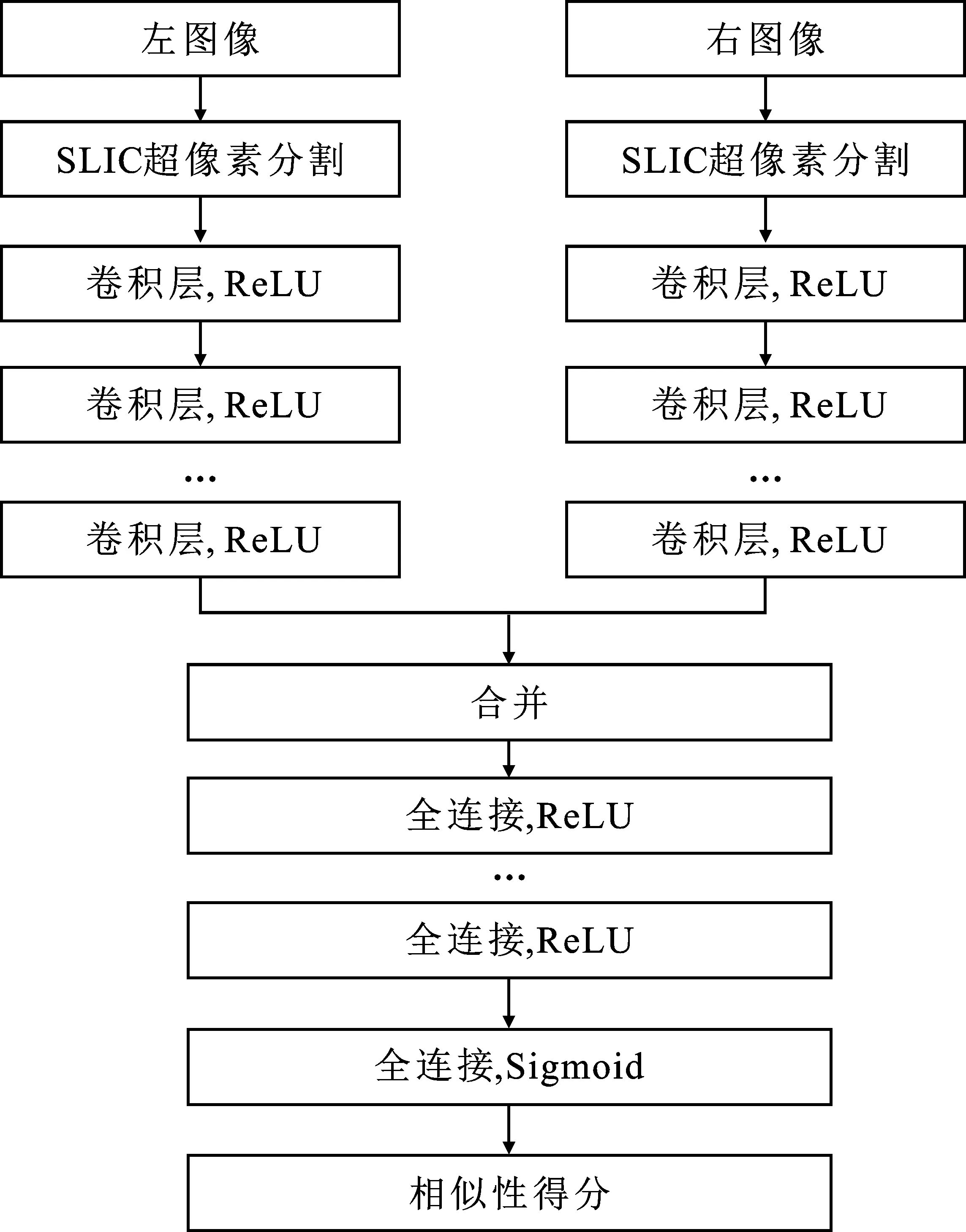
图4 超像素分割的孪生网络立体匹配算法流程Figure 4. Super-pixel segmentation of the Siamese network stereo matching algorithm flow

3.1 训练集构建

本文使用Middlebury中的双目图像数据集作为训练集。完整的图像数据无法直接作为网络的输入，需裁剪为图5的正负样本像素块。

图5 训练样本 (a)正样本像素块 (b)负样本像素块Figure 5. Training sample (a) Positive sample pixel block (b) Negative sample pixel block

3.2 样本标准化

图像样本在裁剪后的范围为[0,255]，通过标准化将式(6)～式(8)处理到[-1,1]范围内。

(6)

(7)

(8)

式中，xi是原始图像X中各像素灰度值；S是标准差；X是经剪裁后的灰度矩阵；U是标准化后的灰度值矩阵。

4 基于超像素分割代价聚合改进

针对局部立体匹配算法在光照不均匀、纹理缺乏等复杂环境下，容易造成物体边缘的视差图存在大量误匹配点的问题，本文提出基于SLIC(Simple Linear Iterative Clustering)超像素分割[11]的立体匹配改进算法。该方法采用均值滤波预处理基准图像，并使用SLIC算法进行超像素分割，把图像分割成像素块作为Siamese孪生卷积网络的代价聚合的输入。在代价聚合步骤中，根据基准图像的超像素分割结果，动态地调整能量函数的平滑系数。

4.1 SLIC算法

边缘特征是计算机视觉等领域中经常使用的重要信息。相较于点特征，边缘特征具有以下优点：(1)直线在遮挡的情况下不会受到很大影响；(2)在纹理匮乏的区域，特征点难以检测，而边缘线则相对比较容易；(3)直线之间存在几何关系，可以作为约束条件来提高处理精度。

对于立体匹配得到的深度信息，利用颜色相似区域有相同的视差这一原理，可认为超像素体中的像素块有相同的视差。SLIC简单线性迭代聚类方法相对于其他超像素分割算法，具备较高的运算效率和可并行的特性，计算复杂度低，可应用于实时的立体匹配[12]。

SLIC算法流程如下：

(1)把图像从RGB色彩空间转换到CIE-Lab色彩空间，每个像素的(L,a,b)颜色值和(x,y)位置坐标组成5维向量V[L,a,b,x,y]。两个像素的相似性可以通过向量距离来判断，距离越大，相似性越小；

(2)聚类初始化中参数值k表示大小相等的超像素个数。在间隔S像素的规则网格上采样，其中网格间隔为

(9)

(3)为了避免将超像素定位在边缘上，同时尽可能地减少使用噪声像素，将中心移动到与3×3邻域中最低梯度位置相对应的种子位置；

(4)将聚类中心调整为窗口内像素的平均向量V[L,a,b,x,y]，然后在2S×2S的预期空间范围内，进行类似像素的搜索。相对于K-means聚类，该方法缩小了搜索范围，降低了距离计算复杂度，两个方法的像素搜索对比如图7所示。

SLIC相较于其他算法的优点包括：(1)将具有相似亮度、颜色、纹理等特征的像素聚集成像素块，得到良好的物体边缘轮廓；(2)可以分割彩色图和灰度图；(3)参数量非常少，只需要设置一个预分割的聚类中心数量k；(4)加权距离度量组合颜色和空间接近度，生成超像素图像的尺寸、紧凑性和轮廓都比较理想。SLIC超像素分割图像结果如图8所示。

4.2 基于超像素分割的代价聚合方法改进

基于同一超像素内物体表面的相邻像素视差值变化较小，而不同超像素之间的空间连续性较差的特点[13]。本文对基准图像使用 SLIC 算法进行超像素分割，获得具有良好纹理边缘的分割图像。然后根据超像素分割结果，对代价值聚合方法进行改进，动态调整原来立体匹配能量函数的平滑系数。具体方法如下：

(1)对于同一超像素内，或者属于不同超像素但相邻像素色彩差值小于设定阈值的情况，令能量函数中的平滑系数P2保持不变；

(2)对属于不同超像素并且相邻像素色彩差值大于设定阈值的情况，把能量函数中的平滑系数P2减小为P1。改进之后的能量函数表达式如下

(10)

(11)

(12)

式中，Ip、Iq分别是相邻像素p、q的RGB颜色值；segp、segq分别是相邻像素p、q所在的区域；It为色彩差值阈值。

通过 SLIC 超像素分割方法的改进，可以有效减少图像纹理边缘处的视差误匹配问题。

5 实验结果

为了验证本文算法的有效性和可行性，对该算法和原半全局匹配算法进行实验与比较[14-15]。

实验数据采用的是学术界公认的Middlebury立体视觉数据库。该平台提供多种场景双目图像，同时提供了双目图像的真实视差图和标定参数[16]。现将本文改进后的算法与SGM算法、AD-Census算法分别提交到Middlebury平台中，用Teddy、Cones、Tsukuba共3组图像的标准视差图进行对比分析。

图9～图11是利用本文算法和传统方法对3组测试图像进行立体匹配的直观结果对比。其中，图9(a)～图9(d)分别为原始图像、本文改进算法视差图、SGM算法视差图以及AD-Census算法视差图。

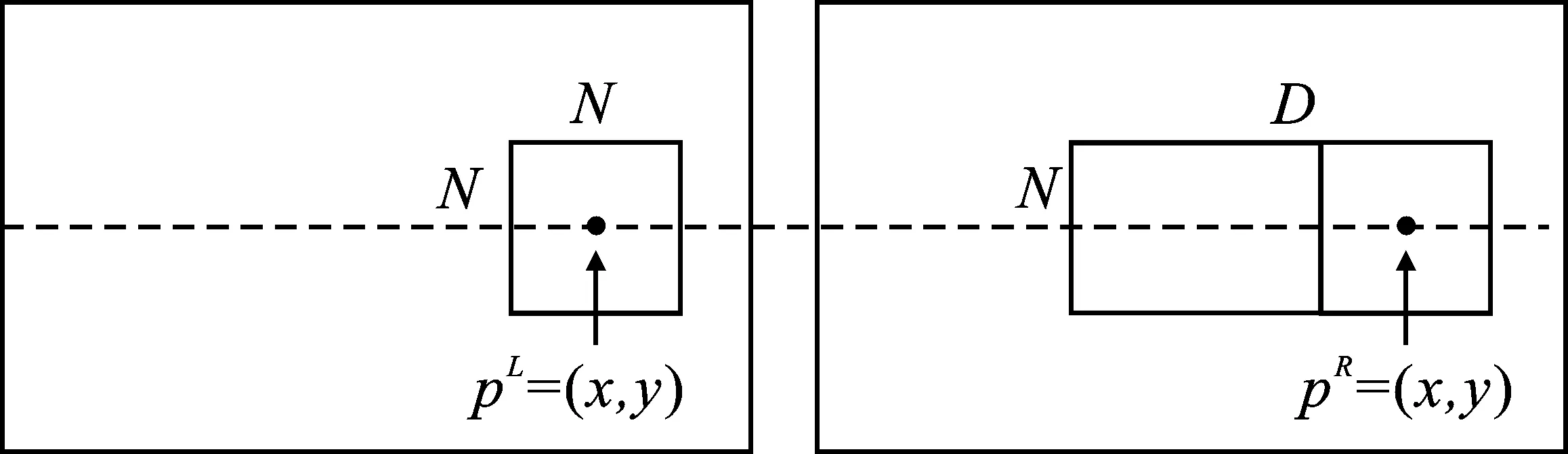
(a) (b)图6 样本裁剪示意图 (a)左图 (b)右图Figure 6. Sample clipping diagram (a) Left diagram (b) Right diagram

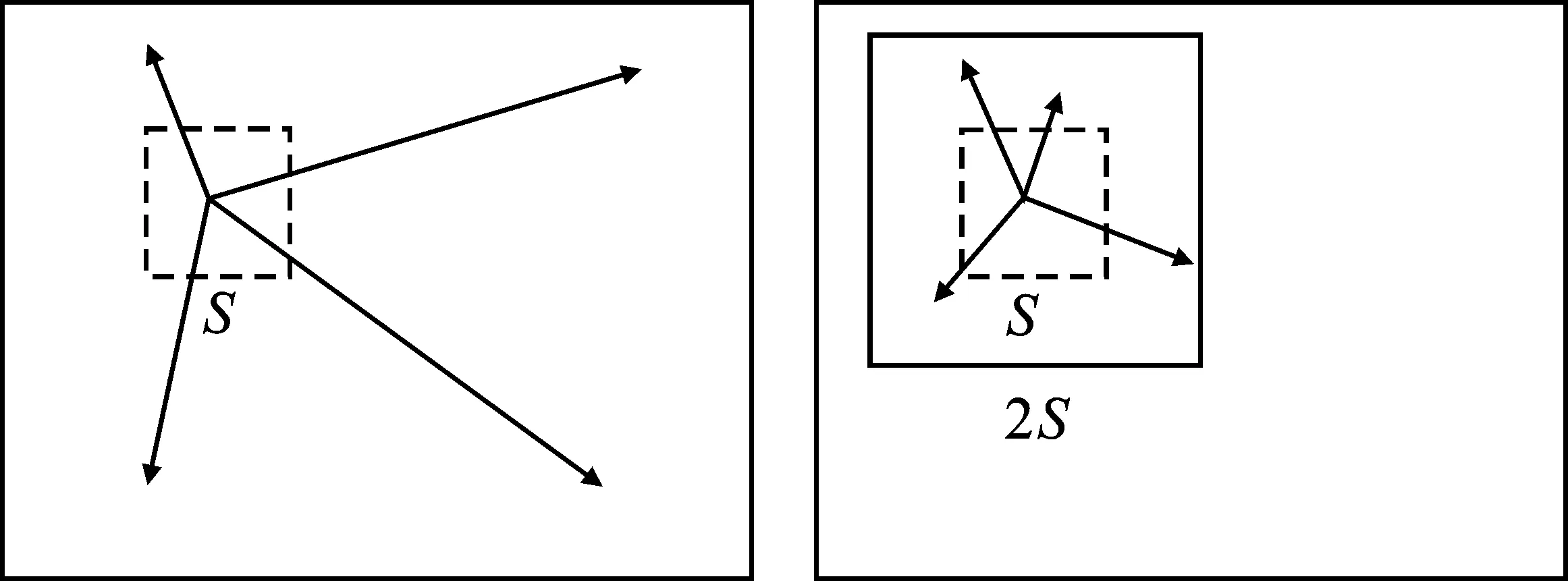
(a) (b)图7 像素搜索区域对比 (a)K均值算法 (b)SLIC算法Figure 7. Pixel search area comparison(a) K-means algorithm (b) SLIC algorithm

(a) (b)图8 SLIC超像素分割 (a)原图 (b)SLIC分割结果Figure 8. SLIC super-pixel segmentation(a) Original image (b) SLIC segment result

(a) (b) (c) (d)图9 Teddy样本视差图对比(a)原图 (b)本文算法 (c)SGM (d)AD-CensusFigure 9. Teddy disparity map comparison (a)Original image (b)Proposed algorithm (c)SGM (d)AD-Census

(a) (b) (c) (d)图10 Cones样本视差图对比(a)原图 (b)本文算法 (c)SGM (d)AD-CensusFigure 10. Cones disparity map comparison (a)Original image (b)Proposed algorithm (c)SGM (d)AD-Census

(a) (b) (c) (d)图11 Tsukuba样本视差图对比(a)原图 (b)本文算法 (c)SGM (d)AD-CensusFigure 11. Tsukuba disparity map comparison (a)Original image (b)Proposed algorithm(c)SGM (d)AD-Census

从实验对比结果可以看出，本文改进的基于超像素分割的孪生网络立体匹配方法与传统的SGM算法、AD-Census算法相比，在Nocc和Disc区域[17]的平均误匹配率明显较低，对不同的场景均能生成较好的视差图。在Tsukuba测试图像中，本文算法视差图的边缘更加平滑。而在Cones、Teddy测试图像中，本文算法获得的视差图边缘区域和遮挡区域的匹配精度都得到了较好提升，相比传统方法取得了更好的改进效果。

本文所提算法的平均视差误差和平均错误率[18-19]都有所降低，结果如表1所示。

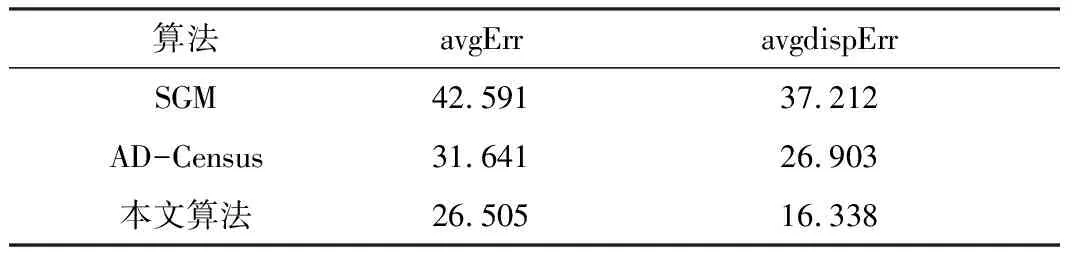
表1 匹配代价算法对比

6 结束语

本文对双目立体匹配算法进行了深入的研究和分析，对主流方法进行了对比和论述。针对纹理缺乏、边缘深度不连续等情况容易导致双目匹配精度低的问题，提出了基于超像素分割的Siamese孪生网络匹配算法。该方法对前端的输入图像进行预处理分割，确保同一个分割区域内是连续的像素块，然后分别对分割之后正负样本的像素块进行训练。

实验结果表明，本文算法对Middlebury公开数据集的平均视差误差和平均错误率都有降低，相较于其他算法具有更好的鲁棒性，并且在深度不连续区域得到了有效的匹配，匹配准确率有一定地提升。但在前景颜色与背景颜色较为接近的区域，由于容易引起错误分割，导致在此类情况下的匹配效果并不理想，这也是下一步研究中需要改进的地方。