浅谈支持向量机在心脏病预警中的应用

赖俊豪

华南农业大学/电子工程学院（人工智能学院） 广州 广东 510642

引言

当今社会下，高糖高脂的饮食、高涨的生活压力、不良的生活习惯如吸烟、久坐不动等，已然成为心脑血管疾病的主要诱导因素。据美国心脏病学会研究表明，过去5年间，罹患各类心脑血管疾病的人数上涨了49.2%，因此造成的直接或间接经济负担更是高达3634亿美元每年[1]。在2019年间，中国总死亡人数中有71%死于非传染性疾病，而心脑血管疾病是非传染性疾病中排行榜首的致死因素，占比达到了惊人的44%[2]。心脏作为人体的重要组成部分，其任意微小病变都有概率致残甚至致死，严重威胁人类身心健康。尽早发现心血管病便能尽早治疗，便可能及时挽救人类的生命，减少不必要的社会支出，这说明对心脑血管疾病的提前预警具有重大意义。

心血管病起因复杂，早期症状不明显，传统的医疗诊断模型对这类疾病预测效果不佳，导致患者错过黄金治疗期。而机器学习可以自主地挖掘数据间的内在联系，建立预测模型，预测患者患病风险。目前国内诸多学者曾开展过研究，其中大部分研究都是基于UCI心脏病数据集，如叶苏婷等人采用决策树算法进行研究，取得了81%的准确率[3]；刘宇等人采用K邻近算法与XGboost算法相配合，取得了85%的准确率[4]；王健等人通过神经网络算法建立模型，取得了89%的准确率[5]。在建立模型时，不同的机器学习算法的预测准确率不同，即使是相同的训练集相同的算法，选择不同特征变量的，也会导致结果的不同。本文选取UCI提供的心脏病数据集作为研究对象，并利用梯度提升树与支持向量机算法相配合来构建模型，并与部分其他算法进行比较，寻找其中预测效果最优的算法。

1 算法介绍

1.1 GBDT算法

梯度提升树是以决策树为基础的算法，对真实分布具有出色的拟合度，其原理是每轮迭代在上一轮模型的残差基础产生

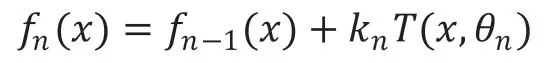
一个新的决策树，并将所有的决策树相加即是搭建的模型，经过n轮迭代后，模型可以表示为：是已经构造的n-1棵决策树所组成的模型，而是我们当前需要构造的第n棵决策树，代表决策树的系数，即是残差，可以用下式近似表示：

其中：N代表样本的总个数，L代表损失函数。在本文中使用的损失函数是对数损失函数：

在每轮迭代时，通过使损失函数快速减小，从而使模型可以快速收敛。

1.2 特征筛选

GBDT不仅可以原来建立模型，还可以用来筛选特征，这也是GBDT算法在本文中的应用。通过遍历每种可能的决策树组合，某一特征的重要性可以根据其对输出结果的影响来衡量，但这会涉及大量复杂的计算，而Friedman提出了一种简便的方法，即是通过特征在所有树中的平均重要度来衡量其对整体的贡献性[6]，其表达式如下：

其中：M是树的数量，L是第M棵树的叶子节点数量，L-1是该树的非叶子节点数量，而是节点分裂之后损失函数的减少值。特征的重要度越高，那么在特征节点在分裂时损失函数减少得便越多，根据不同特征中重要度的排序，就可以知道不同特征的优先级。

1.3 SVM算法

支持向量机分类器是最大间隔分类器的推广，其算法的核心思想是根据数据样本的空间分布特点，寻求一个合适的超平面将样本空间分割，以此达到分类的目的。

为方便理解，可以将遐想在一张白纸上散落着红豆与绿豆，若在白纸上描绘坐标轴，用X轴表示颜色，Y轴表示大小，那么红豆与绿豆便会分成泾渭分明的两堆，其间可以用一条直线表达式表示分界线，这便是最大间隔分类器的作用。但如果将红豆与绿豆替换为红豆与赤小豆，采用相同的坐标系便无法有效区分。考虑将大小这一维度扩展为Y轴表示长度，Z轴表示宽度，那么将可以找到一个平面将两者区分开来，这便是支持向量机的作用。将其推广到N维空间中，那么分割面便是一个N-1维的平面仿射子空间，可以用如下线性方程来描述：

到该平面的距离可以表示为：

的值即是间隔，通过上式计算符合样本数据的最大值，其所对应的曲面即是最大间隔超平面。可以看到，寻找目标曲面的重点是最大化间隔即是要最小化即是要求解以下优化问题：

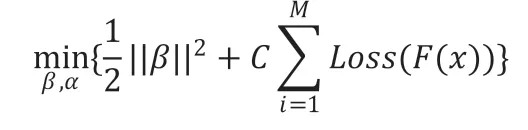
通过求解优化问题，可以得到相关的模型参数 和，从而创立支持向量机模型。而分类可以通过定义如下函数来判断：

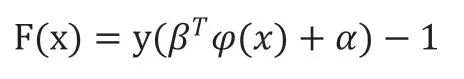
2 实验流程

2.1 数据集介绍

近年来UCI心脏病数据集比较热门，被广泛应用在各种研究中，其原始数据包含了303个样本，75个特征与1个标签。遍历数据集，人为的去除序号、姓名和社保账号等与训练无关的特征，去除含有未知项和重复项的特征，此时剩余59个特征。利用GBDT算法进行特征筛选，采用重要性前10的特征进行模型搭建，部分特征的重要度如图1所示。

图1 部分特征重要性

精简后的数据集包含10个特征与1个标签，如下表1所示。

表1 特征介绍

2.2 数据归一化

数据集中无缺失值，但可以注意到不同特征值的表达情况不同，有的用连续值表示，有的用离散值表示，各特征的量纲也有所差异。为了清除不同特征间差异的影响，需要进行归一化。随后，从样本中随机抽取作为测试集，其余部分作为训练集，即训练集有243个样本，测试集有60个样本。

2.3 模型分析与对比

采用训练集用来搭建基于支持向量机算法的预测模型，并用测试集测试模型的可靠性，随后采用逻辑回归模型算法与随机森林算法进行模型搭建，对三者进行比较。其中支持向量机模型选择参数为核函数为linear函数，惩罚系数为1，逻辑回归模型采用默认阈值，即为0.5，随机森林模型选择参数为最大决策树数目为20，随机状态数为12，决策树最大深度为7。通过网格搜索法对支持向量机模型与随机森林模型参数进行优化，优化后支持向量机模型使用RBF函数(gamma值为0.1)作为核函数，惩罚系数为2，随机森林模型最佳参数为最大决策树数目为40，随机状态数为12，决策树最大深度为6。而逻辑回归模型则通过改变阈值探究影响，发现在阈值为默认值时模型已经达到最优。不同模型的准确率、精确率、召回率与F1值如表2所示。

从表2中可以看出，支持向量机模型不论在优化前后，皆表现出了比逻辑回归模型与随机森林模型更好的拟合性。因为在UCI的心脏病样本中，患病人数与非患病人数相差无几，所以可以看到各模型的准确率与精确率高度相似，但在实际中，患有心脏病的是少部分人数，召回率是一个更有参考意义的值，它表征了我们所能正确预测心脏病患者的比例。而F1则可以表示分类器的优劣性，值越高则说明分类效果越好。在本实验采用的三种算法中，支持向量机算法对UCI心脏病的数据集建模效果较好。

表2 不同模型评价对比

3 结束语

本文通过使用支持向量机算法，建立了心脏病预测模型，并与逻辑回归算法与随机森林算法搭建的模型进行了比较，结果表明支持向量机算法效果更优秀，可以有效预测心脏病发病风险。在本文实验流程中，支持向量机模型准确率为0.92，精确率为0.92，召回率为0.91，提示其在目标数据样本上具有优良的分类效果。但本模型仍存在改善空间，如采取更多的效果数据集进行验证，或采取不同的优化算法进模型进行优化。