水力发电机组甩负荷过渡过程的参数敏感性分析

2021-09-02谢卓健闫懂林麦先春王峻峰陈启卷

中国农村水利水电 2021年8期

谢卓健，闫懂林，肖汉，麦先春，王峻峰，陈启卷

（1.四川大唐国际甘孜水电开发有限公司，四川康定626001；2.武汉大学动力与机械学院，武汉430072）

0 引言

在过去的二十年里，我国水电的开发和利用得到了快速的发展，在西南地区，各种大流量、高水头、包含复杂水力系统的水电站不断兴起。到2019年底，我国的水电总装机容量已经达到3.56 亿kW［1］。对于水电站来说，由于电网故障等原因，运行中随时可能会经历机组甩负荷过程，而一些水电站的重大事故，例如飞逸、压力钢管爆裂等，往往就是由于这种较为极端的工况引起［2］。如何有效地保证甩负荷过渡过程中机组的安全可靠，是实际水电工程中所面临的重要问题。

到目前为止，针对水电机组甩负荷过渡过程进行了大量研究。部分学者对实际电站发生的甩负荷事故进行了分析和讨论。黄菊珠［3］分析了山美水电站因110 kV 线路开关跳闸，造成3台机组满负荷高频切机，引发机组过速停机的事故，并提出了相关的预防措施。曲东［4］分析了平班水电站在甩负荷试验时调速器调节失灵，导叶不能回关导致机组过速停机的事故，提出了相应的处理方法，并对调速器重要参数进行了优化整定。张伟［5］针对西溪电站甩负荷试验时出现的机组过速停机及导叶快关时间不稳定等问题进行了分析，并提出了故障处理方法。除此之外，也有大量学者对水力发电机组甩负荷过渡过程进行了数值模拟研究。付亮［6］针对有调压井长引水隧洞水电站，利用数值模拟的方法研究了调压井水位波动与流道压力的变化过程。王威［7］等以伊朗卡仑水电站为例，分析了具有上游调压室、一管两机布置的水电站机组甩负荷过渡过程，并讨论了导叶关闭规律对转速上升和水击压力的影响，提出了合理的导叶关闭规律。叶文波等［8］针对南方某大型水电站，进行了机组甩负荷大波动过渡过程的计算，分析了引水系统最高压力升高和机组转速的最大升高特性。陈胜等［9］研究了水电站中机组相继甩负荷情况下调压室涌浪的叠加特性。张洋［10］研究了设置气垫式调压室的超长引水隧洞水电站的甩负荷过渡过程，提出了气垫式调压室对系统水击压力的影响效应。在这些分析和讨论中，都是在确定性框架下研究水电站机组的甩负荷过渡过程，而并没有考虑到参数不确定性对甩负荷过渡过程的影响。实际上，水电站过渡过程分析往往参数众多且包含复杂的非线性动态过程，参数尺度多样化及制造误差等多种不确定性因素均会导致计算结果的不确定性。所以，在不确定框架下研究参数对甩负荷过渡过程的影响效应就显得更有必要。

参数敏感性分析是量化系统参数在设计或设定的可能范围内变化时对系统输出响应影响的一种方法［11］。通过敏感性分析，可以获得对系统输出影响较为显著的输入参数，无论在设计、运行还是维护过程中，只需要重点关注这些参数而忽略一些不敏感的参数，就可以大大简化工作量。通常的参数敏感性分析包括局部敏感性分析和全局敏感性分析，局部敏感性分析只能反映单一参数变化对系统响应的影响，而全局敏感性分析则可以有效地反映多个参数同时变化对系统响应的影响［12］。在全局敏感性分析方法中，主要包括：回归分析法［13］、筛选法［14］，Sobol 指数法［15］和扩展傅里叶幅度检验法（extended Fouri⁃er amplitude sensitivity test，EFAST）［16］等。其中EFAST 方法可以获得输入参数之间的交互效应，已经在很多领域得到了广泛应用［17，18］。因此，本研究中将利用EFAST 全局敏感性分析方法来研究水力发电机组在甩负荷过渡过程中输入参数对转速、水击压力和调压室涌浪的敏感性特性。

相比于之前的研究，本文的主要创新在于考虑参数的不确定性，在不确定框架下建立了水力发电机组的甩负荷过渡过程的模型，并以此模型为基础进行了数值研究，量化分析了输入参数对机组甩负荷过程中机组转速、水击压力和调压室涌浪的敏感性特性。相关的理论方法和研究结论可以应用于水电站的设计及维护工作。

1 水力发电机组甩负荷过渡过程建模

水电站的引水系统在空间分布上主要包括上游水库，引水隧洞，上游引水调压室，压力钢管，蜗壳，尾水管及尾水明渠段。本节将首先利用特征线方法建立该电站引水系统的数学模型，同时结合水轮机特性曲线的插值模型，调速器数学模型，发电机及负载数学模型，建立完整的水电机组甩负荷过渡过程的数学模型。

1.1 引水系统模型

1.1.1 有压过流管道特征线方程

利用特征线法将有压输水系统非恒定流的运动方程和连续性方程转化为在特征线dx/dt=V±a上的常微分方程组［19］，可以得到：

式中：H表示测压管水头；a表示水击波速；f为达西-维斯巴哈摩擦系数；D表示管道直径；A为流道截面面积；Q为流道中的流量。在这里，V和H是与时间和空间相关的函数，其中t为时间，x表示管道长度。

在利用特征线法离散化求解微分方程时，需要对有压管道按照等距离进行划分，得到长度为Δx的N段管，并用序号i进行标记，定义起始端为i=1，则末端为i=N+1。设定仿真步长为ΔT=Δx/a。利用特征线法进行计算机数值求解的原理如图1所示，横坐标表示管道的空间分布，纵坐标表示采样时刻分布。从中可以看出，根据上一时刻的节点i-1 和节点i+1 的值，可以计算出下一时刻节点i的水头、流量值。

图1 特征线法原理示意Fig.1 Schematic diagram of characteristics method

对公式（1）和（2）的特征线方程积分并离散化，可以得到t+ΔT时刻节点i处的水头、流量关系方程式为：

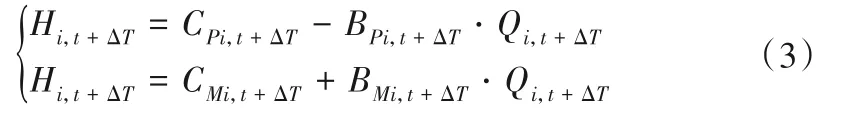
式中：B=a/Ag；R=fΔx/（2gDA2）；CPi，t+ΔT=Hi-1，t+BQi-1，t；BPi，t+ΔT=B+R|Qi-1，t|；CMi，t+ΔT=Hi+1，t-BQi+1，t；BMi，t+ΔT=B+R|Qi+1，t|。

1.1.2 水轮机边界

水轮机的瞬态工作水头定义为水轮机蜗壳进口和尾水管出口的水头差，如图2所示，当水轮机上、下游节点为1 和2 时，则水轮机工作水头为HT=H1-H2，瞬态的过机流量为QT=Q1=Q2。

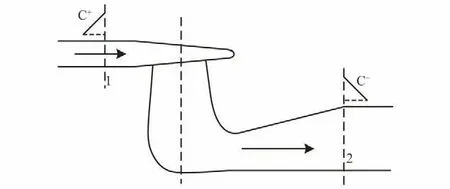
图2 水轮机简化结构图Fig.2 Structure chart of hydro-turbine

根据水轮机上下游进出口节点的水头平衡方程，可以得到：

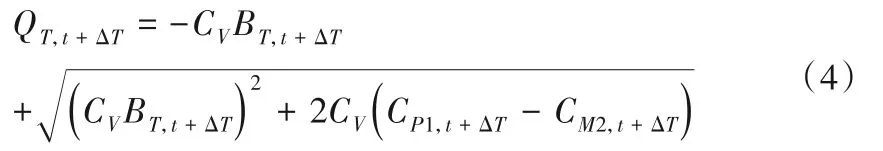
水库边界，上游调压室边界，蜗壳及尾水管当量管的计算可以参考文献［19］。

1.2 水轮机特性曲线插值模型

依据文献［20］的方法，对原始的水轮机综合特性曲线进行扩展，可以得到Q11=f1（n11，y）和M11=f2（n11，y）的关系，用于甩负荷过渡过程的计算。在这两个关系式中，n11表示单位转速，M11表示单位力矩，y表示导叶开度。以当前研究的水电站为例，得到扩展后的Q11-n11-y和M11-n11-y关系曲线如图3所示。

图3 单位流量和单位力矩图Fig.3 Diagrams of unit discharge and unit moment

1.3 发电机及负载数学模型

水力发电机组的力矩平衡方程［19］可以表示为：

式中：J为机组转动部分的转动惯量，J=GD2/4，t·m2；GD2为飞轮力矩，t·m2；ω表示机组旋转角速度，rad/s；M和Mg分别是水轮机的主动力矩和阻力矩，kN·m。

假定水轮机力矩在ΔT时刻里线性变化，则可以利用梯形积分公式对上式积分。同时，将旋转角速度（ω）转换为转速（n），可以得到：

至此，水力发电机组甩负荷过渡过程的确定性模型被建立，在这个确定性模型中将确定性的参数用不确定的分布或者范围进行替代，即可以获得不确定性的模型，以此为基础，相关的参数敏感性可以利用方便的非侵入式EFAST方法进行讨论。

2 全局敏感性分析

2.1 全局敏感性分析方法

本文采用EFAST 方法来对水电机组甩负荷过渡过程的参数敏感性进行分析。EFAST 法的原理是在输入参数的多维空间中挑选合适的搜索曲线，并给所有输入参数分配非线性相关的整数频率值，从而引入搜索函数，使模型作为独立参数的周期函数，则可以把多维积分问题转换为一维积分问题。然后通过把目标函数变为傅里叶级数，计算出各频率的傅里叶频谱曲线，由频谱曲线获得由输入参数xi引起的系统输入方差和总方差，其比值则被定义为该参数的敏感度指标。文献［16-18］中给出了具体的算法推演流程，这里仅给出敏感度计算的公式。

总方差可以写成各个子方差和的形式：

式中：V为模型总方差；Vi表示单一输入变化引起的模型方差；Vij表示通过xi和xj交互作用引起的方差；Vij…k表示xi，xj，…，xk交互作用引起的耦合方差。

主敏感性（一阶敏感性）指标表示单个参数独立作用时对系统输出响应的贡献，可以表示为：

总敏感性指标为：

式中：V-i表示不包括参数xi的所有参数方差和。

2.2 仿真设计与参数选择

以国内某水电站为例，进行机组甩100%负荷时过渡过程计算的参数敏感性分析，涉及的主要参数如表1所示。敏感性分析的输入参数均值选取设计值，方差分别取变异系数（=标准差/均值）为0.01和0.05两种情况式的值，代表不同的不确定度。选择Monte Carlo 方法进行参数的随机采样，采样样本为5 000，满足EFAST 法对样本个数的要求。另外，由于其他水工建筑物的影响，该电站不同高程下的调压室面积会有所有差别，在高程Hs0<1 458.7 m 时，面积As2为801.975 m2；当1 458.7 m1 476.5 m 时，面积As4为2 562 m2。

表1 仿真参数Tab.1 Simulation parameters

3 分析与讨论

在机组的甩负荷过程中，最高转速、最大水击压力、调压室最大涌浪和最小涌浪需要被重点关注，也是评估机组甩负荷过程安全性的重要指标，所以，在本节中，参数相对于这几个输出变量的敏感性将被重点分析。

3.1 转速升高

机组甩负荷过程中最高转速的全局敏感性分析结果如图4所示。

图4 最高转速的全局敏感性Fig.4 Global sensitivity of maximum speed

以甩负荷过程中的机组最高转速作为输出时，无论在变异系数为0.01 还是0.05 的情况下，机组旋转部分的飞轮力矩都是对其最为敏感的参数，其他参数的影响微乎其微。另外，对比飞轮力矩的主效应和总效应指标，可以发现在不同的不确定度下其差值都很小，即飞轮力矩对甩负荷过程中转速升高的影响也主要是通过自身的作用实现，与其他参数的交互作用对转速升高的影响可以忽略。最后，对比在变异系数为0.01 和0.05 情况下对最高转速的参数敏感性特性，发现变异系数为0.05 时上游引水隧洞面积对最高转速的敏感性要高于变异系数为0.01时的敏感性。其主要原因是，在系统变异系数从0.01 同尺度放大到0.05 时，引水隧洞面积对最高转速影响的放大尺度要高于其他参数对最高转速影响的放大尺度，从而导致不同不确定度下会出现这种差异。当然从整体的角度来说，飞轮力矩的绝对主导地位仍然不会受到威胁。总体来说，飞轮力矩对于甩负荷过程中的机组转速升高的影响最为显著。

3.2 水击压力

除了转速的升高，水击压力也是甩负荷过程中影响机组安全的关键指标。如图5所示，给出了机组甩负荷过程中最高水击压力的全局敏感性分析结果。

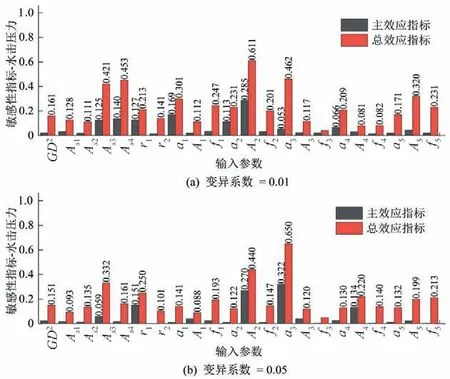
图5 最高水击压力的全局敏感性Fig.5 Global sensitivity of maximum water hammer pressure

当变异系数为0.01 时，输入参数对水击压力敏感性的主效应指标排序为：A2>a1>As4>r1>As3>a2>a4>a3>A5>f1>f2>As1>A4>A3>GD2>f5>f3>A1>a5>As2>f4>r2；输入参数对水击压力敏感性的总效应指标排序为：A2>a3>As4>As3>A5>a1>f1>a2>f5>r1>a4>f2>a5>GD2r2>As1>A3>A1>As2>f4>A4>f3。无论是主效应还是总效应，压力钢管面积对水击压力的敏感性最为显著，且从中可以看出A2独立的影响占46.6%，与其他参数的交互效应占53.4%，也就是说A2对水击压力的独立作用和与其他参数的交互作用效果基本持平。此外，蜗壳水击波速a3，调压室面积As4和As3的总效应指标都超过了0.4，它们对最高水击压力的影响也仅次于A2。与A2的作用方式不同的是，a3、As4和As3都是主要通过与其他参数的交互作用来实现对水击压力的影响。

当变异系数为0.05 时，输入参数对水击压力敏感性的主效应指标排序为：a3>A2>r1>A4>As3>A1>A3>a4>f1>GD2>A5>As1>As4>As2>a5>a2>a1>f2>f3>f5>f4>r2；输入参数对水击压力敏感性的总效应指标排序为：a3>A2>As3>r1>A4>f5>A5>f1>As4>GD2>f2>a1>f4>As2>a5>a4>a2>A3>r2>As1>A1>f3。在这种情况下，蜗壳水击波速a3会超越压力钢管面积A2成为最敏感的参数。同时，a3独立作用对水击压力影响的占比也从变异系数为0.01 时的11.51%增加到49.54%，这也就意味着随着系统不确定度的增加，a3独立的影响会被放大。其主要原因是系统不确定度的增加会使得参数的变化范围也相应地扩大，在这个过程中，a3在偏离标准值越远时其单参数项对水击压力影响的变化程度更加显著，从而使得其独立影响的占比在不确定度增加后提升而交互效应的占比下降。此外，相比于变异系数为0.01 时的敏感性指标，As4和As3的影响在变异系数为0.05时会被削弱。值得注意的是，在变异系数为0.05时，调压室流入系数r1和蜗壳截面积A4对最大水击压力的影响会显著提升。

3.3 调压室涌浪

图6描述了机组甩负荷过程中调压室最高涌浪的全局敏感性分析结果。在变异系数为0.01 时，调压室截面积（As2、As3和As4），调压室流入系数（r1）以及引水隧洞的面积（A1）对最高涌浪较为敏感，它们之间的总敏感性排序为：As3>A1>As4>r1>As2>其他。同时，可以注意到参数As3，A1，As4和r1主要是通过它们独立的作用直接影响最高涌浪高度，而参数As2则是通过与其他参数的交互过程形成对调压室最高涌浪高度的影响。剩余的参数对调压室最高涌浪的影响则不明显。在变异系数为0.05 时，输入参数对调压室最高涌浪的总敏感性排序仍然为：As3>A1>As4>As2>r1>其他。另外，与变异系数为0.01 时的参数敏感性指标进行对比，可以发现它们之间的差异并不明显。也就是说，参数不确定性的变化对调压室最高涌浪的影响比较微弱，可以忽略不计。

图6 调压室最高涌浪的全局敏感性Fig.6 Global sensitivity of highest surge

图7给出了机组甩负荷过程中调压室最低涌浪的全局敏感性分析结果。无论变异系数为0.01 还是0.05，调压室面积As3和压力隧洞面积A1是对调压室最低涌浪影响最为显著的两个参数，而其他参数的影响则相对较小。与调压室最高涌浪的敏感性结果对比可以发现，参数A1和As4的影响会明显减小，但As3对最高涌浪和最低涌浪的影响无论在哪个不确定度下都十分显著。