轴系平行不对中对离心泵转子系统振动特性的影响
2021-09-02唐晓晨尚欢欢刘厚林
唐晓晨,尚欢欢,郭 超,董 亮,刘厚林
(1.江苏振华泵业制造有限公司,江苏泰州225500;2.江苏大学流体机械工程技术研究中心,江苏镇江212013)
0 引 言
近年来,研究学者们广泛关注离心泵振动机理、故障诊断和减振控制。转子系统是离心泵的核心部件,转子系统的动力学特性对离心泵的安全运行至关重要。当转子系统存在故障时,会诱发离心泵异常振动,严重时甚至破坏离心泵零部件结构,造成重大事故[1]。
转子系统故障的60%以上是由不对中引发的异常振动[2]。转子系统不对中现象广泛存在于离心泵机组在安装和使用过程中。不对中故障会对轴承支承产生脉冲激振力,并且转轴每旋转一周,产生2 次脉冲激振力[3]并诱发离心泵机组的异常振动。因此,研究离心泵转子系统的不对中故障特性,能够准确判断离心泵转子是否发生故障,并进行检测[4]。何宵琼[5]对轴系受到的流场脉动激励力及轴系纵振和回旋振动进行分析,得到轴系振动对泵组振动的影响规律。佟延文[6]搭建水泵振动试验台,并对转子不对中、不平衡等状态的振动信号进行分析,并查找出故障原因。陈婕等[7]通过试验和模拟对质量不平衡的离心泵转子进行振动分析,得到转子质量不平衡时故障频率为1倍频。宣元等[8]建立梅花形弹性联轴器偏角不对中的力学模型,理论分析了液压泵机组的振动特性,并通过实测结果验证了理论分析的正确性。张德胜[9]应用有限元法对高压多级离心泵转子系统的不平衡响应特性进行了研究。周劲松[10]等对转子质量偏心和不对中对水轮机振动的影响进行了研究。佟施宇[11]将流体力、不对中力、不平衡力施加到轴系上,探究对泵组振动的影响。孟凡[12]、李扬[13]等分别通过模拟和试验研究了轴流泵振动特性。
联轴器不对中,是由主动轴与从动轴的轴心线之间发生径向偏移或者偏角产生的,分为平行不对中、角不对中和综合不对中3种形式[14]。国内外学者对联轴器不对中转子系统的动力学特性进行了大量的研究,主要方法有力学理论分析法、有限元分析法和实验方法[15-17]。Gibbons[18]通过对不对中量进行分解,得到了不对中产生的力和力矩。Felipe[19]通过研究转子系统不对中现象,得到转子系统径向振动主频为2 倍频的结论。Nader Sawalh[20]通过振动检测和诊断技术研究转子平行不对中故障,从运动学的角度解释了联轴器平行不对中会产生倍频响应的特性。联轴器不对中会使转子系统的主、从动轴之间的传动比不为1,两轴之间的角速度差异会使轴系联结处产生附加弯矩和周期力,进而引发转子系统的振动[21]。轴系不对中引发的转子系统振动一般会出现在1 倍转频及其偶数倍频,并且倍频分量占比随着不对中量的增大而增大。轴系不对中转子系统轴心轨迹一般呈香蕉形、月牙形或者八字形[22]。
通过建立联轴器平行不对中力学模型,并应用Ansys 的beam188 单元实现有限元分析模型的建立;对简化后的转子系统进行瞬态动力学计算,获得不同平行不对中量时,离心泵转子系统的振动幅频特性和轴心轨迹,为离心泵机组振动特性的研究和故障监测提供参考。
1 转子系统有限元建模
选用比转速67.09 的单级单吸立式离心泵研究为对象。流量Qd=100 m³/h,扬程H=82 m,转速n=2 950 r/min。转子系统由联轴器、转轴、叶轮、轴承等组成,如图1所示。
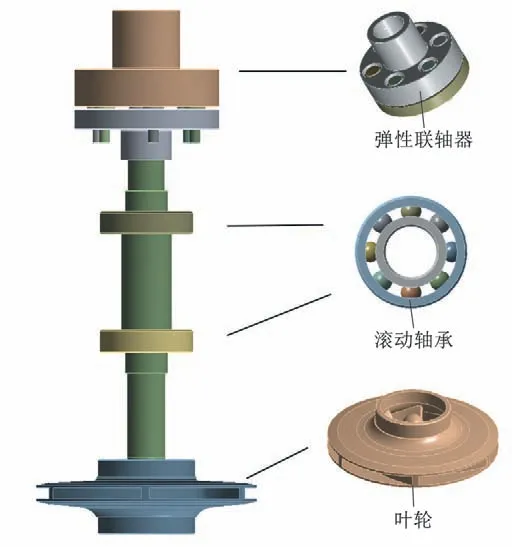
图1 转子系统模型示意图Fig.1 Model of rotor system
根据有限元法对转子系统进行简化:将转轴建立三维可变形梁单元;轴系转动部件等效为刚体,质心处集中质量和转动惯量;基座为刚性支承,轴承为弹性支承;轴系首端做简单支承处理。转子系统有限元模型如图2所示。有限元模型具体步骤如下:
(1)基于Timoshenko 梁理论,将转轴处理成既有质量又有弹性的分布质量轴段。其中,轴段1 为电机轴,轴段2~14 为泵轴。转轴材料的密度为7 750 kg/m3,弹性模量为1.93 e11Pa,泊松比0.31。轴段具体参数如表1所示。

表1 各轴段参数Tab.1 Shaft parameter
(2)对节点1 沿轴线方向的平动自由度进行约束,对节点2处设置移动副约束。
(3)为了模拟节点6、节点9 处的轴承支承,对其进行设置两个正交弹簧进行约束,其中弹簧径向刚度为6 122 222.1N/mm。
(4)叶轮质心位置为节点14,且设置质量为6.726 1 kg,x和y方向转动惯量均为2 600 000 kg·mm2,z方向转动惯量为44 708 kg·mm2。
2 转子系统动力学模型
轴系出现不对中时,会出现不对中激振力、流体非定常力以及重力。离心泵转子系统力学模型如式(1):

式中:M为质量矩阵;a为节点位移,为节点速,为加速度;C为陀螺力矩阵;Q(t)为流体非定常力;G为重力;F为轴系不对中产生力。
3 流体激振力研究
泵在运行时产生的流体激振力对转子系统的振动特性产生影响,是因为流体激振力会以交变载荷的形式作用于其转子系统。因此需要先进行离心泵流场特性的分析。
图3为离心泵水体模型。由进出口延长段、蜗壳、叶轮、泄流腔、进口弯管组成。流场瞬态计算基于CFX 软件对离心泵进行计算,提取出叶轮内表面产生的径向力和轴向力。

图3 离心泵水体模型Fig.3 Pump water model
图4示为6 个周期内,叶轮内表面所受的三方向合力。左图为径向力时域图,右图为径向力频域图。从时域图可以看出,叶轮径向力在各方向所受合力呈现周期性变化。从频域图可以看出,1APF 为径向力的主要频率同时在5APF、7APF 和11APF 也存在峰值。从轴向力时域图及其线谱图可以看出,叶轮轴向力在1BPF(1BPF=6APF)处为主要频率,同时还存在不同叶频倍频处的简谐波。
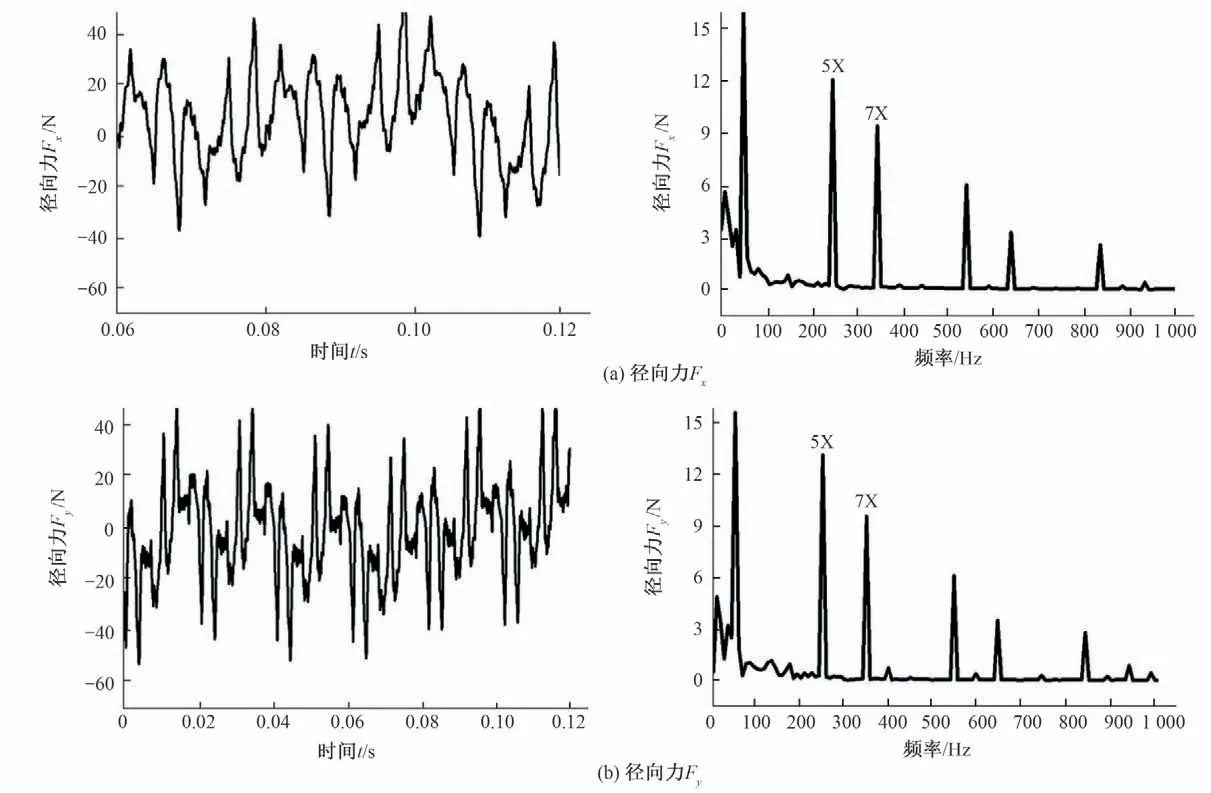

图4 流体激振力的时域图和频域图Fig.4 Time diagram and frequency diagram of fluid exciting force
为了更好地反映径向力对泵轴的作用,根据下式求解出叶轮所受径向合力F。

力的方向角:

图5为叶轮旋转稳定后所受径向力F的极坐标图。由图5可见,径向力呈周向六峰值分布,这与叶轮叶片数相对应。
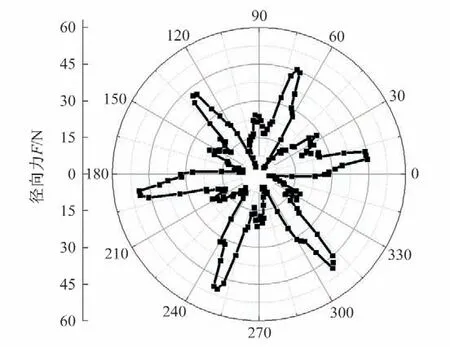
图5 径向力Fig.5 Polar coordinate diagram of radial force
4 平行不对中转子系统振动响应分析
基于Newmark 数值计算方法,对额定转速为2 950 r/min 的转子系统进行动力学分析,选取节点6、9 和14 作为监测点,对比平行不对中量在0~1 mm 范围内的振动位移线谱图和轴心轨迹,研究带联轴器平行不对中故障的转子系统振动特性。
图6、7 分别为不同平行不对中量时节点6 和节点9 的振动位移谱。可以看出,节点6 和节点9 在平行不对中状态下径向振动特征频率分别为1APF(49.16 Hz)和2APF,且1APF 为主频。轴向振动频率主频为2APF。轴向振动幅值在数量级上远小于径向振动幅值,因此可忽略轴向振动。
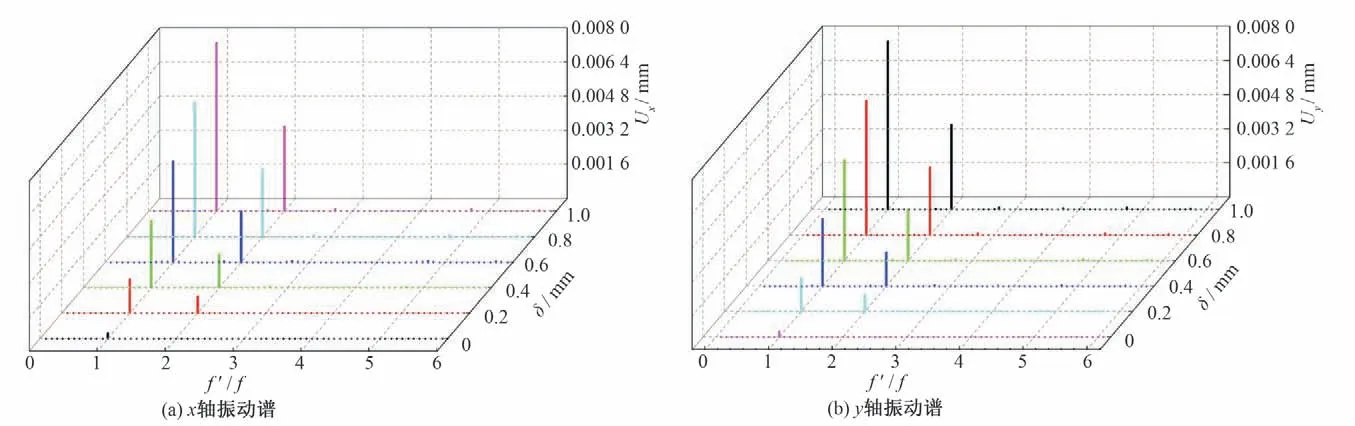

图6 节点6振动谱Fig.6 Vibration displacement spectrum of node 6
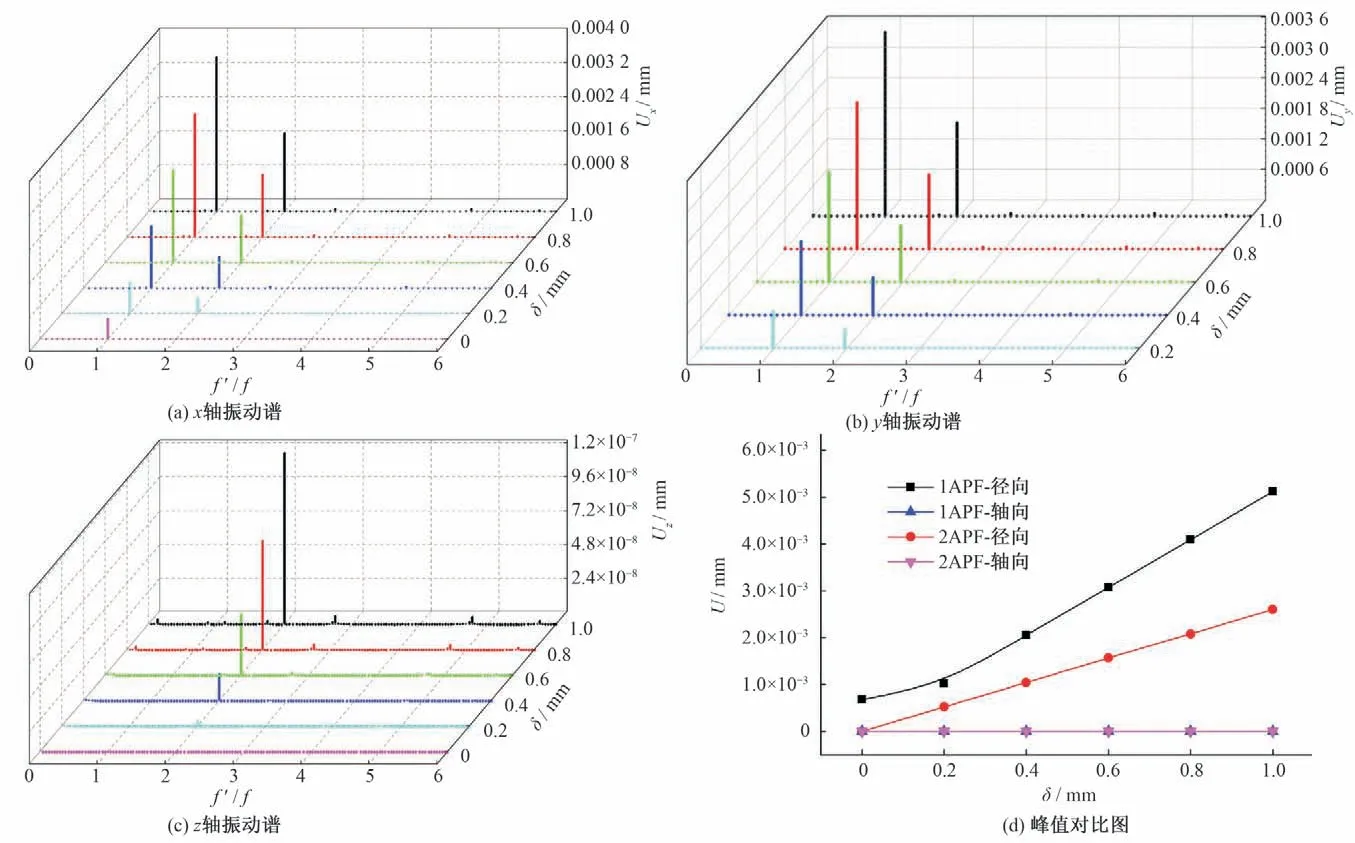
图7 节点9振动谱Fig.7 Vibration displacement spectrum of node 9
图8为不同平行不对中量δ与节点14 振动峰值对比结果。在1APF 和2APF 处节点14 有明显的径向振动峰值。平行不对中量为0时,1APF为径向振动的主要频率;平行不对中量大于0时,2APF 为径向振动的主要频率。1APF 振动位移在平行不对中量为1时为5.88×10-3mm;2APF振动位移在平行不对中量为1为6.16×10-3mm。节点14 的轴向振动主频为1BPF(1 倍叶片通过频率),轴向振动远小于径向振动,因此可忽略轴向振动。


图8 节点14振动谱Fig.8 Vibration displacement spectrum of node 14
图9为节点6、9 和14 的特征峰值对比图。随着δ的增大,各测点的特征峰值均增大。节点6 相对于其他节点,振动位移最大,是由于节点6 接近于两轴段联结处。节点14 在2APF 响应最明显,是因为节点14 处质量集中,其陀螺效应可以更好地反映平行不对中振动特性。可以看出,转子系统平行不对中在2APF 处径向振动特征明显,因此,可以通过此特征判断故障类别和故障严重程度。
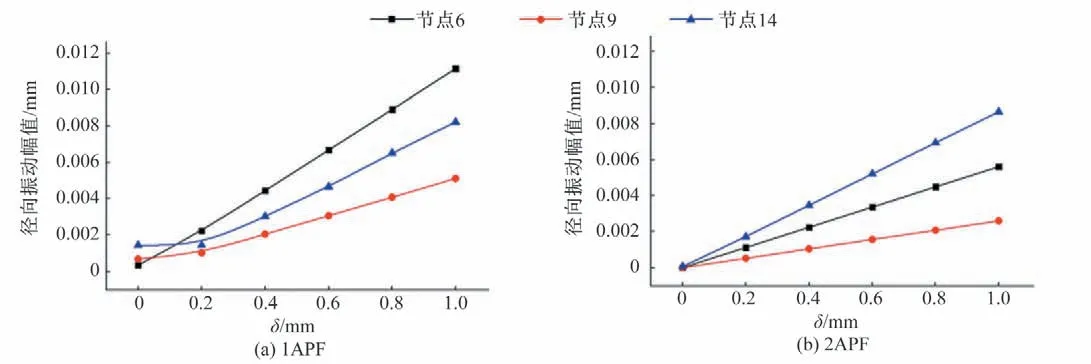
图9 各节点径向峰值对比Fig.9 Comparison of radial characteristic peaks of each node
图10为不同节点在额定转速下的轴心轨迹图。左图为理想对中下,3个节点的轴心轨迹均为光滑的圆形,表明转轴在稳定的转动。轴心轨迹在节点14 处形状最大,是因为节点14 处质量集中,惯性力最大。右图为在δ=1 mm 时的3个节点处的轴心轨迹图。平行不对中使转子系统各节点的轴心轨迹形状变为香蕉形。但各节点的轴心轨迹在多个旋转周期内形状和大小变化不大,说明转子系统在稳定旋转。因此,在离心泵转子系统故障诊断时,可以通过轴心轨迹的形状和大小判断转子故障的类型。
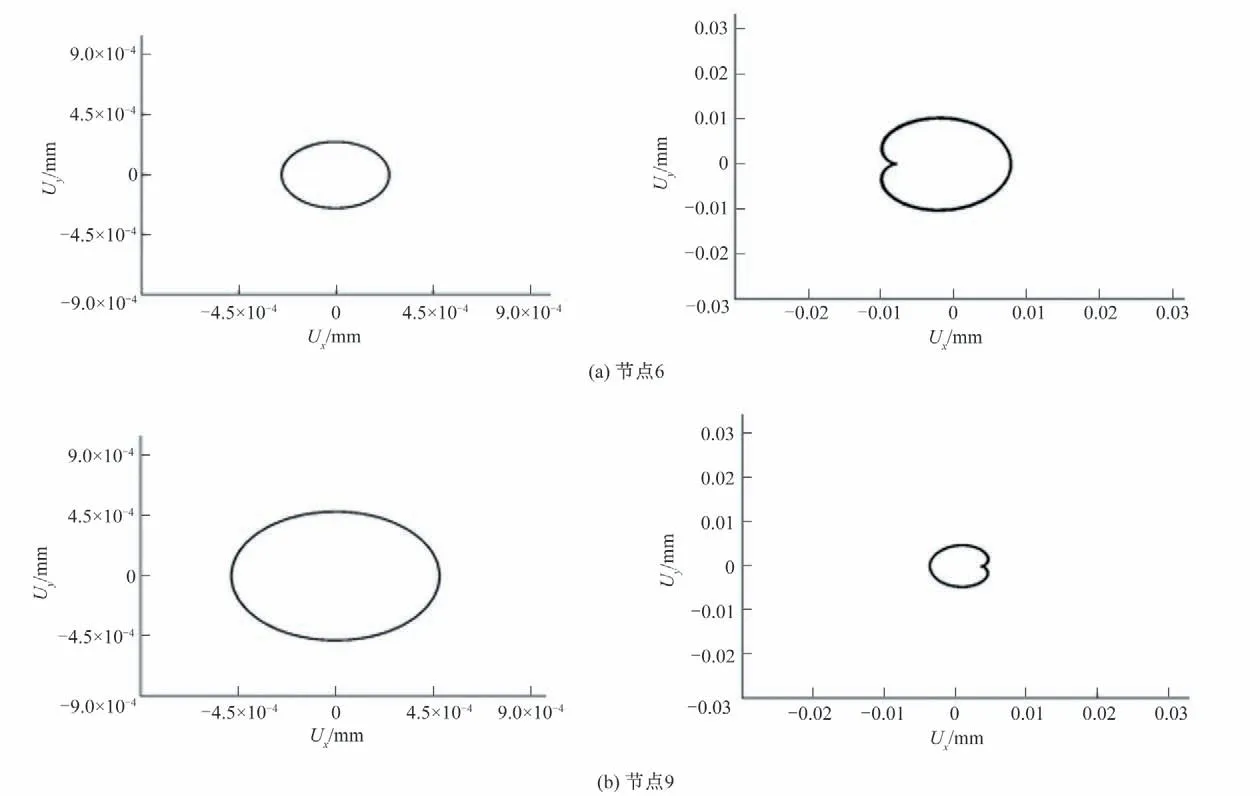

图10 不同节点轴心轨迹Fig.10 Axis trajectory
5 结 论
以立式离心泵的转子系统为研究对象,依据转子系统各组成部件的简化原理建立了平行不对中转子系统的有限元分析模型,获得了对中及不同不对中量状态下的转子系统的振动特性,为转子系统和离心泵的振动监测和故障诊断提供参考。
(1)转子系统理想对中时,径向振动最为明显,1APF 为径向振动的主要频率,1BPF 为轴向振动的主要频率,轴心轨迹为椭圆形。
(2)转子系统平行不对中时,径向振动主频为2APF,其中1APF 处也有较明显的振动。转子系统平行不对中时,轴心轨迹为香蕉形。随着平行不对中量的增大,转子径向振动位移幅值呈线性增大。□
