考虑运动补偿的机载SAR定位误差传递模型及航迹标定方法

高 铭 仇晓兰 孟大地 黄丽佳 丁赤飚

①(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)

②(中国科学院空天信息创新研究院 北京 100190)

③(中国科学院大学 北京 100049)

1 引言

机载合成孔径雷达(Synthetic Aperture Radar,SAR)具有高分辨率成像和高精度目标定位能力[1,2]，在地图测绘、国土资源勘察、灾害监测等方面有重要作用。机载SAR图像的定位误差主要受载机平台位置和速度测量误差、系统延迟测量误差等的影响。此外，载机在实际飞行中会受到气流的影响，产生运动误差，成像处理中为了得到聚焦良好的图像，通常需要进行运动补偿。由于运动误差具有随距离和方位向的空变性，运动补偿处理很难实现对每个位置目标运动误差的完全补偿，难免存在运动补偿残余误差，该残余误差不仅影响聚焦质量，也会带来定位误差。建立考虑运动补偿残余误差下的机载SAR定位误差传递模型，对于航迹测量误差的标定，进而实现弱导航信息下的高精度定位具有重要意义。

近年来已经有许多关于机载SAR定位误差的研究。其中，文献[3]分析了距离向和方位向位置、速度误差对定位精度的影响，得出了距离向速度误差是影响定位精度的主要因素的结论。文献[4]则分析了更多影响因素，给出了多普勒中心估计误差、系统时间延迟测量误差等对定位精度的影响方式。文献[5]认为各项误差对定位精度的影响近似互不相关，因此将总体定位误差近似等效为各项误差引起定位误差的均方根。上述研究大多基于匀速直线运动模型，文献[6]则进一步结合BP成像算法研究了在曲线航迹下航迹测量误差对定位精度的影响，并给出了曲线航迹下的定位误差表达式。然而，上述研究均未考虑运动误差和运动补偿处理过程，误差传递模型考虑因素不够全面。

现有机载SAR成像处理中已有很多关于运动误差补偿的研究[7,8]，但鲜有研究给出运动补偿残余误差对SAR图像定位的影响模型。文献[9]推导了机载SAR天线相位中心(Antenna Phase Center,APC)位置误差、数字高程模型(Digital Elevation Model,DEM)误差、系统时延等引起的运动补偿残余相位误差，并仿真分析了其对成像质量的影响；文献[10]在参考高程存在误差的情况下建立了运动补偿残余误差对机载双天线InSAR干涉相位的影响模型，进而分析了由干涉相位误差引入的高程和平面定位误差；文献[11]指出机载InSAR干涉图中残余运动误差的影响主要有方位相位起伏和方位配准误差；文献[12]则考虑了残余运动误差在机载重轨干涉SAR系统中导致的时变基线误差，并提出了一种估算时变基线误差的方法；文献[13]虽然给出了运动补偿残余相位误差的线性项与方位向几何定位误差的关系，但其在假设不存在航迹测量误差的情况下进行考虑。可见，现有研究主要分析了运动补偿残余误差对成像质量或干涉测量的影响，但并未给出运动补偿残余误差对机载SAR定位误差影响的解析表达式，且均未考虑运动补偿残余误差和航迹测量误差均存在的情况，不利于对定位误差影响的理解，更不利于对误差源的标定。

本文推导了航迹测量误差和运动补偿残余误差影响下的机载SAR定位误差解析模型，并进一步给出了基于该模型的航迹测量误差标定方法，得到了接近真实航迹的标定结果，证明了方法的正确性和有效性。

本文后续内容如下：第2节给出含运动误差和航迹测量误差的机载SAR信号模型；第3节推导建立运动补偿残余误差影响下的定位误差传递模型，并给出航迹测量误差标定方法；第4节进行仿真实验，验证误差传递模型和标定方法的正确性，通过对比实验证明模型的优越性，并且对定标点测量误差进行了考虑；第5节进行总结与展望。

2 机载SAR信号模型

机载SAR几何关系如图1所示。假设存在航迹误差的SAR平台只在水平方向(x轴)和高度方向(z轴)有误差，在前进方向(y轴)无误差或已通过方位重采样补偿了y轴方向的误差。载机的运动误差使实际航迹偏离理想直线，同时航迹测量误差又使测量航迹偏离实际航迹。

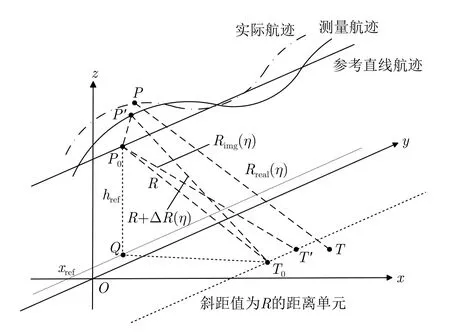
图1 机载SAR几何关系Fig.1 Airborne SAR geometry

如图1所示，P为SAR平台的实际位置，P′为对应的测量位置，P0为该时刻参考直线航迹上的对应位置；T为地面目标点的真实位置；T′为对点T成像所得的成像点位置，位于斜距值为R的距离单元；T与T′的位置差即为定位误差；T0是与T′位于相同距离单元，但方位向处在波束中心处的点。

SAR平台沿实际航迹运动并获取回波，得到T点的回波信号在距离压缩后有如下形式：

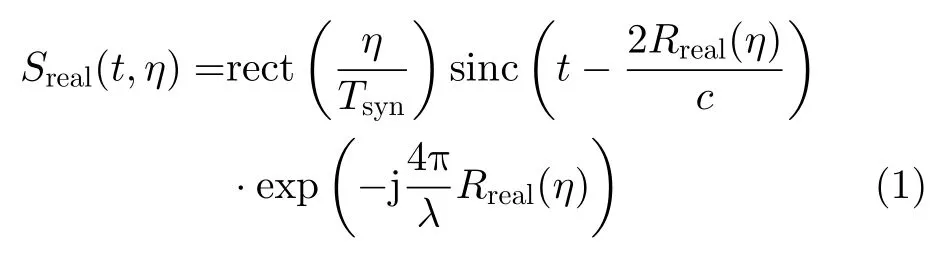
其中，t为距离向快时间，η为方位向慢时间，设T点的合成孔径中心时刻为方位向0时刻，Tsyn为合成孔径时间，Rreal(η)为实际航迹和目标点之间的距离历程。

运动误差的存在使得目标的回波信号与匀速直线运动下的信号不同，不利于Chirp Scaling,Omega-K等频域成像算法的批量处理，因此需要进行运动补偿。目前已有很多对频域成像算法和运动补偿步骤进行结合的研究[14,15]。本文使用相比于两步运动补偿[16]而言精度更高的一步运动补偿[17]方法，先根据测量航迹选择参考直线航迹，再利用测量航迹与参考直线航迹之间的偏差值对回波信号进行补偿处理。一般情况下主要考虑运动误差的距离空变性，而忽略其方位空变性[18,19]，本文对处在同一距离单元不同方位位置的目标，都采用该距离单元对应的斜距作为参考斜距进行补偿。

如图2所示，运动补偿量为视线方向的误差[20]ΔR(η)。在进行一步运动补偿时，对各个不同的距离单元补偿不同的相位。对斜距值为R的距离单元补偿如下相位

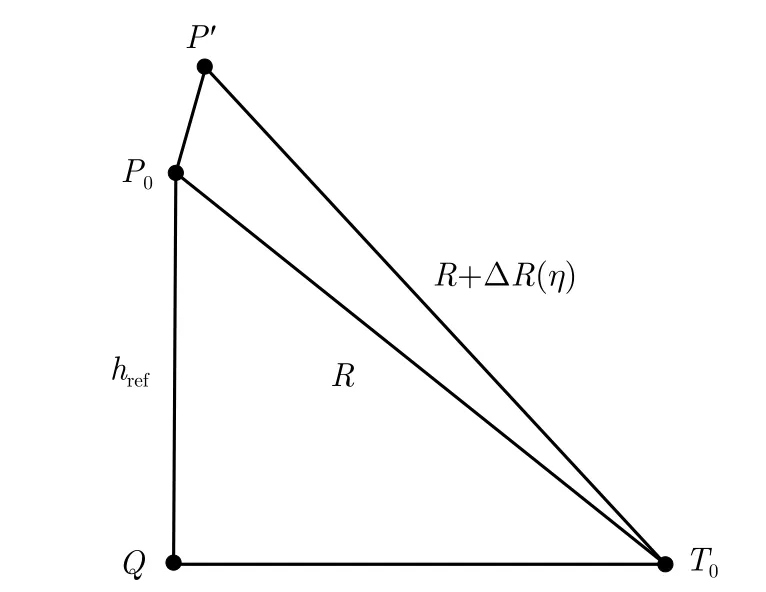
图2 跨航迹平面内的SAR几何关系Fig.2 SAR geometric relationship in the cross-track plane

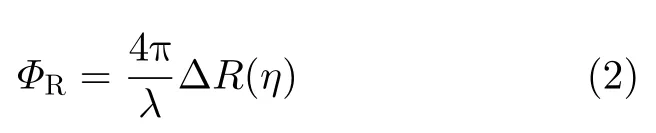
其中，ΔR(η)如下：

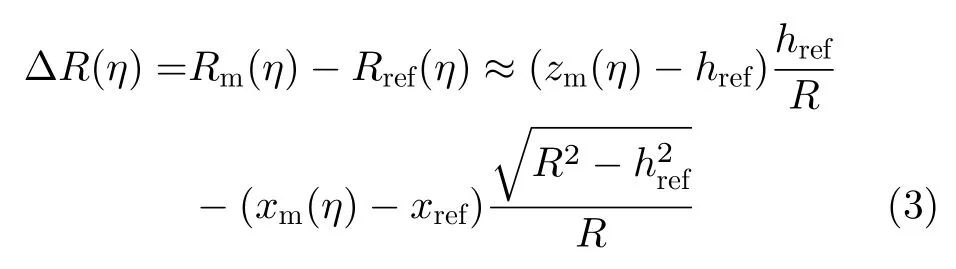
Rm(η)和Rref(η)分别表示测量航迹和参考直线航迹与目标点之间的距离，xm(η)和zm(η)分别表示测量航迹的水平和高程坐标，xref和href分别表示参考直线航迹的水平和高程坐标。

进行运动补偿后，斜距值为R的距离门对应的相位为

其中

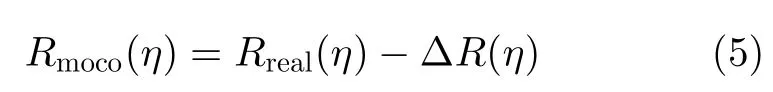
完成运动补偿后，用参考直线航迹对运动补偿之后的信号进行建模成像和基于距离多普勒模型的几何校正，得到对应的成像点T′。设该成像点与参考直线航迹之间的距离历程为Rimg(η)，根据SAR成像原理可知，该距离历程与运动补偿之后信号相位所对应的距离历程Rmoco(η)是匹配的，即

下文根据该距离历程匹配关系，推导定位误差传递模型，并得到航迹测量误差的标定方法。

3 定位误差传递模型及航迹标定方法

3.1 定位误差传递模型

为了标定整个航迹的误差，将整个航迹划分成一系列子孔径。在单个子孔径内，设机载SAR平台在前进方向(y轴)无误差，做匀速直线运动，而在水平方向(x轴)和高度方向(z轴)有运动误差。

除运动误差外，对于不可忽略的航迹测量误差，设方位向测量误差为零，主要考虑水平方向和高度方向。

测量误差设为如式(7)形式，其中包括恒定的速度误差c1,d1和位置偏移c0,d0：

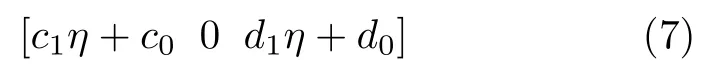
子孔径内的测量航迹用二次多项式表示为

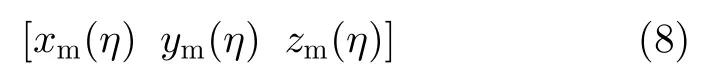
其中

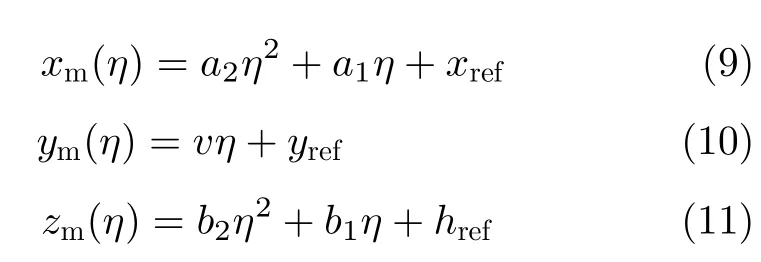
a2和b2为测量航迹关于方位向慢时间η的二次项系数，a1,v和b1为一次项系数，xref,yref和href为常数项。

真实航迹是测量航迹与航迹测量误差之间的差值，用二次多项式表示为

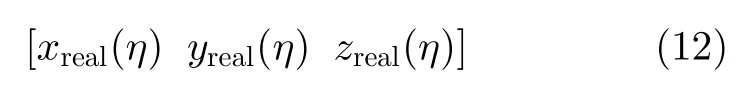
其中

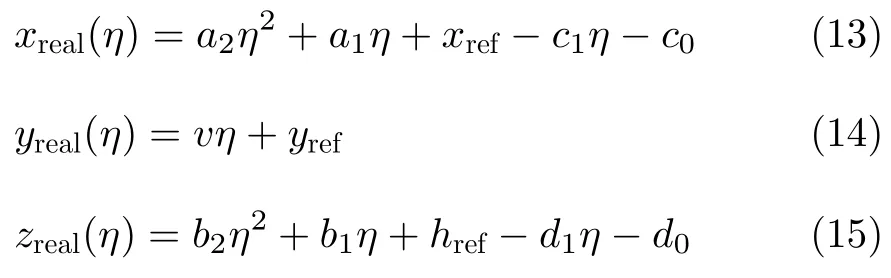
在实际中，平台的真实运动航迹是不可获得的，但测量航迹是由传感器得到的已知量。因此，运动补偿需要基于测量航迹进行。根据测量航迹选择运动补偿的参考直线航迹为

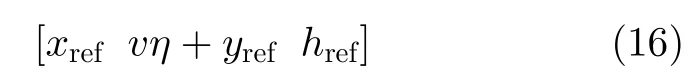
由测量航迹和参考直线，可以得出两者之间的偏差，近似为运动误差：

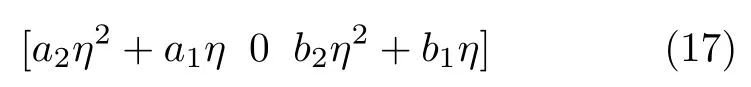
利用该误差计算视线方向误差：

将式(19)进行泰勒展开可得

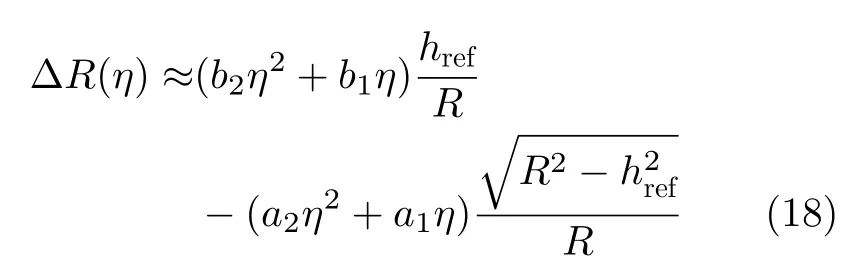
设地面目标点P=[x0y00]，其对应的成像点P′=[x0+Δx y0+Δy0],x0,y0为目标点的真实坐标，而 Δx,Δy为目标点的定位误差。

在SAR平台飞行获取回波时，真实航迹和目标点之间的真实距离历程为

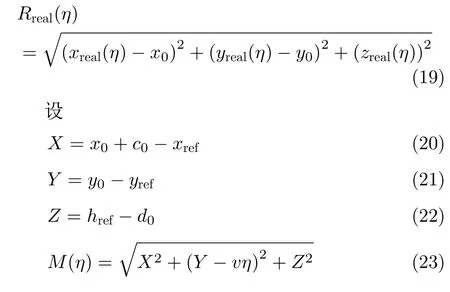
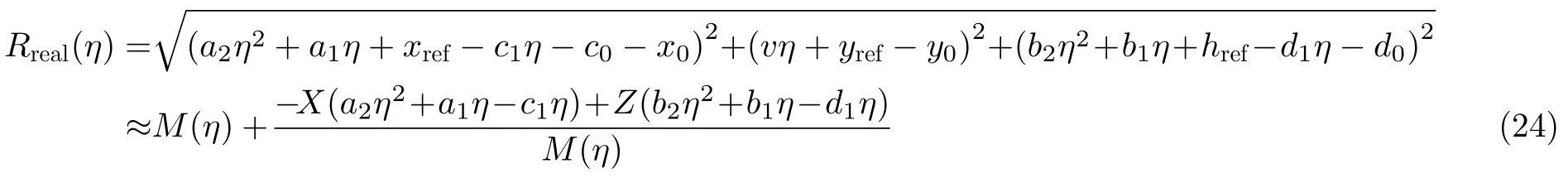
又设变量N为

对斜距值为R的距离门进行运动补偿之后的相位所对应的距离历程为

参考直线航迹和成像点之间的距离历程为

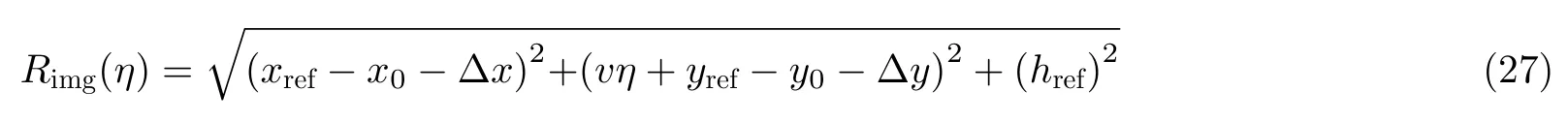
由于定位误差 Δx和Δy可能比较大，1阶泰勒展开精度不够，故对其进行2阶泰勒展开，结果为

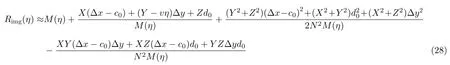
可知，式(26)和式(28)中的两个距离历程Rmoco(η)和Rimg(η)只有分式中除M(η)之外的部分形式不同。由于两个距离历程应是匹配的，其分式中除M(η)之外的部分也应尽量相等。

首先，令式(26)和式(28)的分式中除M(η)之外的部分的η的一次项系数相等，可以得到如下关系：

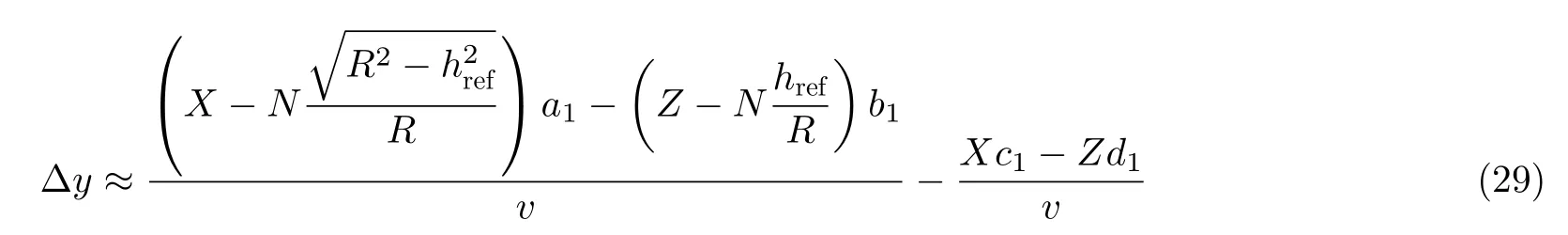
式(29)即为方位向定位误差 Δy的表达式。从式(4)可以看出，方位向定位误差受目标点自身的位置、平台的运动误差和航迹测量误差共同影响。

同理，令距离历程Rmoco(η)和Rimg(η)的分式中除M(η)之外部分的常数项相等，可得

设变量K为

整理式(30)可得定位误差 Δx的表达式为

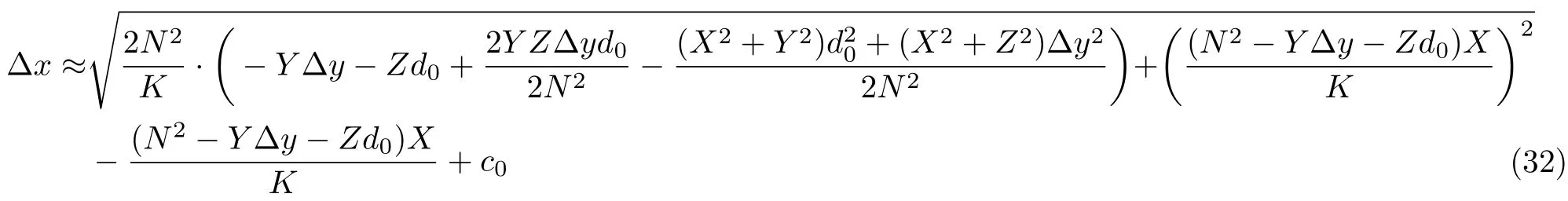
从式(32)可以看出，定位误差 Δx同样受目标点自身的位置、平台的运动误差和航迹测量误差共同影响。

3.2 航迹测量误差标定方法

推导出的定位误差传递模型不仅阐明了误差源的影响方式，同时还提供了测量误差标定的方法。由于定位误差随目标点自身位置变化而变化，因此，可以通过在地面上设置多个定标点，利用不同的定标点坐标建立多组方程进行联立，求解出公式中所涉及的测量误差，从而得到接近真实值的标定航迹。

航迹测量误差标定方法如下：

首先，标定方法中各参数在具体实现时均可获得。公式中的速度测量值、定标点坐标和测量航迹参数均可通过测量来获得，公式中的斜距值可由采样时延算得。此外，通过成像处理可以得到定标点的成像位置，利用该位置能够计算出其地理坐标，该坐标与其真实值之差即为定标点的定位误差，因此定位误差也可在具体实现时获得。

设置m个地面目标点作为控制点。首先，用各目标点坐标[x1y1],[x2y2],[x3y3]···代替式(30)中的[x0y0]建立m个等式。在这组等式中，除c0和d0以外的其他变量均已知，因此，对其进行非线性最小二乘求解，可以解出测量误差的常数项c0和d0。

将得到的c0和d0代入式(29)，并且也用各目标点坐标[x1y1],[x2y2],[x3y3]···代替式(29)中的[x0y0]建立m个等式。在这组等式中，除c1和d1之外的其他变量均已知，因此，对其进行最小二乘求解，可以解出测量误差的一次项系数c1和d1。

如此便完成了对测量误差的标定。用已知的测量航迹减去标定出的测量误差，可以得出比较接近真实航迹的标定航迹。

4 仿真实验与分析

4.1 验证定位误差传递模型

设置3个地面目标点，分别计算其实际定位误差和由所推公式算得的定位误差，比较验证定位误差传递模型的准确性。仿真参数如表1所示。

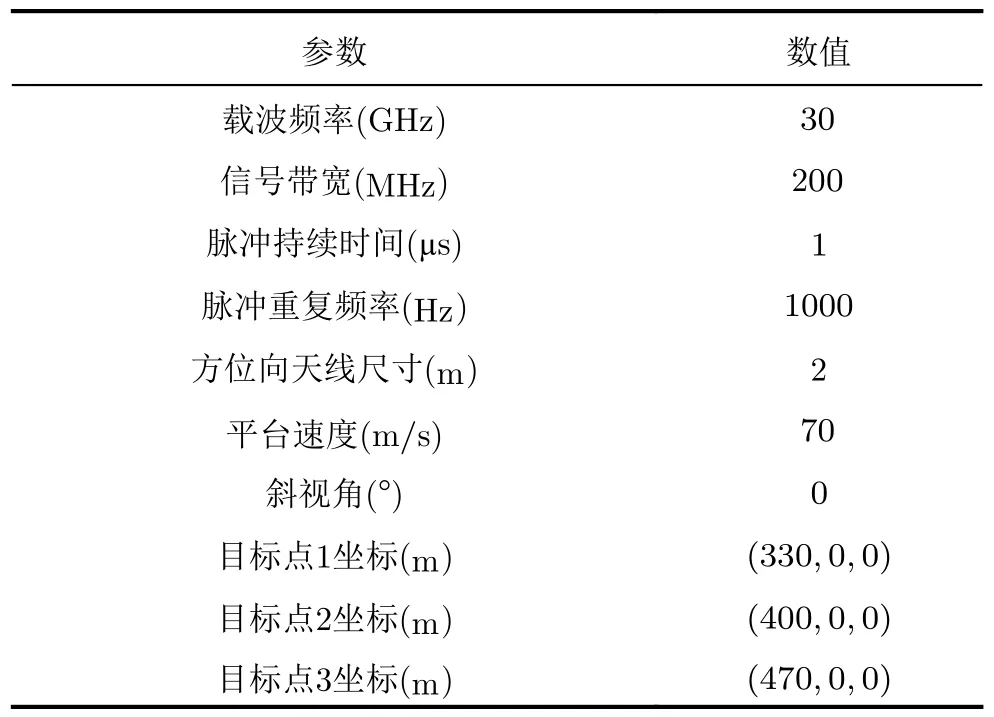
表1 定位误差仿真参数Tab.1 Simulation parameters of location error

图3给出了成像结果，红色“·”表示成像点位置，白色“ +”表示载机沿参考直线航迹飞行时点目标在图像中的位置，可见当存在运动误差和测量误差时，运动补偿和成像后目标成像结果偏离了理想位置。

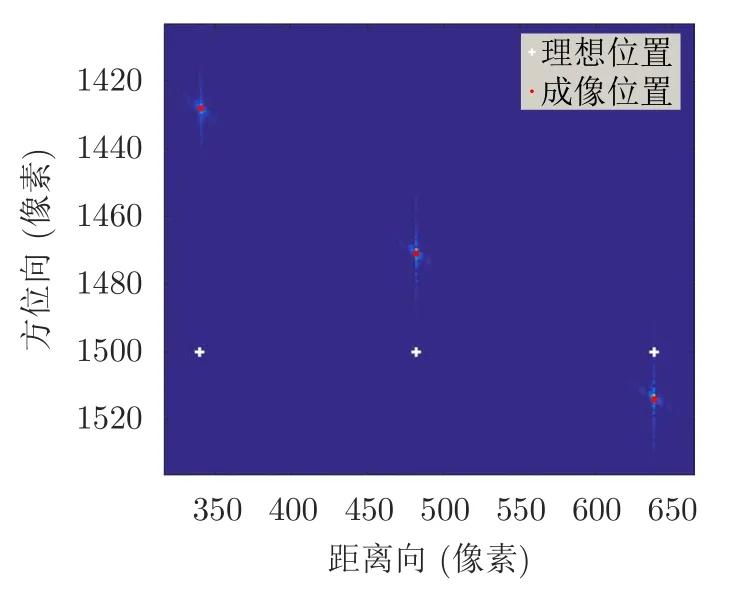
图3 成像结果图Fig.3 Diagram of imaging results

如表2和表3所示，分别在y方向和x方向计算3个目标点的实际定位误差、由定位误差传递公式算得的定位误差，以及两误差的偏差值。

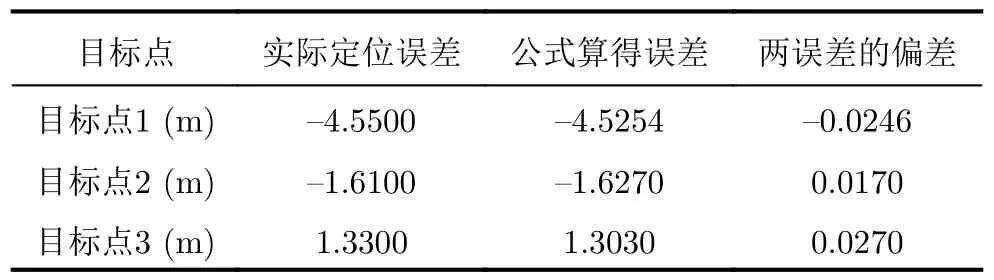
表2 y 方向定位误差Tab.2 Location error in y direction

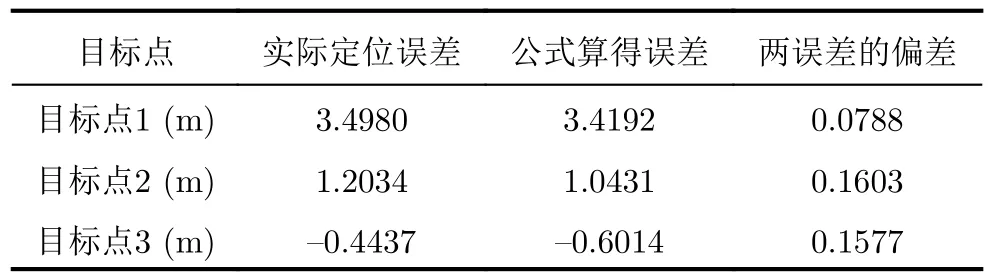
表3 x 方向定位误差Tab.3 Location error in x direction

由仿真结果可知，在y方向和x方向上，实际定位误差和由定位误差传递公式计算得到的值基本一致。仿真结果证明了本文提出的定位误差传递模型的准确性。

4.2 测量误差标定

仿真在单个子孔径内，机载SAR平台实际航迹与测量航迹的设置如图4所示，标明定标点的仿真场景如图5所示。

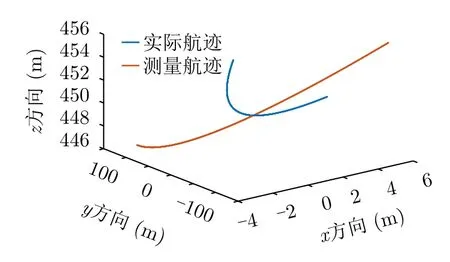
图4 航迹设置示意图Fig.4 Schematic diagram of trajectory setting

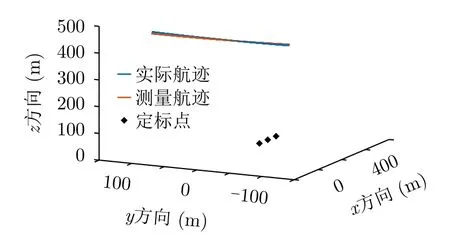
图5 仿真场景示意图Fig.5 Schematic diagram of simulation scene

x方向和z方向的测量误差标定结果以及标定航迹如表4所示。

表4 测量误差标定结果Tab.4 Calibration results of measurement error

图6为航迹标定示意图。由图6可以看出，利用该测量误差标定方法可以得到非常接近真实航迹的标定航迹。

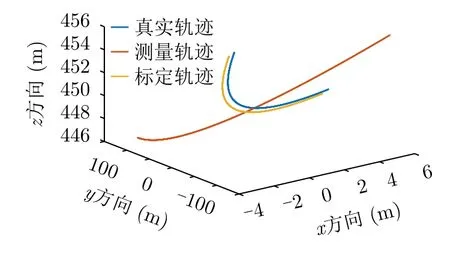
图6 航迹标定示意图Fig.6 Schematic diagram of calibration trajectory

图7为x方向航迹偏差对比图，图8为z方向航迹偏差对比图。航迹偏差指的是各条航迹与真实航迹之间的偏差。图7和图8表明，标定航迹与真实航迹之间的偏差远小于测量航迹与真实航迹之间的偏差，即证明了标定的有效性。

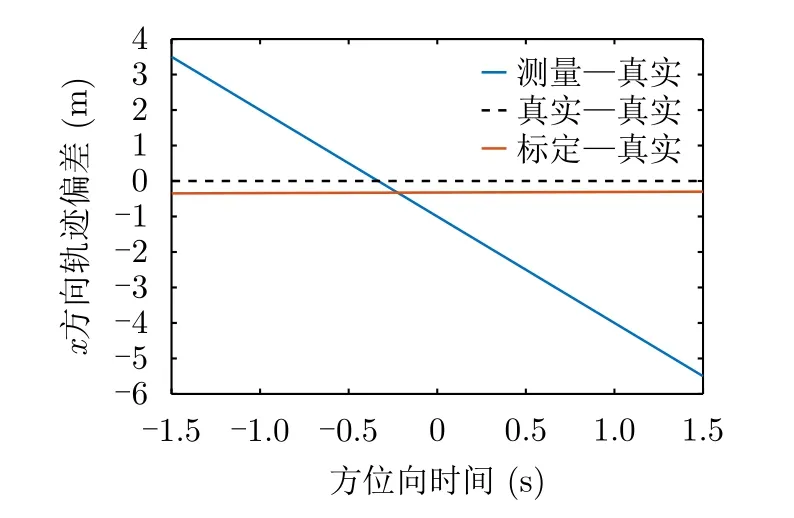
图7 x方向航迹偏差对比图Fig.7 Contrastive diagram of trajectory deviation in x direction

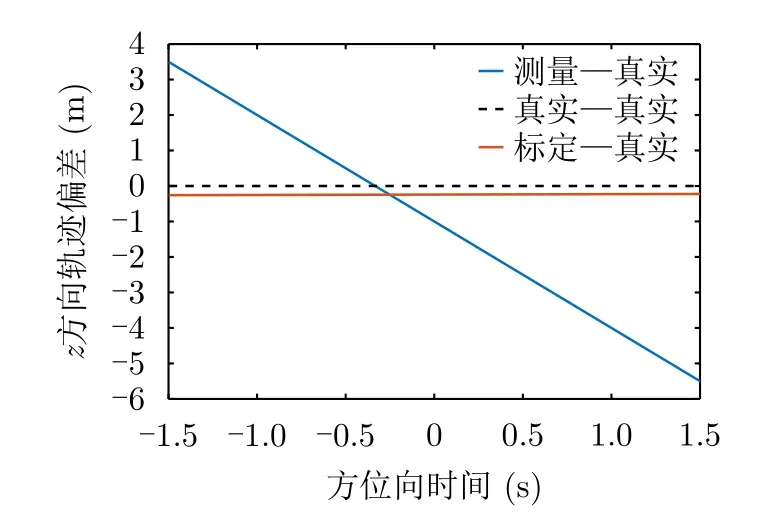
图8 z方向航迹偏差对比图Fig.8 Contrastive diagram of trajectory deviation in z direction

如图9所示，使用标定后的航迹进行成像，得到了与目标点理想位置基本重合的成像结果，该结果从另一角度验证了测量误差标定的有效性。

图9 使用标定航迹的成像结果Fig.9 Imaging results using the calibration trajectory

以上是针对单一子孔径的测量误差标定。对于整条航迹，则将其分为多个子孔径，对每个子孔径都进行上述处理。整条航迹的仿真场景如图10所示。

图10 仿真场景示意图Fig.10 Schematic diagram of simulation scene

对各子孔径的标定结果进行拟合，可得到整条航迹的标定结果，如图11所示。

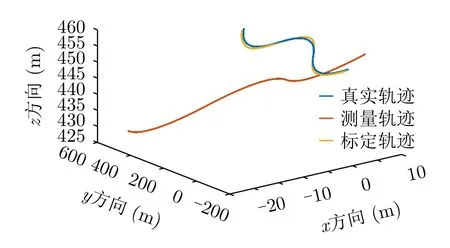
图11 整条航迹标定结果图Fig.11 Calibration result of the whole trajectory

4.3 对比实验

文献[21]对定位误差模型的推导建立在不考虑运动误差且不进行运动补偿的基础上，本文则考虑了运动误差并进行运动补偿。为验证本文模型方法的优越性，利用文献[21]模型和本文模型进行航迹标定结果的比较。

对比实验结果如下，图12为标定航迹对比图，图13为x方向整条航迹偏差对比图，图14为z方向整条航迹偏差对比图。

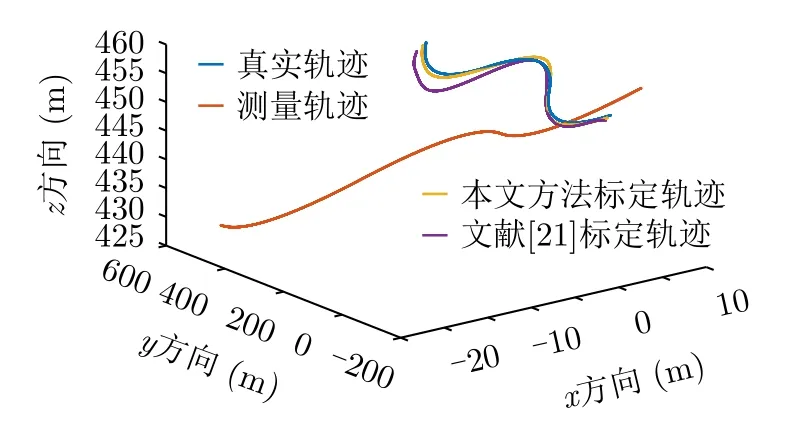
图12 标定结果对比图Fig.12 Contrastive diagram of calibration results

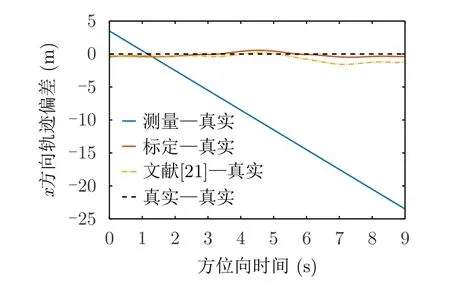
图13 x方向整条航迹偏差对比图Fig.13 Contrastive diagram of deviation of the whole trajectory in x direction

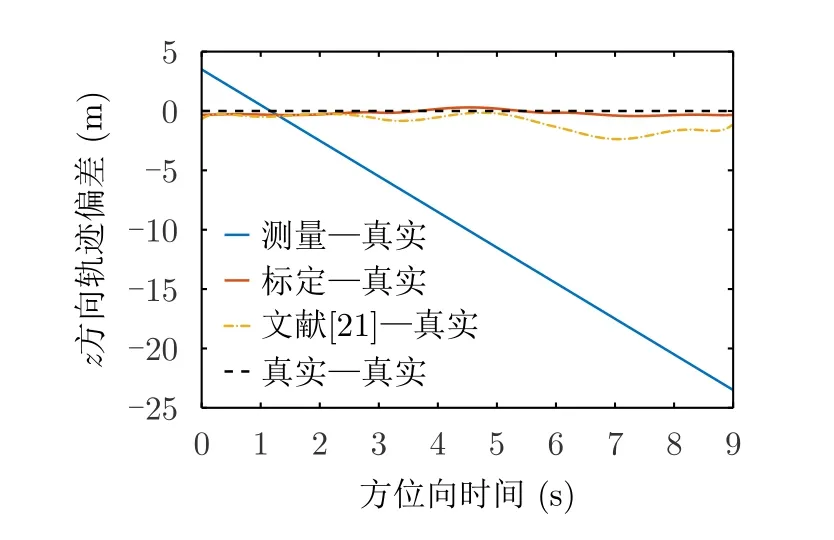
图14 z方向整条航迹偏差对比图Fig.14 Contrastive diagram of deviation of the whole trajectory in z direction

从实验结果可以看出，本文模型方法在各子孔径内均能得到较好的标定结果，效果明显优于文献[21]中不考虑运动误差和运动补偿的模型。这是因为运动补偿通常是不完全的，由于航迹测量误差的存在，根据测量航迹进行运动补偿必然会导致残余运动误差，当该误差较大时，不考虑该误差的标定模型则会表现出较差的效果。因此，提出考虑运动补偿残余误差的定位误差模型十分必要。

4.4 考虑定标点误差的实验

由于本文使用的是基于定标点的测量误差标定方法，因此需要考虑实际中存在定标点误差的情况。

首先，使用差分GPS (Differential Global Positioning System,DGPS)时的定标点测量精度可以达到0.05 m[22]。另外，由文献[23]中的式(9)可知，在带噪图像中提取点目标峰值时的精度与图像信杂比具有如下关系：

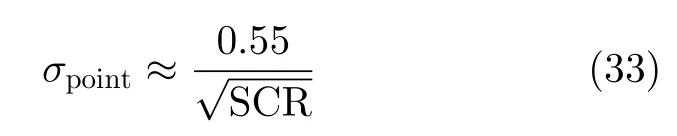
通过式(33)可以算出，在图像信杂比为15 dB的情况下，从图像上提取定标点峰值时的精度为像素。当距离门宽度为0.5 m时，距离向提取精度约为0.05 m；当方位向像素宽度为0.07 m时，方位向提取精度约为0.0068 m，远高于距离向提取精度。因此，可设定标点峰值的提取精度约为0.05 m。

根据以上对定标点测量误差的分析，可设定标点测量精度为0.1 m，进行标定实验。实验结果如表5和图15–图18所示。由实验结果可以看出，此时的定标点误差对测量误差标定结果的影响较小，与无定标点误差时的结果相近。另外，用标定后的航迹进行成像也可以得到与理想位置基本重合的成像结果。

表5 测量误差标定结果Tab.5 Calibration results of measurement error

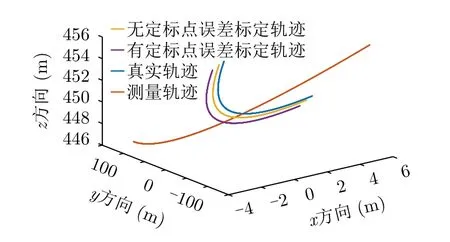
图15 航迹标定示意图Fig.15 Schematic diagram of calibration trajectory

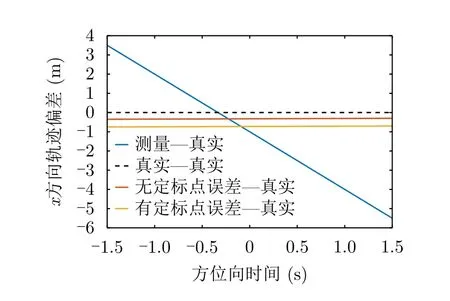
图16 x方向航迹偏差对比图Fig.16 Contrastive diagram of trajectory deviation in x direction

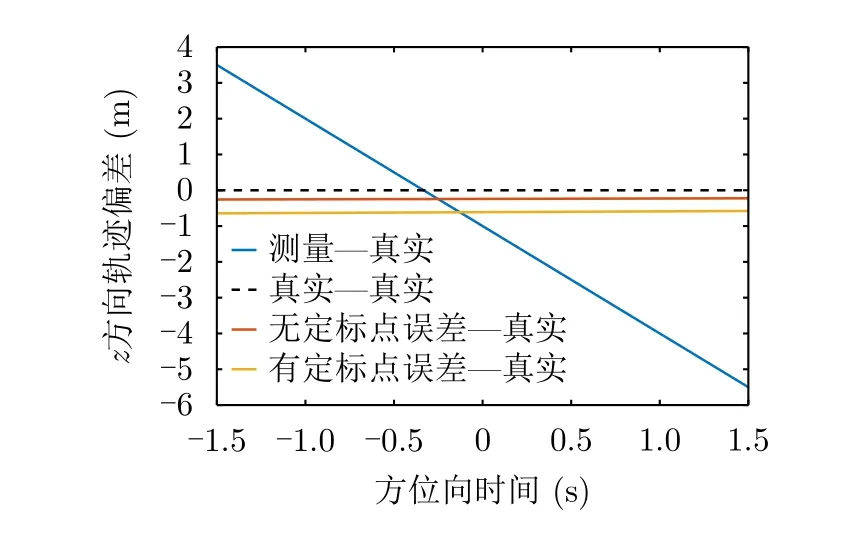
图17 z方向航迹偏差对比图Fig.17 Contrastive diagram of trajectory deviation in z direction

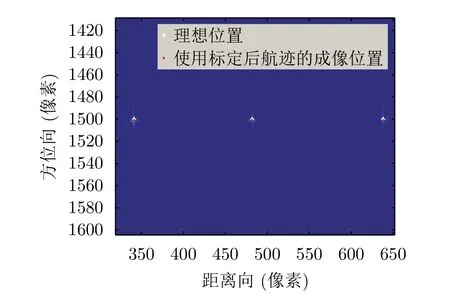
图18 使用标定航迹的成像结果Fig.18 Imaging results using the calibration trajectory

该实验结果说明，在合理的定标点误差范围内，仍可以用该定标点进行有效的测量误差标定，得到较理想的航迹标定结果。

5 结束语

本文针对实际机载SAR存在运动误差和航迹测量误差的情况，结合一步运动补偿方法，推导出了基于频域成像算法的定位误差传递模型。该模型阐明了运动补偿残余误差和航迹测量误差对定位误差的影响方式，并且提供了航迹测量误差标定的方法。文中通过仿真实验，验证了所提出的定位误差模型的正确性，并且证明了测量误差标定的有效性。同时，对比实验还证明了本文所提方法优于不考虑运动误差和运动补偿的模型，可以得到更高精度的航迹测量误差标定结果，表明了方法的优越性。此外，文中还对定标点测量误差进行了考虑。本文推导的定位误差模型可为考虑运动误差时的SAR-VIO[21]观测模型提供重要理论基础。