面向组网雷达干扰任务的多干扰机资源联合优化分配方法

张大琳 易 伟 孔令讲

(电子科技大学信息与通信工程学院 成都 611731)

1 引言

近年来，组网雷达系统(Netted Radar System,NRS)已受到了众多学者的广泛关注[1–4]。相比传统单基地雷达，组网雷达能实现多雷达的数据集成和资源共享，且不同雷达在工作方式、频段、空间覆盖范围等方面实现信息互补[2]。这些优势有利于组网雷达在电子对抗环境中实现反侦察，同时对隐身能力强的目标有更大的探测可能性[3]。因此，组网雷达具有更强的探测、跟踪、抗干扰和抗毁能力。

组网雷达已成为对抗电子干扰的重要手段，其复杂多样的组网特性使得传统的单干扰平台和一对一干扰方式即一个干扰机对一部雷达进行干扰，难以对其产生理想的干扰效果[5,6]。组网雷达给传统干扰手段带来严峻挑战，与之对抗的协同干扰技术逐渐发展起来。协同干扰是将多个干扰机进行组网，通过统一分配多干扰机的干扰时间、干扰功率、干扰样式等资源形成干扰能力更强的干扰体系，避免单干扰机在时间、功率和样式等方面的限制[5–8]。

在面向组网雷达的体系对抗中，多干扰机协同干扰更能满足干扰任务需求，也能提高目标成功突防组网雷达的概率。其中，实施协同干扰的一个关键环节就是资源分配，根据作战任务需求合理优化配置多个干扰机有限的资源，获得整个系统的最佳干扰效果。

国内外学者关于协同干扰资源调度的研究主要基于单波束干扰系统和多波束干扰系统[9–11]两大类。单波束干扰系统是指干扰机每一时刻只能产生单个波束去干扰一部雷达，而多波束干扰系统具有同时多目标干扰能力，它可以同时产生多个波束干扰多部雷达。文献[12–14]在单波束干扰系统的基础上，研究了多机协同干扰多目标的干扰资源分配问题；文献[6,15–17]是基于多波束干扰系统的协同干扰资源优化分配方法研究。上述文章提出的资源调度策略都是建立在干扰站波束发射功率均匀分配的前提条件下，通过优化波束指向实现最优干扰，均未考虑波束发射功率可控这一问题。进一步地，文献[18]针对单干扰机突防多目标的问题，提出了一种基于目标威胁等级优化分配波束发射功率的方法。文献[19]在多干扰站同时干扰多目标场景下，提出了一种基于目标威胁等级和发现概率下降程度自适应调整干扰机波束数量和波束指向的资源优化方法。

研究干扰资源调度问题还需考虑如何评估干扰策略的干扰效果，因此，选取合适的评估指标以及建立全面的干扰效果评估模型是必要的。对于压制性干扰，检测概率这一评估指标被广泛研究和应用[1,19–23]。文献[1]以雷达网检测概率作为评价指标，建立了针对干扰机编队多样式协同压制雷达网的干扰效果评估模型。文献[19]选取发现概率下降程度作为评估指标。文献[23]为提高协同干扰编队对雷达网的干扰效能，建立了基于雷达融合中心探测概率的干扰资源优化分配模型。考虑到监视雷达的首要任务是探测发现目标，因此选取雷达发现概率作为干扰性能指标是合理的。

总之，上述研究成果为提升多机协同干扰组网雷达的性能奠定了基础。但是，基于多波束干扰系统通过同时优化分配多干扰机波束和发射功率资源以提升干扰性能和资源利用率的问题还未受到关注。因此，本文针对多目标突防组网雷达的场景，提出了一种面向组网雷达干扰任务的多干扰机资源联合优化分配方法。首先，采用组网雷达在干扰环境中对目标的检测概率作为干扰性能指标；然后，结合不同目标的检测性能需求，建立了联合分配多干扰机波束和发射功率资源的优化问题，并用粒子群算法(Particle Swarm Optimization,PSO)分两步求解该优化问题；最后，考虑到组网雷达系统参数不确定性带来的检测概率泛化误差，建立了干扰资源稳健优化分配模型。仿真结果验证了本文所提资源优化分配方法以及稳健优化分配方法的有效性。

2 系统模型

2.1 系统配置及约束

假设Q个目标执行突防组网雷达的任务，组网雷达系统由N部相控阵雷达组成。为提高目标成功突防的概率，M(M ＜N)个干扰机伴飞目标同时对组网雷达实施随队协同干扰，降低组网雷达对己方目标的探测跟踪性能。多机协同干扰的前提是已获得敌方各雷达的参数(如雷达位置、载频、脉宽、重频等)，这些参数一般是通过电子侦察系统截获雷达发出的电磁信号，然后对其进行识别、分析和定位得到[24]。

在图1所示的多目标突防组网雷达二维场景中，雷达i(i=1,2,···,N)的位置为(xi,yi)，目标q(q=1,2,···,Q)在k时刻的位置和速度分别为和干扰机m(m=1,2,···,M)在k时刻的位置和速度分别为

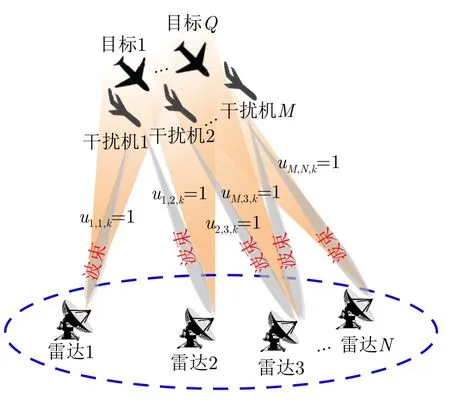
图1 多目标突防组网雷达二维平面图Fig.1 The 2D plane map of multiple targets penetrating the NRS

假设干扰机均采用多波束干扰系统[9–11]，它可以产生多个功率可控的波束同时干扰多个雷达节点，但每个波束只能干扰一部雷达。考虑到波束指向的问题，本文引入干扰机m在k时刻的波束指向向量其中，[]T表示转置运算，二元变量满足

式(2)表示每个干扰机最多分配一个波束去干扰同一部雷达。受系统限制，每个干扰机最多产生L个波束，即

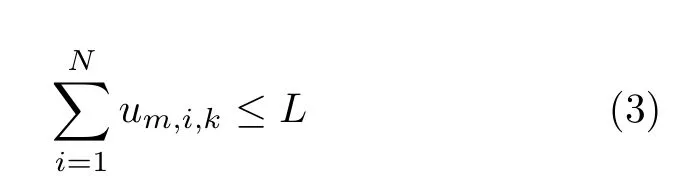
为保证干扰波束资源被充分利用，所有雷达节点均能被干扰，因此分配给每部雷达的波束个数不超过S，即

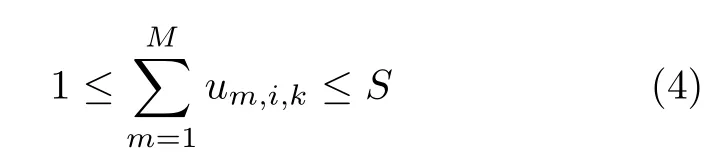
为了表示每个波束的可控发射功率，进一步定义干扰机m的波束发射功率向量Pm,N,k]T，其中变量Pm,i,k是波束um,i,k对应的发射功率，且满足

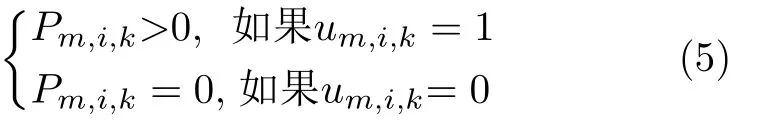
式(5)表示如果干扰机m分配波束干扰雷达i，则此波束的发射功率Pm,i,k不为0；反之Pm,i,k=0。每个波束的发射功率有最大功率Pmax和最小功率Pmin约束

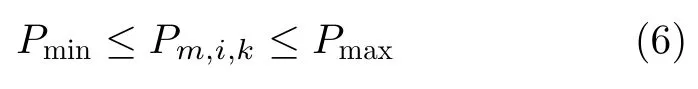
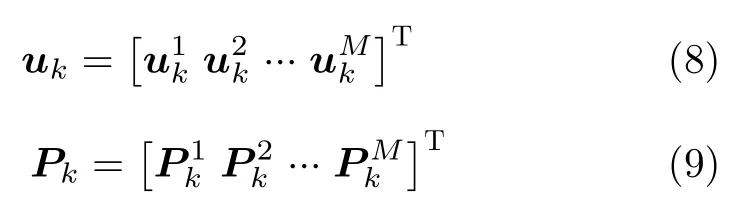
2.2 干扰信号模型

雷达干扰是指干扰机通过发射干扰信号影响敌方雷达的检测、跟踪等性能，干扰分为压制性干扰和欺骗性干扰两种类型。协同压制干扰是多个干扰信号在雷达接收机处叠加，破坏雷达检测目标信息，起到联合干扰的效果。

本文主要采用噪声调频干扰，干扰机m对雷达i施加的噪声调频干扰信号如式(10)所示。

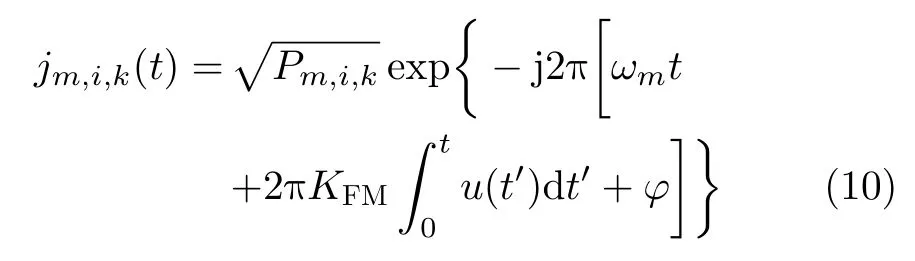
其中，u(t)为调制噪声；φ为相位函数；干扰信号振幅；ωm为中心频率；KFM为调频斜率。式(10)可变形为

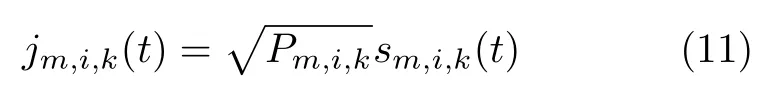
其中，sm,i,k(t)是干扰信号的归一化复包络。

2.3 雷达回波信号模型

假设雷达采用自发自收的工作模式，它只会接收和处理自身发射并经目标散射的回波信号，且每部雷达在k时刻能发现我方的Q个突防目标，那么雷达会接收到Q个目标的回波信号。在协同压制干扰条件下，雷达还会接收到多个干扰机发射的干扰信号。因此，雷达i的回波信号模型为

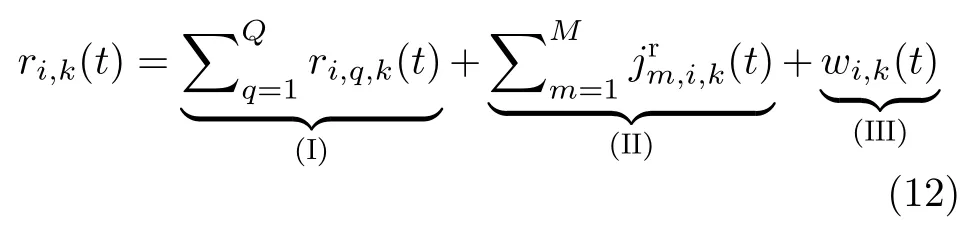
式(12)可以分为3部分，分别表示为

(I)Q个目标的回波信号：ri,q,k(t)是雷达i接收到目标q的回波信号

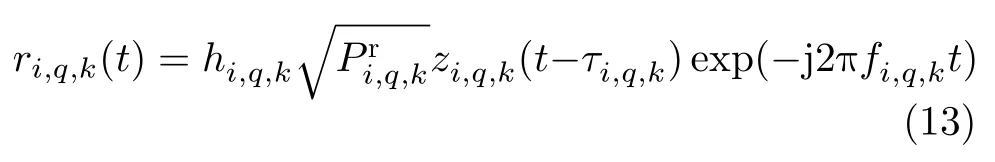
其中，hi,q,k是目标q的雷达横截面积；zi,q,k(t)是雷达发射信号的归一化复包络标q与雷达i之间的距离导致的时延；fi,q,k是目标运动产生的多普勒频移；是雷达i接收到目标q的回波信号功率[25,26]，具体为

当干扰机实施随队干扰时，由于干扰机与目标空间位置分离，随队干扰信号既可以从雷达天线的主瓣进入雷达接收机(即主瓣干扰)，也可以从雷达天线旁瓣进入(即旁瓣干扰)。雷达天线具有定向辐射的特点，式(16)中天线增益一般由经验公式给出[27,28]。

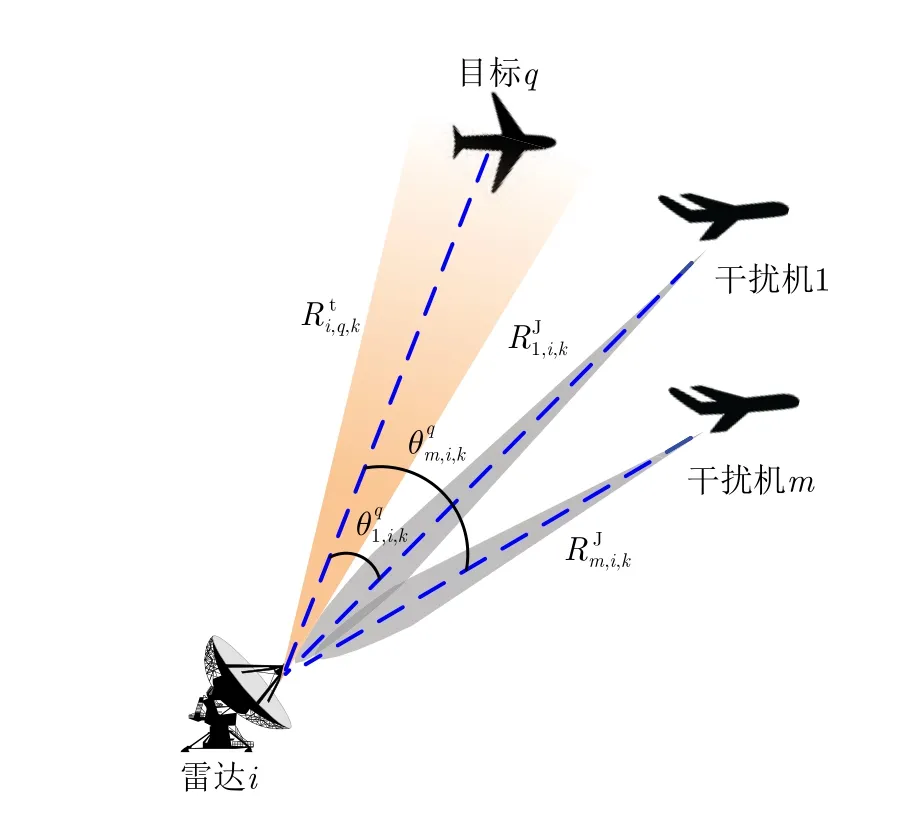
图2 干扰机、雷达和目标的空间位置关系Fig.2 Relative geometry position of the jammer,radar and target

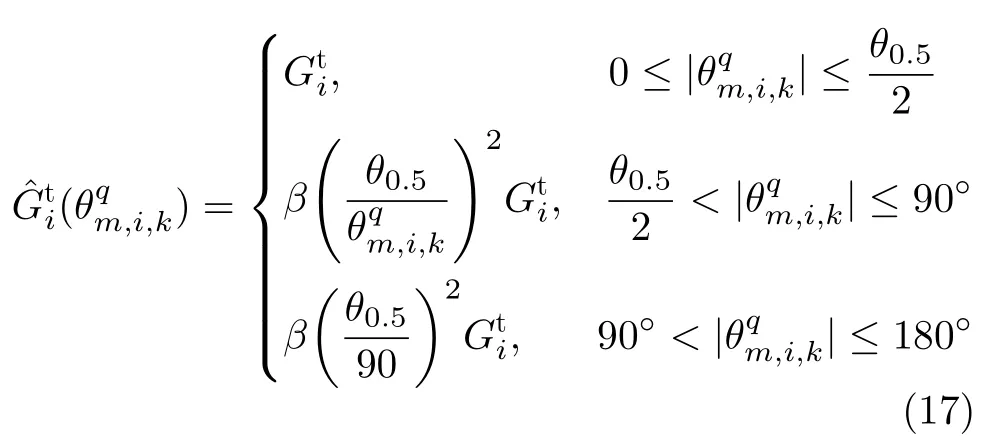
其中，θ0.5为雷达天线波束宽度；常数β通常取0.04～0.10。对于高增益、窄波束的天线，β 2[0.07,0.10]；对于低增益、宽波束天线，β 2[0.04,0.06]。

(III)wi,k(t)是雷达接收机本身产生的噪声。雷达接收机的热噪声功率一般为

其中，Pn是接收机内部热噪声功率；k是玻尔兹曼常数；T0是雷达接收机的有效噪声温度；Bn是接收机带宽；Fn是接收机的噪声系数。

2.4 协同压制干扰功率合成模型

假定各干扰机发射的干扰信号之间相互独立，当M个干扰机协同压制干扰单部雷达时，雷达接收的干扰信号总功率相当于各干扰信号功率之和。根据功率叠加原则，雷达i在 探测目标q时接收到的总干扰信号功率

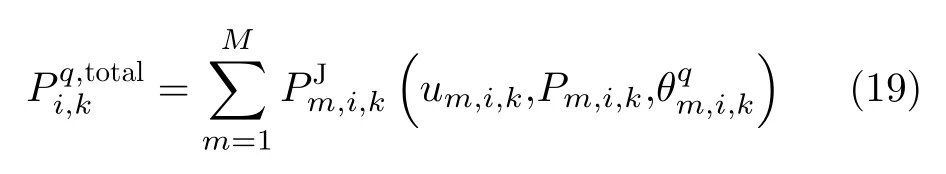
3 协同压制干扰组网雷达性能指标

3.1 协同压制干扰单部雷达检测概率模型

考虑到压制干扰的本质是使目标回波信号湮没在干扰信号中，降低雷达对目标的检测概率，且检测概率被众多学者用作衡量压制干扰性能的指标。因此，本文选取组网雷达对目标的检测概率作为干扰性能指标。本文计算检测概率是在假设电子侦察系统已获得敌方各雷达概略位置、部分工作频率与信号形式等参数信息，且不考虑单雷达欺骗干扰机的诱饵脉冲等变化情况。

在无干扰情况下，雷达i接 收端的目标回波信噪比为

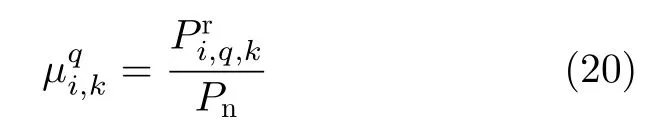
当雷达i受到压制干扰时，结合式(16)和式(19)可以计算目标q回波信干噪比为

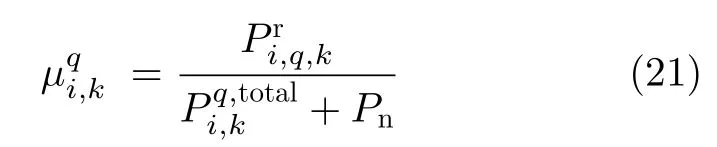
由雷达检测原理可知，在背景噪声的统计分布以及目标起伏类型已确定的前提下，根据目标回波信干噪比可以计算雷达对目标的检测概率。我们以Swerling I型目标为例，计算雷达i对目标q的检测概率[29,30]。

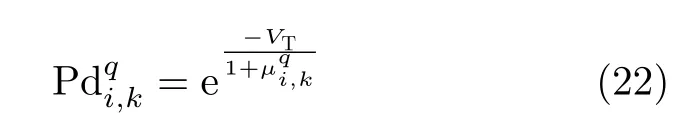
其中，VT是检测门限值。将(16)和式(19)代入式(22)可得

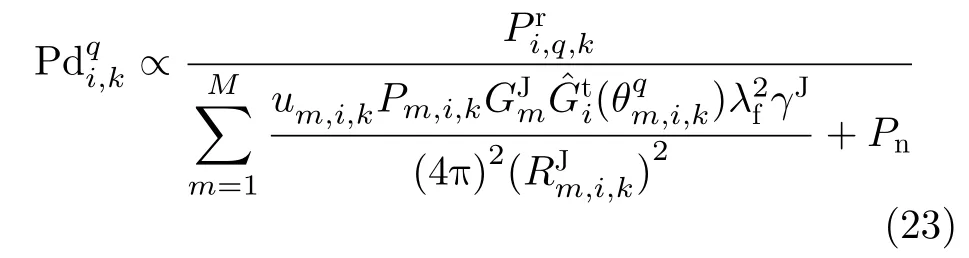
3.2 协同压制干扰组网雷达检测概率模型

考虑到在实际干扰作战中难以获知组网雷达的融合方式，本文假设组网雷达采用检测0/1信号融合方式，且组网雷达对目标检测概率的融合采用决策融合结构模型，融合中心采用K-N准则(也称秩K准则)。其具体内涵是：组网雷达中发现目标q的雷达节点数超过检测门限K(1≤K ≤N)时，就判定组网雷达发现目标q，否则判定未发现目标，如式(24)所示[31,32]。

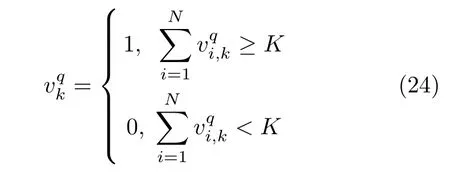
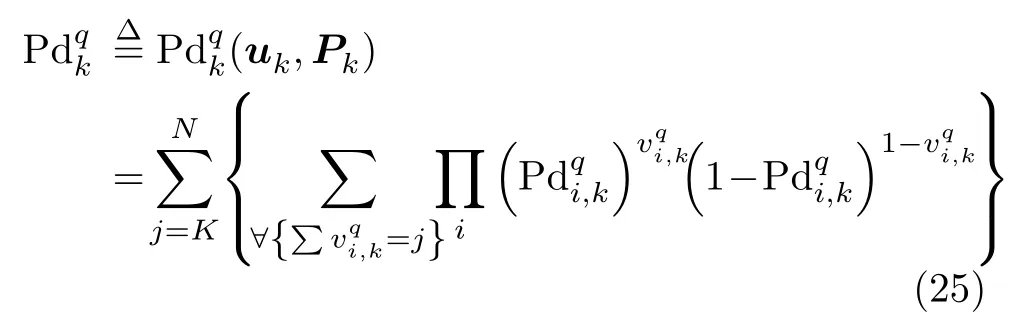
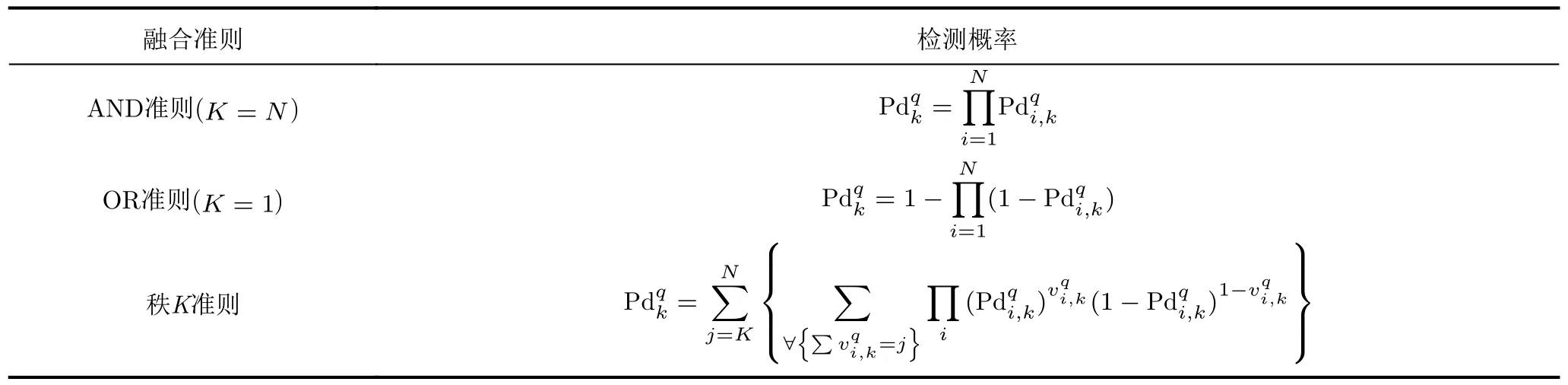
表1 不同融合准则下的组网雷达检测概率Tab.1 The detection probability of the NRS with different fusion rules

需要注意的是，本文后面建立的多干扰机资源联合优化分配模型在其他融合方式下也适用，只需根据不同的融合方式及融合准则修改检测概率模型即可，模型兼容性好。

3.3 协同压制干扰组网雷达的全局性能指标

组网雷达对Q个目标的检测概率形成的矢量Pdk，可作为多干扰机协同压制干扰组网雷达的性能评估指标如式(26)所示。

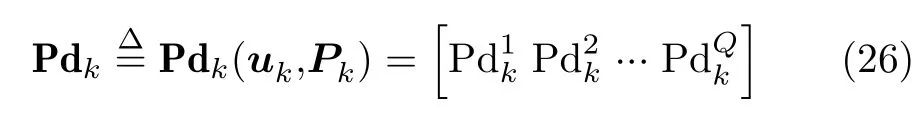
考虑到实际突防过程中，由于目标重要程度的差异，每个目标的检测概率需求会有所不同。多目标的检测概率需求矢量如式(27)所示。

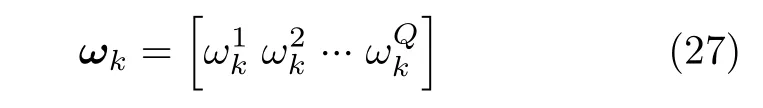
面向组网雷达干扰任务的多干扰机资源联合优化分配问题的本质是优化一个反映整体协同压制干扰任务有效性的全局代价函数。基于QoS原理[33]，本文结合Pdk和ωk建立了全局代价函数。

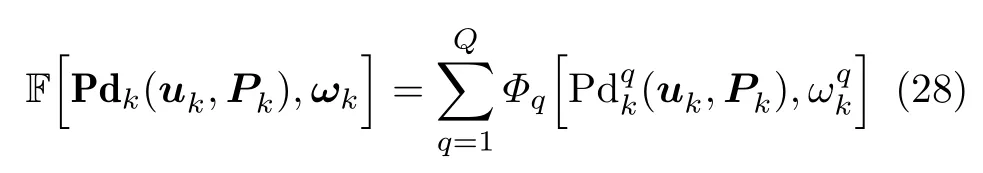
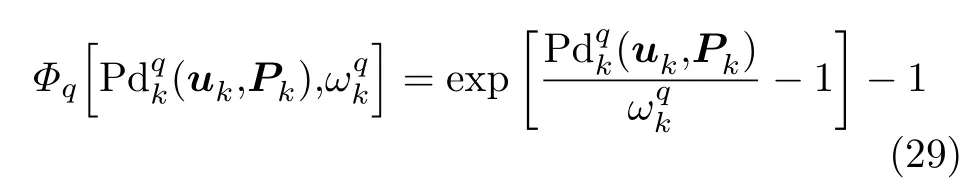
4 多干扰机资源联合优化分配算法

4.1 干扰资源优化分配模型

从干扰系统设计来说，不考虑波束指向和发射功率调度虽简单易行，但当干扰资源有限时，资源的不合理配置会造成资源利用率低，甚至会造成干扰效果不理想。本文所提的面向组网雷达干扰任务的多干扰机资源联合优化分配方法旨在干扰资源有限的条件下，通过联合优化配置多干扰机的波束和功率资源，最小化组网雷达对突防目标的检测概率，其优化模型可建立为

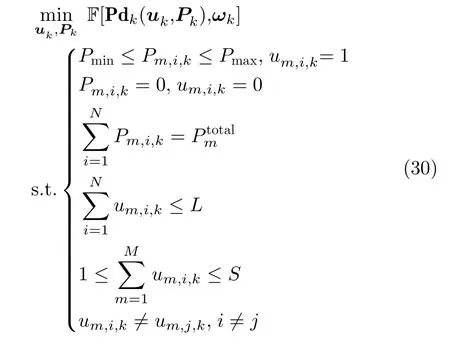
从式(30)可以看出，本文实际建立了一个带干扰资源约束条件的数学优化问题。约束1和约束2表示波束和发射功率是相互耦合的；约束3表示每个干扰机有总功率限制；约束4表示每个干扰机产生的波束个数不超过L；约束5表示每部雷达均能被干扰，且最多受到S个波束的干扰；约束6表示每个干扰机在干扰同一雷达节点时最多分配一个波束。

4.2 求解干扰资源优化分配模型

式(30)优化问题由于以下原因很难得到其最优解：(i)含有二元变量um,i,k 2 f0,1g，故它是非凸的；(ii)波束指向变量um,i,k和发射功率变量Pm,i,k是相互耦合的，且两者总是以乘积的形式出现，同时求解比较困难。于是本文提出了基于粒子群算法(Particle Swarm Optimization,PSO)的两步求解方法，具体步骤如下：

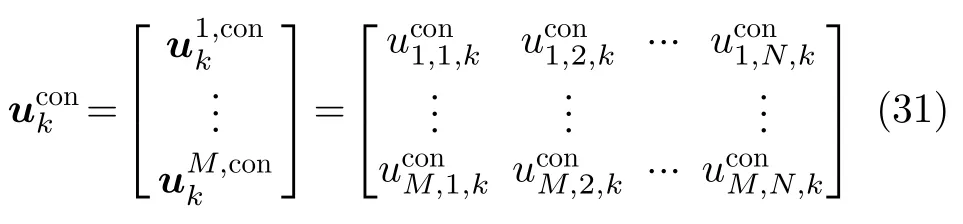
结合式(31)，优化问题变为

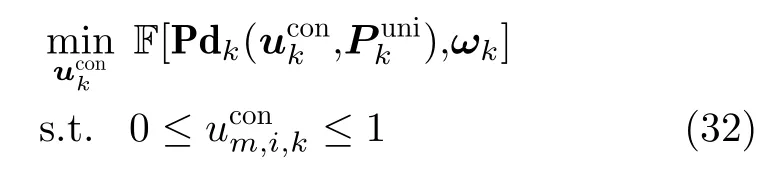
表2 基于PSO的波束指向求解方法Tab.2 The solution algorithm of the beam selectionbased on PSO

表2 基于PSO的波束指向求解方法Tab.2 The solution algorithm of the beam selectionbased on PSO

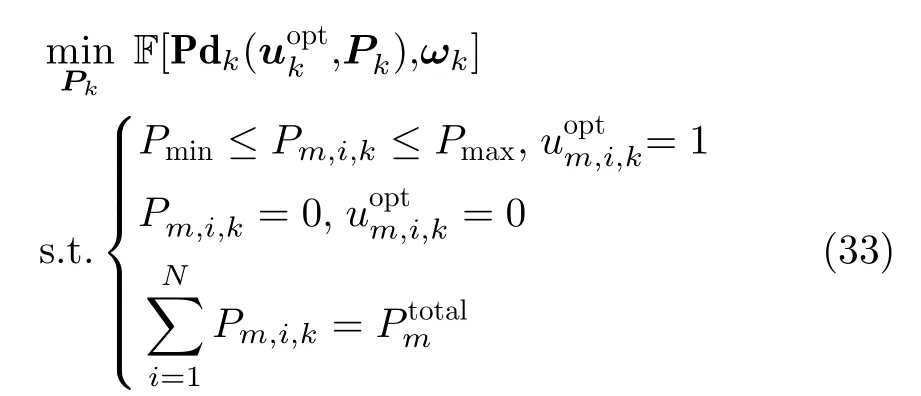
4.3 组网雷达参数不确定性模型

4.1 节干扰资源优化分配模型是建立在完全获得组网雷达系统参数的理想情况下，但实际干扰作战中，电子侦察系统一般无法精确获得组网雷达系统的各雷达位置等参数信息，同时难以获得组网雷达的融合方式以及融合准则，只能利用参数估计。受限于参数估计精度，3.1节和3.2节计算得到的检测概率相比目标真实检测概率存在泛化误差，前面提出的优化分配算法可能会出现性能下降问题。因此，本节考虑了组网雷达参数不确定性，并提出了干扰资源稳健优化分配算法。

首先考虑雷达位置不确定性，雷达i的不确定位置在一个不确定性区域内，假设将此不确定性区域表示为如图3所示的不确定性圆。

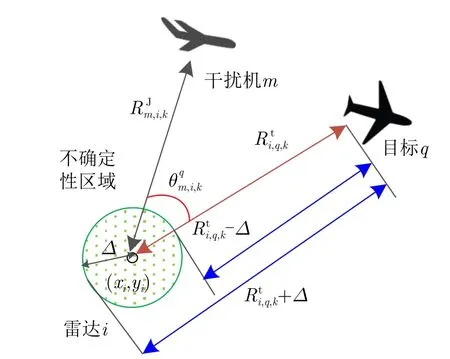
图3 距离和角度不确定性区域Fig.3 The uncertainty area of distance and angle

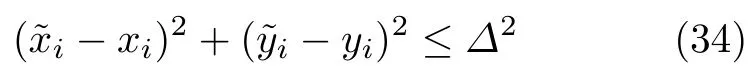
雷达位置不确定性会带来距离不确定性，距离不确定性受限于整个不确定性圆，其可以表示为线性不确定区间。

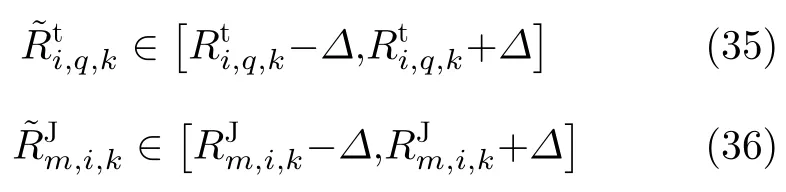
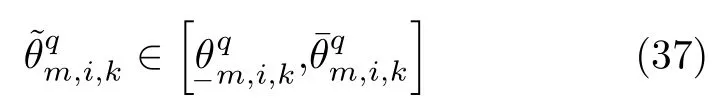
由表1知，组网雷达在不同K-N融合准则下对目标的检测概率也是不同的，所以还应该考虑融合准则不确定性，将其建为一个集合

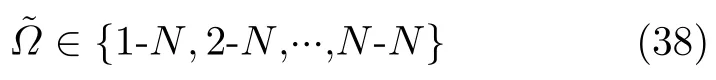
整个组网雷达系统参数不确定性可表示为

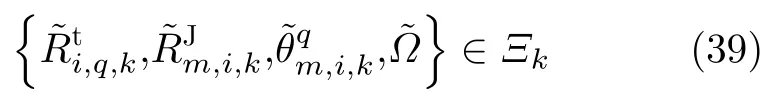
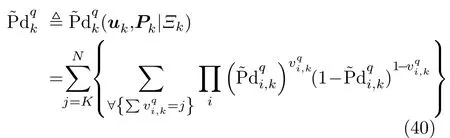
4.4 干扰资源稳健优化分配模型

基于组网雷达参数不确定性的干扰资源稳健优化分配算法，旨在提高干扰系统在组网雷达参数不确定情况下的协同干扰性能。结合已有的最大最小化准则[34,35]，稳健分配等效于最小化最差参数时的目标检测概率，确保在参数最差时多干扰机也能有效压制组网雷达。数学上可将稳健分配表述为最小化最大的

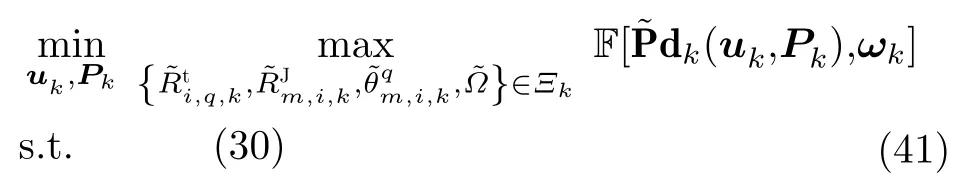
5 仿真结果与分析

本节通过仿真实验将本文算法与传统算法、稳健算法进行比较，验证本文所提方法的有效性。传统方法是所有干扰机采用单波束干扰系统且资源配置方式固定，即干扰机1干扰雷达1，干扰机2干扰雷达3，干扰机3干扰雷达5。稳健算法仅考虑雷达2位置不确定性带来的距离不确定性其中不确定性圆的半径Δ=0.5 km。

考虑Q=2个目标突防组网雷达系统，M=3个干扰机实施随队干扰。假设已知组网雷达系统由N=6部雷达组成，融合中心采用秩4准则。每个干扰机和每部雷达的参数均相同，分别如表3和表4所示。目标RCS均为hi,q,k=1 m2，检测概率需求为ωk=[0.40.4]。干扰机波束发射功率的上下限分别利用PSO求解式(32)和式(33)时，相关参数设置：粒子数为100，总迭代次数为30，学习因子均为2，在第κ次迭代时惯性权值ϖ=0.9-0.5∗(κ/50)。多干扰机随队干扰保护目标突防的运动轨迹和组网雷达的空间位置关系如图4所示。

表3 干扰机工作参数Tab.3 The working parameters of the jammer

表4 雷达工作参数Tab.4 The working parameters of the radar node

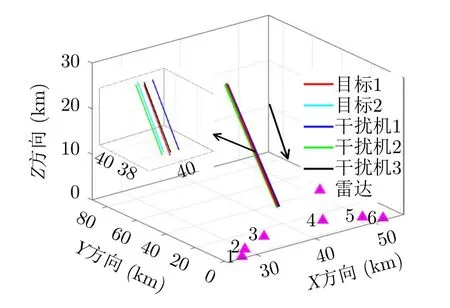
图4 多目标突防组网雷达Fig.4 The scenario of multiple targets penetrating the NRS

图5和图6分别是优化算法和稳健算法的资源分配结果，图中不同的颜色代表不同的功率值。为了方便比较，将功率分配结果进行归一化处理。

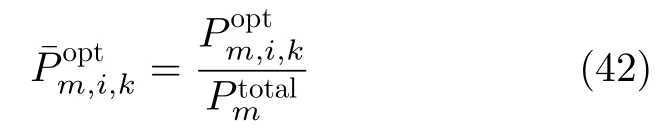
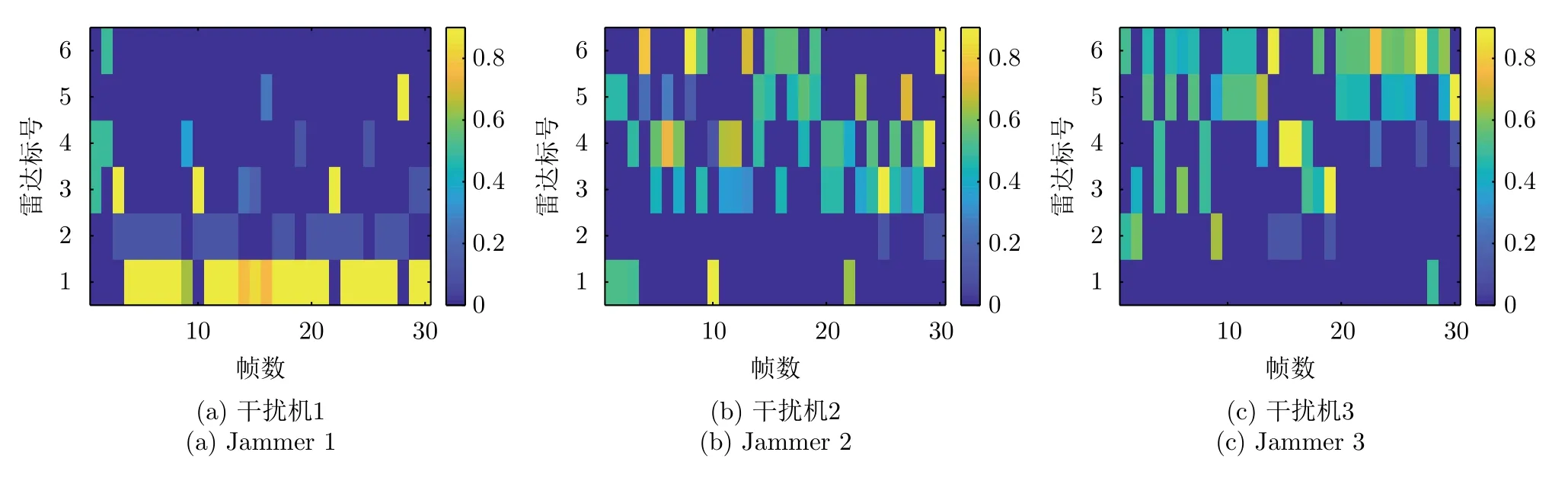
图6 稳健算法资源分配结果Fig.6 The results of resource allocation achieved by the proposed robust strategy

图7给出了3种资源配置方式下组网雷达对两个突防目标的检测概率。两个目标的检测概率基本一致是因为两个目标距离较近，相对于各雷达节点的空间位置差异性不明显。从图7(a)和图7(b)看出，相比传统资源配置方式，干扰资源经优化分配和稳健优化分配后两个目标的检测概率明显降低，这证明了本文所提两种方法均能有效压制组网雷达，提升整个干扰系统的性能。只考虑距离不确定性时，相比优化算法，通过稳健算法得到的两个目标检测概率较大，说明了距离不确定性会影响干扰效果。

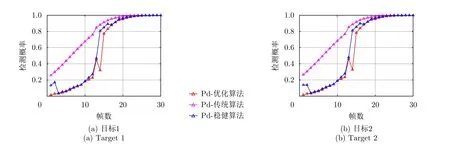
图7 突防目标检测概率Fig.7 The detection probability of penetrating targets

图8是优化算法与传统算法、稳健算法的全局代价函数值对比图。由图8可见，本文所提优化算法和稳健算法的全局代价函数值更小，进一步验证了本文所提方法的有效性。

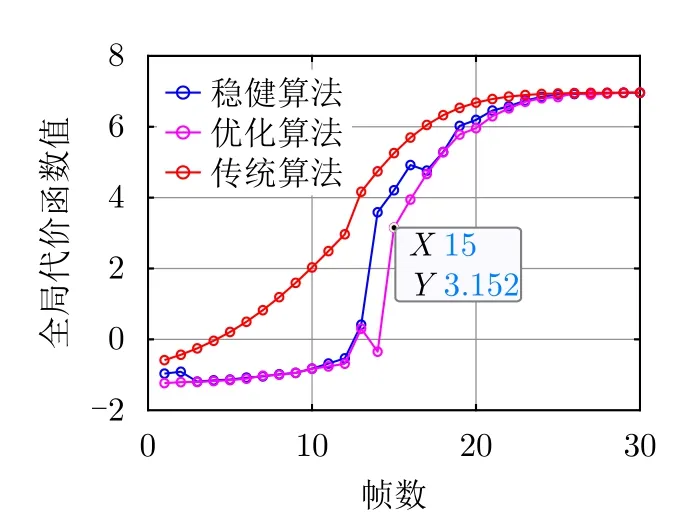
图8 全局代价函数值Fig.8 The value of global cost function

图9是用PSO求解优化问题式(33)时代价函数适应度值随迭代次数变化的曲线。由图9可见，随迭代次数增大，代价函数适应度值逐渐收敛，说明了PSO求解方法是可行的。

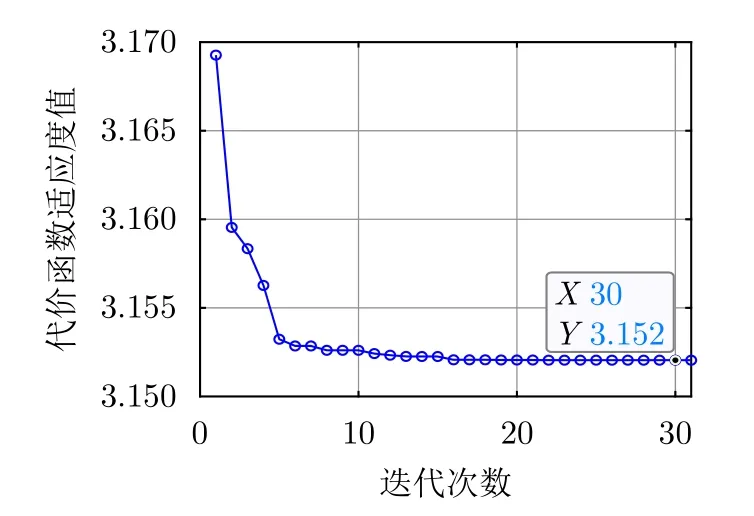
图9 k=15时代价函数适应度值收敛曲线Fig.9 The convergence curve of the cost function fitness value atk=15

6 结束语

本文针对多目标突防组网雷达的场景，提出了一种面向组网雷达干扰任务的多干扰机资源联合优化分配方法，在干扰资源有限的条件下，通过优化分配各干扰机的波束和功率资源，最小化组网雷达系统对突防目标的检测概率。之后，采用PSO分两步对上述优化问题进行求解。仿真结果表明，与传统方法相比，本文所提优化方法在干扰资源有限的条件下，通过优化配置干扰资源更能有效降低组网雷达对突防目标的检测概率，提升了多干扰机对组网雷达的协同压制干扰性能。需要指出的是，优化算法中的检测概率是在已知敌方组网雷达位置、融合方式以及融合准则等参数信息的理想情况下计算得到的。但在实际对抗环境中，考虑到获取组网雷达参数难度大和参数估计精度有限带来的检测概率泛化误差，本文建立了基于组网雷达参数不确定性的干扰资源稳健优化分配模型。仿真结果表明，相比传统方法，本文所提稳健方法提升了多干扰机对组网雷达的协同干扰性能，且有较好的鲁棒性。