增阻离轨装置气动特性的DSMC研究

王立武,冯瑞,张九双,王广兴,王奇,何青松

(1.东南大学国家预应力工程技术研究中心,南京 211189;2.北京空间机电研究所,北京 100094;3.中国航天科技集团有限公司航天进入、减速与着陆技术实验室,北京 100094)

1 引言

随着人类太空探索活动的日益频繁,发射任务过程中产生的大量火箭抛弃物和废弃航天器滞留在太空中[1]。其中,近地轨道 (LEO)区域尤为严重,容纳了约90%的空间碎片,对当前和未来的航天器在轨运行造成了巨大的安全隐患[2]。控制空间碎片数量已经成为业界共识,并成为世界主要航天国家的优先事项之一。目前,最有效的方法是将寿命末期的航天器从轨道上及时移除[3,4],主要的离轨方式包括推力离轨、太阳帆离轨、电动力绳离轨以及增阻离轨等。其中,增阻离轨技术以大收拢比、质量轻、成本低、不需额外燃料等优势,在LEO空间碎片减缓方面具有广阔的应用前景。其原理是通过展开大面积的增阻面来有效提升寿命末期航天器的面质比,同时减小弹道系数,充分利用稀薄大气阻力对航天器进行快速降轨并最终进入稠密大气层烧毁[5-8]。因此,准确预测所选增阻离轨装置稀薄流区的气动特性对总体设计具有重要意义。

在稀薄流域,分子之间间距较大,经典连续介质假设不再成立,广泛用于飞行器流场数值模拟的NS方程、Euler方程等不再适用。故需要从微观分子模型角度出发,采用稀薄气体动力学方法开展研究。在求解稀薄气体动力学问题的诸多方法中,DSMC方法被认为是20世纪下半叶稀薄气体动力学的代表性成果,是当前工程实践中求解稀薄流域问题的主流方法。

DSMC方法由G.A.Bird于1963年提出,并首次应用于气体分子的内能松弛问题[9]。而后用于二维、三维流动数值模拟,并且成功应用于多个型号飞行器的气动特性计算。所得结果与实际飞行测量得到的数据相符度较高,如美国航天飞机升阻比的预估。后来众多学者不断从网格技术、分子碰撞模型、计算效率等方面对该方法予以发展完善,并多次用于工程实践中三维复杂外形流场模拟,比如AFE飞船、三角翼、“哥伦比亚”号航天飞机事故分析、火星探测器减速装置Ballute气动加热分析。国内沈青、樊菁等最早针对DSMC方法也开展了相关研究[10-12]。

本文首先详细介绍了DSMC数值模拟方法的相关理论,然后对DSMC方法进行了标模验证;最后将DSMC方法应用于増阻离轨装置稀薄流场下的气动特性预测。

2 DSMC数值模拟方法

DSMC方法是基于气体动力学理论发展而来的数值仿真方法,DSMC方法被严格证明是与玻尔兹曼方程等价的[11]。DSMC方法基本原理是在计算机中用大量模拟分子代表真实气体,模拟分子的空间坐标、速度、内能等存储在计算机中,因分子运动、碰撞以及与边界的相互作用而随时间变化。该方法的核心思想是在一个时间步长内,将分子运动与碰撞解耦,所有分子首先按照各自的速度,运动一段距离,然后再按照与真实分子相同的碰撞频率,根据一定的碰撞模型,从所有可能组合的分子对中选出碰撞对,以几率的方式分配碰撞后的分子速度和内能、决定是否有化学反应发生等。

下面主要对DSMC中分子与物面相互作用模型、分子碰撞模型以及碰撞对选取等进行介绍。

2.1 分子与物面相互作用模型

稀薄流气体分子与物面相互作用过程的模拟,直接影响DSMC方法对气动力、热的计算精度。本文采用镜面反射和漫反射两种相互作用模型。其中镜面反射假设气体分子与物面发生弹性碰撞;漫反射模型假设气体分子与物面发生非弹性碰撞,且反射后的气体分子向各个方向散射,散射后的分子速度满足平衡的Maxwell分布,该分布只与反射后分子温度有关,与入射分子的动量速度无关。入射分子的动量取决于自由来流的条件,反射分子的动量特性用动量协调系数来刻画,不同的协调系数取值则代表了不同的碰撞模型。法向动量协调系数σN表示分子与面碰撞过程中法向动量的改变,切向动量协调系数σT则表示分子与面碰撞过程中切向动量的改变,计算公式如下:

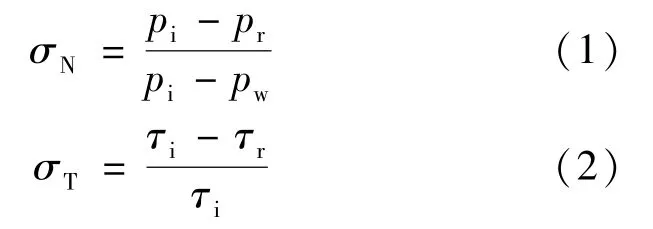
式中,pi、 τi和pr、 τr分别为入射分子与反射分子的法向压力和切向压力;pw为壁面法向压力。由此可知,发生镜面反射碰撞时有σN=σT=0,发生漫反射碰撞时则有σN=σT=1。

2.2 分子碰撞模型

稀薄流场条件下的气体分子满足三体碰撞不重要条件d3/δ3≪1,即分子之间发生三体或者以上碰撞的概率要远小于双体碰撞。因此在考虑分子碰撞模型时,仅考虑双体碰撞。此时,利用动量守恒和能量守恒定律可以得到:

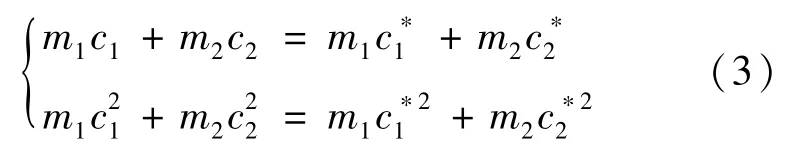
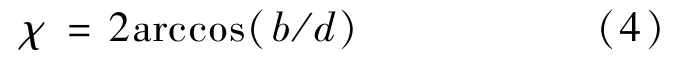
式中,b是分子间距;d是分子直径。得到偏转角以后,结合公式 (3),可求得碰撞后的分子速度,且速度方向在各个方向均匀散布。

2.3 分子碰撞对选取

分子碰撞对的选取常有的有两种方法:时间计数器 (Time Counter,TC)法、无时间计数器 (No Time Counter,NTC)法。本文中的分子碰撞对选取采用常用的无时间计数器 (No Time Counter,NTC)法[13]。用假设的单个模拟分子来代替的一定数量的真实分子,则计算碰撞对发生概率P时,仅需考虑所有碰撞对的一部分并同时将P按相同的倍数加以放大。倘若该倍数可使得最大碰撞概率为1,则可以理解为计算效率最高。可以得到,需要做计算处理的碰撞概率P的表达式为:

式中,σT是分子碰撞截面;cr是两个分子的相对速度。

2.4 仿真程序简介

本文采用由Sandia实验室开发的稀薄流计算开源代码SPARTA进行分析计算。SPARTA基于DSMC算法,采用笛卡尔网格对粒子进行跟踪和分组;其包含多种粒子碰撞模型,化学反应模型以及壁面边界条件模型。近年来已经在很多工程实践和学术研究中得到了充分的验证和应用。

DSMC方法在SPARTA程序中实现流场如图1所示。SPARTA程序采用的是笛卡尔网格,程序开始后需要初始化网格信息,包括粒子数目、网格节点数目及边界条件等;然后计算粒子在Δt时间步内的运动及粒子与物面的相互作用;更新粒子索引信息,将分子重新排序和编号;按照规定碰撞模型进行粒子间碰撞计算;流场取样;判断是否达到计算时间;最后计算平均流场信息:非定常流场对各个重复过程进行系综平均,定常流动在定常化后求足够大时间的时间平均。

图1 DSMC实现流程框图Fig.1 Flow chart of DSMC implementation

3 SPARTA程序标模验证

NASA基于DSMC开发出一套行业标准软件工具DAC(DSMC Analysis Code),该软件对于航天器在自由分子流区的气动分析具有很高的计算精度。

本文采用SPARTA程序对球算例进行了自由分子流域内的气动性能进行了模拟仿真,并与DAC软件结果进行了对比。

数值模拟工况如表1所示。

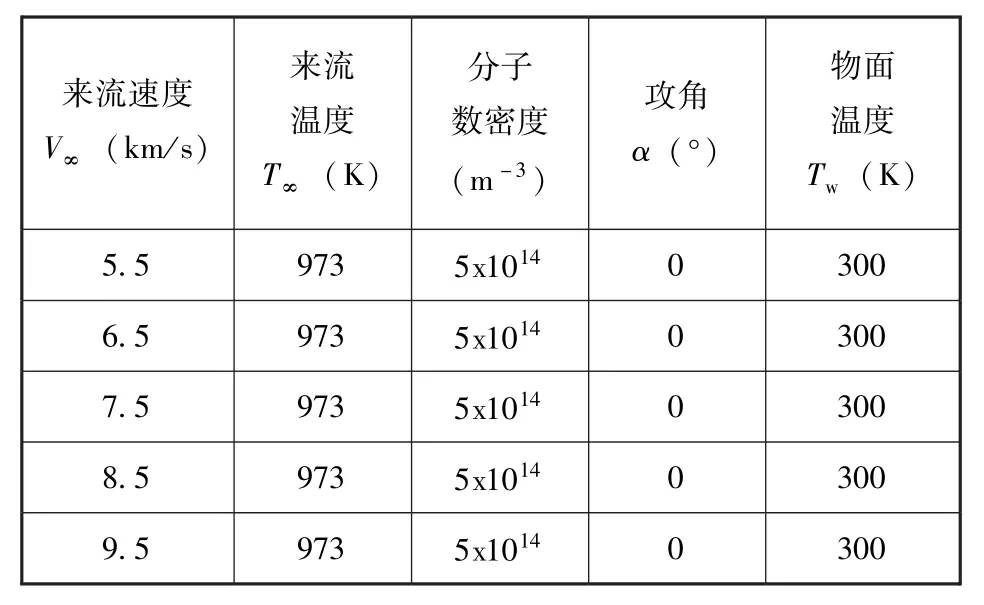
表1 球算例计算工况Table 1 Calculation conditions for ball calculation examples

图2分别给出了球面时均压力与对称面时均速度云图。从图中可以看出在球的迎风面存在一个高压区,压力量级约10-5,在背风区由于来流粒子与球面动量交换较少,因此压力明显较低。

图2 球表面时均压力云图 (a)与对称面时均速度云图 (b)Fig.2 Hourly average pressure on the surface of the ball(a)and time-averaged velocity distribution cloud diagram of symmetry plane(b)

从图2中可以看出,粒子速度在远场为来流速,随着粒子靠近球面,粒子与球面发生碰撞完成动量交换后,粒子速度明显降低;粒子经过球面,在球面背风区粒子数目相对较少,接近真空环境。

图3给出了SPARTA和DAC软件不同工况阻力系数对比曲线。不同工况下由文中计算得出的阻力系数与DAC计算得出结果吻合程度很好,其中镜面反射碰撞模型的最大计算误差仅为0.53%。由此可知文中采用的计算方法和程序可对自由分子流区航天器增阻面的阻力系数给出可靠的计算结果。

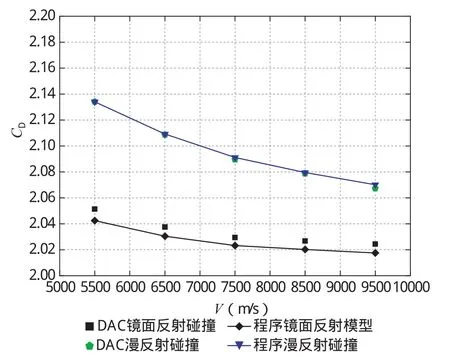
图3 SPARTA与DAC软件球阻力系数对比Fig.3 Comparison of ball drag coefficient between SPARTA and DAC software

4 增阻离轨装置稀薄流气动特性预测

增阻离轨空间碎片清除技术是一项适用于近地轨道区域任务后航天器离轨的新技术,对于轨道高度小于850km的任务后航天器,通过增阻离轨系统形成很大迎风面,增加大气阻力,从而逐渐降低并脱离运行轨道,在一定时间内陨落,再入大气层烧毁。该技术可用于废弃卫星、微小卫星、废弃的运载火箭上面级的离轨,应用前景广阔。

本文将SPARTA程序应用于增阻离轨装置在稀薄流域内的气动特性数值预测。仿真工况如下:

表2 计算工况Table 2 Calculation conditions

图4给出了物面压力和对称面速度云图分布,与球算例类似,迎风面存在高压区;物面附近速度降低,物面后存在近似完全真空区域。

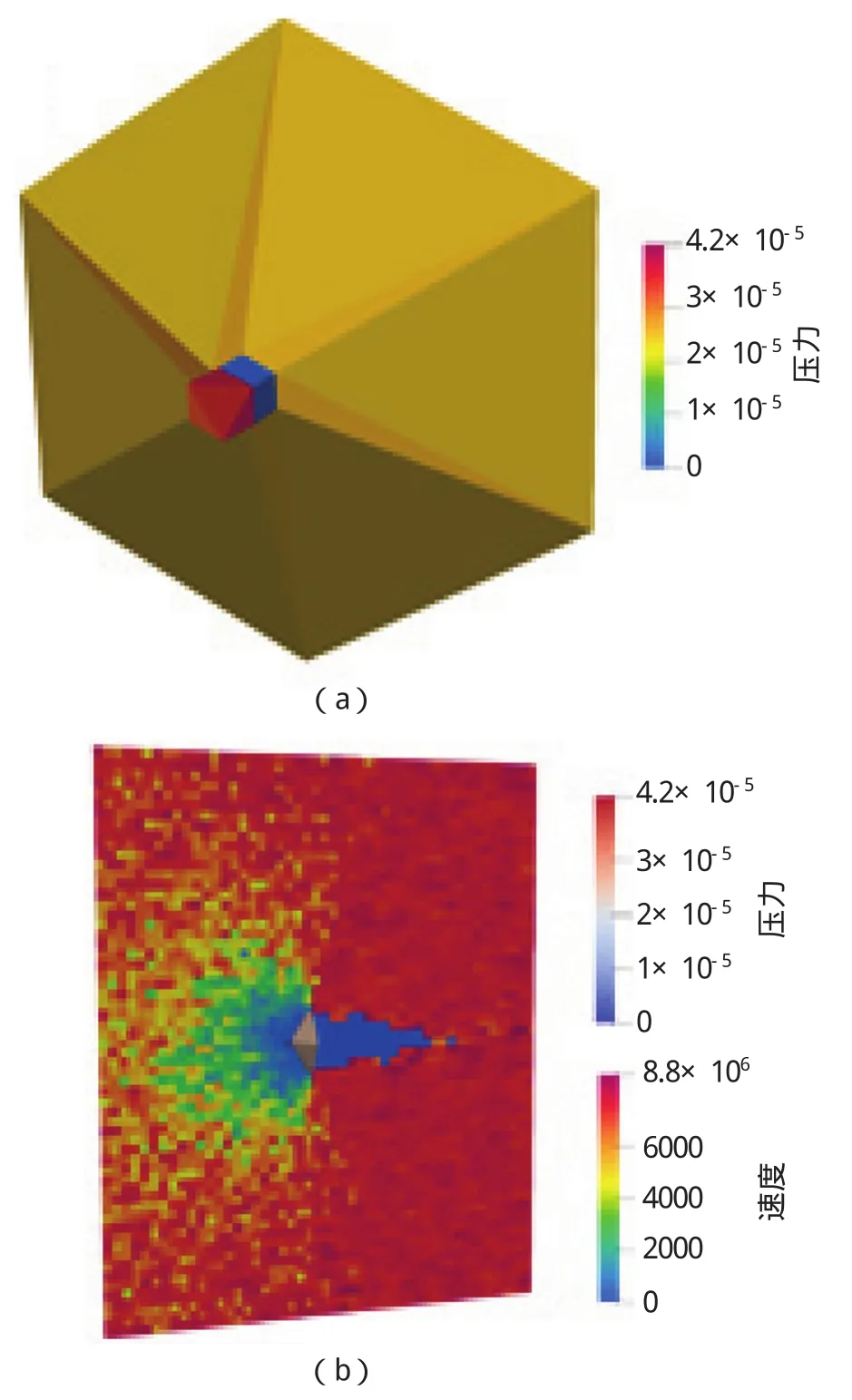
图4 增阻离轨装置物面时均压力云图 (a)与对称面时均速度云图 (b)Fig.4 Time-averaged pressure cloud diagram of the object surface of the drag-increasing de-orbit device(a)and time-averaged velocity cloud diagram of symmetry plane(b)

图5为增阻离轨装置在不同攻角下阻力系数曲线,由图中可以看出攻角的变化对漫反射碰撞模型的气动阻力系数影响较大,且阻力系数随攻角增大有显著减小的变化趋势;当攻角在0°～30°之间变化时,攻角变化对镜面反射碰撞模型的气动系数的影响很小,而当攻角在30°～90°之间变化时,气动阻力系数对攻角的变化较为敏感,会随攻角的增大有显著快速衰减的变化趋势。

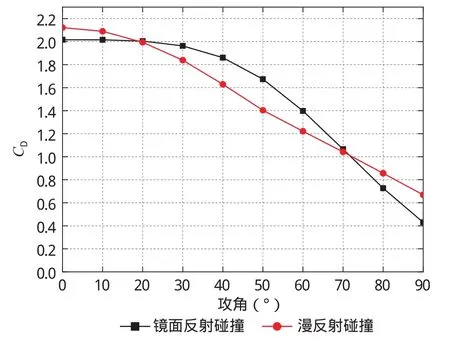
图5 增阻离轨装置在不同攻角下阻力系数曲线图Fig.5 The drag efficient curve of the drag-enhancing de-orbit device at different angles of attack

不同轨高处的稀薄大气在分子的种类、数密度及来流温度等方面存在一定差异,表3给出了7.5km/s、1000K来流温度、0°攻角条件下,不同轨高处气动阻力系数计算结果。

表3 不同轨道阻力系数Table 3 Drag coefficient of different tracks

结果表明,阻力系数随轨道高度的变化不明显,但由于不同轨道高度处大气密度差距较大,不同轨高处的气动阻力差距也较大。

5 结论

本文首先通过SPARTA程序对球标模进行了模拟并与DAC软件结果进行了对比,两者误差较小;然后将SPARTA程序应用于增阻离轨装置在不同攻角工况气动特性仿真,结果表明在0°～30°攻角下,增阻离轨装置随着攻角增加阻力系数下降较缓,而当攻角在30°～90°时,阻力系数下降明显,轨道高度对气动阻力系数的影响较小。