采用双核模型研究超重核合成机制
2021-09-01王艺澎郭树青包小军邓军刚张鸿飞
王艺澎,郭树青,包小军,邓军刚,张鸿飞
1.兰州大学核科学与技术学院,兰州 730000
2.深圳大学光电工程学院,深圳 518061
3.湖南师范大学物理与电子科学学院,长沙 410081
目 录
I.引言 157
II.低能重离子核反应 158
A.深度非弹性碰撞 159
B.熔合反应 159
III.双核模型 159
A.双核模型的两种解释 159
B.理论框架 160
1.俘获截面 160
2.熔合几率 160
3.存活几率 161
C.主方程发展 161
1.一维主方程 162
2.二维主方程 163
3.三维主方程 164
IV.总结与展望 166
参考文献 166
I.引言
原子核系统中主要存在三种相互作用:质子间的库仑相互作用、核子间的强相互作用、β衰变过程中的弱相互作用。一般重核或超重核系统很不稳定,存在着复杂的相互作用,系统可以自发地通过α衰变、自发裂变等衰变类型向能量较稳定的状态演变。根据液滴模型,库仑力与核力的竞争使得原子核在拉伸形变过程中存在一个势垒,阻挡原子核发生裂变。对很多Z=98[1]以后的核素,由于核力近似与核子数成正比,库仑力与Z2成正比,导致裂变位垒随质子数的增加而降低,自发裂变几率的分支比大于α衰变分支比。当Z=104左右时,裂变位垒趋近零,自发裂变寿命小于10−14s,按照经典液滴模型理论预言,不存在104号以上的元素[2]。
1949年,Mayer等提出原子核的壳模型[3],成功地解释了幻数的存在。对于双幻核附近的原子核,壳结构效应足够的强使其形状近似为球形,显著增加了原子核的裂变位垒,延缓其自发裂变,为探索更重的核提供了可能。自1965年以来,以Myers[4]、Nilsson[5]为代表的理论物理学家,预言了以Z=114,N=184为中心的一片寿命较长、相对稳定的原子核,即超重核稳定岛[6]。此后,又有Skyme-Hartee-Fock[7]、相对论平均场[8]等不同模型对之进行了验证。与此同时,世界各核物理实验室,比如俄罗斯超重核工厂Dubna[9]、德国重离子中心GSI[10]等都积极开展了新一轮超重元素的合成研究[11,12]。
目前,超重核合成领域取得了一些成就。2016年,国际纯粹与应用化学联合会(International Union of Pure and Applied Chemistry)和国际纯粹与应用物理学联合会(International Union of Pure and Applied Physics)联名确认了所有已合成的元素并予以命名[13,14]。(表1:超重核元素首次合成的相关信息[15–27]),但在实验上对Z>118的超重元素截面仅仅给出fb量级[11]。

表I.超重核元素首次合成的相关信息
理论上,一方面区别于轻体系的熔合反应,重离子完全熔合过程中存在复杂的动力学形变;另一方面完全熔合过程不提供任何信息来描述复合核的形成过程。基于此,理论物理学家发展了各种模型来描述完全熔合过程。Swiatecki等人发展了宏观动力学模型[28,29],将原子核认为是有粘滞性的液滴,熔合过程是纯粹的动力学过程,但该模型忽略了原子核的壳效应及反应过程中的统计性质。Aritomo等人在宏观动力学的基础之上,考虑壳修正及统计涨落效应发展了涨落–耗散模型[30–32],该模型适用于计算蒸发剩余截面、(准)裂变产物的质量分布,但对质量较对称的弹靶组合,给出过大的蒸发剩余截面。Zagrebaev等人发展了核子集体化模型[33,34]:弹核、靶核接触后,一些核子逐渐从两核逸出,被两个原子核共有。随着共有核子的增多,弹核、靶核的区别逐渐消失,但该模型的物理图像目前仍存在较大的争议。Adamian等人发展了双核模型[35],假定碰撞动能充分耗散后,双核系统由轻核转移核子到重核形成复合核,通过实验数据对比得出,该模型适用于描述超重核的生成截面。尽管不同模型在不同方面描述了超重核的形成过程,但是由于理论计算中存在许多不确定因素,不同模型给出的熔合几率相差几个数量级,因此给出可靠的生成截面和入射道参数还比较困难[36–38]。
在描述熔合过程的诸多模型中,双核模型是影响最大的一个[36]。Adamian等人对势能面进行近似处理[35]大大削弱了原子核的结构效应。中科院近物所李君清研究员等人发展了双核模型[39],用数值求解主方程“精确”描述核子转移过程,不对势能面做近似处理。本文在双核模型的理论框架内,采用李君清等人的处理方法,着重探讨双核模型主方程的发展过程,深度诠释了双核系统的熔合过程,为新核素的合成提供了理论依据。
II.低能重离子核反应
在核反应问题中,入射粒子与靶核所组成的体系处在非束缚态。核反应研究的是体系碰撞前后不同状态的跃迁几率或反应截面。
推广壳模型观点,可以考虑入射粒子在靶核的平均势场作用下运动,但入射粒子与靶核间的作用可使靶核激发。如果只激发了靶核内的个别自由度,则反应机制比较简单,称为直接反应。入射粒子与靶核作用损失能量足够多时,与靶核一起形成了一个复合系统,该复合系统的激发能还将逐渐分布到越来越多的自由度,形成极端复杂的复合核状态。这样的反应可基本上分为复合核的形成与随后的衰变两个阶段,称为复合核反应。
从轻离子核反应扩展到重离子核反应是核反应的一个重要发展[40]。重离子核反应是指比α粒子更重的粒子所引起的核反应[41]。其中,对深度非弹性碰撞和全熔合反应的研究,可以揭示出能量、角动量、质量、电荷在原子核小体系中的输运过程[42],为合成超重核提供条件。
A.深度非弹性碰撞
深度非弹性碰撞是重离子核反应所特有的一种反应机制。在深度非弹性碰撞中,入射粒子能量Ec.m>库仑势垒Vcb,要使弹核深入到靶核表层,碰撞参数b应满足下述关系:

式中bg指擦边碰撞参数,bcr指发生熔合反应的临界值。
深度非弹性碰撞过程大体可分为三个阶段。第一阶段称为接近相。在接近相,两个粒子A、B以适当的碰撞参数b作相对运动,在光学势的作用下,彼此接近。第二阶段为碰撞的主要阶段,又称耗散相。在耗散相,A、B的最大密度半径相互接触,全部径向耗散殆尽,开始粒子交换,相对运动的角动量开始转化为两个核的转动角动量,同时两核做相对运动。第三阶段称为终了阶段,分为分离相和熔合相。在分离相,两个核由于库仑斥力分开,输运过程终止;在熔合相,由于核力的强相互作用,两个核熔合在一起,输运过程向统计平衡发展[40]。
深度非弹性反应机制的研究能够揭示重离子核反应过程的动力学效应,特别适合研究多个自由度的弛豫现象,并由此获得非平衡核态过渡到平衡核态的详细信息[41]。实验结果表明:入射粒子和靶核的特性基本可以保持,大量的相对运动动能被耗散和相当大的一部分轨道角动量转化为两核内禀角动量[40]。其中,重离子深度非弹性碰撞中的输运过程可以用Fokker-Planck方程[43]研究。
B.熔合反应
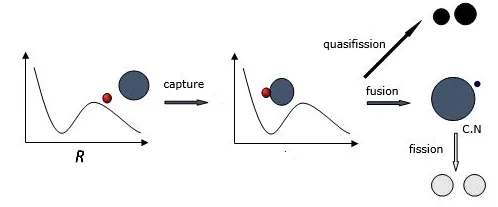
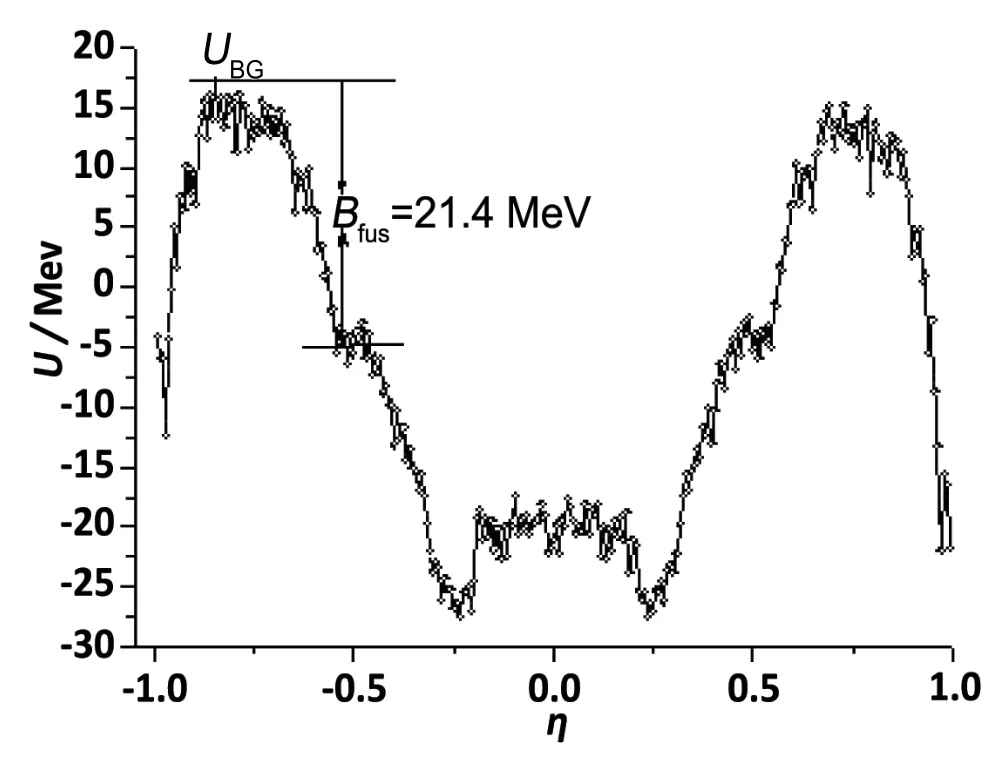
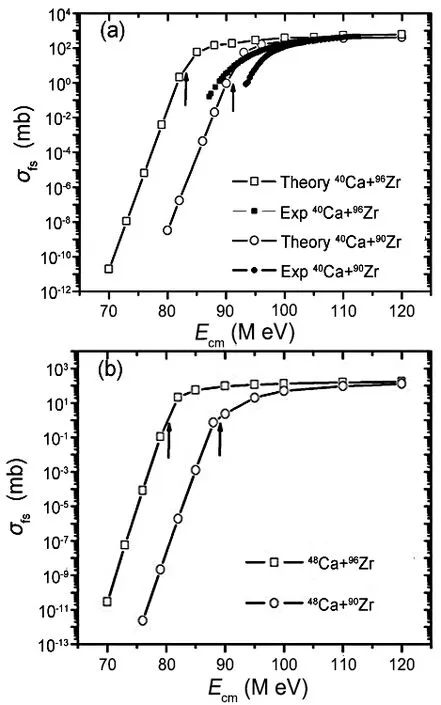
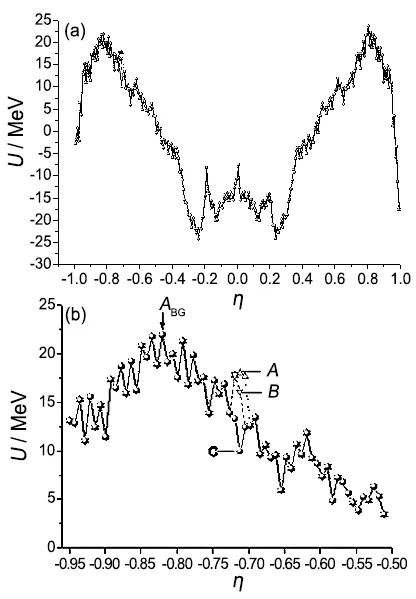
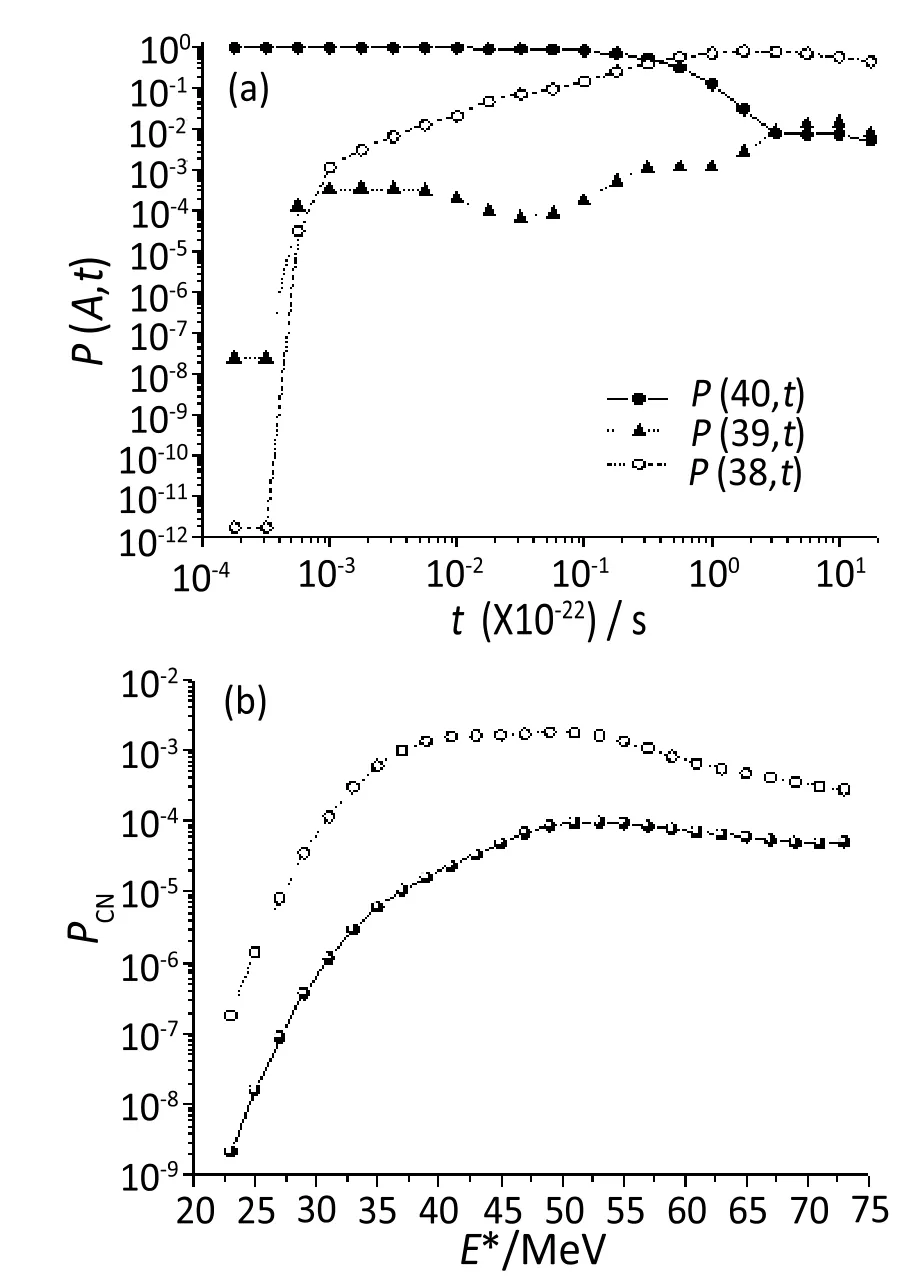
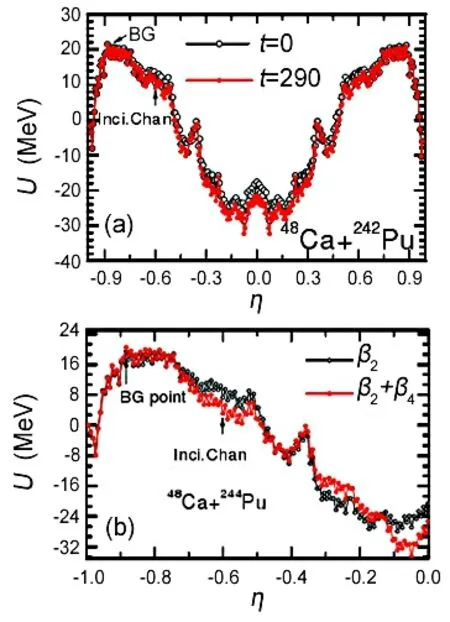
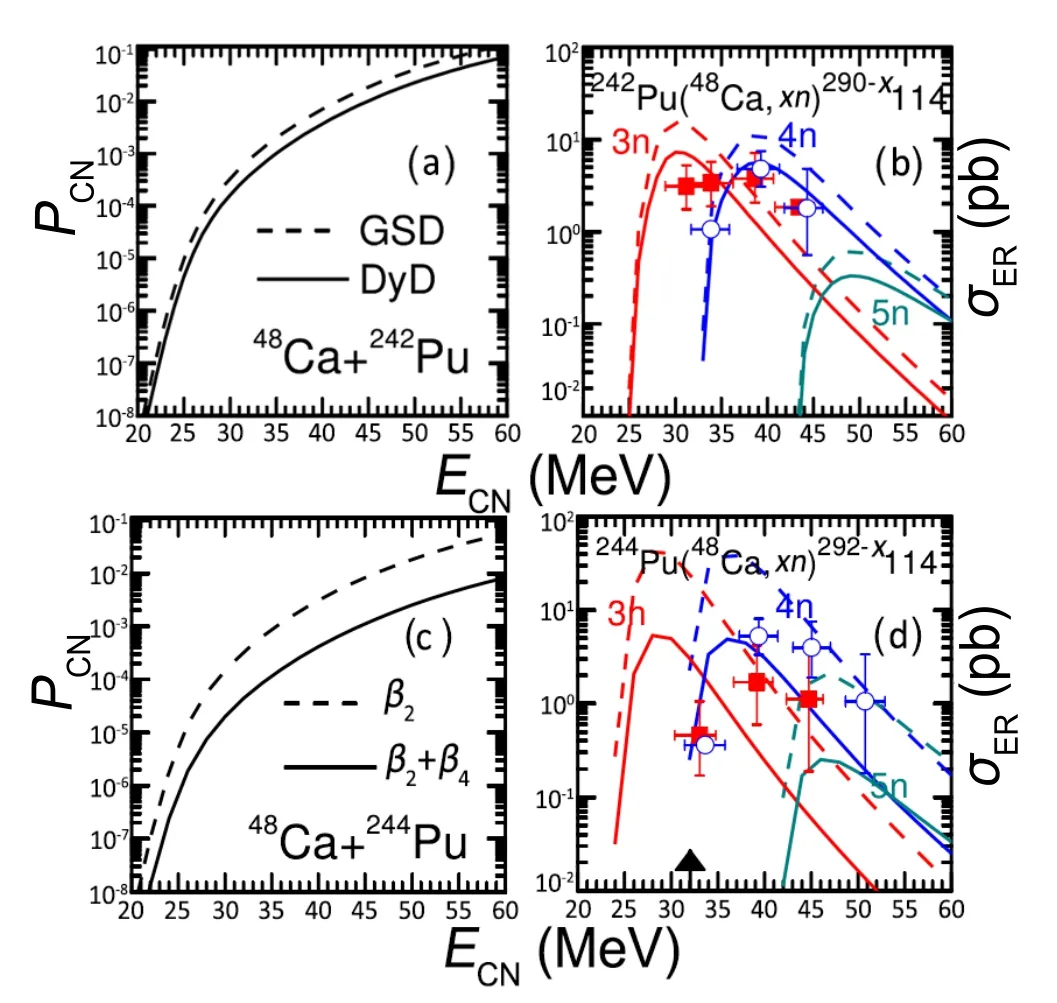
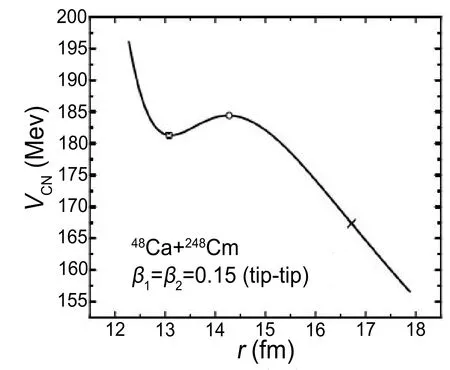
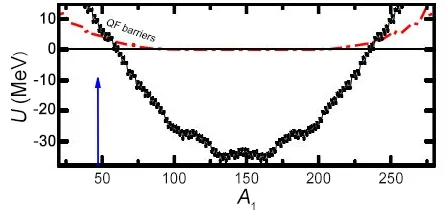
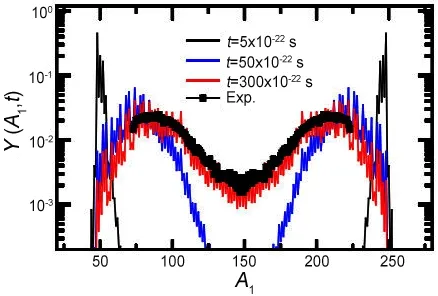
对比深度非弹性碰撞反应的适用条件,当碰撞参数b 根据熔合反应的静态理论,系统要超越静熔合势垒才能发生熔合,但由于摩擦,到达熔合势垒前,一部分相对运动动能已经转化为内禀激发能,需要有额外动能E来补偿摩擦引起的动能耗损。而对于非中心碰撞情况,切向摩擦引起相对角动量的耗损,系统的作用势需要进行修正。实验结果表明,熔合过程主要由碰撞早期行为决定[40]。 在熔合反应的动态解释中,基于经典模型,作用势必须有一个“窝”,而且达到复合核状态的弛豫时间应小于体系逗留在“窝”内的时间。当能量略高于库仑势垒时,对某一特定的角动量l,主要问题在于能否进入熔合势垒V lf。这里lf是到达势垒时留有的角动量。对涉及较大的l值,由于作用势“窝”的限制,熔合截面呈1/Ec.m下降[40]。 重离子熔合反应(包含新的反应机制)基于新的实验结果,探讨垒下熔合,额外推动模型,快裂变等熔合过程中的动力学问题[40]。目前,主要采用唯象的耗散过程的观点[33,35,44]解释重离子核反应的各个方面。 目前,合成超重核最主要的途径是重离子熔合蒸发反应[45]。实验室通过低能重离子核反应合成超重核,即P+T→C→B+n,p,α,γ[41]。首先,用加速到一定能量的重离子束流轰击靶核产生复合核。其次,复合核通过蒸发粒子退激能量,但发射粒子不能带走很多角动量,剩余核通过级联跃迁退激到基态,具有非常高的自旋态。最后,在反冲余核的飞行过程中利用电、磁等相关技术进行分离,分离后的余核被具有单原子衰变测量能力的探测系统进行测量与鉴别[46]。 研究重离子核反应的基本任务是弄清反应机制,判断发生这类反应的条件,提出理论模型,定量的计算反应的各种物理量[40]。用双核模型研究超重核的合成机制,最主要的部分是由双核系统演化到复合核的熔合机制[35,47,48]。 双核模型的思想是,在深度非弹性碰撞过程中,入射而来的弹核被靶核俘获形成双核系统。伴随着相对运动能量的耗散,在相互作用时间内两核之间发生大量的核子转移、能量及角动量的耗散与弛豫,不断形成新的双核系统,即弹、靶核仍保持其各自的独立特征[35]。 对完全熔合反应,双核系统认为它和深度非弹性碰撞的核子转移反应具有相同的反应过程[35],只不过是弹(靶)核中的所有的核子全部转移到靶(弹)核中,最后形成复合核。在一系列核子转移的过程中,复合核沿着质量不对称度增大的方向不断演化。这样,双核模型不仅可以很自然地解释形成复合核时存在内部熔合位垒,还解释了双核系统向复合核演化过程中熔合与准裂变的竞争机制。 值得说明的是,围绕势能面的计算与核子转移过程,双核模型有两种解释。Adamian[35]等假定在碰撞动能充分耗散之后,双核系统由轻核到重核转移核子而形成复合核,复合核包含了全熔合与准裂变的竞争两个过程。此时计算超重核截面包含了结构效应,但该模型用Fokker-Planck描述核子转移过程,用了Gaussian类型的解而对势能面采用了谐振子近似,或者Kramers类型的准静态近似及谐振子近似解。而事实上奇偶修正的势能面与谐振子势相差甚远,原因在于双核系统势能面包含了反应系统的结构效应,谐振子近似削弱了此效应。 中科院近物所李君清研究员[39]等人在双核模型框架内,通过数值求解描述熔合过程的主方程,得到熔合几率随激发能的变化行为,并且在这个过程中不对驱动势做谐振子近似。计算过程考虑了核子转移与相对运动中能量、角动量、碎片形变弛豫过程相耦合,用微观方法推导与相对运动的能量耗散有关的核子跃迁几率,因而与时间相关。该计算结果保留了更多的动力学效应,并在计算熔合几率考虑了弹核与靶核的形变及相对取向对反应的影响等。对以Pb为靶及以48Ca为炮弹的反应,计算了一系列生成超重核的蒸发剩余截面,所得结果与实验数据在数量级上很好符合[49]。 根据N.Bhor的复合核的形成和衰变过程相互独立的假设与V.F.Weisskopf提出的核合成反应的三阶段模型,理论上通常将超重核合成动力学过程分为俘获阶段、熔合阶段或复合核形成阶段,以及复合核的退激发阶段[35]。 在俘获阶段,弹核需要克服与靶核之间的库仑位垒,被靶核俘获形成双核系统。当两核处于熔合阶段时,双核系统向复合核方向演化,在这个过程中时刻都有准裂变发生,但仍有几率克服“内部位垒”,形成超重复合核。在退激发阶段,复合核一般具有较高的激发能,具有很大的裂变几率,但也有一定几率通过蒸发一个或多个中子或轻带电粒子来退激发,超重核最终得以“存活”下来[36],如图1所示。 图1.双核系统概念的物理图像 于是,目标超重核的生成截面可以表示为不同分波下三个因子乘积的求和,表示为[50]: 式中Ec.m为质心系下入射能,J为角动量,σc(Ec.m,J)为俘获截面,PCN(Ec.m,J)为熔合几率,Wsur(Ec.m,J)为存活几率。 1.俘获截面 两核从无穷远处相互靠近时,包含库仑力与核力的相互作用,在以双核质心距离R为函数的有效势能曲线上会形成一个口袋和库仑位垒。穿透几率受库仑位垒高度及口袋宽度的影响。俘获分波截面[34]可以表示为: 式中,µ是折合质量,T(Ec.m,J)是穿透几率。 式中ω(J)是RB(J)处库仑位垒位置对应的曲率刚度,需在计算中考虑其位垒分布函数。 2.熔合几率 两核之间发生核子转移时,一个核的核子全部转移给另一个核时形成复合核,这个过程可以用主方程描述。弹、靶核在克服库仑位垒相接触后,双核系统将沿着两个自由度变化。一是沿两核之间距离R的变化,二是两核交换核子过程中,双核系统沿质量不对称度η的变化。 在碰撞过程中弹、靶核相接触时,有核子、能量、角动量等在两核间进行转移、交换。设反应中始终保持两体过程,碎片1、2的质量数分别是A1、A2,总质量数A=A1+A2。在t时刻,碎片1的激发能为E1时的分布几率为P(A1,E1,t),考虑两核交换核子过程中的准裂变与重核裂变,主方程为[39]: 图2.反应道64Ni+208Pb的驱动势,B fus是内部熔合位垒[49] 式中W表示碎片1的质量数为A1,内部激发能为E1时向(A′1,E′1)态跃迁的几率。dA1表示碎片在(A1,E1)宏观状态时所包含的微观状态的维度,并对碎片1所能取的所有状态进行求和。(Θ)是沿两核距离R的准裂变速率,(Θ)为裂变速率。系统驱动势[34]为: 式中,Atot=A1+A2。A1、A2是双核系统中类弹和类靶核的质量数。ULD(A1)、ULD(A2)和ULD(Atot)分别为对应的碎片1、碎片2和复合核的结合能,包括了壳修正和奇偶效应。 式中UC和UN分别为两核的库仑相互作用能和核相互作用能,V′rot为复合核转动能。UC由式(9)给出,UN采用与动量和自旋无关的Skyrme类型的核子–核子相互作用双折叠势。 (64Ni+208Pb→272Ds*) 反应系统的驱动势在图2中给出,箭头所标的位置是入射道位置。对确定的角动量分波J,所有能越过势能面最高点UBG的分布几率都将最终达到复合核。所以熔合几率用下式表示: 式中τint是相互作用时间。 3.存活几率 重离子熔合形成的复合核需要通过发射中子、带电粒子等方式退激发。对于重核,发射带电粒子需要克服库仑位垒才可以从原子核中分离出来,此时库仑位垒比裂变位垒和中子分离能要高许多,而且只有当激发能低于中子分离能时,发射带电粒子作用才比较明显。因此,目前考虑复合核退激发的存活几率只考虑了中子蒸发与裂变的竞争。这样,自旋为J、激发能为E*的超重复合核通过蒸发x个中子而存活下来的几率表示为[49]: 式中Γn(E*i,J)为第i个中子的蒸发宽度,Γf(E*i,J)为蒸发第i个中子前的裂变宽度,E*i为蒸发第i个中子前的激发能。P(E*)描述退激发状态,由Jackson简化的中子蒸发公式给出。 重离子熔合反应是一个复杂的多自由度的输运过程,多自由度(η,β1,β2,R,θ)及多反应道(熔合、准裂变、重核裂变)的耦合使得动力学演变十分复杂。在此过程中,宏观集体自由度的选择关系到系统状态能否被合理描述。原则上宏观自由度越多,系统状态越能得到精确描述。 实验上观察到的深度非弹性碰撞中的弛豫现象[41],曾借助Fokker-Planck方程[35]、主方程[39]以及更普遍的输运方程描述。对核的内部状态演化采用非定态、能反映弛豫过程的主方程描述,如此不仅能给出物理量的平均值,还能给出其涨落、分布情况。除了方程描述的差异性外,双核模型也经历了自由度从一维到三维的演化过程。 1.一维主方程 设在t时刻,碎片1的激发能为E1时的分布几率为P(A1,E1,t),则各组态分布几率由主方程(式6)来描述。此时,描述熔合过程的主方程是一维的,以质量数A1为宏观自由度。与此对应的驱动势也是一维的。 图3.(a)反应道40Ca+90Zr和40Ca+96Zr的熔合截面随入射能的关系,(b)反应道48Ca+90Zr和48Ca+96Zr的熔合截面随入射能的关系[36] 在双核模型中,弹、靶核接近时相对径向动能逐渐耗散到两核的内禀态,使两核均处于激发态。驱动势U实际上是复合系统分为两个相接触碎片的能量,这种复合系统的能量大体在N/Z等于复合系统的中质比处有一个谷。如果相碰撞的两个核不具有这种合适的中质比,则接触后将同时发生质子和中子的扩散,需要调整到合适的中质比[40]。 图4.(a)反应道40Ar+238U→278Ds*驱动势随质量不对称度的关系,(b)图(a)上半部分放大图[49] 内禀激发能引起两核之间的核子转移,转移的核子由较低的势能面或更接近复合系统的中质比来决定。实验发现对弹、靶核的中质比接近于反应道复合系统的中质比时,反应道会给出基本一致的结果[36]。 对于图3(a),两个反应体系的熔合截面随入射能的增加而增加,最后趋于饱和。丰中子靶系统40Ca+96Zr有更高的熔合截面;对于图3(b),质量更非对称的体系48Ca+96Zr有更高的熔合截面,而且系统均在能量较高时这种差别逐渐消失。 重离子熔合需要克服内部熔合位垒,因为高的内部熔合位垒会抑止重离子的熔合。40Ca+90Zr有更高的内部熔合位垒,导致熔合几率随体系变重而下降。但是48Ca+90Zr有更低的内部熔合位垒却给出较低的熔合截面,这是由于熔合几率不仅和内部熔合位垒有关,还和弹靶的质量不对称度有关[36]。 当弹、靶核的中质比远离反应道复合系统的中质比时,中子和质子的转移情况比较复杂,用一维的主方程不能正确描述核子转移,因此不能正确描述熔合过程。这种现象在采用非48Ca弹核轰击锕系靶的反应道中较为常见[49]。 图5.(a)反应道40Ar+238U→278 Ds*分别在A=40、39和38三处的分布几率随时间的演化图,(b)反应道熔合几率随激发能的关系(空心圈:未选择路径,实心圈:选择路径后)[49] 图4是此反应道的驱动势能图。点A=40处是系统入射道,B点与C点分别经过更低势能面。根据经过A点的势能面分别给出A=40、A=39、A=38三处的分布几率随时间的演化图,如图5(a)。在t=10−22s时,A=40处的分布几率已低于10−2量级,势能面分布向A=38处演化,即绝对倾向于沿过C点的最低势能面进行演化。图5(b)描述了不同驱动势对应熔合几率随激发能的关系,从图中可以看出,一维主方程对应驱动势的熔合几率比考虑更低(未经过驱动势路径选择)势能面影响的结果高约2个量级。 由此,入射道在双核系统势能面比较高的位置时,使用一维主方程计算的熔合几率偏差大,进而影响最终蒸发剩余截面的大小。 2.二维主方程 在核结构中,当入射道同位旋与复合系统同位旋相差较大时,单质子能级跃迁不可忽略,它可以使核子壳层与形状出现变化,即壳是同位旋相关的[51]。 一方面,选择单一自由度质量数A,忽略了原子核同位旋效应的影响,另一方面,在核子转移过程中,中子和质子的转移情况比较复杂。结合一维主方程的适用条件,考虑入射道在双核系统势能面较高的位置,对以质量数A为自由度的一维主方程作出修正,建立以类弹碎片中子数N1和质子数Z1为宏观自由度的二维主方程[49]。设反应始终保持两体过程,碎片1、2的中子质子数分别是(N1,Z1)、(N2,Z2)。设在t时刻,碎片1的局域激发能为E1时的分布几率为P(N1,Z1,t),则各组态分布几率由主方程来描述: 对一些典型的弹靶同位旋与复合核同位旋相差较大的系统34S+244Pu→273Ds+5n(E*=50 Mev),二维主方程给出的蒸发剩余截面[49]与实验值[52]符合度很高,进而扩展了一维主方程适用的范围。 在重离子核反应过程中,原子核由于受到很强的核与库仑相互作用而变形,变形核的质量、核-核相互作用、库仑相互作用都会发生改变,这必然会影响随后的反应过程[53–55]。其中最重要的形变方式是四极形变,锕系靶核还具有较大的十六极形变[56]。 动力学形变影响弹靶相互作用的势垒高度,进一步影响耗散到系统中激发能的大小。不仅如此,在形成双核系统并发生核子转移后,类弹、类靶也会发生动力学形变,进而影响系统的演化过程[45]。因此,采用二维主方程,同时考虑动力学形变效应,可以得到“精确”描述反应机制的数值解。 图6.(a)48Ca+242Pu反应系统的驱动势在时间起点t=0 s和t=290×10−22 s处随质量不对称度的变化行为,(b)对比了仅考虑四极形变时的驱动势和同时考虑四极形变和十六极形变时的驱动势[56] 图6(a)描述的是反应系统48Ca+242Pu驱动势随双核系统质量不对称度η的变化情况。基于Fokker-Planck方程研究低能重离子碰撞中类弹、类靶四极形变随时间演化的结果,核的四极形变期待值随时间指数增加[55],最后达到平衡值。因此,考虑到驱动势随时间的演化行为,对图像作出以下说明。 由前面的讨论知,形成复合核需要克服内部熔合位垒(Bg点和入射点之间的差值)。在t=0 s时,图像为未考虑动力学形变驱动势随η的变化。根据t=290×10−22s的结果,表明考虑动力学形变后的内部熔合位垒更高,抑止重离子熔合而使得熔合几率变小[36]。图6(b)也呈现出类似的结果:同时考虑十六极形变时,系统内部熔合位垒会更高,驱动势在η的近对称区域内减小,增加准裂变发生的几率,不利于熔合过程进行。 基于动力学形变下的驱动势,计算二维主方程下对应的熔合几率。图7(a)中,GSD表示仅考虑基态形变计算的熔合几率,DyD表示考虑动力学形变后计算的熔合几率。对比发现,考虑动力学形变后的熔合几率减小,与之相应的蒸发剩余截面也减小。其中,考虑动力学形变后的计算结果在图7(b)实验测量数据的误差范围内。 图7.(a)靶核为242Pu反应系统熔合几率随激发能的关系,(b)靶核为242Pu反应系统蒸发剩余截面随激发能的关系,(c)靶核为244Pu反应系统熔合几率随激发能的关系,(d)靶核为244Pu反应系统蒸发剩余截面随激发能的关系[56] 图7(c)、(d)分别对比了仅考虑四极形变(β2)和同时考虑四极形变和十六极形变(β2+β4)两种情况的熔合几率和蒸发剩余截面随时间的变化。考虑十六极形变后的熔合几率和蒸发剩余截面显著减小,使得理论计算结果进一步符合实验数据。 二维主方程以质子数Z、中子数N为自由度,对一维主方程入射道在势能面较高位置作出修正。同时,考虑类弹、类靶核的动力学形变效应,结合四极形变的时间依赖性,可以帮助理论计算结果更好地再现实验测量值。除动力学形变的影响外,同位旋效应[49]、弹靶取向作用[57]对熔合几率的影响同样重要。 3.三维主方程 由二维主方程讨论知,采用类弹、类靶形变随时间演化的方法计算驱动势,可得到双核系统考虑动力学形变效应后的熔合几率与蒸发剩余截面。理论计算尽管可以很好地再现已发现的部分超重核,但对Z=119、120等更重的超重核的预言截面偏低[56],不利于实验上合成更重的超重核。 双核模型包含复合核演化过程中熔合与准裂变的竞争机制。目前,在低能重离子熔合反应过程中,准裂变是实验上可以直接测量的唯一信号,通过准裂变测量可以间接为熔合过程提供有效依据[45,58,59]。因此,进一步考虑动力学形变效应,研究熔合过程中的准裂变行为,可建立以质量不对称度η(或类弹质量数A1),与两核的形变自由度(β1,β2)三个宏观集体自由度的主方程: 对于任一双核组态(A1,β1,β2)下,准裂变碎片产额分布和熔合几率分别为[45]: 双核系统不仅可以通过转移核子向质量不对称度η方向演化,还可以在其动态形变空间(β1,β2)中演化。图8表示48Ca+248Cm系统相互作用势随质心距离的变化关系。 图8.双核组态相对于质心距离r的相互作用势[45] 图8表明,准裂变在双核系统演化的整个过程都时刻发生着。当双核系统沿质量不对称度方向增加至η=1时,两核组态在沿径向自由度r发展,越过相互作用势垒(准裂变势垒)发生准裂变。其中,图8中势阱为双核系统位置,势垒右侧为发生准裂变断点位置。 下面讨论仅考虑类弹、类靶对头碰撞的动态四极形变。通过数值求解三维主方程可知,双核组态(A1,β1,β2)在t时刻下的分布几率和准裂片碎片产额分布随时间的演化行为类似,表明双核系统的分布几率对准裂变产额分布起主要作用。 图9.E c.m=205 Mev下,反应道48Ca+248Cm关于质量不对称度的势能曲线[45] 图9表示质量数A1与双核系统最低能量的关系,即双核系统大致的的演化路径,其中蓝色箭头代表反应的起点。根据能量最低原理,双核系统沿能量最低的方向演化。因此,对某一特定的(A1,β1,β2)系统,质量不对称度η大致沿曲线路径进行演化。 图9黑线描述了双核系统驱动势随质量不对称度的变化关系,其中驱动势在沿质量不对称度减小的方向明显降低,即双核组态的分布几率在沿对称区域方向相对有所积累。图9红线描述了双核组态的准裂变势垒高度与质量不对称度的关系,在质量不对称度较大时,准裂变势垒较高,准裂变不易发生;在质量不对称度比较小(A1=100)时,准裂变势垒趋于零,准裂变易发生。除此之外,受准裂变的影响,双核组态的分布几率沿质量不对称度减小的方向会急剧减小。综合势能曲面与准裂变势垒高度这两方面的因素,双核组态的分布几率沿质量不对称度减小的方向先增大,当积累的速度等于双核组态因准裂变而流出的速度时,双核组态分布几率达到最大值,之后双核组态分布几率开始减小。 图10.E c.m=205 Mev下,反应道48Ca+248Cm准裂变碎片质量分布随相互作用时间的演化行为[45] 在得到双核系统状态的分布几率后,计算熔合反应过程中准裂变碎片的质量分布。图10表示不同时刻准裂变碎片的相对产额分布,在反应刚开始时(A1=48,A2=248),准裂变碎片产额集中在注入点附近,在t=50×10−22s时,准裂变碎片分布开始向质量对称的方向弥散,中等质量的准裂变碎片开始相对增多,在t=300×10−22s时,趋势几乎保持动态平衡不再改变。图像类似于一个具有两个峰值的倒置抛物线,同实验测量(黑线[60])的双峰位置和数值大小较好符合。 数值求解三维主方程很好地描述了准裂变碎片的相对产额。同时,在考虑动力学形变的基础之上,研究对熔合反应过程中平均总动能分布行为[45]等工作,可以验证熔合过程中“双核”组态存在的合理性,进而给出与模型自洽的结果,间接理解重离子熔合机制。 低能重离子核反应是研究超重核合成的一种有效机制,也是揭示完全熔合过程的一种重要方法。本文基于双核系统概念,发展了一个描述超重核形成机制的理论模型,即双核模型。该模型能够充分地体现重离子熔合过程中弹靶的结构效应,伴随着熔合过程中存在的问题,主方程经历了由一维至三维的变化,并在各个阶段取得了重要成果: 1.一维主方程选择质量数A为自由度,当弹核、靶核的中质比接近反应道复合系统的中质比时,讨论了熔合截面的弹靶组合相关性。但在弹核、靶核的中质比远离反应道复合系统的中质比时,由于中子和质子的转移情况比较复杂,计算结果存在2个量级的误差。 2.二维主方程以质子数Z和中子数N为自由度,考虑入射道在双核系统势能面较高的位置,对一维主方程进行修正。基于低能重离子碰撞中类弹(靶)四极形变随时间演化的结果,考虑了动力学形变效应,并对熔合几率和蒸发剩余截面进行了讨论。 3.三维主方程选择质量不对称度η、两核形变自由度(β1,β2)为自由度,进一步考虑动力学形变来描述准裂变的性质,结合实验上可测量准裂变信号的条件,使得双核系统能在更广的宏观系统组态范围内演化。 研究超重核的合成对探索原子核的质量数存在上限、检验和发展核结构理论模型有重要意义。对合成超重核的理论研究而言,描述熔合机制需做进一步研究,如发展多集体宏观变量主方程描述多核子转移反应[61–66]、较大反应Q值的近对称系统全熔合反应[67]等。除此之外,结合反应机制,需要从核结构[51,68]给出合适的裂变位垒、中子分离能及形变信息。最后,结合超重核的衰变[69,70]、结构理论,对核反应理论进行发展,给出最佳弹靶组合和最佳入射能量,为实现新核素提供可靠的理论预言。
III.双核模型
A.双核模型的两种解释
B.理论框架
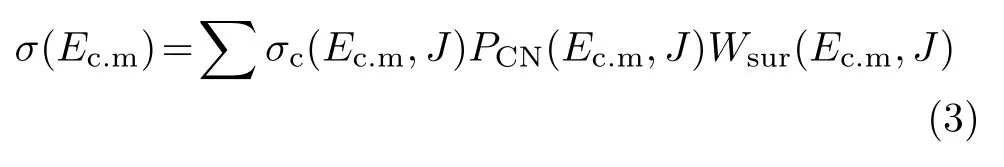
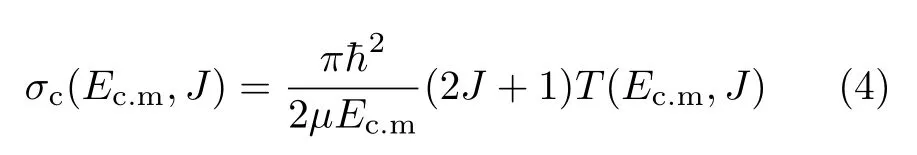
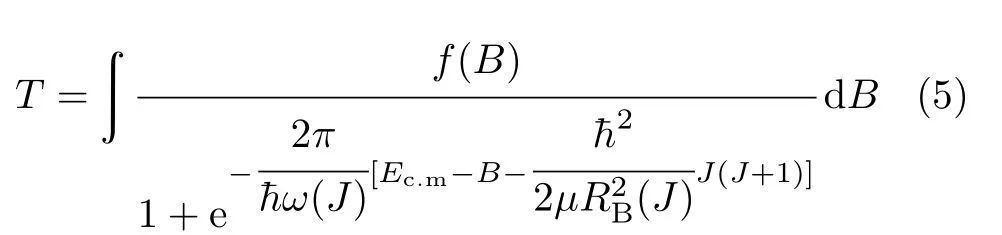
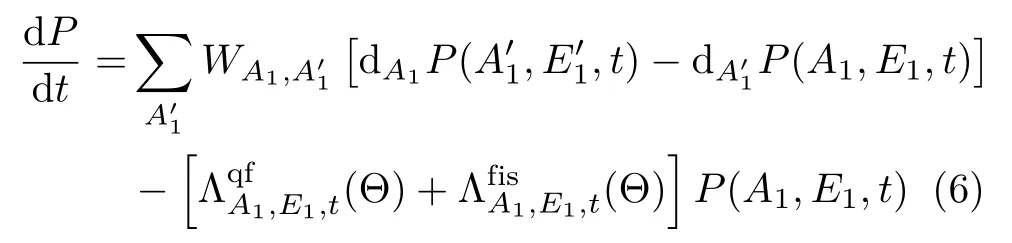

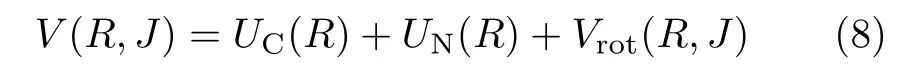
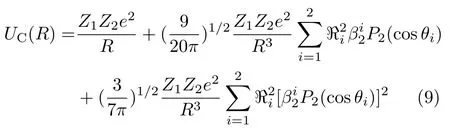
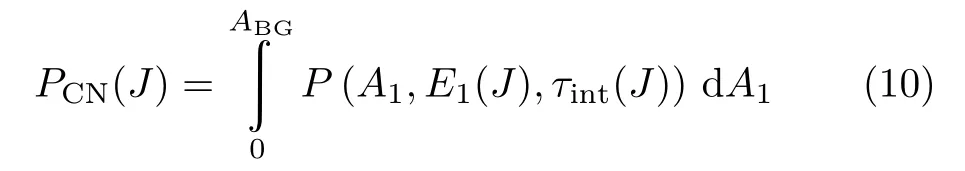
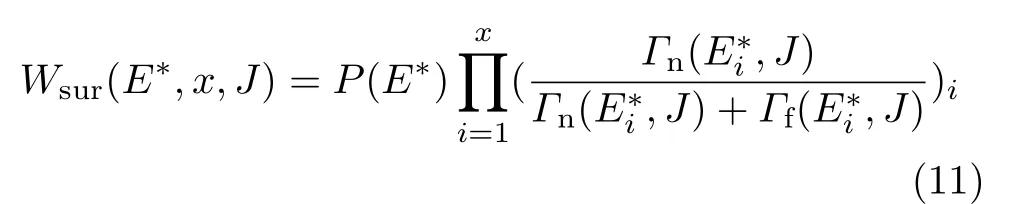
C.主方程发展
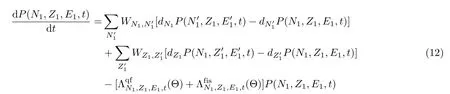
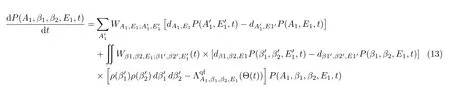

IV.总结与展望
