基于聚类分析的中国工业部门碳边际减排成本变化分析
2021-09-01
(浙江农林大学 经济管理学院,浙江 杭州 311300)
气候变化引起的温室效应作为当前全人类生存与发展所面临的重大挑战之一,已经受到世界各国的强烈关注,越来越多的国家加入到节能减排的行列中来。中国作为国际社会中负责任的一员,也对外公布了控制CO2等温室气体排放的总体目标,并实行碳排放管制,随之而来的是工业部门将逐渐承担温室气体的控制和减排成本,甚至可能造成产出减少、经济利润降低,严重的可能影响到经济增长[1]。近年来,政府大力倡导低碳发展理念,期望在减少排放的同时尽可能降低对经济的影响,增强可持续发展能力。[2]碳减排过程中的经济成本往往用“影子价格”来描述,但由于生产过程中排放的CO2本身不具备交易性质,[3]难以利用市场价格衡量其价值,因此,本文采用国际上较通用的环境方向性距离函数方法来估量CO2的潜在价格,以此直观地反映出不同经济体的减排潜力和实施成本,[4]即碳边际减排成本。
目前,中国正处于经济发展的紧要时期,能源消费已经超越美国,成为世界第一大CO2排放国,承受着巨大的国际压力。现有的减排政策和措施能在一定程度上缓解困境,但由于地域差异,各地在制定碳减排政策时必须综合考虑自身的经济条件和发展状况,因此明晰各地区工业部门的碳边际减排成本非常必要。一方面,测算碳边际减排成本有利于确定实施减排的重点地区;另一方面,能够帮助确立最优的减排路径,从而使减排工作所付出的成本尽可能最小化,而对测度结果进行聚类分析也能够更细致地为减排提供可靠的理论依据。鉴于此,本文将以全国29个省、市及地区工业部门的投入产出数据为基础,对碳边际减排成本进行测度并进行聚类分析,以期为相关决策部门制定科学的减排政策提供客观依据[5]。
一、研究方法与模型构建
(一)方向性距离函数参数法
本文将采用参数化方向性距离函数模型来对中国29个省、市及地区工业部门的碳边际减排成本进行测度。[6]该模型的基本思想是:在考虑期望产出增加的同时,兼顾了非期望产出的减少,只有当期望产出无法继续扩张、非期望产出无法继续减少时观测点才处于效率前沿。[7]这里假设,工业部门投入x∈R+N,期望产出y∈R+D,非期望产出c∈R+U,(y,c)隶属于生产集Ω(x),即(y,c)∈Ω(x),Ω(x) 为凸的、有界的闭集合。本研究将期望产出定义为工业部门总产值,非期望产出定义为 CO2排放,投入包括人力、资本和能源三个要素。[8]现假设投入x具有强可处置性,产出具有联合性,且联合具有弱可处置性,[9]则得到产出距离函数:
(1)
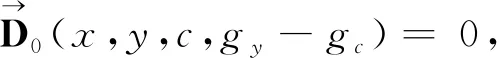
据此,我们可以计算出非期望产出(CO2)的影子价格,即边际减排成本:
(2)
在式(2)中,Pc表示工业部门碳边际减排成本(MAC),Py表示工业部门期望产出y的市场价格,D0表示工业部门投入产出向量,∂表示偏导数,g表示工业部门产出变量,x表示工业部门的投入,y表示工业部门期望产出(产值)的产量,c表示工业部门非期望产出(CO2)的产量。
(二)聚类分析与判别分析
利用K-Means算法对上述测算得到的碳边际减排成本数据进行聚类分析,[10]以寻求各地区工业部门碳边际减排成本的变化规律。
判别分析(DiscriminantAnalysis)是指按照一定的判别准则,建立一个或多个判别函数,[11]用研究对象的数据资料确定判别函数中的待定系数,并计算判别指标。[12]以此判定某一未知样本地区属于何类。
(三)数据来源
鉴于各地区统计局公布数据时间不一致,部分地区出现关键数据缺失的情况,这里只选取数据较为完整规范的29个地区作为研究样本。通过2008-2017 年全国29个省、市及地区的《统计年鉴》,选择规模以上工业部门的3个投入指标(工业部门固定资产、工业部门从业人员和工业部门能源消耗)和2个产出指标(工业部门总产值和工业部门CO2排放量),并对个别地区的缺失数据进行推算,最后根据《综合能耗计算通则》里的折算系数对不同能源进行标准煤折算。通过数据的收集和整理,样本期内全国29个省、市及地区碳减排行业 CO2排放情况如表 1 所示。
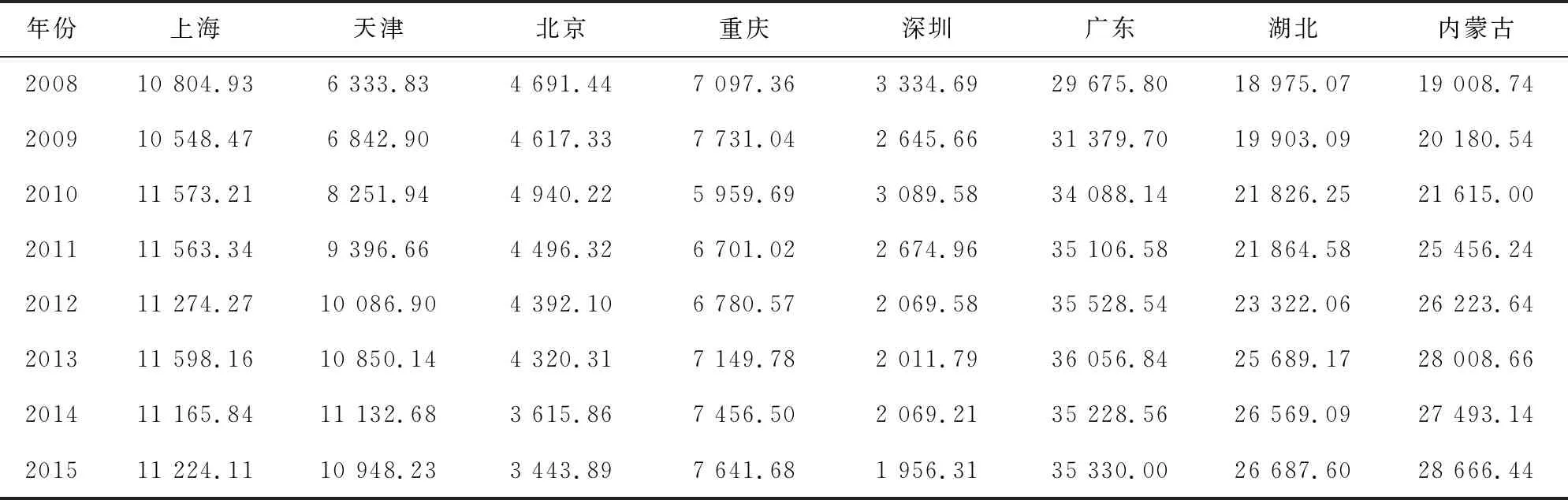
表1 2008-2017年全国29个省、市及地区工业部门CO2排放情况(万吨)
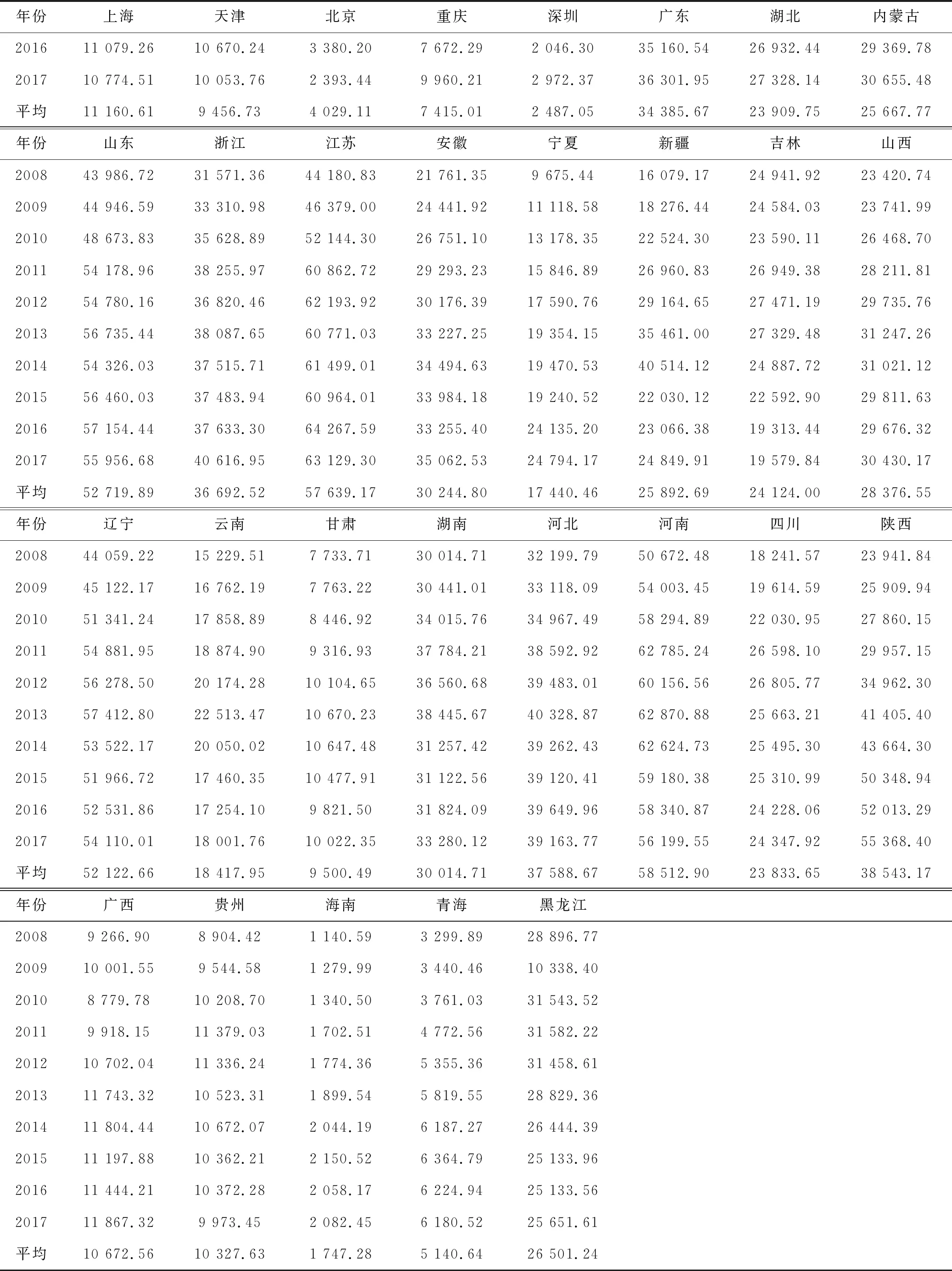
续表1
二、测度29个省、市及地区工业部门碳边际减排成本
本文的碳边际减排成本,是通过减少1单位的CO2排量所造成的损失,即运用CO2的影子价格来衡量,由于CO2排放量降低产出也随之降低,因此测度结果均为负值。通过原始数据的收集整理,运用式(2)方向性距离函数的环境生产函数求偏导,即解得CO2(非期望产出)的边际减排成本,[13]具体见表2。
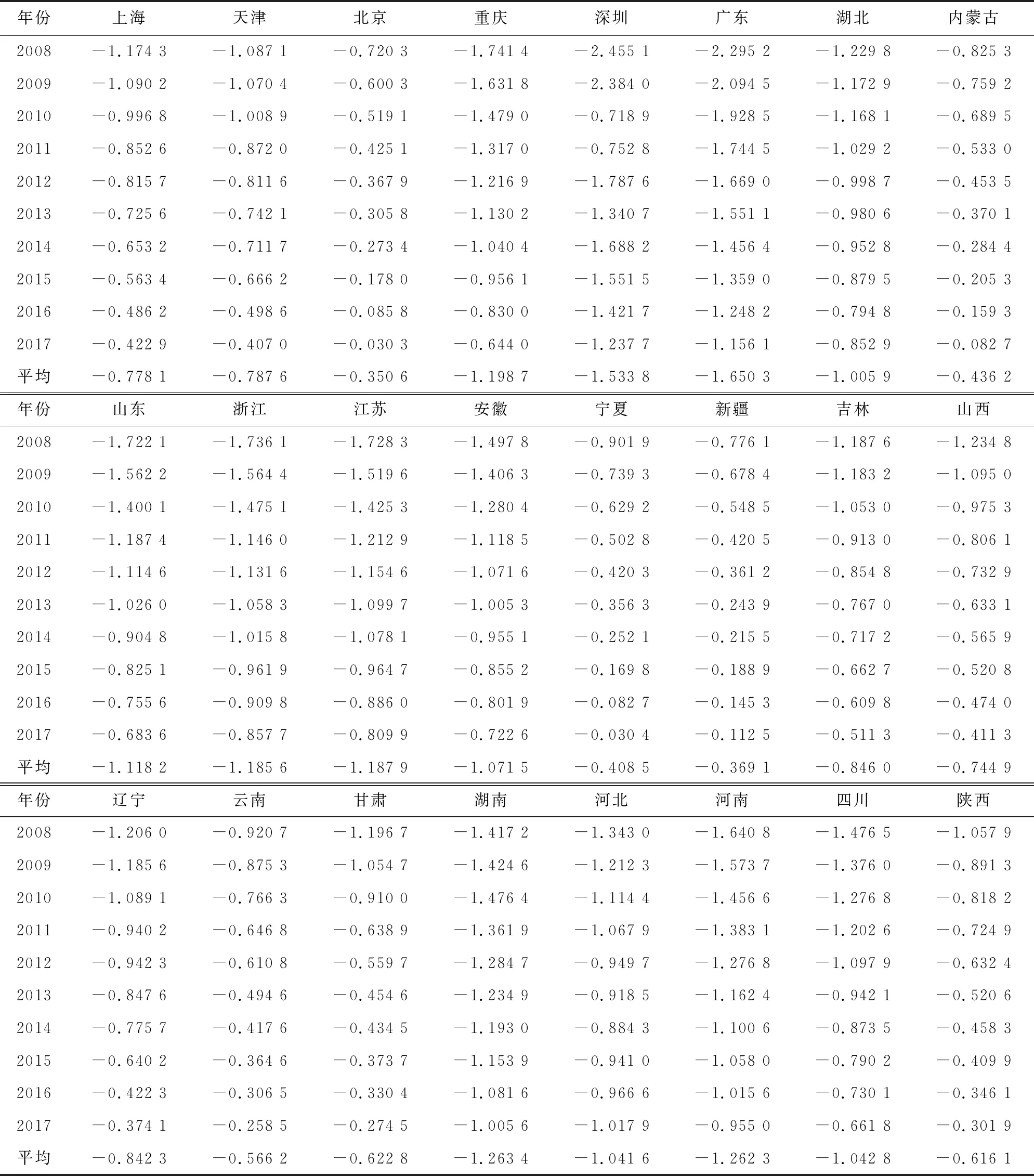
表2 2008-2017年样本单位工业部门碳边际减排成本(万元/吨)
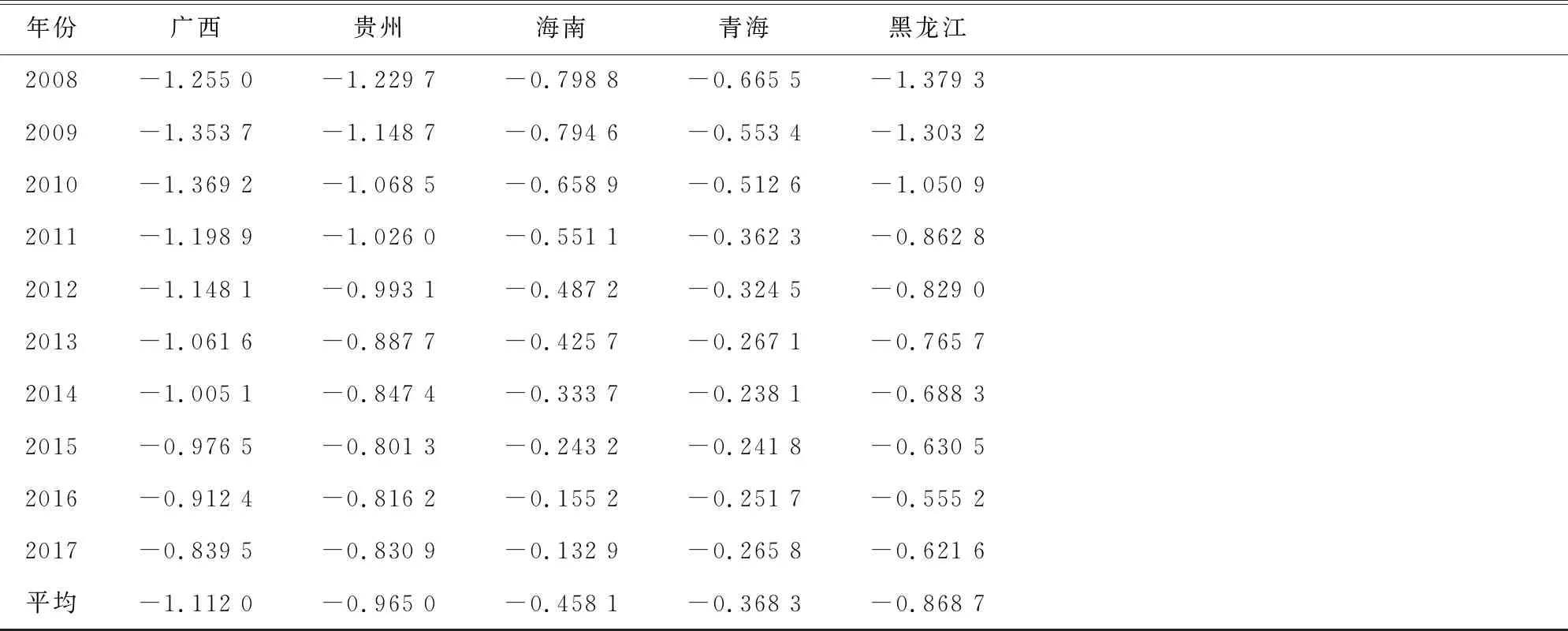
续表2
由于不同地区的资源禀赋、技术条件、发展路线等方面的不同,工业部门的碳边际减排成本参差不齐。以地区序列横向观测发现,10年间全国29个省、市及地区工业部门CO2的边际减排成本平均值存在很大的波动,整体没有明显规律。其中,广东省的碳边际减排成本平均值为1.650 3万元/年,这说明10年间广东省的工业部门平均每减少一吨CO2就需支付减排成本1.650 3万元。测度结果显示,东部经济发展较快的地区工业部门碳边际减排成本普遍较高。
以时间序列纵向观测发现,10年间样本单位碳边际减排成本极少数地区出现轻微增长,整体呈稳定下降趋势。
三、对29个省、市及地区碳边际减排成本的分类分析
(一)聚类分析
为进一步探索全国29个省、市及地区工业部门的碳边际减排成本的变化规律,这里对表2的数据进行聚类分析。在聚类分析中,假设样本期内全国29个省、市及地区工业部门的碳边际减排成本分别为bi,i= 1,2,…,29,即bi=b1,b2,…,b29(1-29分别代表:深圳、广东、上海、天津、重庆、湖北、山东、浙江、江苏、安徽、吉林、辽宁、湖南、河北、河南、贵州、四川、山西、广西、黑龙江、北京、云南、甘肃、海南、青海、陕西、宁夏、新疆、内蒙古),Ct为分类,t为需求空间的分类数。
对表2数据进行K-means聚类,聚类结果表明:10年间各地区工业部门的碳边际减排成本分为3类比较合适,即t=3,此时Kaiser-Meyer-Olkin= 0.840,大于 0.5,巴特利特球体检验P= 0.000,小于 0.05,说明该分类合理,适合作聚类和判别分析。聚类结果见表3,Kaiser-Meyer-Olkin检验结果见表4。
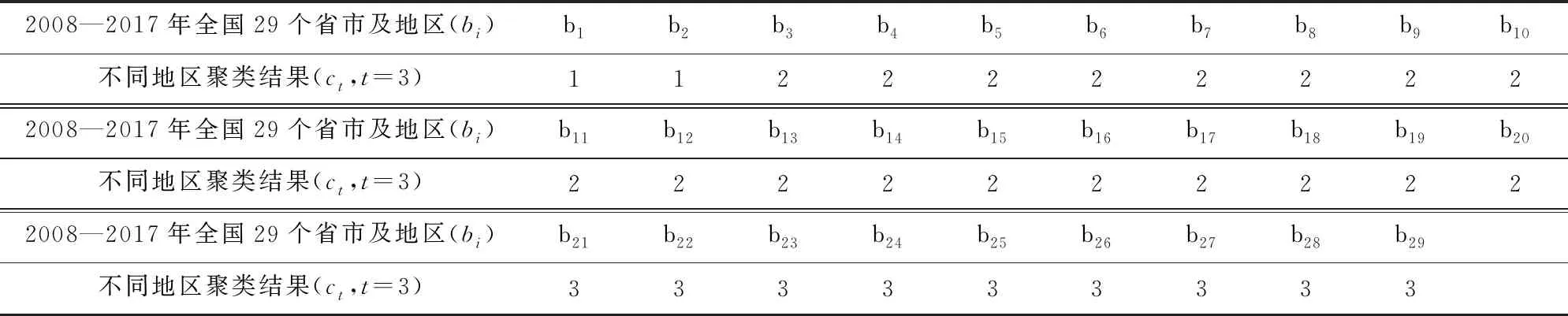
表3 2008-2017年全国29个省、市及地区工业部门碳边际减排成本聚类结果

表4 KMO与Bartlett检验
表5显示各变量均通过显著性检验,聚类结果合理,真实反映了29个样本地区工业部门碳边际减排成本的变化情况。
(二)判别分析
采用判别分析的方法为上述聚类结果建立判别方程。判别分析的基本模型为:
其中:y表示判别函数值;xi表示变量;bi表示判别系数;i= 1,2,…,k表示判别变量的个数。
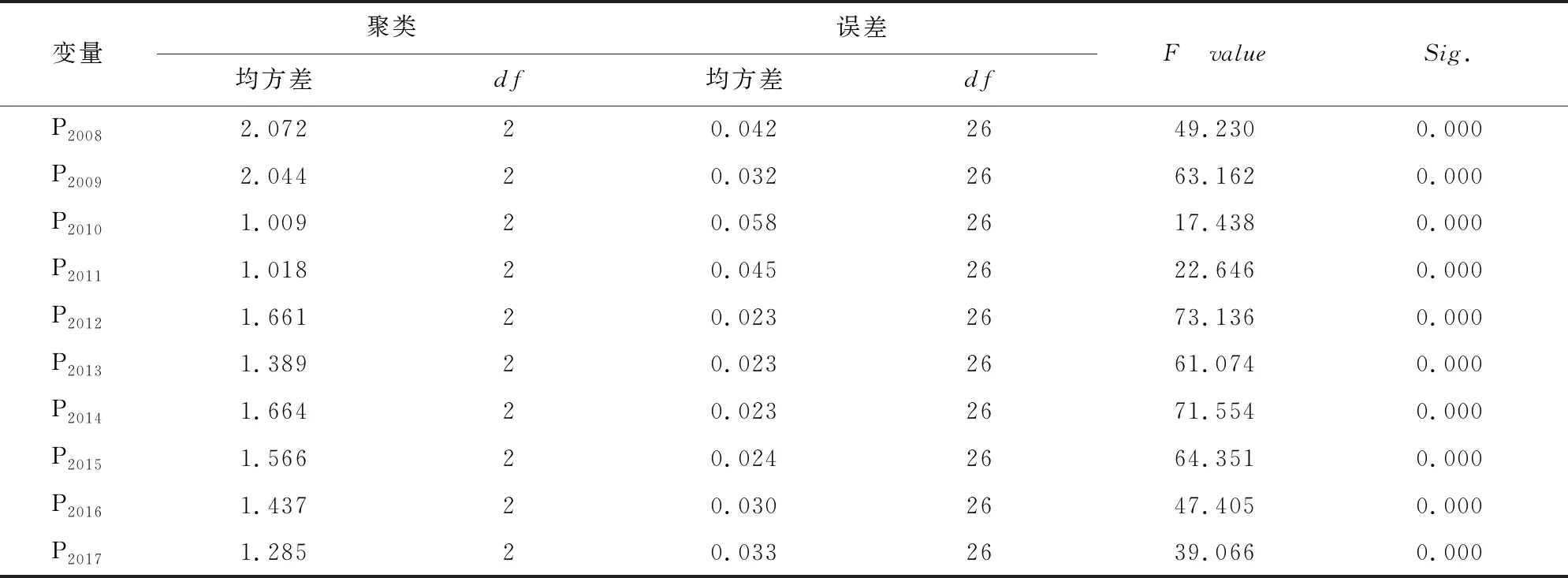
表5 聚类分析的方差分析表( ANOVA)
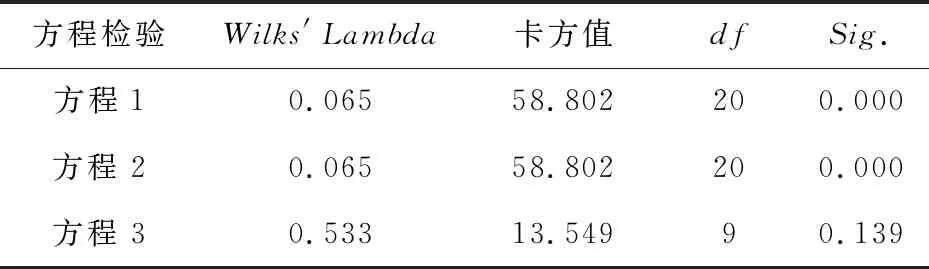
表6 判别分析的威尔克Lambda检验
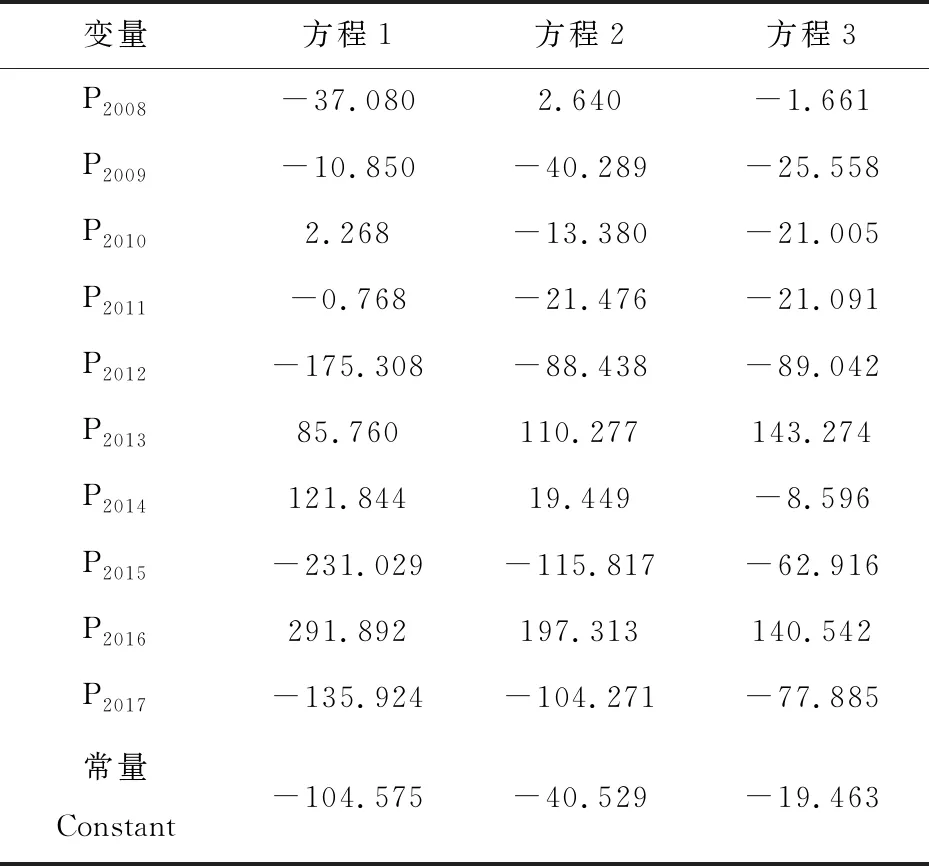
表7 采用强入法所求判别方程的系数
这里首先采用强入法进行判别,判别分析的威尔克Lambda检验结果见表6。从表6的威尔克Lambda值可以看出,方程1、方程2 的威尔克Lambda=0.065,接近于 0,其Sig.=0.000,小于0.05,说明第1、2个判别方程均有统计学意义。第3个判别方程的威尔克Lambda值为0.533,接近于1,其显著性检验Sig.= 0.139,大于 0.05,说明该方程的统计学意义不大,需要通过逐步判别法进一步分析。判别分析的系数见表7,判别方程具体形式见式(3)。
y1=(-104.575)+(-37.080)P2008+(-10.850)P2009+2.268P2010+(-0.768)P2011+(-175.308)P2012+85.760P2013+121.844P2014+(-231.029)P2015+291.892P2016+(-135.924)P2017
y2=(-40.529)+2.640P2008+(-40.289)P2009+(-13.380)P2010+(-21.476)P2011+(-88.438)P2012+110.277P2013+19.449P2014+(-115.817)P2015+197.313P2016+(-104.271)P2017
y3=(-19.463)+(-1.661)P2008+(-25.558)P2009+(-21.005)P2010+(-21.091)P2011+(-89.042)P2012+143.274P2013+(-8.596)P2014+(-62.916)P2015+140.542P2016+(-77.885)P2017
(3)

表8 逐步回归的威尔克Lambda检验
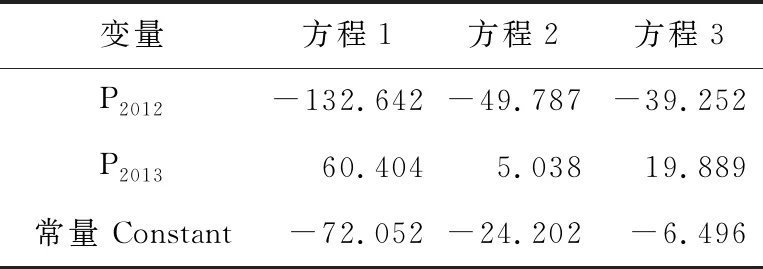
表9 逐步回归法所求判别方程的系数
采用逐步回归法所求判别方程的威尔克Lambda检验结果见表8,判别方程系数见表9所示。因此,采用逐步回归的方法求得29个省、市及地区工业部门碳边际减排成本分类判别的最终判别方程如式(4)。
(4)
从方程结果不难发现,10年间29个省、市及地区工业部门的碳边际减排成本存在较大的波动,且明显可以分为 3个区:深圳市、广东省为分区1,碳边际减排成本较大;上海市、天津市、重庆市、湖北省、浙江省、山东省、山西省、江苏省、安徽省、吉林省、辽宁省、湖南省、河北省、河南省、广西壮族自治区、贵州省、黑龙江省、四川省为分区2,碳边际减排成本处于中等水平;北京市、宁夏回族自治区、新疆维吾尔自治区、云南省、甘肃省、海南省、青海省、陕西省、内蒙古自治区为分区3,碳边际减排成本较低。由最终判别方程可以发现,2012、2013年的碳边际减排成本数据对分区影响最显著。
另外,3个判别方程的全部样点回代检验的准确度均为100%,说明该判别方程具备一定的可信度。同时,也一定程度上反映了3个分区碳边际减排成本的规律性。事实上,发展路线、技术条件、资源禀赋、地理位置及产业结构的不同,也在一定程度上造成了3个分区碳边际减排成本的差异,如何平衡CO2减排与经济增长之间的矛盾也是当前面临的重要问题。
四、结论与建议
(一)结论
文章根据收集整理的2008-2017年间中国29个省、市及地区《统计年鉴》中工业部门的投入产出数据,利用方向性距离函数模型求得工业部门的碳边际减排成本,并采用聚类分析对该数据的变化情况进行了聚类和判别,得出以下结论。
1.29个省、市及地区工业部门的碳边际减排成本存在明显的地区性波动,且无明显规律。经济较发达的地区碳边际减排成本相对较高,经济欠发达地区碳边际减排成本相对较低,二者呈正相关关系。减排成本的高低将直接影响工业部门对后续减排路径的选择。[14]
2.聚类分析结果表明:2008-2017年间29个省、市及地区工业部门的碳边际减排成本可以分为3个分区,其中广东省与深圳市作为分区1,其样本期内碳边际减排成本平均值为1.59万元/吨;上海市、天津市、重庆市、湖北省、山东省、浙江省、江苏省、安徽省、吉林省、辽宁省、湖南省、河北省、河南省、贵州省、四川省、山西省、广西壮族自治区、黑龙江省为分区2,碳边际减排成本处于中等水平,平均值为1.18万元/吨;北京市、云南省、甘肃省、海南省、青海省、陕西省、宁夏回族自治区、新疆维吾尔自治区、内蒙古自治区为分区3,碳边际减排成本较低,平均值为0.51万元/吨。由最终判别方程可知,2012、2013年的碳边际减排成本数据对分区影响最为显著。总体来看,分区1的东部地区经济较发达,碳边际减排成本相对较高;分区2的中东部地区经济发展状况与碳边际减排成本均处于中等水平;分区3为西部欠发达地区,工业发展较缓,碳边际减排成本也相对较低,该结果与地区间经济发展水平基本吻合。
(二)建议
根据分区结果可以明确的是,国家在制定减排政策和减排目标时应该因地制宜,不可等量齐观。对于经济较发达且碳减排成本较高的分区1,应设置较高的减排目标,对于碳减排成本处于中等的分区2应设置相对中等的减排目标,而经济欠发达的分区3应将其发展权置于首位,设置相对较低的减排目标,从而使3个分区在完成各自碳减排目标的同时尽可能缩小对经济发展的影响。这里提出以下建议。
1.分区1应严控CO2增量,控制高耗能与碳排放高的行业过快增长。充分发挥碳交易市场的减排效应,同时调整和优化产业结构,[15]积极推进能源结构调整。
2.分区2应加强宣传,提高减排意识,健全法律法规。加大监督执法力度,强化减排管理,切实保障减排政策效应的可持续性;积极推动和完善利于减排的政策,形成激励和约束机制。
3.分区3应增加研发资金投入,鼓励技术革新。在减排过程中政府应增加减排行业研发资金的投入,鼓励和支持CO2排放高的行业进行技术革新,促进实现绿色发展[16];同时,完善碳交易市场机制,对西部减排行业实施一定比例的优惠政策,从而实现减排目标,推动经济健康可持续发展。
