微动工况下裂纹扩展仿真分析*

赵一舟，李 俨，土 旗，唐正强

(贵州大学机械工程学院，贵阳 550025)

0 引言

在材料加工与实际应用过程中，不同材料会因自身存在不同缺陷导致材料内部结构出现裂纹、裂缝等微动疲劳现象[1]。裂纹、裂缝的产生会随时间与外载荷作用下在材料中继续扩展，在内部结构中产生断裂失效以致急速降低结构使用寿命[2-4]。

微动疲劳现象通常发生在微、纳米量级的相对运动和交变载荷同时作用下的两个紧密接触物体之间[5]。文献[6-8]认为在一定条件下，结构脆性断裂问题中材料本身所具有微裂纹、裂缝等微动疲劳缺陷会诱导裂纹的萌生、扩展，降低工件的疲劳寿命，造成工件的断裂破坏。构件本身所固有的组织缺陷或加工所造成的损伤会产生初始裂纹，初始裂纹在相对运动和交变载荷的共同作用下发生扩展导致构件的断裂破坏[9]。本文将基于Python二次开发利用ABAQUS自带的围线积分算法和对网格重划分程序的编制对微动工况下的裂纹扩展进行建模分析。对微动情况下多裂纹任意路径扩展进行模拟，对不同往复位移幅值和不同下压深度下的裂纹扩展进行模拟，以探究不同往复位移幅值和不同下压深度对多裂纹扩展的应力强度因子、裂纹扩展结果与最终扩展轮廓等影响。

1 向量式有限元法基本理论

1.1 多应力裂纹判定依据

在研究裂纹扩展规律时，常把构件中各种因素导致裂纹产生原因根据初始裂纹不同的特点简化为三种基本类型，如图1所示：I型(裂纹面和裂纹所受拉应力呈现，使初始裂纹面角度呈扩大趋势并且裂纹向里扩展)；II型(受到垂直于裂纹前沿且平行于裂纹面的剪切应力，使在平面内裂纹面有相对滑开的趋势)；III型(受到剪切应力分别平行于裂纹前沿和裂纹表面，使裂纹面有相对错开的趋势)[10]。

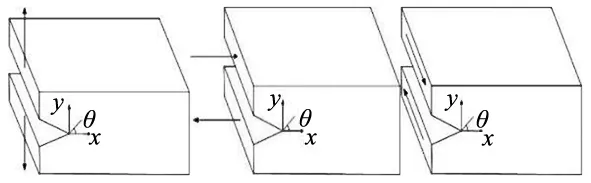
(a)I型 (b)II型 (c)III型

在实际工程中，裂纹形式多以复合型存在，多数处于三种复合型的变形状态。复合型裂纹的开裂条件较为复杂，且一般不按照裂纹的原方向进行扩展，其外载荷作用时不对称，初始裂纹的角度不对称，还有材料为各向异性等情况[11]。

1.2 应力强度因子计算

为了反映裂纹尖端应力以及应变变化快慢与变形程度，本文基于应力外推法计算裂纹尖端的应力强度因子值，再通过应力强度因子来判定裂纹是否能够扩展以及扩展角度[12]。首先，依次提取裂纹尖端位置、拟合点应力与位置；其次，计算拟合点与裂纹尖端距离；将计算出的距离带入公式得到拟合点应力强度因子；再次，根据所得强度因子绘制出拟合点与拟合曲线；最后，输出拟合曲线与y轴交点值，即反映裂纹尖端弹性应力场强弱的物理量称为裂纹尖端应力强度因子，其中K1与K2对应I型与II型裂纹应力强度因子。

利用前处理中储存单元节点等信息，提取出需进行拟合的点j坐标(xj,yj)、裂纹尖端节点i坐标(xi,yi)和非奇异节点应力值σyj[13]。其中应力强度因子值计算过程如下[14-15]：

(1)计算裂纹尖端和拟合点之间距离rj：

(1)

(2)计算拟合点应力强度因子：

(2)

(3)构造出数据对(rj，KIj)，利用最小二乘法拟合数据点。在断裂力学中假设KIj和rj之间的关系可利用线性函数进行拟合近似，则有：

(3)

(4)

(5)复合裂纹最大能量释放率的方向为裂纹扩展的方向，裂纹开裂角为最大周向应力的方向角θmax，裂纹扩展角度为：

(5)

2 模型建立与数值模拟

2.1 有限元模型

如图2所示为微动工况下裂纹预置模型，在平板上预置多条裂纹，并且在半圆面设置竖直向下载荷作用在下端平板面上，当半圆面和平板面接触时半圆面保持下压同时进行微小幅度的往复运动，以此在平板面上产生作用力，在竖直载荷和往复运动的共同作用下裂纹发生扩展。

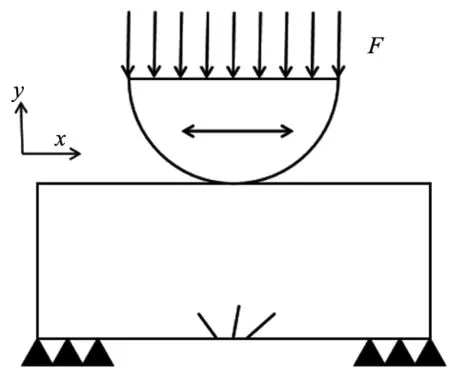
图2 裂纹扩展前处理多裂纹模型图

取球直径为20 mm，平板长为30 mm，宽为10 mm。预制裂纹长度分别为1.8 mm、2 mm和1.2 mm(从左到右的顺序)，预置裂纹角度分别120°、85°和45°(从左到右的顺序)，弹性模量为73 000 MPa，泊松比为0.33。在此多预制裂纹模型基础上，分别对不同往复位移幅值和不同下压深度展开研究，将所得到数值进行模拟并分析。

2.2 数值模拟流程

裂纹扩展模拟流程图如图3所示，Python程序原理是基于ABAQUS二次开发的围线积分和网格重划分实现任意路径的裂纹扩展模拟。操作步骤为：先在ABAQUS经典界面建立裂纹扩展前几何模型，对模型所需单元节点信息进行导入；再对建立完成后的几何模型进行材料属性的设置与分配；将材料属性设置完成后的几何模型装配成独立的实体装配体；定义模型中半圆面施加边界条件、载荷和定义预制裂纹等，使其与平板能够相互作用；然后利用Python调用ABAQUS自带的围线积分算法，加入最大周向应力法则判定裂纹扩展，找到新的裂纹尖端；再删除网格，重新利用围线积分算法进行几何模型的切分；最后切分好之后再重新进行网格的划分，独立完成整套流程后，再一直循环这一系列步骤直到裂纹判定不扩展为止，程序循环结束。

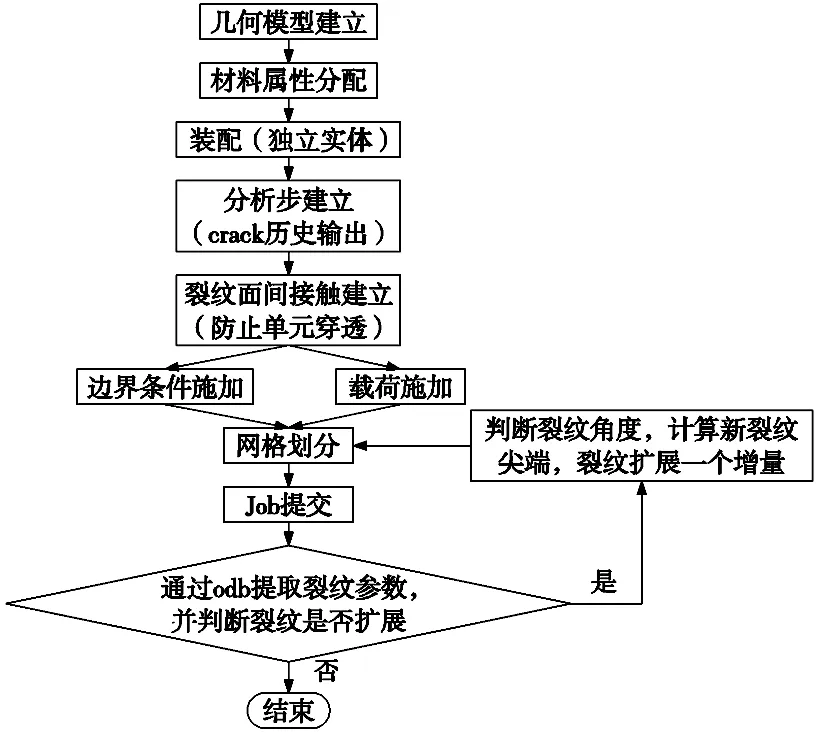
图3 裂纹扩展模拟流程图

3 裂纹拓展结果分析

3.1 微动幅值对多裂纹扩展的影响

根据图2所述模型，设置此多条预制裂纹下压深度为1 mm，往复运动距离分别为2 mm、4 mm、6 mm、8 mm进行结果分析。裂纹扩展结果应力图如图4所示。分析应力结果对比图中裂纹扩展情况，多裂纹扩展时往复运动的不同对裂纹扩展没有造成太大的影响，裂纹扩展路径基本一致。

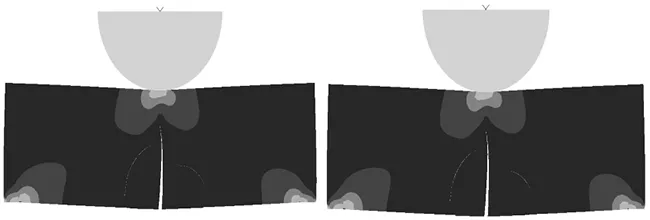
(a)位移幅值为2 mm (b)位移幅值为4 mm

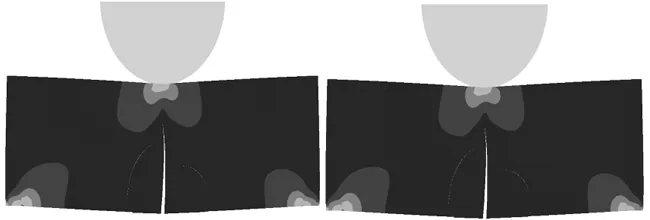
(c)位移幅值为6 mm (d)位移幅值为8 mm

如图5所示是不同位移幅值下三条裂纹应力强度因子K1对比图(L1、L2、L3分别对应从左到右裂纹)。可看出左边和右边的裂纹趋势均是先增大到一个最大值，然后缓慢下降到0，此时裂纹停止扩展；中间裂纹扩展时应力强度因子K1呈现出直接缓慢下降到0的趋势，这是因为多裂纹情况下，中间裂纹受到两边裂纹应力场的同时作用，会对中间裂纹所受应力造成干扰，但大致趋势没有改变。图中还可看出，多裂纹扩展时不同往复位移幅值对应力强度因子K1所造成的影响可忽略不计，应力强度因子K1几乎没有变化。

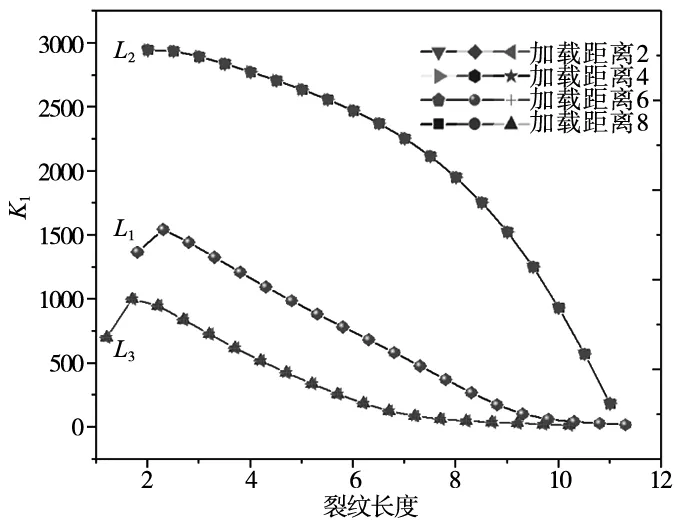
L1：左边裂纹 L2：中间裂纹 L3：右边裂纹

不同位移幅值下三条裂纹应力强度因子K2对比图(L1、L2、L3分别对应从左到右的裂纹)如图6所示，可看出左边裂纹应力强度因子K2从开始的正值突变到0，然后稳定在0值附近；右边裂纹应力强度因子K2从开始的负值突变到0，然后稳定在0值附近。是因为这两条裂纹在最开始会出现方向上的突变，所以K2值也会出现突变的变化，后期是因为在突变后裂纹变成了I型裂纹，裂纹扩展条件变成由K1主导；而从正值与负值的突变是因为两条裂纹转动方向不同，所以值会有相反性差异；并且K2值在0值附近会有震荡产生，是由于多裂纹扩展时裂纹应力场之间会相互影响，造成K2值震荡；而中间裂纹应力强度因子K2值起伏变化较大，先是突变到最大值再出现起伏震荡，是因为中间裂纹应力场受到两端裂纹干扰，会造成方向上的变化；同时，不同位移幅值对应力强度因子K2值影响可忽略不计。

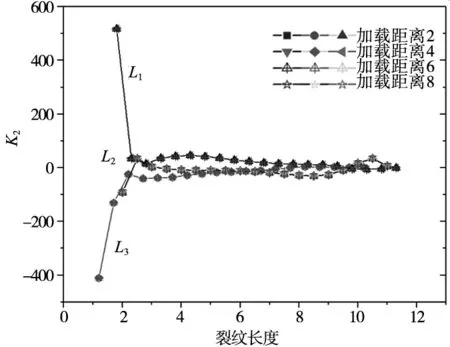
L1：左边裂纹 L2：中间裂纹 L3：右边裂纹

不同位移幅值下三条裂纹新的裂尖点所拟合而成的图像(L1、L2、L3分别对应从左到右的裂纹)如图7所示，即为裂纹扩展最终图像。可看出，左边裂纹扩展轮廓有细微差别，往复运动为4 mm时裂纹轮廓出现变化，并且裂纹扩展比2 mm、6 mm、8 mm多一步，是因为往复运动的不同造成了影响，而中间和右边裂纹在往复位移幅值改变条件下的变化可忽略不计；往复位移幅值不同并没有对裂纹扩展的最终轮廓造成太大影响，即不会对新裂尖位置造成太大影响。

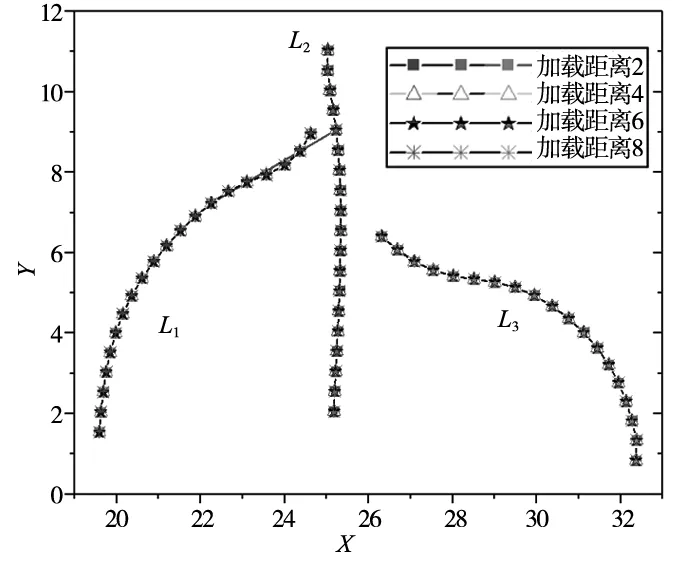
L1：左边裂纹 L2：中间裂纹 L3：右边裂纹

3.2 多裂纹扩展不同下压深度结果分析

根据图2所述模型，设置多条预制裂纹进行往复运动距离为2 mm,下压深度分别为1 mm、2 mm、3 mm进行结果分析，裂纹扩展结果应力如图8所示。

(a)下压深度为1 mm

(b)下压深度为2 mm

(c)下压深度为3 mm

可看出多裂纹扩展时不同下压深度对裂纹扩展规律有较大影响，下压深度越深裂纹扩展最终结果张开幅度越大。但对比下压深度为2 mm和3 mm时，幅度变化不明显，是因为一定程度后，张开幅度变化可忽略不计。

不同下压深度三条裂纹应力强度因子K1对比图如图9所示，可看出左边和右边的裂纹趋势同样是先增大到最大值后再缓慢下降，但没有完全趋近于0。是因为裂纹扩展到最后，两边裂纹和中间裂纹出现交叉，裂纹被迫停止扩展。中间裂纹扩展时应力强度因子K1呈现出直接缓慢下降到0的趋势，是因为中间裂纹受到两边裂纹应力场同时作用，对所受应力造成干扰。可看出裂纹之间出现交叉情况时，裂纹会直接停止扩展，此时K1值不一定趋近于0。同时，下压深度越深时裂纹区域所受应力越大，应力强度因子K1值越大，这一现象符合实际工况。

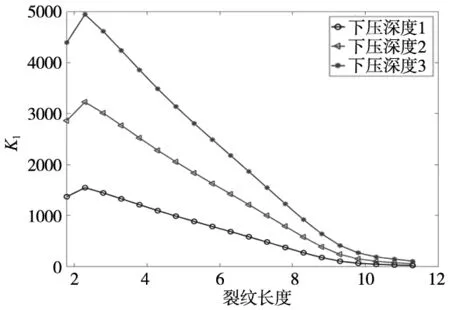
(a)左边裂纹扩展结果K1对比图

(b)中间裂纹扩展结果K1对比图

(c)右边裂纹扩展结果K1对比图图9 不同下压深度扩展结果K1对比图

不同下压深度三条裂纹应力强度因子K2对比图如图10所示。

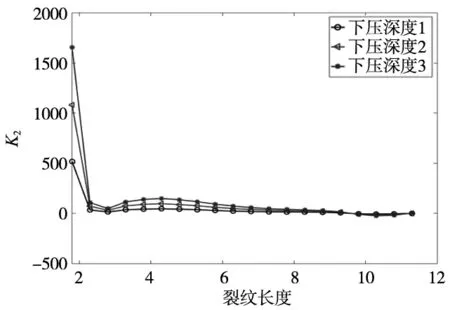
(a)左边裂纹扩展结果K2对比图

(b)中间裂纹扩展结果K2对比图

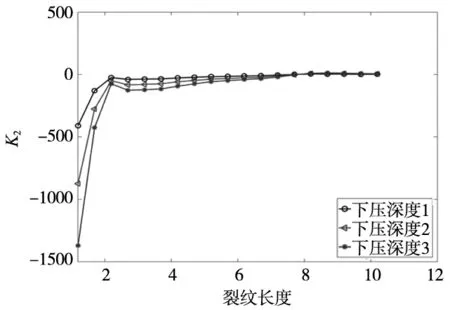
(c)右边裂纹扩展结果K2对比图图10 不同下压深度扩展结果K2对比图

可看出左边裂纹应力强度因子K2从最开始正值突变到0后稳定在0值附近；右边裂纹应力强度因子K2从最开始负值突变到0后稳定在0值附近。是因为最开始两条裂纹有方向上的突变，所以K2值也有较大的变化；突变后裂纹变成了I型裂纹，裂纹扩展条件变成由K2主导；同时，会因为两条裂纹转动方向不同，值的正负会有相反性差异。中间裂纹应力强度因子K2值则产生剧烈震荡，先突变且不稳定在0处，是因为中间裂纹应力场受到两端裂纹干扰，K2值变化造成方向变化；下压深度越大裂尖所受应力越大，K2值先增大，再减小稳定在0值附近，变成由K1主导的裂纹，这一现象符合实际工况。

不同下压深度下三条裂纹新的裂尖点所拟合图像如图11所示，即为裂纹扩展最终图像。

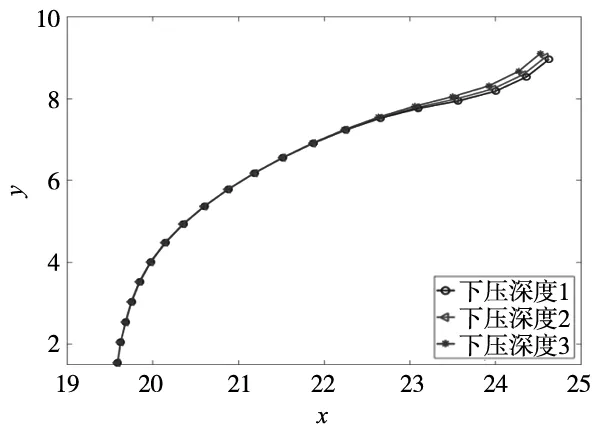
(a)左边裂纹扩展最终轮廓对比图

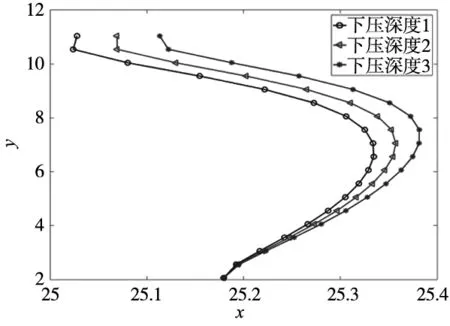
(b)中间裂纹扩展最终轮廓对比图

(c)右边裂纹扩展最终轮廓对比图

可看出，下压深度越大对裂纹扩展最终轮廓造成影响越大。下压深度越大裂纹弯曲角度越大，是因为应力不再向两边集中，中间区域产生应力越大，裂纹轮廓y值越大。相对于左边和右边裂纹，中间裂纹最终轮廓影响最大，是因为下压深度越大应力越集中，在接近平板中间区域最为明显，故裂纹中间区域的变化程度最大。

4 结论

本文通过有限元围线积分模拟微动情况下多裂纹的任意路径扩展，模拟往复运动情况下多裂纹任意路径扩展对不同往复位移幅值和不同下压深度应力强度因子K1、K2值和裂纹最终扩展轮廓对比，研究结论如下：

(1)相同下压深度不同往复位移幅值时：对裂纹扩展影响可忽略不计，例如应力强度因子K1和K2值不会因裂纹条数增加产生明显变化。同时，三条裂纹在往复位移幅值改变条件下变化忽略不计，且不会对裂纹扩展轮廓造成太大影响；

(2)相同往复位移幅值不同下压深度时：一定范围内下压深度越大，裂纹区域所受应力也越大，裂纹扩展的各项参数以及最终扩展轮廓变化越明显；

(3)除下压深度与往复位移带来的影响，裂纹与裂纹之间的应力场也会相互作用，对裂纹各项参数造成影响，导致参数数值上下波动。另外，多裂纹扩展时，当裂纹路径产生交叉，裂纹扩展过程会立即结束。