多变量时序关联分析的跌倒预测算法

2021-08-31朱文辉李伟代勇

电子测试 2021年17期

朱文辉，李伟，代勇

(1.黑龙江科技大学电气与控制工程学院，黑龙江哈尔滨150022；2.哈尔滨工业大学机电工程学院，黑龙江哈尔滨,150001)

0 引言

伴随着现代化进程与社会进步，人口老龄化在全球成为普遍现象。中国拥有全世界最庞大的老年人群体[1]。根据国家统计局发布的数据，2019年末，中国的65岁及以上老年人口达到1.76亿人，占总人口的12.6%[2]。人口老龄化问题带来诸多社会问题。老年人属于易摔倒人群，老年人的骨质密度越来越低，甚至变得脆弱，很容易因为意外发生导致骨折，若髋部骨折发生在老年人身上，其死亡率比癌症还要高，其后果将给家庭带来严重的经济负担，并已引起业界的高度重视[3]。在不影响老年人正常活动为前提，通过科学手段及时预测老年人摔倒并利用快速保护装置避免髋骨碰撞造成伤害，可以有效减小老年人摔倒带来的健康伤害和医疗支出，现已成为国际上新的研究热点之一[4]。便携式高速充气式气囊是跌倒时最有效的保护装置，体积小、重量轻、适合随身穿戴。当发生跌倒，身体的髋关节在触地之前，这个过程的持续时间大概为0.8秒左右，在这期间需要让气囊引爆展开，现有的高速气囊展开时间在0.1秒左右，所以在作出跌倒预测结果输出时间越提前，气囊保护的效果就越好。

现有最常见的检测人体运动行为的方法是通过采集人体线加速度及角速度信息并通过实验设定其阈值来检测佩戴者是否有摔倒行为发生，例如哈尔滨工业大学的闫俊泽等[5]设计一种由三轴加速度计和三轴陀螺仪组成的装置佩戴于人体胸部和大腿部，并通过实验设置两部位各自的合加速度和角速度阈值，达到92%的检测率并具备较强的时效性。韩国的Amit等研究了一款佩戴于人体胸部的跌倒探测系统，它是由加速度传感器、陀螺仪、倾角传感器组成，如果人体的胸部角度变化70°，并且加速度变化非常剧烈则认为人体摔倒。实验证明它对前后摔倒具有较高的敏感性，但是对左右的方向的摔倒却不够敏感[6]。

人体跌倒预测方法应具备两个要素：(1)准确性，必须能够有效区分跌倒过程和日常生活行为；(2)快速性，以便气囊在髋骨触地之前完全展开。为了预测跌倒行为，本文提出一种基于多变量时序关联分析的跌倒预测方法，通过实时获取人体驱干的三维角度和重力加速度，根据前倒、后倒和侧倒的时间序列，寻找合成角度与实时驱干倾角之间的关联性，可以有效区分在站立时发生前倒、后倒和侧倒；同时根据根据驱干倾角和合成重力加速度阈值，来决定是否启动跌倒触发，可以有效避免日常活动的误判。由于人体前向跌倒时可以通过肘部实现保护，而且弯腰的动作与前倒动作完全一致，本文只实现人体在发生后向跌倒和侧向跌倒的预测。

1 特征提取

1.1 特征部位的选择

运动过程中人体不同部位的加速度变化不同，为了提高跌倒识别的准确率，应选择不易于其他运动过程产生相似加速度和角度变化的部位作为信息获取的基准对象。腕部、手臂、腿部等部位因为在日常生活中改变频繁，具有很强的随机性，因而不适合作为特征提取部位[7]。而上躯干部位（髋关节以上、颈关节以下）在日常生活的行走、坐下、广播体操等活动中变化过程比较平缓，而在跌倒过程中姿态角度和加速度皆较为剧烈[8]，因此适合作为姿态和运动剧烈程度的特征提取部位，为了穿戴方便和不影响正常生活行为，选择特征提取部位为腰部。检测人体姿态和重力加速度的传感器选择整合了3轴陀螺仪和3轴加速度的InvenSense公司MPU6050芯片[9]，相较于多组件方案，免除了组合陀螺仪与加速器时之轴间差的问题，减少了安装空间，其自带的数字运动处理器DMP(Digital Motion Processor)硬件加速引擎，通过主IIC接口，向外部应用MCU输出完整的9轴融合演算数据，便于姿态解算，降低了运动处理运算对应用MCU的负荷[10]。

1.2 特征坐标系的建立

由于特征部位选取为腰部，则将人体的腰部作为坐标原点O。当出现跌倒运动时，姿态角与加速度会显著增加，因此，需要对加速度和姿态角建立特征坐标系。我们需要对人体各种运动下的加速度进行提取分析，为更好的观测加速度变化情况，对三个方向加速度分别进行分析，建立X，Y，Z三相坐标轴。为了方便姿态角之间的分析，采用MPU6050芯片对人体数据进行采集，其自带姿态角测量，其自身带有三方向坐标系，分别为Pitch角，Roll角，Yaw角。Pitch角表示人体与上下竖直方向之间的偏移角；Roll角表示人体与左右侧向水平方向的偏移角；Yaw表示人体前后水平方向的偏移角。最终建立如图1所示复合特征坐标系。

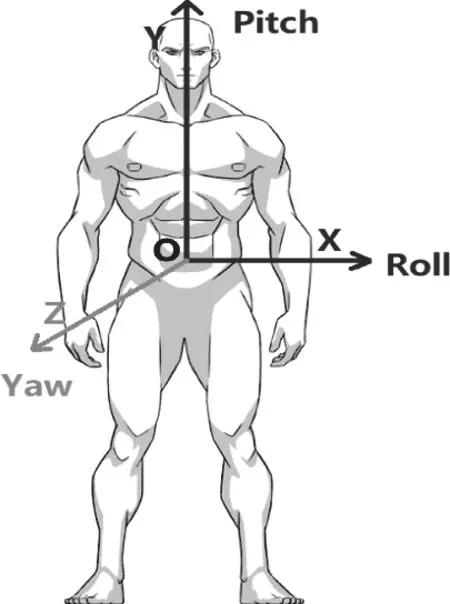
图1 坐标轴定义

2 多变量时序关联分析的跌倒预测算法

2.1 根据姿态角关联性区分

按照图1所示方向安装的陀螺仪，当直立时，Pitch角度接近90度，做前向、侧向弯腰和后仰动作时，Pitch角度变化范围是(0，90)度；在站立时，做向前弯腰和后仰动作时，Roll角度的变化范围是(-180，180)度；在站立状态做扭腰动作，Yaw角度的变化范围是(-180，180)度。为了区分日常生活行为和跌倒动作，需要根据姿态角对各种动作划分成三大类：第一类是向前弯腰动作，这是Pitch角度将会在(0，90)度间变化；第二类是左右侧向弯腰，这时腰部的Pitch变化角度在30度以内；第三类是站立时后仰动作，Pitch的角度变化量在30度以内。

通过图2发现，可以通过Pitch角度的变化幅度可以粗略的将动作分类两大类：前向弯腰和后向跌倒、正常行走侧向弯腰与后仰弯腰。为了进一步细分动作，需要将前向弯腰与后向跌倒动作进行区分，由于Roll角度在站立时，做向前弯腰和后仰动作时变化幅度是(-180，180)度，希望利用Pitch和Roll的合成角度与Pitch角度的关联性来进一步区分前向弯腰与后向跌倒，通过不断的实验，利用公式(1)的合成角度与Pitch角度的关联性可以有效的体现二者的区别。

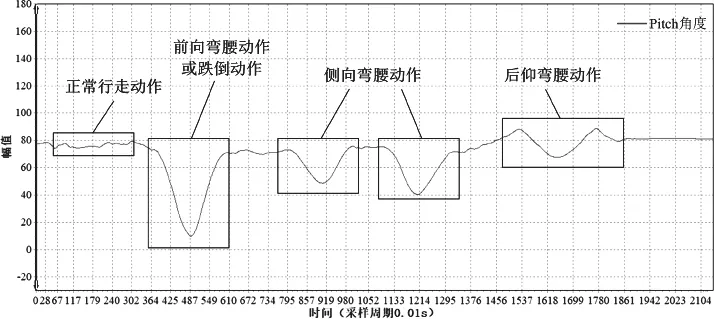
图2 各种动作下的Pitch角度波形

如图3所示为同步采集SqrtRP和Pitch角度的波形，按照公式(2)取SqrtRP和Pitch角度差值的绝对值RPP_delta，RPP_delta在各种动作下处在不同的区间，在正常行走和前向弯腰动作时，其值最小，也是需要过滤的动作；通过设置RPP_delta的阈值，可以有效的提取出侧向和后向的弯腰与跌倒动作。由于弯腰与跌倒动作，从姿态角度的变化是一致的，所有要提取正常的弯腰与跌倒姿态需要从他们的动作剧烈程度上进行区分，动作剧烈程度需要利用重力加速度进行判别。

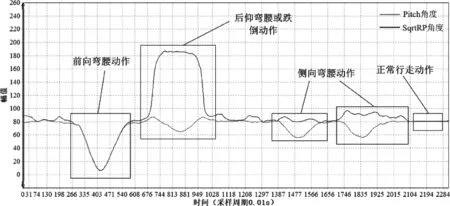
图3 各种动作下的SqrtRP和Pitch角度波形

2.2 根据重力加速度关联性区分

在人体从站立姿势到后向跌倒过程中，根据图1所示的坐标轴定义，其Z轴加速度可以体现此刻有无向后的剧烈运动、是否处于失重或与地面和座椅的剧烈撞击；同时在人体向后跌倒过程中，Y轴方向向下加速度也将有大幅度变化。因此，可以利用Z轴与Y轴加速度的幅值来区分后向跌倒与坐下后仰、坐下后躺和站立后仰等动作。为了利用Z轴与Y轴的合成加速度来建立在以上动作的关联性，定义Z轴与Y轴的合成加速度为SqrtAccYZ，其计算公式如下：

式中：AccY，AccZ——分别表示Y方向和Z方向加速度。

如图4-图6分别为站立后仰动作、坐下后仰动作、坐下后躺动作和向后跌倒动作的实时波形。

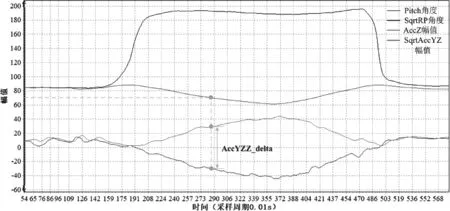
图4 后仰动作下的多变量波形

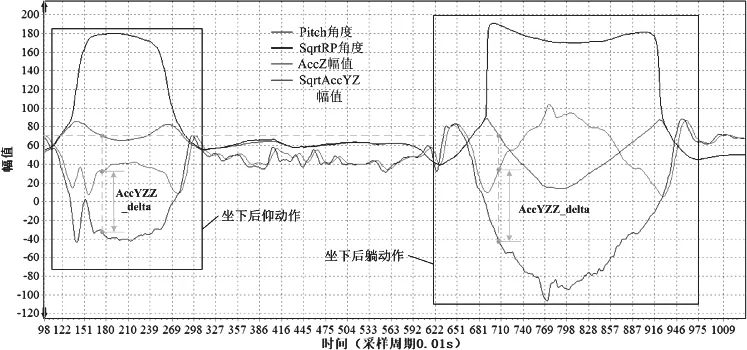
图5 坐下后仰和坐下后躺的多变量波形

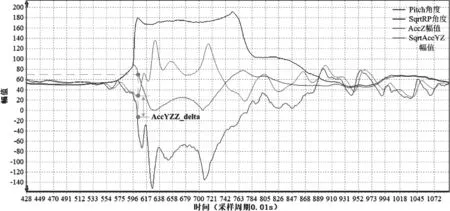
图6 向后跌倒的多变量波形

综合分析图4-图6之间的关系，发现当Pitch角度连续下降，并下降到跌倒预测的阈值70度后，通过观察AccZ与AccYZ的变化规律，定义AccYZZ_delta为AccZ与AccYZ的差值的绝对值，计算公式如式(4)所示，

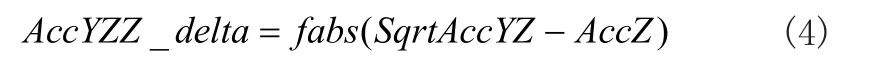
通过设置AccYZZ_delta的阈值，可以有效区分跌倒与站立后仰、坐下后仰和坐下后躺等动作。

2.3 算法的提出

经过之前对于多个数据变量进行关联性分析与整理，提出多变量时序关联分析的跌倒预测方法。首先通过姿态角阈值判别进行粗判别跌倒。在正常状况下，RPP_delta角度不超过30°，当出现弯腰或者跌倒动作时，RPP_delta角度超过30°。因此可以将RPP_delta阈值角度设立为30°，当阈值角度小于30°时，认为是人体正常活动状态；当阈值角度大于30°时进行下一步重力加速度关联性讨论判断。通过数据观察，可知当跌倒或者后仰时，Pitch角度会有下降的过程，当Pitch角度下降到阈值70°时，观察ACCYZZ_delta角度变化情况，发现后仰和后躺ACCYZZ_delta幅值为80左右，而出现跌倒动作时，ACCYZZ_delta幅值为40左右，因此可以设立阈值，进一步将后仰等正常动作与跌倒动作区分开。最终根据加速度，姿态角等多变量时序关联性分析的方法得到跌倒预测算法。跌倒预测算法流程图如图7所示。

图7 跌倒预测算法流程

3 算法验证

为了验证提出的跌倒预测算法的准确性和快速性，进行实验验证。实验验证选取数据为：RPP_delta阈值为70°，ACCYZZ_delta阈值为45。选择MPU6050为主芯片建立测试装置佩戴于测试者腰部，当出现跌倒动作是报警指示灯亮。测试者模拟正常行走、侧向弯腰、前向弯腰、后仰、后躺和跌倒动作各100次，记录预测结果以及报警指示灯亮响应时间。记录数据见表1和表2。

表1 各动作下测试准确率

表2 跌倒动作下响应时间达标率

由表1、表2，可知，跌倒预测准确率达到99.9%以上，满足准确性要求。响应时间小于0.1s的比例为96%，从站立到跌倒预测结果输出的响应时间在0.1秒内，而人体在发生跌倒时，整个跌倒过程为0.8秒左右，跌倒预测的判别时间为跌倒保护的触发预留了充足的时间，跌倒预测响应时间达标率为96%，满足了跌倒保护的快速性要求。因此，该跌倒预测算法满足准确性与快速性要求。