基于改进GOMP算法的OFDM稀疏信道估计

申蒙蒙，陈善恒，席纪江，杜钟祥

(1.中国矿业大学信息与控制工程学院，江苏徐州,221000；2.徐州市第一人民医院，江苏徐州，221000)

0 引言

在实际的无线通信系统中，收发端之间的信道通常十分复杂，各种噪声与衰落都是影响通信质量的重要因素，所以能够估计出信道状态信息对于无线通信系统十分重要，信道估计技术成为了衡量通信系统质量优劣的关键因素。信道估计即根据接收信号估算信道的状况，该估算过程与压缩感知里的重构流程十分相仿。MIMO-OFDM系统的大量研究表明，其信道符合稀疏特点，因此在信道估计环节结合压缩感知算法，能够在确保性能的同时，节省了大量的导频信息开销。

现如今，信道估计已取得大批研究成果，常见算法按照传输信号前是否加入用于先验的信号可分为三种。(1)在传输信号前加入一段信号用于辅助估计的训练序列，在接收端根据该序列计算待估参数被称作基于训练序列的算法。其中被大量运用的算法如最小二乘法以及线性最小均方误差法。(2)在传输信号前未使用训练序列做辅助计算的算法即盲估计方法，根据信号固有特征完成待估参数的计算，其中被大批使用的算法如子空间分析法和斜投影法运算复杂度较高，因而不适合大规模投入使用。半盲估计则是取上述两种信道估计算法的折中，即没有过于庞大的运算量，也没有过多的占用带宽，其中被广泛使用于无线通信系统的半盲估计算法包括基于少量导频信号反馈的半盲估计算法，以及利用子空间分析法结合信号固有特点进行估算的方法。都具有良好的信道估计性能。

伴随通信领域的发展，信道估计技术逐渐成为研究的热点和重点。最小二乘算法因为其较强的实时性在传统的信道估计算法里被广泛使用，但大量的导频信息成为传输信号的负担。在频谱利用率愈加重要的今天，减少传输导频信息产生的负担，成为现代通信领域的重要课题。压缩感知最早在2006年被提出，其主要内容是，具有稀疏特性的信号使用较少的采样值就可以较高概率地恢复原始信号，从此基于压缩感知的信道估计成为研究的新方向。文献[22]中，Raghavendra提出了经典贪婪算法(OMP)，完成了少量导频信号就可以恢复原始信号。OMP算法进一步发展为广义正交匹配追踪算法(GOMP)，通过在原子迭代过程中用选择选取相关性最大的S个原子代替原算法的一个原子，获得了更高的收敛速度。孙翠珍等人在时域使用曲线拟合将导频处的信道信息估计出来，极大的降低了算法的计算量。文献[24]提出了DCT信道估计算法，利用FPGA实验证明了该算法的信道估计性能。由此可得，在信道估计算法结合压缩感知完成待估参数的计算，能够在确保正确估计的条件下，减少频谱资源的消耗。

1 压缩感知理论

确保信号能够被高倍压缩率的条件是信号可以被稀疏表示，对信号x可做以下变换：

2 OFDM系统模型

2.1 OFDM通信系统基本模型

图1 OFDM的基本框图

在接收端，通过对OFDM信号做时间内的积分来恢复已调信号，假设解调第j个子载波，即对第j个子载波在T时间长度内积分来恢复已调信号，如式(8)所示。

其中0 ≤ i, j ≤ N−1

上文分别从时域和频域两方面描述了OFDM系统中子载波相互正交的特点，这使得解调时多个子载波不会互相混淆，也使得OFDM系统的调制与解调能够被快速傅里叶变换IFFT和FFT代替，极大的降低了计算复杂度。

2.2 OFDM系统稀疏信道估计模型

无线信道表现出稀疏性，结合压缩感知的理论模型可知，相关重构算法能较好地估计出来原始信道状态。OFDM系统子载波中选取P个传输导频符号，则接收端收到的导频信息可表示为：

通过式(12)和压缩感知理论模型对比分析可知，可将式中矩阵XP看做压缩感知中的观测矩阵，将矩阵WP看做压缩感知中的基矩阵，把矩阵A看做压缩感知中的感知矩阵。根据压缩感知重构算法计算出信道的时域响应值h,经过傅里叶变换后即为频域的信道冲激响应H。

3 改进OFDM系统信道估计算法

3.1 OMP算法

贪婪的压缩感知重构(OMP)算法因为其用法简单，易于实现等优点而被频繁使用。

OMP的执行步骤简单，易完成，所以OMP算法是一种经常被使用到的信道估计算法。OMP算法在每次迭代时利用信号残差与观测矩阵的每一列向量之间的内积值作为相关性的衡量，筛选出相关性最大的原子加入原子集，并通过最小二乘法计算信道估计值，继续迭代至满足停止条件，输出最终的估计值。

(6)迭代次数加一，并判断迭代是否终止，若未终止，则进入第(2)步，若迭代终止，则继续第(7)步。

3.2 GOMP算法

OMP算法进一步发展为GOMP算法，与之不同的是GOMP算法选取一个小于稀疏度的固定常数，记为S ，在原子筛选时，选择相关性最大的S 个原子，所以GOMP算法比OMP算法具有更快的收敛速度。当S=1时，GOMP算法即为OMP算法。GOMP算法的处理流程为：在每次迭代时用当前迭代时的残差与观测矩阵各个列向量之间的内积值来衡量相关性。选择相关性最大的S 个原子，并将其加入原子支撑集，并将其索引值加入索引集，利用最小二乘法估计此次迭代的信道估计值，然后更新残差。直到满足当前迭代时，残差的2-范数小于特定值ε，或者迭代次数满足t = min(K, M / S )，其中t=M / S 是使原子构成的矩阵满足列满秩。

3.3 改进GOMP算法

3.3.1 原子“弱”选择

在实际应用场景中，由于GOMP算法的条件为信号稀疏度已知，在实际中很难得到应用，受到原子“弱”选择方法[25]的启发，原子“弱”选择方法不是按照相关性选择原子，取而代之为设置一个阈值，将大于该阈值的原子组成原子集，抛弃其余原子，最后更新残差并迭代至满足迭代停止条件。

计算当前残差和恢复矩阵的内积值，然后将内积值中满足原子“弱选择”标准对应列元素放入原子集，并其列序号放入到索引集。原子“弱选择”方案使得该过程不受稀疏度K的限制，且可以按照当前残差和恢复矩阵的内积值调整选择原子的数目，有效避免预选过多和预选错误。提高了算法的稳定性。

3.3.2 DICE准则

通过以上分析可知，OMP算法以及GOMP算法通过内积值的方法来选择相关性较大的一个或S个原子，即分别计算当前残差与观测矩阵的各个列向量之间的内积值，用该值代表相关性。对于任意的两向量β以及λ，以下表达式即为内积准则的表达方法：

经典的基于压缩感知的信道估计算法常用内积准则来衡量向量之间的相似性。但用此方法代表相关性仍然有弊端，恢复信号时，观测矩阵中一些类似的原子对于信号残差的匹配存在影响，从而降低信号恢复的精度。

所以选择一种合适的度量方法用来筛选支撑集中原子，成为了影响信号重构算法优劣性的好坏的重点，所以本节根据此问题改进了度量准则，即在原子的第一筛选阶段使用Dice系数匹配准则。向量β以及λ之间的Dice系数匹配准则表达式为

对比分析内积准则与Dice系数匹配准则的数学表达式可知，内积准则表达式中分母的计算方法会破坏原有矢量的特点，所以内积准则难于区分类似原子，而Dice系数匹配准则的计算方法能够有效的解决该弊端。所以Dice准则能够筛选出更合适的原子，从而提高重构精度。

3.3.3 GOMP算法优化方案

为使得GOMP算法筛选出更优的原子，对其在以下两方面进行改进：

在原子筛选阶段，利用Dice准则取代传统的内积准则。并融合原子“弱选择”方式，在稀疏度未知时，在迭代时将大于该阈值的原子加入原子集，抛弃小于该阈值的原子。

该改进算法的执行流程为：

(1)首先给各个数值赋初始值：令迭代次数t=1，残差初始值r0=y，初始引集Λ0=φ，初始原子集A0=φ;

(2)将当前迭代时的残差与观测矩阵每个列向量按照Dice度量准则计算相关系数，将最大的I个值对应的列向量记为集合αJt2，其索引值构成集合Jt1；同时，将其中大于阈值Th =αmax{a bs( ut)}的值对应的列向量记为集合αJt2，其索引值记为集合Jt2。其中门限参数α的取值范围是[0,1)。

3.4 重构性能仿真分析

本小结实验通过MATLAB2014软件完成，为了验证改进算法的性能，在Matlab中进行了OFDM系统信道的仿真，采用误码率以及归一化相对误差作为指标，进行了GOMP以及改进GOMP算法的仿真。设置子载波数为256，循环前缀的长度为64，信道总路径数为256，多普勒频移默认为0。对步长s取值为3、6、9时，GOMP算法以及改进GOMP算法在不同信噪比时的信道估计性能进行仿真。仿真结果如图2及图3所示。

由图2可得，GOMP算法与改进GOMP算法在信噪比较小时的误码率较大，当信噪比增加时，误码率逐渐减小。且由图可得，误码率和步长成正比，步长越小，误码率越低。信噪比取40dB时，步长设置为3的GOMP算法误码率是0.8557×10-2，而改进的GOMP算法误码率为0.2356×10-2，由此证明改进的GOMP算法在误码率方面优于GOMP算法。

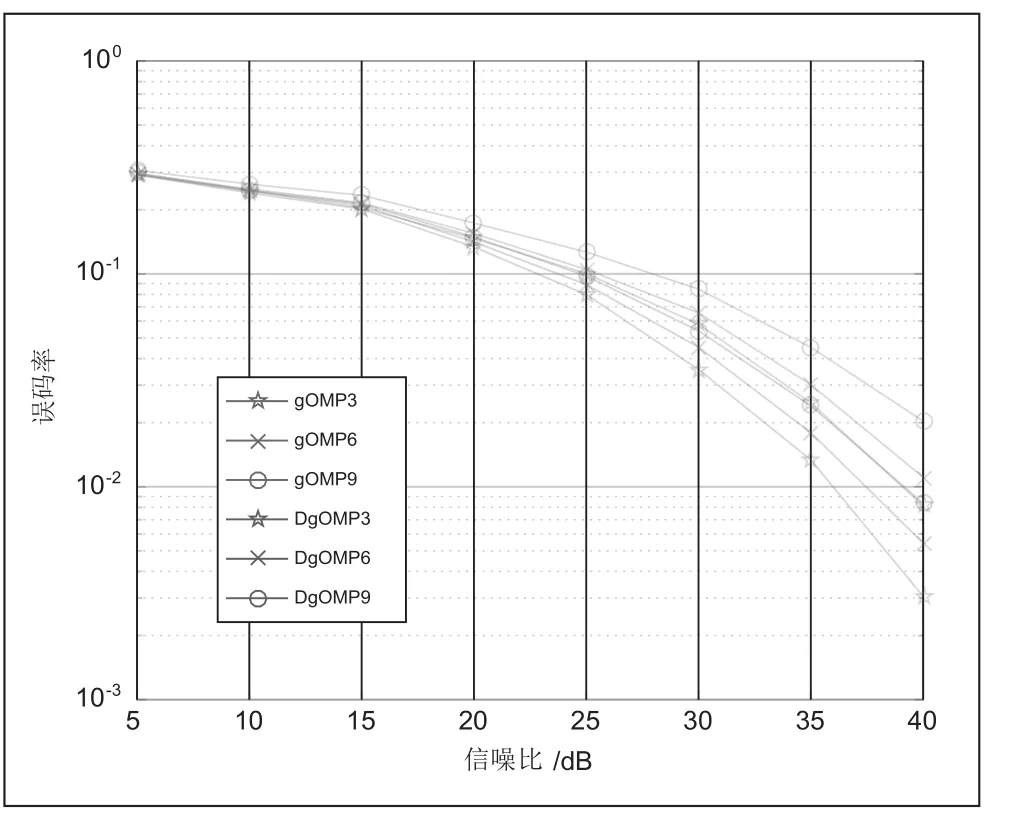
图2 改进算法与GOMP算法的误码率比较图

图3可以看出，归一化均方误差随着信噪比的增大而减少，当步长选择相同时，同一信噪比时改进算法比GOMP算法有更低的归一化均方误差。

图3 改进算法与GOMP算法的归一化均方误差比较图

4 小结

本文在OMP算法和GOMP算法基础上融合Dice准则筛选原子与原子的“弱选择方式”，极大改善了传统算法中内积准则无法从冗余字典中选取最优原子的弊端，提升了算法的稳定性。然后将此算法进行Matlab仿真实验，并与GOMP算法进行对比分析，仿真结果表明该算法简单易于实现，在信噪比一定时，改进算法的误码率与均方误差均有改善，可以有效提升信道估计性能。