设计数学美认知活动 培养高中生核心素养

黄桂福

（仙游第一中学，福建 仙游 351200）

美的追求不仅是艺术家的目标，也是数学家努力方向。数学中许多概念、公式、定理都充满了各种各样的美，有对称美、辩证美、统一美、结构美、简洁美等等。在数学教学中，要充分挖掘蕴含在知识发生发展过程中数学美的因素，精心设计数学美的认知活动，激起学生对美的追求，进而培养数学核心素养。笔者以全国卷近些年高考试题为例，就设计数学美认知活动，培养和发展学生的数学核心素养展开论述。

一、设计“对称美”认知活动，培养数学抽象、直观想象素养

对称美在数学中广泛存在，如几何图形中的轴对称、中心对称，代数中对称多项式、共轭复数等。教学中，对这些数学几何和代数知识适时引导，可让学生充分感知感受蕴含其中的对称美。

例1（2013 年高考新课标卷Ⅰ理科16 题）

若函数f(x)=(1-x2)(x2+ax+b)的图像关于直线x=-2 对称，则f(x)的最大值是______。

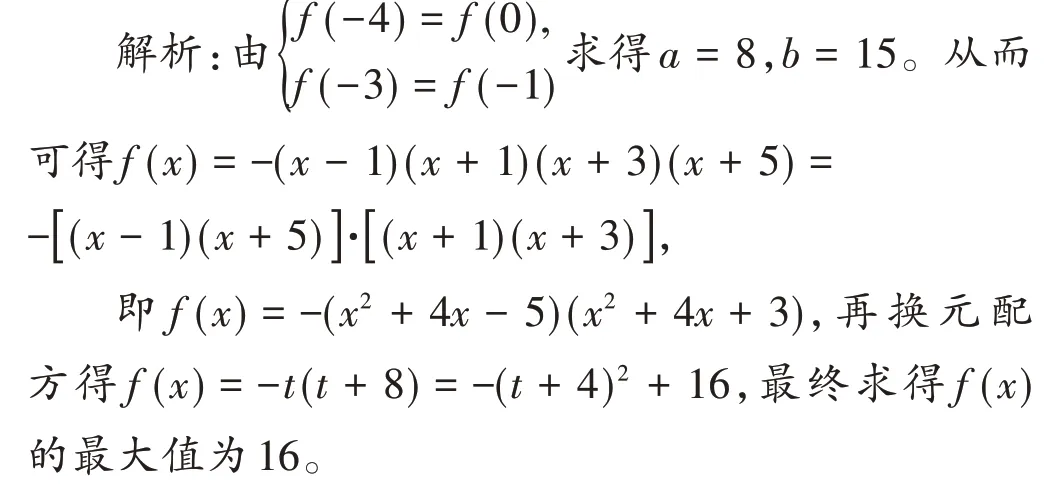
上述求解方法不仅繁琐，而且变形技巧太高，大多考生都无法顺利解答。

其实，若能基于数学的对称美和简洁美的角度，则问题可轻松获解，且几乎无运算量。为此，可做如下设计：

问题1：你能否从f(x)的关系式中获取有益的信息？

问题2：你能否基于对称性得到函数f(x)的关系式？

问题3：你能否基于简洁性对f(x)的最值作简化求解？

通过问题1，引领学生“从图形与图形关系中抽象出一般规律和结构”，即由函数f(x)的解析式可轻松抽象出f(x)有两个零点1，-1；

通过问题2，引领学生“借助位置关系、形态变化与运动规律”，即由f(x)的图像关于直线x=-2 对称，而f(x)有两个零点1 和-1，故f(x)另有两个零点-3和-5，从而得f(x)=-(x -1)(x+1)(x+3)(x+5)；

通过问题3，引领学生“利用图形描述、分析数学问题”，明了若将f(x)的图象右移两个单位，其最大值不会改变，于是可将求f(x)的最大值转化为求h(x)=-(x -3)(x -1)(x+1)(x+3) 的最大值，这样整个解题过程简洁明晰。

至此，直接配方即得h(x)=-(x2-5)2+16，故f(x)的最大值为16。

在上述活动中，学生既经历了“从图形与图形关系中抽象出一般规律和结构”，进而“借助位置关系，利用图形描述、分析数学问题”的对称美的认知过程，又从中使得数学抽象、直观想象等数学核心素养获得发展。

二、设计“辩证美”认知活动，培养逻辑推理、数学运算素养

数学中许多巧妙的证法，其思路往往借助各种辩证关系。因而，教学中设计“辩证美”认知活动，教会学生用辩证的眼光去观察、分析、解决问题，让学生经历数学逻辑推理论证中的辩证性与辩证美，可很好地培养学生的逻辑推理、数学运算等核心素养。

例2（2010 年高考新课标卷Ⅰ理科11 题）

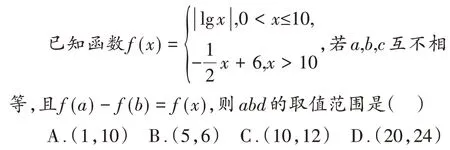
解析：本题直接求解难度较大，若利用数学的辩证美和奇异美，则问题瞬间获解，不亦乐乎。

为此，笔者进行如下设计：

问题1：变量a、b、c 的变化有规律吗？

问题2：这个变化是否具有一般性特征？

问题3：基于这个特征能否对问题作简化求解？

问题1 引领学生“从变化中抽象出一般规律和结构”，明了a,b,c 都是变量，且b、c 随着a 的变化而变化；问题2 引领学生“借助位置关系、形态变化与运动规律，利用图形描述、分析数学问题”，明了a 的变化具有一般性特征，即不论a 取何值，abc 的取值范围不变；问题3 引领学生“探究运算方向，选择运算方法”，明了若将a 特殊化，则可找出对应的b、c，验证选项即求解。

在上述活动中，学生既经历了“从变化中抽象出一般规律和结构”，进而“探究运算方向，选择运算方法”的“辩证美”的认知过程，也在推理论证中获得逻辑推理、数学运算等数学核心素养的发展。

三、设计“统一美”认知活动，培养数学抽象、逻辑推理素养

统一性是数学美的重要特征，如平面解析几何中圆、椭圆、双曲线、抛物线可统一在“到定点和定直线距离的比是常数的点的集合”这一定义之中。教学中，可设计“统一美”认知活动，以培养学生的数学抽象、逻辑推理等核心素养。

例3（2018 年高考全国卷Ⅰ理科第9 题）

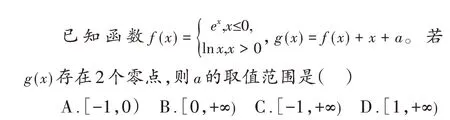
解析：本题若直接求解，需将“函数g(x)存在2 个零点”转换为“方程f(x)+x+a=0，即f(x)=-x -a存在两个实根”，所以“函数y=f(x)的图象与直线y=-x -a 有两个交点”。进而作出函数y=f(x)与直线y=-x -a 的图象以求解。

这样做过程繁杂，计算量大。其实，若能基于统一美、和谐美对函数g(x)的性质及图形作统一感知，问题可轻松获解，运算量也很小。

为此，教学中可设计为：

问题1：整体感知g(x)的解析式，它具有什么性质？

问题2：整体感知g(x)的图象，它的变化特征是什么吗？

问题3：能否基于函数性质与图形特征对问题作简化求解？

问题1 引领学生“从数量与数量关系中抽象出数学概念及概念之间的关系”，明了函数f(x)=具有统一性质：在(-∞,0)递增，在(0,+∞)上也递增；问题2 引领学生“从事物的具体背景中抽象出一般规律”，明了g(x)图象的变化特征：当x →-∞时g(x) →-∞，x →0 时g(x) →-∞，x →+∞时g(x) →+∞；问题3 引领学生“从条件和事实出发予以推理”，明了若g(x)存在2 个零点，必须g(0)≥0，从而由g(0)=1+a≥0，即得a≥-1，故正确答案为C，简单快捷，不亦乐乎。

在上述活动中，学生经历了“从数量与数量关系中抽象出数学概念及概念之间的关系”，进而“从条件和事实出发予以推理”的统一美的认知过程，也从中获得抽象、逻辑推理等核心素养的发展。

四、设计“结构美”认知活动，培养数学建模、直观想象素养

数学美还表现在结构上的统一上，例如，数学式子结构对称有序，数学元素的完备整齐等。教学中，应设计“结构美”认知活动，让学生感知感受蕴含在数学的结构性与结构美，可有效培养数学建模、直观想象等核心素养。

例4（2013 年高考全国卷Ⅰ文科16 题）

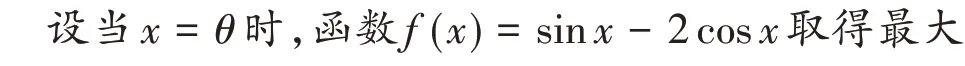
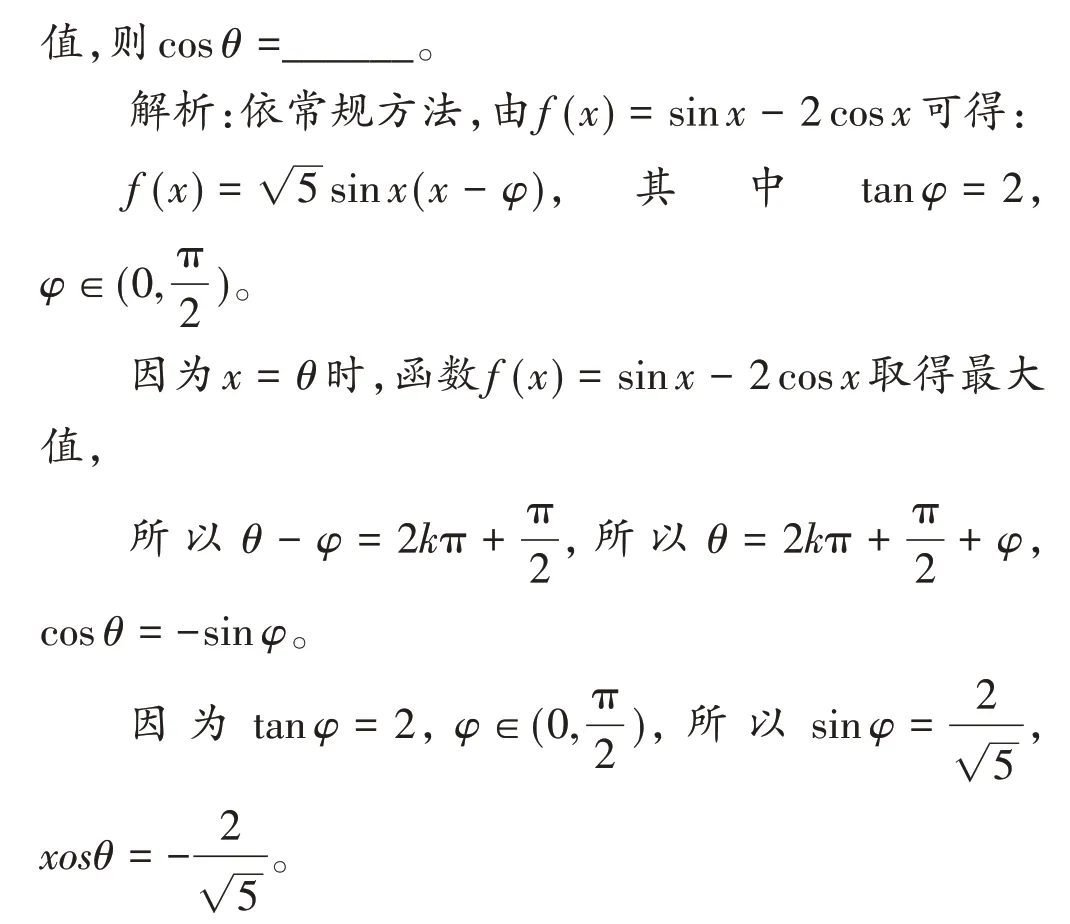
以上求解极为繁琐，费时费力，其实，若能基于直观美、结构美对函数g(x)的结构和性质作直观感知，问题可轻松获解，运算量也很小。

为此，教学中应设计“结构美、直观美”认知活动，这些活动过程包括：

问题1：你能识别出这个函数的模型和结构特点吗？

问题2：这个模型和结构的性质和特征是什么？

问题3：你是否可以借助这个性质和特征将问题简化求解？

通过问题1，引领学生“从数学的视角发现问题、提出问题，分析问题、构建模型”，明了这是形如y=a sin x+b cos x 的结构模型；

在上述活动中，学生经历了“利用图形描述问题，建立形与数的联系”的结构美的认知过程，以及从“从数学的视角分析问题、构建模型，验证结果并改进模型”，数学建模、直观想象等核心素养得到了很好的培养。

总之，教师在设计教学活动时，应通过具体的情境问题，架设数学美的认知桥梁，引发学生独立思考，进而让学生在不断感知“数学美”的过程中得到数学美的体验，获得数学核心素养的发展。