RHIC能区核碰撞中带电粒子的碰撞事例图研究

岳晓清，李保春

（山西大学 物理电子工程学院，山西 太原 030006）

0 引言

从最初的通过宇宙线实验来发现粒子，到现在世界上接连建起的高能加速器来进行高能粒子及其次级粒子的探测，都是为了全面地研究这些粒子的结构特征和在相互作用的基础上观察得到这些粒子的内在作用规律［1］。随着更高能量、更多种类粒子碰撞的实验不断发展创新以及对高能碰撞及其产生粒子的研究，我们将不断了解物质微观结构及其运动规律，并可以运用到其他尖端技术领域中。研究更内部、深处的物质结构时，就得有更精微的探针，粒子互相对撞的研究历史发展到现在，我们主要依托的是大型加速器：布鲁克海文国家实验室（Brookhaven National Laboratory，BNL）的相对论性重离子对撞机（Relativistic Heavy Ion Collider，RHIC）［2］和欧洲粒子物理实验室（European Organization for Nuclear Research，CERN）的大型强子对撞机（Large Hadron Collider，LHC）。主要的实验数据也出自这两个加速器上的多个探测器及其代表的合作组。本文中用于分析的实验数据正是来源于RHIC 上PHENIX 和PHBOBS 这两个探测器。

在重离子碰撞过程中，碰撞瞬时形成了温度极高密度极大的环境，夸克-胶子等离子体（QGP）物质短暂存在。在源静止系观察发现，末态粒子呈现各向同性散射的特征。但是，由于多个源之间的相互作用导致源的位置偏离了初始坐标轴，扩散也不再是球对称的。所以，实验观测到的是各向异性散射的末态粒子。最后得到的末态粒子是动力学冻结的结果。根据粒子的动量（和横向动量）、快度（和赝快度）等物理量，可以模拟出碰撞时粒子在不同空间中的散射示意图，即碰撞事例图。动力学冻结时刻的事例图可以直观展示碰撞后粒子动量、速度等分布及特点。不同空间的散点图可以帮助我们从多个角度理解高能碰撞下不同粒子的产生及其相互作用，用来分析和解释不同阶段粒子的性质和运动规律，并还原反应系统中一系列的碰撞过程。通过分析末态粒子在粒子束和垂直粒子束两个坐标轴上的散射谱，可以重现和模拟出可鉴别粒子在冻结时刻（即不再发生化学变化时）的情况。相应物理量是表征QGP 初始条件和随后动力学演化的重要观测结果，且在事例图中可以分析碰撞瞬间粒子动量、速度的分布和特点。所以，碰撞事例图给出粒子的出射分布结构，它的研究可以进一步解释高能碰撞中物质的演化机理及对末态的影响。

理论上，人们常采用一些统计方法来分析粒子产生，如：标准分布、厄兰分布、热柱模型和火球模型等。在热模型中，初始阶段的每个源出射粒子时不受其他源的干扰，并假设在源静止系中的出射粒子是各向同性的。由于领头粒子效应，反应体中领头粒子散射源可以视作独立发射源处理，而射弹旁观体蒸发源也可以视作独立发射源［3］。考虑到碰撞中有多个发射源，本文在热模型中提取到了有效温度的Tsallis 统计量［4］和平衡指标。改进后的热模型能够计算出碰撞过程的横向激发程度，可以计算出沿束流方向的快度、赝快度，结合有效量可以得到表征各物理量相互关系的碰撞事例图。

1 模型改进和计算方法

高能对撞中，定义对向的两束粒子分别为射弹核、靶核。当如此高的能量在反应体（领头粒子瞄准并发生碰撞的部分）中进行碰撞时，可以想象到射弹核和来自靶核的一部分会相互穿过，形成一段“柱体”，对应定义为射弹柱和靶柱［5］。此时观测的末态粒子可以视作来自多个源。假设在发射源静止，不同方向散射的末态粒子的性质均相同，此时其动量p′满足函数［6］：

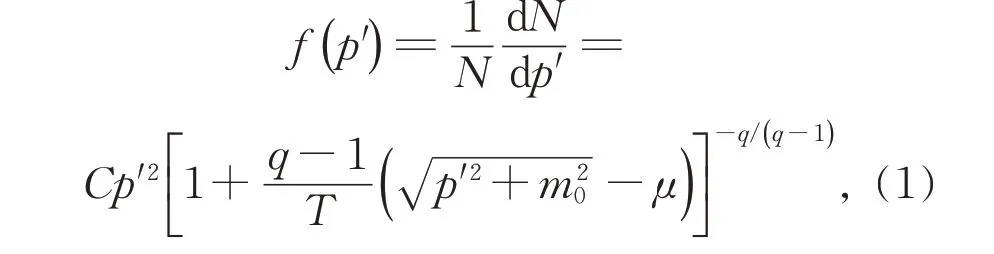
这里T表示发射源温度，q、m0和μ分别为热力学不平衡度（熵指数）、静止质量和化学势。本文研究的碰撞能量较大，因此可忽略化学势μ，此时公式（1）简化为：

又根据蒙特卡洛方法得到粒子在源静止系中的动量p′的分量p′x、p′y和p′z，有发射角θ′满足：

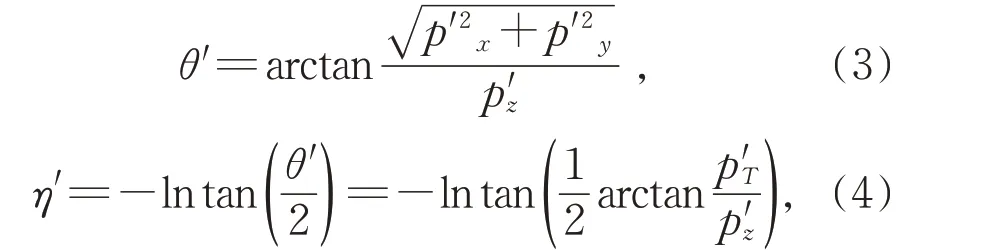
其中横向动量和纵向动量分别为：

和横动量函数：

考虑到质心系中碰撞包含射弹核、靶核和各自的领头粒子的影响，这一系列发射源的赝快度可以分别表示为：

其中yT、yP、yTmax、yTmin、yPmax、yPmin是快度分布参数，R1、R2是［0，1］区间里的随机变量。y和η在高能量时是近似的，重要的参考量是粒子动量的分量：

因为快度

所以可以在横向、x方向、y方向定义快度为：

通过公式（13）－（21）提取有效量，可以得到二维px－py－pz－pT、yT－y1－y2和βx－βy－βzβT的碰撞事例图。

2 结果与讨论

图1 在=200 GeV 能量下pp 碰撞中π0 的不变横截面与横向动量的关系Fig. 1 Invariant cross section of π0 as a function of transverse momentum in pp collisions at=200 GeV

图2 在=200 GeV 能量下pp 碰撞中h++h－的多源赝快度散射谱Fig. 2 Multiplicity dNch/dη of h++h－in pp inelastic collisions at=200 GeV

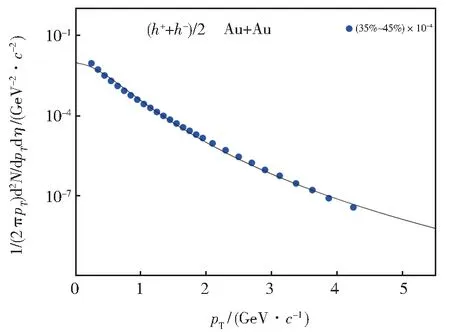
图3 在=200 GeV 能量下Au+Au 碰撞中h++h－的不变横截面与横向动量的关系Fig. 3 h++h－transverse momentum distribution in Au+Au collisions at=200 GeV

图4 在=200GeV 能量下Au+Au 碰撞中h++h－不同中心度的赝快度密度Fig. 4 h++h－multiplicity dNch/dη for different centrality bins in Au+Au collisions at=200 GeV

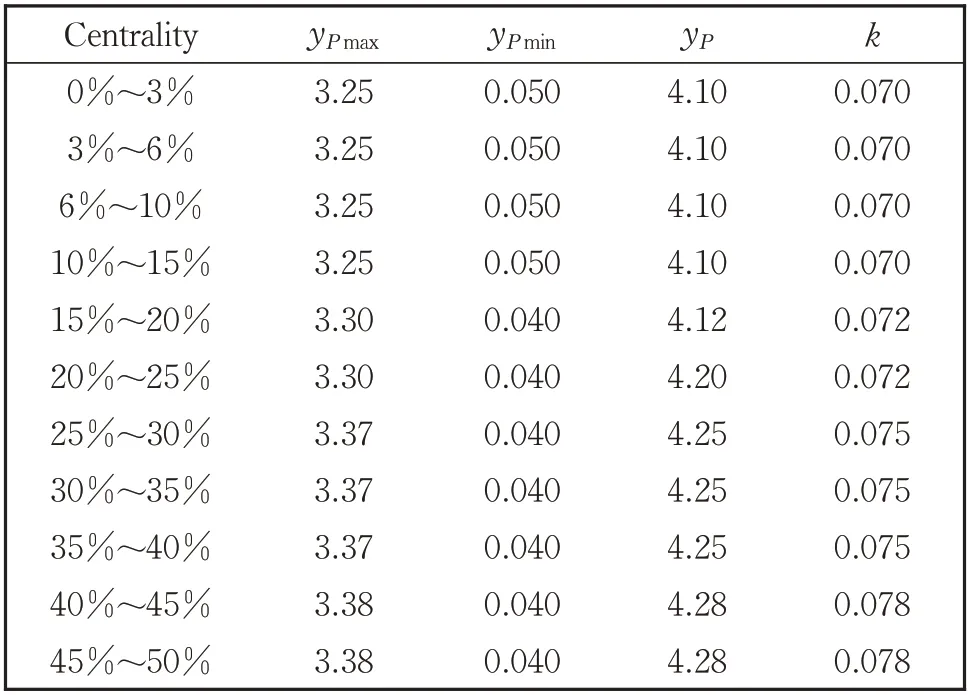
表1 图4中的模型参数Table 1 Parameter values corresponding to the solid curves in Fig.4

图1 和图3 是在相同能量下，不同类型粒子对撞产生粒子的横动量分布。因为碰撞核Au 比p质量更大，在两Au 碰撞中产生的横动量谱的分布更集中紧凑。这与pp碰撞相比其分布高度集中在数量级较高的区域，Au+Au 碰撞过程的横向激发水平更强，其发射源贡献的动力学膨胀程度也更大。这说明其横向压力梯度作用明显，横动量的散射分布较宽［10］。当碰撞产生的物质以较高的速度运动时，动量分布的洛伦兹效应明显出现，且与粒子质量成正比。两图中末态粒子分别为π0和h++h－，计算中的非平衡因子q均接近于1，这表明系统均接近于动力学平衡。图2 和图4 中赝快度分布呈现双峰结构，这是由于快度空间中靶柱和射弹柱部分重叠或分离导致的。另外，从图4 中可以看到赝快度分布随着中心度增大而增大，具有较强的中心度依赖性［11］。在Au+Au 碰撞最后的赝快度分布中，可以观察到中间赝快度区没有明显凹凸，pp碰撞的则有明显两个峰值。这表明小尺度的质子碰撞相较大的核-核碰撞，射弹核有较强贯穿能力，此时靶核的核阻止效应减小。两图对比发现粒子的赝快度散射分布的双峰凹陷与碰撞的核类型有关。

图5 =200 GeV 时pp 碰撞的动量空间事例图：（a）py－px；（b）px－pT；（c）px－pz；（d）pT－pzFig. 5 Momentum space event schematic of pp collisions at=200 GeV：（a）py－px；（b）px－pT；（c）px－pz；（d）pT－pz

由图可以观察到射弹柱和靶柱的表现。在动力学冻结时刻，各不同空间中的散射分布有重合部分。对比图5－7 与图8－10 的碰撞事例图，可以发现不同类型的粒子碰撞，产生的末态粒子散射在对应的空间中表现不同。对比图5 和图8 在px－pypz－pT空间的表现，Au+Au 碰撞后的粒子散射在束流方向有较大动量的分布。因核贯穿能力弱于pp碰撞，Au+Au 碰撞后在px－py空间的散射分布更近似于一个长条柱形，这反映了产生粒子在反应平面上的x方向被挤出时的流效，而pp碰撞在此空间表现为近似球状。对比图6 和图9，大部分末态粒子都有规律地分布在较小快度区域。在Au+Au对撞中的粒子在动力学冻结后，在快度空间的散射结果呈现比较疏松，而pp碰撞产生的粒子在快度空间的密度较大。图7 和图10 显示了速度空间中沿纵向方向集中了较多粒子，且在速度空间两种类型的粒子碰撞尺度相同。对比两图可观察到在pp碰撞中产生的粒子，在较大 ||βz区域散射分布会更集中。

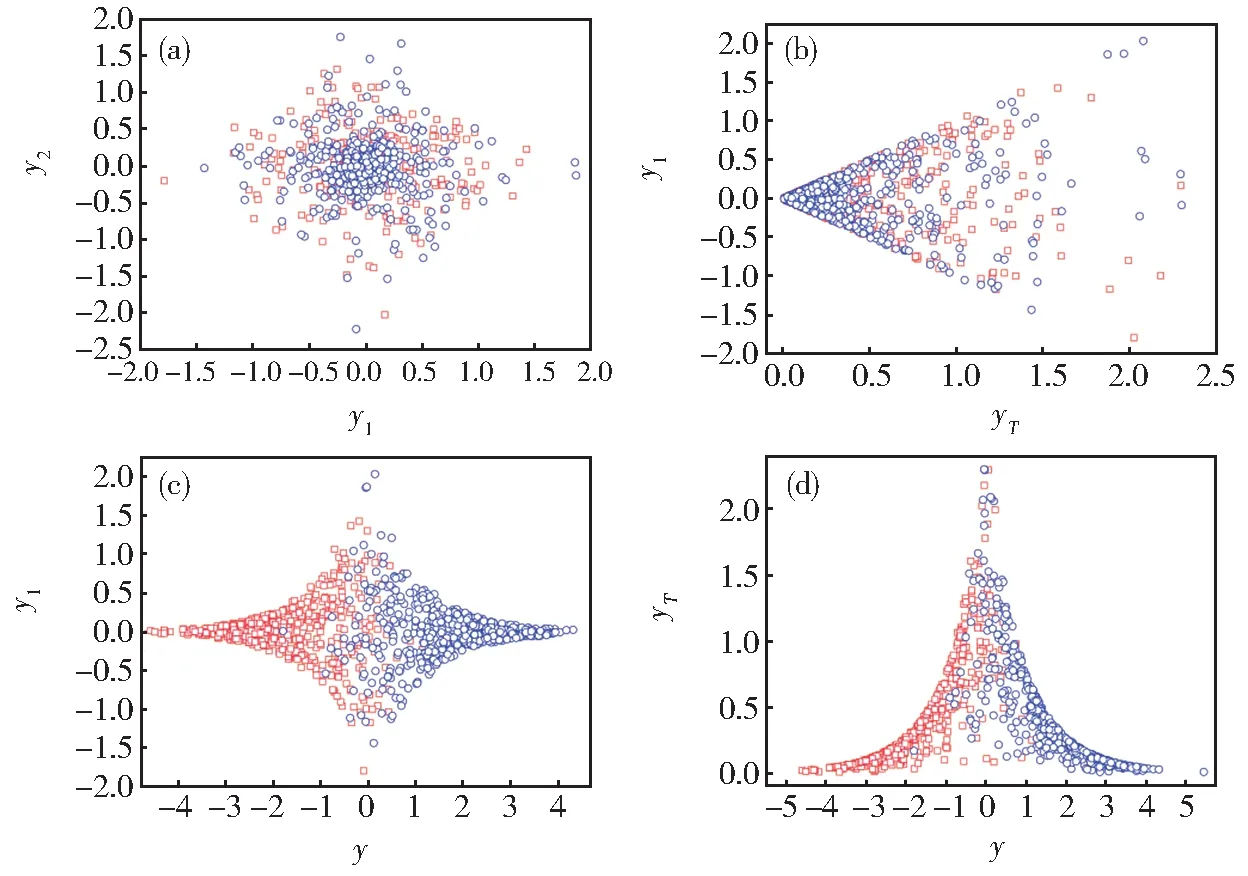
图6 与图5 相同碰撞的快度空间事例图：（a）y2－y1；（b）y1－yT；（c）y1－y；（d）yT－yFig. 6 Conditions are the same as those in Fig.5，showing an event schematic of the rapidity space：（a）y2－y1；（b）y1－yT；（c）y1－y；（d）yT－y

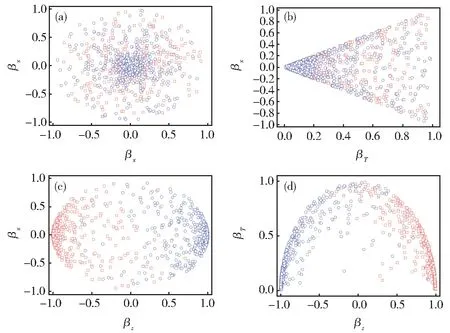
图7 与图5 相同碰撞的速度空间事例图：（a）βy－βx；（b）βx－βT；（c）βx－βz；（d）βT－βzFig. 7 Conditions are the same as those in Fig.5，showing an event schematic of the velocity space：（a）βy－βx；（b）βx－βT；（c）βx－βz；（d）βT－βz

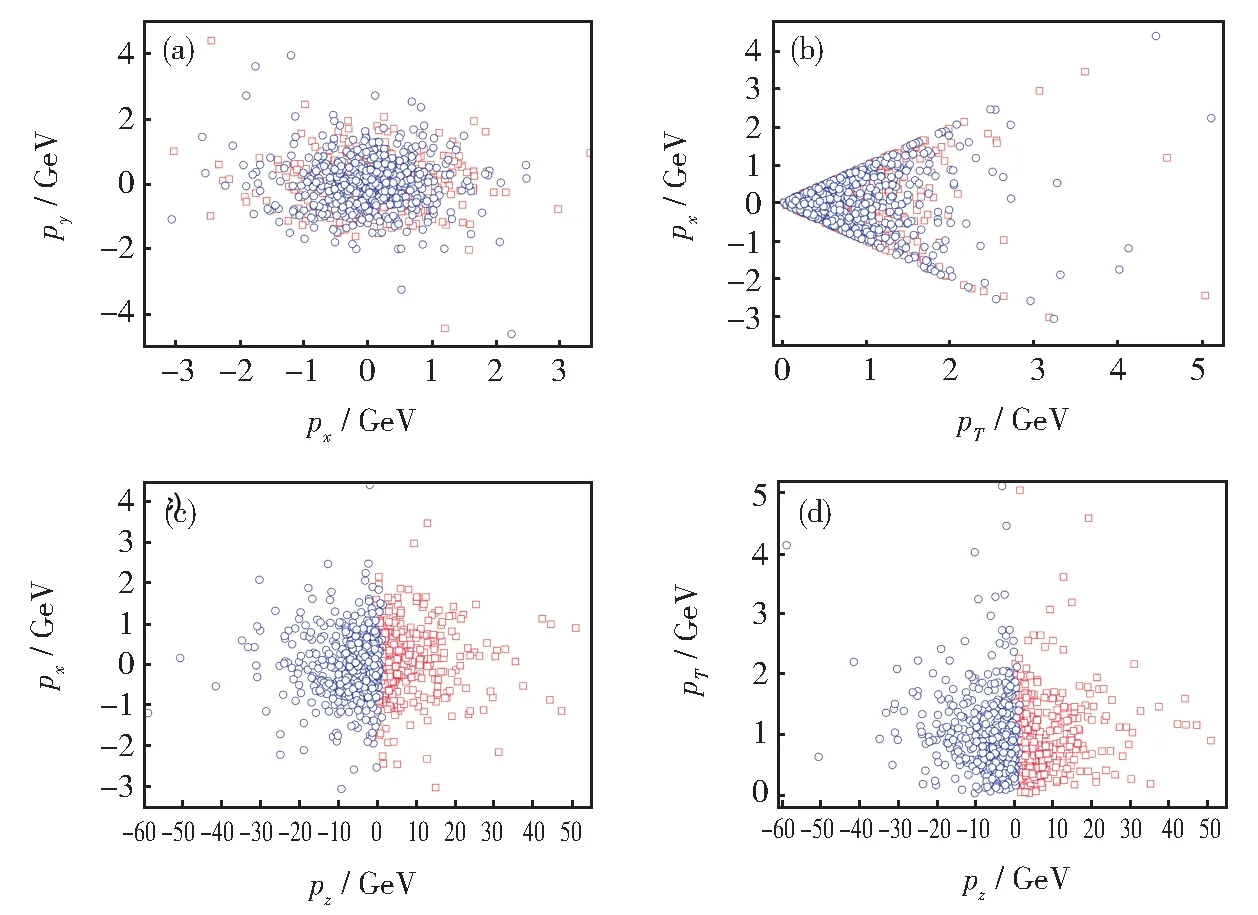
图8 =200 GeV 时Au+Au 碰撞的动量空间事例图：（a）py－px；（b）px－pT；（c）px－pz；（d）pT－pzFig. 8 Momentum space event schematic of Au+Au collisions at=200 GeV：（a）py－px；（b）px－pT；（c）px－pz；（d）pT－pz

图9 与图8 相同碰撞的快度空间事例图：（a）y2－y1；（b）y1－yT；（c）y1－y；（d）yT－yFig. 9 Conditions are the same as those in Fig.8，showing an event schematic of the rapidity space：（a）y2－y1；（b）y1－yT；（c）y1－y；（d）yT－y

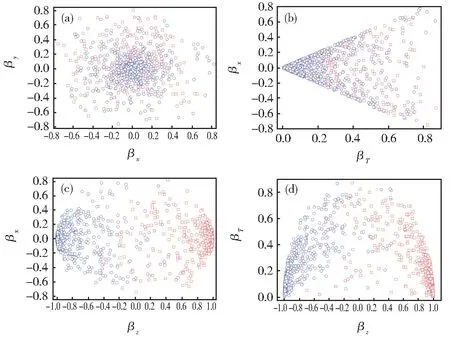
图10 与图8 相同碰撞的速度空间事例图：（a）βy－βx；（b）βx－βT；（c）βx－βz；（d）βT－βzFig. 10 Conditions are the same as those in Fig.8，showing an event schematic of the velocity space：（a）βy－βx；（b）βx－βT；（c）βx－βz；（d）βT－βz

3 结论

本文运用改进后的多源模型，结合末态粒子的散射分布的具体特征，计算了横动量和赝快度，研究了高能核碰撞不同空间中的粒子事例图，对实验结果进行了详细的分析。从研究中可以得出：在涉及质子的碰撞时，由于作用系统小，不需考虑或只需考虑一部分领头粒子的贡献，形成的热化柱也较其他碰撞要细，赝快度密度最高点较离子碰撞小了一个数量级。由于pp碰撞中靶柱和射弹柱重叠部分更少，pp碰撞产生的赝快度分布双峰图形中两峰与Au+Au 碰撞形成的双峰图相比更细，双峰中间凹陷明显。通过统计分析横动量谱和赝快度分布后，从中得到碰撞的具体参量，计算出了动量空间、快度空间和速度空间的粒子散射谱。在动量空间中，不同类型的粒子碰撞对散射分布的密度影响不同，且沿束流方向的动量分布范围较广。在快度空间，粒子散射会形成一个纺锤体，直观表现了快度的移动范围和相应区间的密度。在速度空间较大|βz|处，密度较大，并在这个方向上明显形成一个椭球形状。碰撞事例图在不同三种空间的表现证实了：高能核碰撞中产生的末态粒子可以从多个散射源的角度进行研究。