基于强度信息维数的加权网络分形特性分析

2021-08-31蓝文祥刘厚忠

南昌航空大学学报（自然科学版） 2021年2期

吴锋，张胜，蓝文祥，刘厚忠

（南昌航空大学信息工程学院，南昌 330063）

引言

复杂系统可以通过复杂网络来表示，复杂网络能对复杂系统进行较好的刻画和描述，一直受到人们的广泛关注[1]。复杂网络是研究复杂性的一种优秀的数学模型，被应用于各种学科领域[2]。研究复杂网络的拓扑特征对理解网络结构与网络动态行为之间的关系具有重要意义。1998 年和1999年两篇开创性的文章分别揭了复杂网络的小世界[3]和无标度特性[4]，这两个特性被认为是复杂网络的两个基本特性。随着复杂网络分形特性研究的兴起，源于分形几何的分形维数成为度量复杂网络的新研究热点，分形特性是复杂网络继小世界特性和无标度特性之后的第三大拓扑特性[1]。分形维数是衡量复杂网络分形特性最基本也是最重要的量，它常被看成是网络评价指标[5-7]。

2007 年，Song 等[8]基于盒子覆盖法提出了一种适用于复杂网络的贪心着色盒覆盖法，该算法将盒覆盖问题转换成了图论中点的着色问题，此算法因为简单且易于操作而被广泛应用于计算复杂网络的分形维数。Wei 等[9]考虑到覆盖盒子中节点数量上的差异提出了复杂网络信息维数法。Shanker等[10]最早提出了复杂网络体积维数法。受Shanker等的启发，Wei 等[11]考虑到节点度的信息，提出了复杂网络度体积维数法。Lacasa 等[12]提出了一种计算复杂网络关联维数的方法，该算法仅适用于坐标空间中的网络，Wang 等[13]将这一方法推广用于研究平面网络中的关联维数。上述方法都是针无权网络，对加权网络并不完全适用。受贪心着色盒覆盖法的启发，Wei 等[14]提出了适用于加权网络的盒子覆盖法(Box Covering Algorithm for Weighted Networks，BCANw)。黄等[15]受BCANw的启发，提出了加权网络体积维数法。Wen 等[2]受BCANw的启发，提出了加权网络信息维数法(Information Dimension Algorithm for Weighted Networks，IDANw)。受到BCANw和IDANw的启法，本文提出了一种分析加权网络分形特性的强度信息维数法。

1 加权网络常用统计量

1.1 节点强度

节点强度是加权网络中比较常用的统计量之一，对于一个给定的加权网络G，节点i的强度记为si，si定义如下：

其中wij是网络G中节点i和节点j之间边的权重值，Vi表示的是节点i的所有邻居节点组成的集合。节点强度和节点度的概念是密切相关的，实际上当wij≡1时，节点强度就退化成了节点的度。

1.2 边权

在加权网络中边权的定义有两种[16]：

1）相似权。边的权重值越大表示两节点间的相关性越强，节点间的距离也就越近。

2）相异权。相异权和相似权相反，边的权重值越大表示两节点的相关性越弱，节点间的距离就越远。

由于加权网络中边的权重有两种含义，从而导致节点间边权值的定义更为复杂。本文将节点i和节点j之间的距离记为dij，di j定义如下：

其中：i,h,k,l,j表示节点序号，wih表示节点i和节点h间连边的权重值。这里引入了参数q来区分相似权和相异权，q=1表明网络权重是相异权，q=−1表明网络权重是相似权。

2 基于节点强度的加权网络信息维数

2.1 算法思想

Wei 等[9]最早提出了BCANw，BCANw将网络中所有的边权值从小到大排序，对排序后的边权值从最小值开始不断累加得到盒子尺寸。Wen 等[2]受BCANw的启发，提出了一种适用于加权网络的信息维数法(IDANw)，IDANw只是简单的将无权网络中的信息维数法结合了BCANw中盒子尺寸的变换规则，该算法没有考虑加权网络本身的固有属性，依然是将盒子包含信息的概率定义为盒子中节点数与网络节点总数的比值。实际上，在加权网络中，节点间的连边有真实的含义。在IDANw的基础上，本文考虑到覆盖盒子中节点间连边的权重信息，重新定义盒子包含信息的概率，提出了一种分析加权网络分形特性的强度信息维数法(Strength Information Dimension Algorithm for Weighted Networks，SIDANw)。

实际上节点强度si包含了节点的度以及节点相连的边权wi j两方面的特征，是节点局部信息的一种综合表达方式。这说明用盒子中所有节点的强度和来衡量盒子包含信息的信息量是合理的。本文重新定义盒子i包含信息的概率记为pi，pi定义如下：

其中Hi表示盒子i中所有节点组成的集合，Sall表示在整个网络中所有节点的强度总和。根据式(4)以及香农信息熵的定义计算给定盒子尺寸r下网络的信息熵I(r)，I(r)如下：

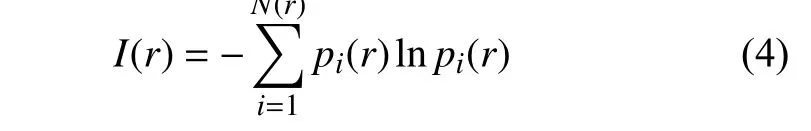
其中N(r)表示盒子尺寸r时覆盖网络所需的最小盒子数。综合式(3)和式(4)，计算复杂网络的强度信息维数ds，ds如下：

在计算实际网络强度信息维数的过程中，很难实现盒子尺寸r→0，通常做法是拟合I(r)与 lnr的关系，若呈线性关系，则直线斜率的绝对值就是网络的强度信息维数ds。

2.2 算法步骤

S IDANw算法详细步骤如下：

步骤1 给定加权网络G，将G中边的权重值按从小到大顺序排序，排序结果记为[l1,l2,···,ln]。

步骤2 求解网络G中任意两节点间的距离值di j，网络直径D=max(dij)，设置盒子的初始尺寸r=l1。

步骤3 给定盒子尺寸r，利用改进的贪心着色算法求解网络G的最小覆盖。

步骤4 对覆盖所得的盒子进行逐一编号，由式(4)计算盒子i包含信息的概率pi(r)，基于这组概率值，根据式(5)计算出盒子尺寸r下网络G的信息熵I(r)。

步骤5 分别设置盒子尺寸r=l1+l2,r=l1+l2+l3,r=l1+l2+l3+l4+···，重复步骤3 和步骤4，直到盒子尺寸r≥D，记录每个盒子尺寸r对应的信息熵I(r)。

步骤6 在直角坐标系中刻画出 ln(r)与I(r)对应的数据点，通过最小二乘法拟合实验数据，若存在线性关系，表明G具有分形特性，直线斜率的绝对值就是网络G的强度信息维数ds。

实际上，步骤3 中改进的贪心着色算法是针对加权网络中BCANw的改进算法，该算法推广了无权网络中改进的贪心着色算法的思路，在无权网络中，节点的着色过程主要是考虑到了对偶网络中节点度的信息，对于孤立节点，选择与对偶网络中节点度最大的节点相同的颜色。而在加权网络中，本文考虑网络中每个节点的强度属性，将对偶网络中的节点按照节点强度的大小顺序进行编号，节点强度大的节点优先编号，着色过程中按照编号顺序依次着色，对于孤立节点，选择与网络中节点强度最大节点相同的颜色，这种做法同样可以降低算法的随机性，从而让算法运行结果更加稳定。

3 实验结果及分析

为了验证本文算法的合理性以及可靠性，本文用S IDANw分析两类构造加权网络的分形特性，以及在三个真实加权网络中与IDANw和BCANw算法做对比实验。

3.1 分析构造加权网络的分形特性

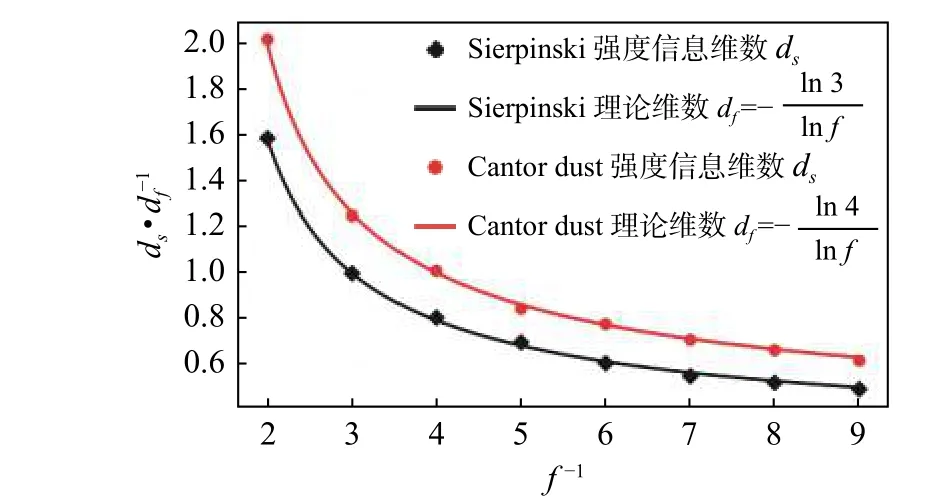
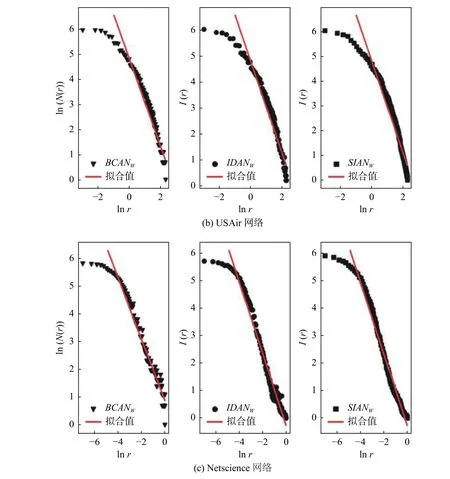
加权分形网络的概念是Carletti 等[17]首次提出的，实际构造加权分形网络的过程主要是利用迭代函数系统。构造的加权分形网络的豪斯多夫维数由两个参数共同决定，一个是复制数s，另一个是比例因子f，其中s，f分别满足s>0, 0

对于Cantor Dust 加权分形网络，这里将图形复制数目s设置为4，第六代Cantor Dust 加权分形网络G6包含的节点数为13 653。这里选用G6做实验，具体的实验步骤和Sierpinski 加权分形网络类似，最终实验结果如图1b 所示。

图1a 和图1b 中横坐标表示盒子尺寸的对数值，纵坐标表示的是给定盒子尺寸下的信息熵。从图1 可以看出，无论是Sierpinski 还是Cantor Dust加权分形网络，本文算法在不同的比例因子f下，盒子尺寸的对数值与信息熵呈现很好的线性关系。

图1 不同f 值下Sierpinski 和Cantor Dust 加权网络的分形特性分析

当s=3时，给定f的值，Sierpinski 网络的理论分形维数值可由式(6)计算：

当s=4时，给定f的值，Cantor Dust 网络的理论分形维数值可由式(6)计算：

图1 拟合所得的强度信息维数ds以及由式(7)和式(8)所求的Sierpinski 和Cantor Dust 加权网络的理论维数df如表1 和表2 所示。

表1 s =3， Sierpinski 不同 f 值对应的强度信息维数与理论维数

表2 s =4， Cantor Dust 不同 f 值对应的强度信息维数与理论维数

为了更加直观看到本文算法的实验效果，图2给出了不同f值下两类构造网络的理论维数曲线和实际计算的强度信息维数。

图2 Sierpinski 和Cantor Dust 在不同 f 值下的理论曲线和强度信息维数

表1 和表2 以及图2 可看出，对于Sierpinski和Cantor Dust 加权分形网络，当给定比例因子f的值时，S IDANw计算出的强度信息维数与网络的理论维数十分接近，这表明本文算法可以很好地度量构造加权网络的分形特性。

3.2 对实际加权网络的分形分析

为进一步验证本文算法的合理性，本文选择了3 个真实的加权网络来做实验。3 个真实网络分别是Lemis 演员合作网络，USAir 美国航空网络以及Netscience 科学家合作网络。演员合作网络包含77 个节点和254 条边。科学家合作网络包含1589 个节点和2742 条边。美国航空网络包含332 个节点和2126 条边。

为了更加直观的看到实验效果，将S IDANw与BCANw和IDANw算法所得的结果进行对比。以上3 个实际网络在不同算法下的拟合效果如图3a～图3c 所示。

BCANw，IDANw和S IDANw计算所得的分形维数分别记为db，di，ds，计算结果如表3。

BCANw，IDANw和S IDANw计算所得的均方误差分别记为Qb，Qi，Qs，计算结果如表4。

从表3 可以看出BCANw，IDANw以及S IDANw所求解出的维数很接近。对于演员合作网络，分别为1.169，1.148 和1.185。对于美国航空网络，分别为1.174，1.182 和1.168。对于科学家合作网络，分别为1.763，1.778 和1.784。从图3 和表4 可知这3 个算法都能度量这3 个实际加权网络的分形特性，但是本文算法的拟合误差和拟合效果比IDANw和BCANw更优。