自动驾驶汽车乘员个性化乘坐舒适性辨识方法*

2021-08-31兰凤崇李诗成陈吉清沈宗卯

汽车工程 2021年8期

兰凤崇，李诗成，陈吉清，沈宗卯

（1.华南理工大学机械与汽车工程学院，广州510640；2.广州小鹏自动驾驶科技有限公司，广州510640）

前言

自动驾驶汽车是集环境感知、智能规划决策、跟踪控制等为一体的复杂系统［1-2］。随着车辆智能化程度不断提高，车辆环境感知传感器识别精度不断提升，离自动驾驶的终极目标越来越近，若把环境识别当成人的眼睛，智能规划决策则是人的大脑，如何规划既满足安全舒适又满足个性化需求的轨迹，是目前亟需解决的问题。

自动驾驶车辆的路径规划/轨迹规划方法主要有线插值方法、采样方法、机器学习方法和最优控制方法等［3-7］，这些轨迹规划方法根据环境感知信息和车辆自身状态判断车辆所处的场景，根据不同的驾驶场景构建安全无碰撞行驶轨迹，其约束条件主要为轨迹曲率、与其他交通车安全距离、通行时间和加速度等，规划的轨迹需满足车辆的安全性、舒适性和通行效率等要求。部分学者以规划过程中加速度变化率来表征车辆乘坐舒适性，以此来构造兼顾舒适性和安全性的最优控制轨迹规划算法［8-9］，但是此方法缺乏对乘员个性化需求的考虑。多样化的规划和控制方法带来了不同的自动驾驶汽车乘坐体验，为满足个性化驾驶要求，一些研究从驾驶员驾驶习性入手，对驾驶风格进行聚类分析，以安全约束和驾驶风格为条件，搭建考虑驾驶风格的自动驾驶汽车换道轨迹规划算法［10-12］。随着驾驶员逐步被替代，自动驾驶汽车的个性化和多样性最终将面向乘员，传统的平顺性评价方法更注重不同路谱和乘员座位材料等因素在振动下对乘员舒适性的影响［13-14］，但此种评价存在滞后，无法实时对自动驾驶汽车规划和控制质量做出全面的评价。故须搭建评价自动驾驶汽车轨迹规划乘员舒适性的算法，辨识行驶参数与乘员舒适性的关系，为考虑乘员个性化舒适性轨迹规划算法的搭建做铺垫。

1 乘员乘坐舒适性辨识方法

1.1 乘员乘坐舒适性评价

车辆自动驾驶是横纵向规划控制耦合的过程，控制参数直接影响乘员乘坐舒适性，不同乘员对于振动的反应不同，评价指标主要包括转向修正时主车横摆特性、转向修正中车辆侧倾表现、转向修正末期车辆横摆收敛、转向修正（频繁）超调现象、转向盘摆振现象、系统转向修正强度、纵向加速度柔和度等，可以通过主观感觉和客观测量两个方面评价。

1.1.1 主观感觉评价

对比SAE主观评价标准［15］，根据自动驾驶规划控制系统的差异，按行驶过程分阶段对舒适性进行评价，以换道过程为例对初始、中间和结束3个阶段与换道整体舒适性进行评价打分，制定乘员主观感受评价方式，见表1。

表1 驾驶员驾驶主观舒适性评价方法

1.1.2 客观时域频域评价

标准ISO2631—1：1997根据座椅支撑面xs、ys、zs三方向振动时域和频域加权均方根评判乘员乘坐舒适性。

（1）频域加权

对各向加速度时间历程a(t)进行频谱分析得到功率谱密度函数Ga(f)，频谱离散值为式中N为傅里叶变换点数，则

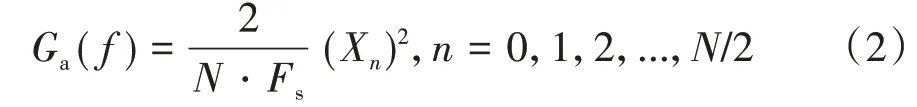
式中Fs为采样频率。

进而各轴加权均方根为

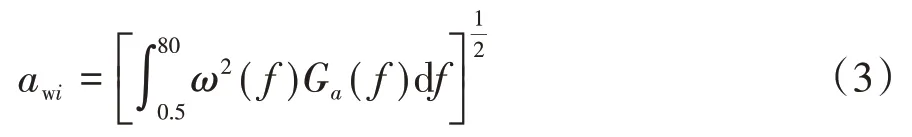
式中ω(f)为加权函数，其在xs、ys方向为wd(f)，在zs方向为wk(f)，在0.5~80 Hz频率范围有

总的加权加速度均方根值为

式中ki为各方向加权系数，在xs、ys方向为1.4，在zs方向为1。

（2）时域加权

规划评价往往持续时间较短，采样点较少，存在频域分析的频谱估计误差和噪声较大的问题，为确保客观舒适性数据的准确性，对此加速度进行时域分析。

当峰值系数aw（t）的峰值与aw的比值大于9时，认为车辆舒适性较差；当其小于9时，设计频率加权滤波器获取加权加速度时间历程aw（t），对采集的a(t)进行加权滤波，基于IIR无限长冲激响应滤波器理论［16-17］，得到加权加速度时间历程aw（t），再对各轴aw（t）进行积分得到均方根值：

1.2 考虑乘员舒适性的轨迹规划辨识方法

自动驾驶规划控制参数最后作用于车辆输出行驶参数，当前轨迹规划过程主要考虑横纵向位置和加速度指标，忽略了垂向加速度和不同乘员在不同轨迹规划控制下的乘坐感受。为了满足自动驾驶车辆乘员乘坐舒适性，提出一种考虑乘员舒适性的轨迹规划方案（见图1），综合考虑乘员主客观舒适性评价指标、轨迹规划车辆状态参数、操作参数和环境场景参数，搭建系统规划控制参数和乘员舒适性的辨识模型，进而生成满足不同乘员个性化乘坐需求的最优轨迹。

图1 考虑乘员舒适性的轨迹规划辨识方案

2 舒适性评价数据采集

2.1 数据采集平台和参数标定

2.1.1 数据采集平台搭建

为了采集自然驾驶过程中车辆行驶状态舒适性评价参数，搭建了实车试验参数采集平台，如图2所示。

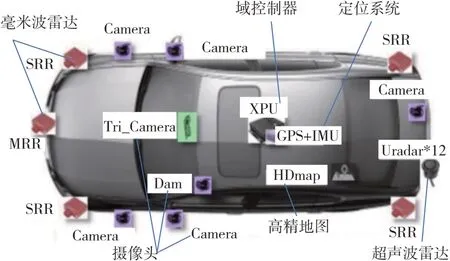
图2 数据采集平台

通过摄像头识别分类环境目标、毫米波雷达获取周围目标运动和位置信息、定位系统和高精地图获取自动驾驶车辆当前位置和运动等信息，域控制器接收并处理传感器信息，并传入下层决策控制模块；此外数采系统包括CANape、NOVATEL、Linux工控机、数据处理电脑等设备，可采集车辆位置信息、转向盘转角、电门、制动踏板、车速，纵向和侧向加速度，横摆、侧倾、俯仰角加速度等车辆行驶状态信息。

2.1.2 舒适性采集参数标定

高级别自动驾驶主要采用视觉和激光雷达+高精地图方案，根据车道线和行驶环境生成参考行驶轨迹，基于局部环境信息生成一条车道保持或换道超车的局部规划行驶轨迹，自动驾驶系统对车辆速度和跟车距离进行控制，使车辆保持车道行驶。当遇到前方慢车或车辆行驶路径与车道功能不匹配时，车辆执行换道超车动作，不同乘员对于车辆的驾驶风格和乘坐舒适度要求不同。

自动驾驶系统主要操控电门、制动踏板和转向盘，对应输出为横纵向行驶参数。基于车辆平台通信架构，对车辆输入和输出参数进行标定和校正。

对电门踏板、制动踏板行程（mm）、俯仰角（（°））和纵向加速度（m/s2）进行标定；其中电门踏板为电门行程占电门总行程的百分比，又称电门开度（如20%）。分析各参数变化规律，将电门踏板开度缩小10倍，制动踏板行程缩小5倍并取反，进行类归一化得图3。

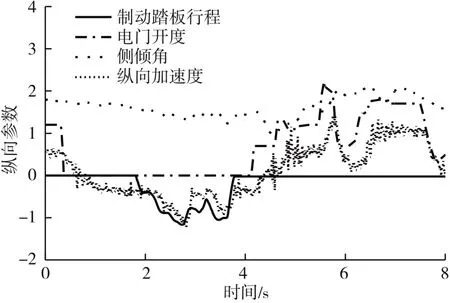
图3 纵向参数标定

对转向盘转角（（°））、横摆角加速度（（°）/s）、侧倾角（（°））和侧向加速度（m/s2）进行标定；将转向盘转角缩小10倍，横摆角加速度缩小3倍并取反，进行类归一化得图4。

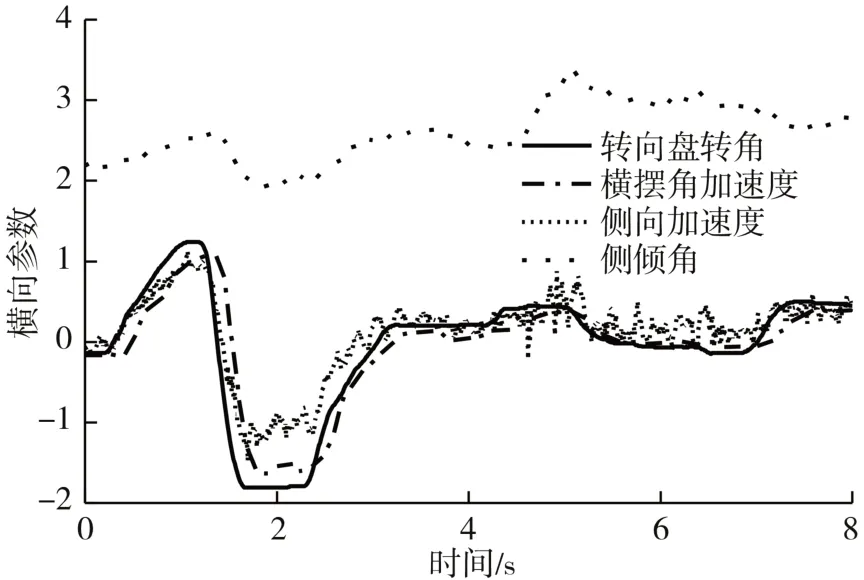
图4 横向参数标定

电门踏板开度、制动踏板行程、俯仰角与纵向加速度正相关，转向盘转角、横摆角加速度、侧倾角与侧向加速度正相关，加速度响应及时，滞后较小。

随机选取10组加速度信号进行处理得到时频域加权方均根，见表2。两种方法的运算误差较小，根据轨迹规划中车辆操纵稳定性对舒适性影响［18］和舒适性参数采集标定车辆参数变化规律，采用侧向车辆加速度变化率、三轴向加速度大小等过程特征参数来评价乘员舒适性。

表2 频域时域加速度加权均方根

2.2 舒适性影响参数采集

2.2.1 舒适性数据采集

道路激励和驾驶员或自动驾驶系统的操作均影响乘坐舒适性，换道超车基于车道保持实现不同车道的切换，是乘坐舒适性评价的典型场景，故以换道超车对舒适性影响参数进行采集。

招募5年无事故的驾驶员，采集车配备记录员和乘员。在高速公路高精度地图下，设置导航到目的地，数采设备开始记录数据，基于导航指引沿高速公路行驶，当驾驶员换道超车时，记录换道时间点和乘员主观舒适性。为提升样本的丰富性，1名乘员最少体验5辆数据采集车，每辆车换道体验不少于15次。自然驾驶数据包含车辆位置（经度、纬度和高度），纵向、侧向、垂向加速度，转向盘转角，转向盘转角速度，横摆角速度，横纵向车速，制动主缸压力，电门开度，质心侧偏角，航向角，俯仰角，侧倾角，换道时与前车的相对距离，相对速度等数据，乘员主观舒适度和座椅支撑面三轴向加速度等。例如，加速度、换道时车速与前车距离的变化如图5和图6所示。

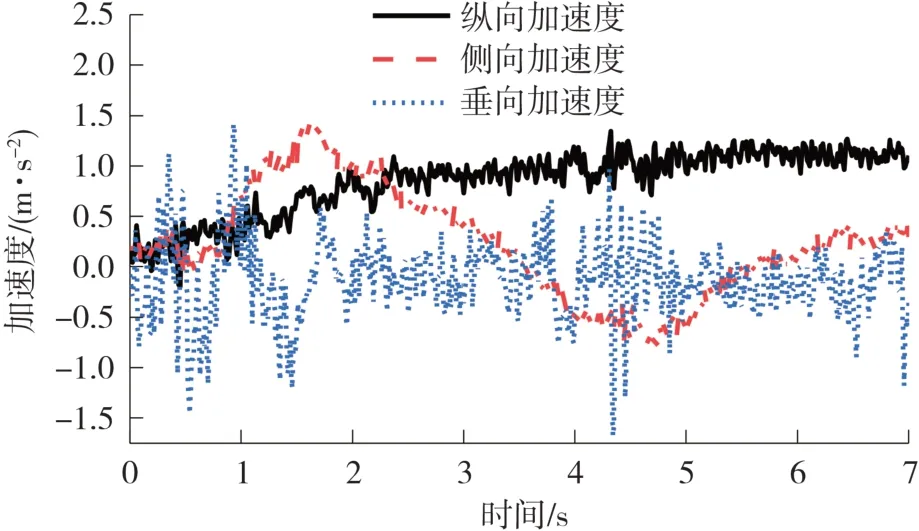
图5 横纵向和垂向加速度

图6 换道速度与前车距离

2.2.2 换道评价数据获取

以记录时间点切割前后10 s数据（见图7），基于转向盘转角和位置变化信息确定车辆换道过程初始和结束时间点。

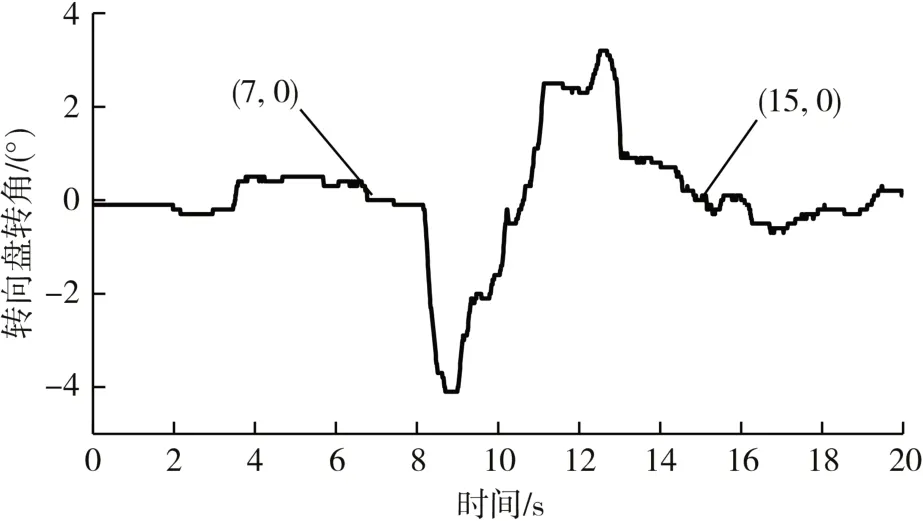
图7 转向盘转角变化信息

利用经纬度计算车辆位置变化，先将LLA坐标（lon，lat，alt）转化为ECEF下的地心坐标（X，Y，Z）

其中：e=

式中：a、b分别为地球长短半径，取值6 378 160和635 677 m；e为第一偏心率；N为椭球体的曲率半径。

以换道起点ECEF坐标为原点（X0，Y0，Z0），LLA坐标原点为（lon0，lat0，alt0），计算得到换道轨迹ENU坐标，以换道原点车头航向（θ）为X1轴正方向进行坐标转换，得到换道局部轨迹坐标（X1，Y1，Z1）：

式中S为ECEF坐标到ENU坐标系的坐标变换矩阵：

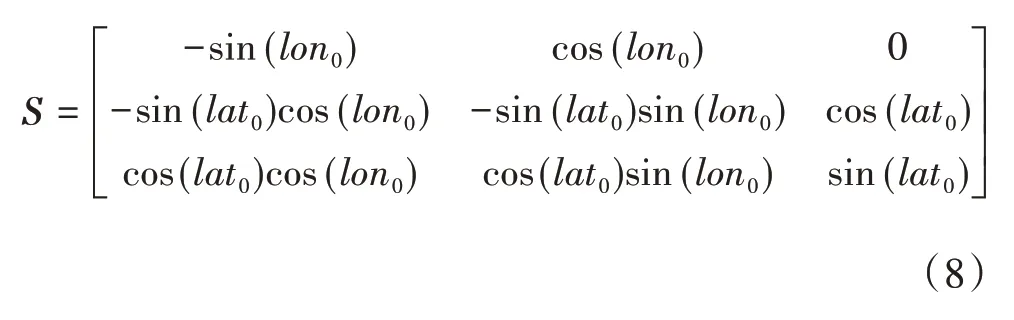
图8 车辆换道轨迹

2.2.3 换道舒适性参数提取

对换道初始、中间和结束过程分数取均值，得到最不舒适阶段和整体舒适度评价情况，乘员舒适性主客观参数包括换道整体舒适度分数、换道过程舒适度分数均值、换道过程最不舒适最大值、换道时域和频域加权方均根共5个参数。

为辨识自动驾驶汽车轨迹规划约束参数与舒适性参数的关系，随机获取300组数据。基于标定数据相关性分析对参数进行降维，以换道侧向加速度代表侧向输入输出指标（转向盘转角、横摆角加速度、侧倾角）；以纵向加速度代表纵向输入输出指标（电门踏板开度、制动踏板行程、俯仰角）。为了充分反映过程参数变化特征，横、纵、垂向参数取最大值、均值，其中横向加速度变化加入标准差，最终得到参数如表3。

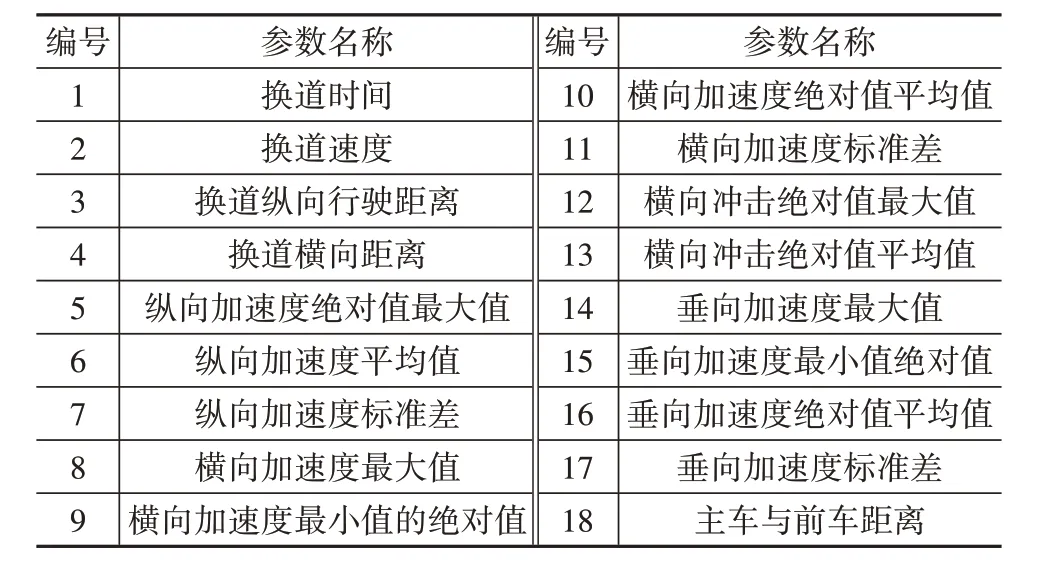
表3 换道过程参数

3 乘员舒适性综合评价方法

3.1 舒适性参数特征提取

根据行驶参数相关性，提取换道过程参数特征。设有p个原始变量xi（i=1，2，…，p）相关或者独立，将xi标准化得到zi为

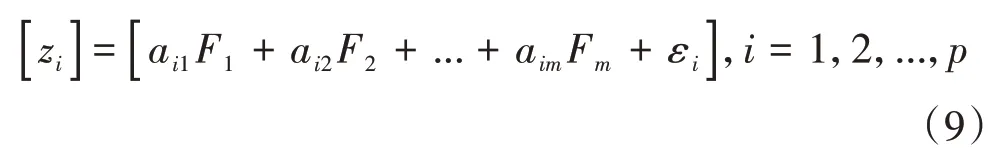
式中：Fj（j=1，2，…，m）为公因子；εi为特殊因子；系数aij为因子载荷。

归一化原始行驶参数并求得各个参数之间的相关系数：

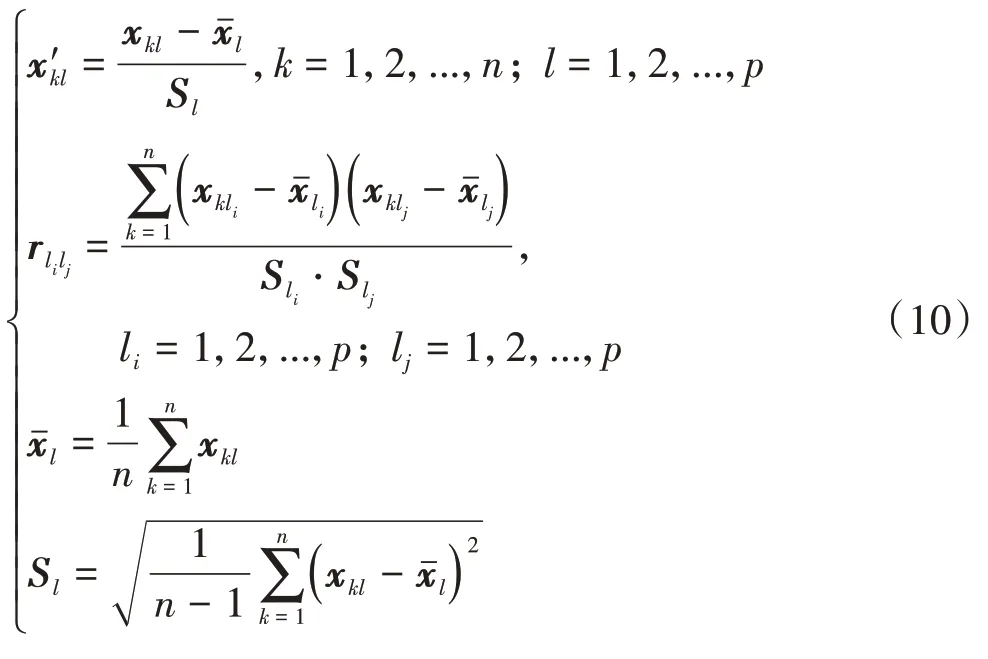
式中：n为样本总数；xkl、x′kl为原始行车数据和标准化数据；rlilj为相关系数。

对车辆行驶参数KMO进行检验，结果见表4，其中，KMO值为0.756 1，接近1；Bartlett检验的卡方统计值较大，相伴概率为0.00，小于0.005，适合因子分析。

表4 KMO和巴特利特检验

在原始特征参数相关系数矩阵rlilj的基础上，利用标准特征方程|λI-R|=0，得到相关系数矩阵的特征根λ（定义λ1≥λ2≥···≥λ18>0）和特征向量eig，且得载荷矩阵A：

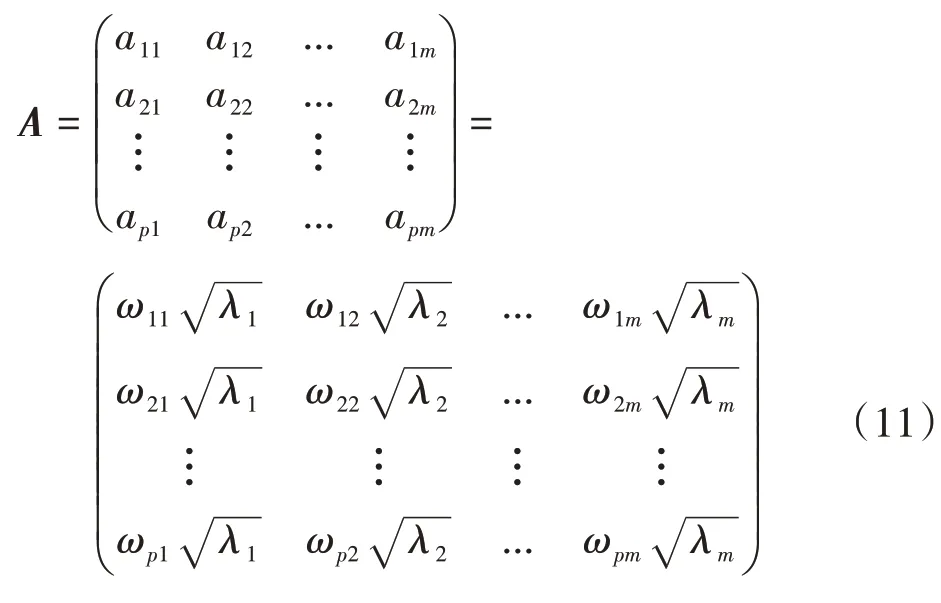
式中ω为标准化特征向量。

利用特征根占比得到公共因子的方差贡献率（vari）和累积方差贡献率（VARi），见表5，前5个特征根大于1的公因子方差累积贡献达80.6%，包含原始特征参数的大部分信息。

因子载荷矩阵各因子载荷系数差异较小，无法对因子命名，借助最大方差法旋转因子载荷矩阵得到因子载荷旋转矩阵RA，见表6，参数8-13为公因子1，主要为横向加速度的过程特征参数，故称为横向冲击因子；参数14-17为公因子2，主要为行驶过程垂向振动过程参数，称为垂向振动因子；参数5-7为公因子3，主要为纵向运动的过程参数，称为纵向加速因子；参数2、3和18为公因子4，主要和行驶过程的安全有关，称为风险因子；参数1、4为公因子5，主要影响换道行驶效率，称为效率因子。

公因子确定后，计算因子得分，忽略特殊因子ε，则因子得分系数和得分为

式中：SCi为公因子得分系数；Scorei为公因子得分。

3.2 舒适性客观参数与行驶参数辨识

3.2.1 因子加权和非线性加权模型辨识

对影响舒适性的5个公因子得分进行加权，并旋转因子贡献率，换道得分与舒适性加权方均根的关系见表7。

表7 贡献率和加权系数

从表7加权系数可得，行驶参数中，横向、纵向、垂向因子对乘员舒适性影响大于行驶风险和效率因子，将因子得分加权排序后与对应舒适性加权均方根均值得分见图9，对因子分析得分Tscore和加权均方根aw的相关性进行分析得rTa=0.73，因子贡献率加权相关性达73%，但不满足建立车辆行驶参数与舒适性客观指标的要求。

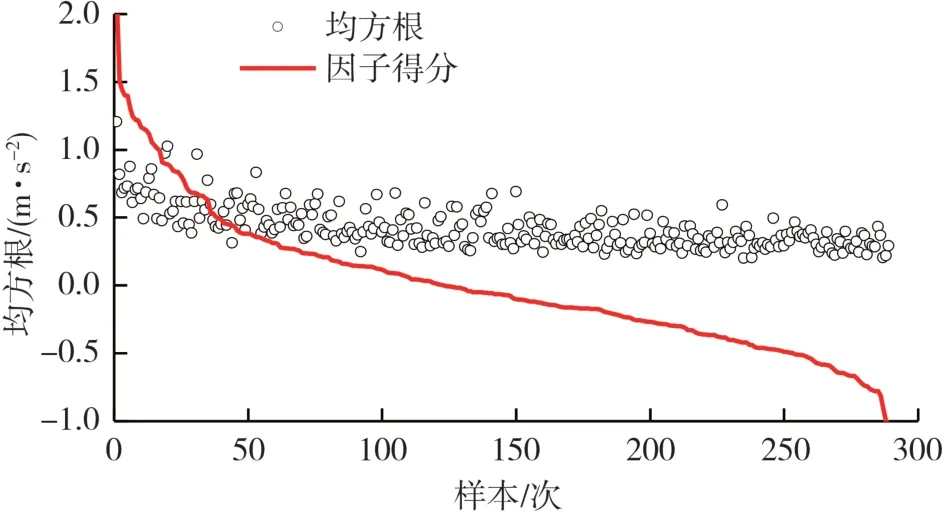
图9 Tscore和aw得分

为了辨识车辆行驶参数与乘员舒适性客观参数（舒适性加权均方根）的关系，基于因子贡献加权的思想，对因子得分进行非线性拟合：

式中k为多元非线性拟合加权数，得到的回归系数估计值和Scorei加权比例见表8。

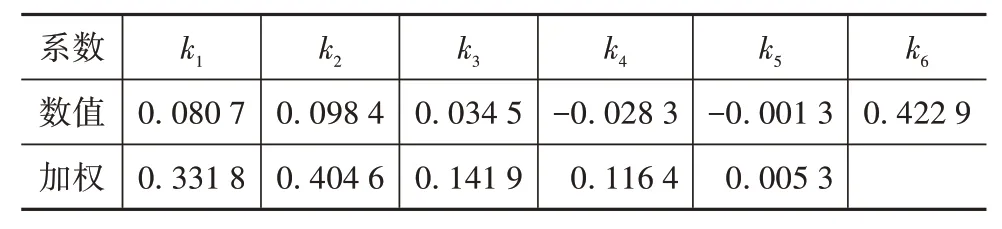
表8 非线性拟合回归系数估计值

多元非线性加权ap和aw的相关性rpw=0.871（见图10），拟合误差均值为0.057，大于0.05，且存在误差较大的点，无法辨识乘员舒适性。

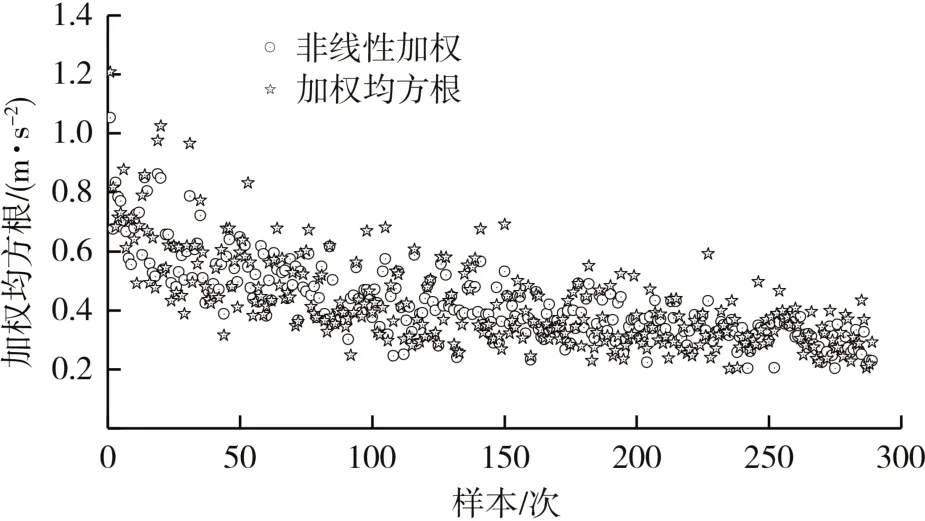
图10 多元非线性加权ap和aw

3.2.2 BP神经网络加权模型辨识

利用神经网络分布式并行信息处理，调整内部相互连接的关系，最大程度还原参数基本特征。

选取最速下降L⁃M算法为训练函数，设置两个隐含层。第1层激活函数选用双极S形函数、隐含层第2层和输出层为线性函数、训练误差为10-7、学习率为0.01、训练迭代次数为500次。为使训练函数快速收敛和选取最优化训练参数，结合最优粒子群算法原理，以隐含层节点数为自变量，输出anet和aw相关性为目标，寻求最优参数。最终确定隐含层第1层为5个节点，第2层为6个节点。

神经网络输出anet和aw相关性为0.939（见图11），误差均值为0.003。非线性加权误差与神经网络加权误差对比见图12，神经网络加权误差远小于非线性加权误差，既神经网络加权的准确率高，且样本可以随时扩充，鲁棒性强。

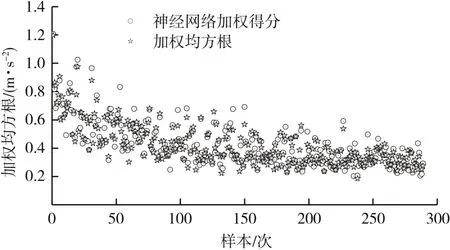
图11 神经网络输出anet和aw

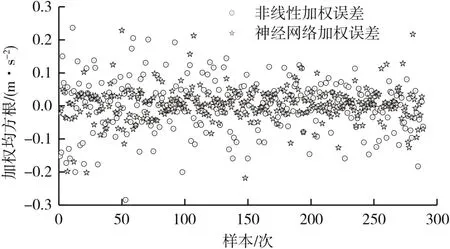
图12 多元非线性加权与神经网络加权误差

3.3 基于乘员闭环的个性化舒适性评价

传统乘员舒适性评价方法通过加速度均方根的阈值范围来评价，不能够定量定性对不同乘员的个性化舒适性进行评价。为了定量定性地研究乘员个性化乘坐舒适性，基于辨识模型估计乘员乘坐个性化舒适性，对92组乘员主观舒适度参数（换道整体舒适度分数、换道过程舒适度分数均值、换道过程最不舒适最大值）进行分析，见图13。其中，换道得分as1在2-8（分数越高舒适性越好）分之间，对分数进行等比例缩放得到as1=-as+0.95（分数越高舒适性越差），对as1和aw的相关性进行分析得rsw=0.858，主观舒适度和客观舒适度的相关性很高，能够辨识主客观舒适度关系。

图13 换道得分as1和aw

为了匹配不同乘员的个性化需求，降低主观统计的主观因素和噪声，基于卡尔曼滤波对不同乘员舒适性和个性化乘坐体验进行辨识，寻求不同乘员不同乘坐体验下舒适性加权参数阈值，基于系统的过程模型，对上一状态预测有

乘员舒适性和乘坐体验需求分为保守、平稳、激进风格，不同风格对于不同乘坐体验的舒适性约束阈值不同，基于卡尔曼滤波对某乘员平稳乘坐需求进行分析。其中输入参数为乘员体验主观平稳舒适评分所对应的舒适性加权均值，故卡尔曼滤波参数为：测量值Z（k）（舒适度加权均值）；Q为0；R为0.1（加权函数误差）；初始状态协方差P（1）为0.1；X（1）为乘员体验平稳舒适的多次客观舒适性加权均值。

从某乘员舒适性体验中评价为舒适且平稳的30组数据中，客观舒适性加权均值X（1）为0.313 3；随机抽取15组进行运算，15次运算后结果为0.312 2（见图14），误差小于0.001。

图14 卡尔曼滤波乘员舒适性识别

因此神经网络模型能够准确辨识行驶参数和乘员客观舒适性的关系，利用卡尔曼滤波能够快速对乘员的个性化需求进行识别。区别传统舒适性方法，对不同乘员乘坐舒适性需求进行了定量定性的研究，能够为考虑乘员舒适性的个性化轨迹规划和个性化驾驶风格进行定制。

4 结论

（1）为了满足自动驾驶系统对乘员乘坐个性化舒适性的需求，基于传统乘员乘坐舒适性理论，对舒适性影响参数和轨迹规划参数的关系进行分析，搭建了乘员闭环的个性化舒适性辨识理论体系。

（2）分析乘员乘坐舒适性理论，搭建自动驾驶系统数据和乘员舒适性采集平台，采集得到18个车辆行驶特征参数和量化乘员主客观舒适性参数。对行驶特征参数进行降维分析，得到横向冲击、纵向加速、垂向振动、行驶风险和行驶效率5个舒适性影响因子，利用因子加权、非线性加权和神经网络加权算法和卡尔曼滤波对行驶参数和主客观舒适性参数进行辨识，得到规划行驶参数对乘员舒适性的辨识模型。

（3）辨识模型的乘员主客观舒适度相关性高达85.8%；行驶参数中，横向、纵向、垂向因子对乘员舒适性影响大于行驶风险和效率因子，且个性化乘员舒适性辨识率高达93.9%；可为搭建考虑乘员舒适性的个性化轨迹规划控制算法提供理论依据。