测量学中关于坐标正算与反算问题的几点思考
2021-08-30蒋德兴
蒋德兴

摘要:大专院校和中职学校的土木水利类专业都开设有测量学课程,测量学课程的学习包括测量理论知识的学习和测量操作环节的实训,测量理论知识又分为测量基本概念和测量基本计算两个部分,基本计算包括高差高程的基本计算、角度的基本计算、坐标的正算与反算、坡度的基本计算等等。本文就测量学中坐标正算与反算的有关问题进行了思考。
关键词:测量;坐标正算;坐标反算;计算精度
中图分类号:TU198 文献标识码:A文章编号:1003-2177(2021)10-0072-03
0 引言
测量学中的所有计算既要保证公式的正确、正负符号的正确和计算单位的正确,同时又要保证计算精度达到要求,计算精度指的是计算量的准确程度以及计算量的有效位数。如果计算量不正确就谈不上准确程度,如果计算量正确但有效位数不够同样也谈不上准确程度。本文就测量学中坐标正算与反算的准确程度以及有效位数的取位问题进行了探讨。
1坐标正算
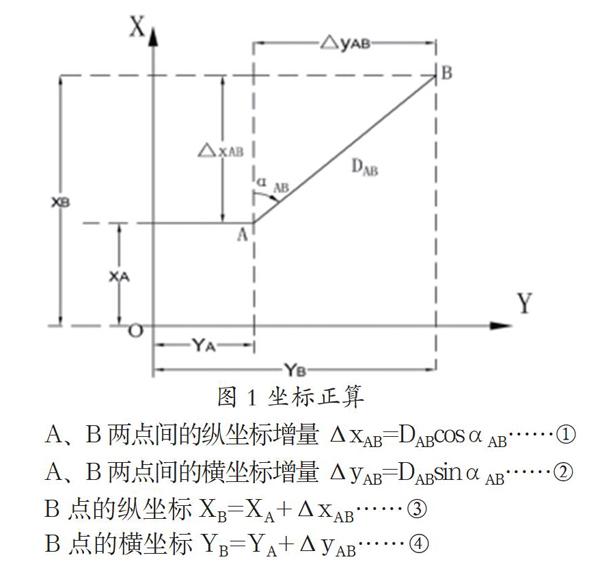
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标。如下图1所示,设直线AB的边长为DAB,坐标方位角为αAB,已知点A(起点) 的坐标为(XA、YA),则直线未知点 B(终点)的坐标计算如下[1]:
图1 坐标正算
A、B两点间的纵坐标增量ΔxAB=DABcosαAB……①
A、B两点间的横坐标增量ΔyAB=DABsinαAB……②
B点的纵坐标XB=XA+ΔxAB……③
B点的横坐标YB=YA+ΔyAB……④
由公式①、②计算A、B两点间的纵、横坐标增量ΔxAB、ΔyAB时,αAB一定要是已知点A到未知点B的坐标方位角,如果是未知点B到已知点A的坐标方位角αBA,那么一定要加或減180°变成已知点A到未知点B的坐标方位角αAB。由于边长DAB在工程上一般取三位,即精确到mm位,所以坐标增量ΔxAB、ΔyAB也精确到mm位,位数取多了意义不大,位数取少了精度不够。坐标增量的正负取决于三角函数值的正负,而三角函数值的正负又取决于坐标方位角所在的象限。当坐标增量为正时,其正号一般要求写上而不要省略[2]。
由公式③、④计算B点的纵、横坐标XB、YB时,就不存在收舍了,已知点坐标和坐标增量是几位,未知点纵、横坐标就是几位。
2坐标反算
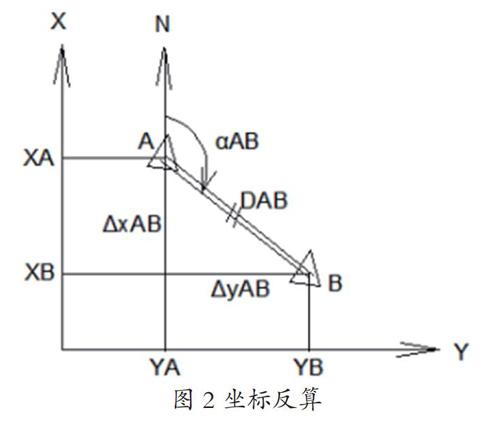
坐标反算,就是根据直线两个端点的已知坐标,计算直线的边长和坐标方位角。如下图2所示,若 A、B为两已知点,其坐标分别为(XA,YA)和(XB,YB),那么根据三角函数,可以得出直线边长和坐标方位角的计算公式为[1]:
图2 坐标反算
ΔxAB=XB-XA……⑤
ΔyAB=YB-YA……⑥
DAB=√[(xB-xA)2+(yB-yA)2]=√(ΔxAB2+ ΔyAB2)……⑦
tanαAB=(yB-yA)/(xB-xA)=ΔyAB/ΔxAB=K……⑧
αAB=arctan(K)+常数…… ⑨
常数与AB方向所在的象限有关,即与纵、横坐标增量的正负号有关,下表1列出了各个象限的常数值:
由公式⑤、⑥计算A、B两点间的纵、横坐标增量时,一定要用终点坐标减去起点坐标。对于水平距离而言,无所谓起点与终点,但对于方位角而言,必须分清楚起点与终点,如果计算的是AB方向的坐标方位角,那么A为起点,B为终点。如果坐标增量的大小没有错,而算错了正负号,后面对距离的计算没有影响,但对方位角的计算就有影响了,影响了方位角所在的象限。公式⑤、⑥在计算时无收舍,原本是几位有效位数,其结果也取几位有效位数。
由公式⑦计算边长时,一定要注意根号下需要一对中括号,否则就没有根号到第二项的值。计算结果一定有个取位问题,按照前面的叙述,已知坐标是几位,边长就取几位有效数字。
由公式⑧计算方位角的正切函数值K时,那么是否K也取与已知坐标相同的位数呢?答案是否定的!我们在工程上通常说坐标、边长以及坐标增量取三位有效数字就能保证精度了,但方位角的计算我们通常要求精度达到1″,在这里的正切函数值该取多少位呢?下面用数学中的微分方程来探讨这个问题:
将公式⑧两边取微分得到:sec2αAB·dαAB/ρ″=dK
dαAB=(dK/sec2αAB)·ρ″=(cos2αAB)dK·ρ″,式中ρ″=206265″。
为了讨论K的误差对αAB的最大误差影响,不妨取cos2αAB=1,下面列出表2。
从表2可以看出,当K取到小数点后面五位时,K的最大误差(dK)为0.000005,而αAB的最大误差(dαAB)为1.0″。在工程上,方位角的计算我们通常要求精度达到1″,所以我们得出重要结论:为了使方位角反算的精度达到1″,正切函数值K必须取到小数点后第五位。我们再来回答开始提出的问题:显然,如果函数值K也跟着坐标取三位的话,方位角的计算误差就有可能达到上百秒,这显然不能满足工程上方位角反算的精度达到1″的要求[2]。
文章的最后我要再次探讨方位角的反算公式:公式⑨是利用反正切函数求方位角,事实上当边长已经计算出来后我们还可以反正弦或者反余弦来求方位角,其公式如下:
由公式①可得到cosαAB=ΔxAB/DAB,αAB=arccos (ΔxAB/DAB)+常数……⑩
由公式②可得到sinαAB=ΔyAB/DAB,αAB=arcsin (ΔyAB/DAB)+常数……
我们在实际工作中,通常利用反正切函数来求方位角,而不用反正弦函数或反余弦函数来求方位角,其理由如下:(1)反正弦函数或反余弦函数求方位角时,要利用边长,而边长是计算值,有收舍误差。反正切函数求方位角时,不需要边长,这样就少了一次计算过程中的收舍误差。(2)反正切函数求方位角时,对于任何方向的方位角计算,其计算过程中的收舍误差都不会带来较大的方位角误差,而反正弦函数时,对于接近坐标南北方向的方位角的计算,由于ΔyAB的值很小,正弦函数值(ΔyAB/DAB)不会因为分母的计算误差而带来较大的误差,这种情况下反正弦函数计算方位角会比较准确,这时的ΔxAB非常大,非常接近于分母的值(边长),恰恰此时反余弦函数计算方位角的误差会比较大;对于接近坐标东西方向的方位角的计算,由于ΔxAB的值很小,余弦函数值(ΔxAB/DAB)不会因为分母的计算误差而带来较大的误差,这种情况下反余弦函数计算方位角会比较准确,这时的ΔyAB非常大,非常接近于分母的值(边长),恰恰此时反正弦函数计算方位角的误差会比较大。以下表3的数据为例我们进行验证。
从上表3可以看出:对于任意的方向,反正弦、反余弦、反正切所得的方位角基本一致;对于接近南北的方向,反正弦与反正切所得的方位角一致,而反余弦所得的方位角就与之相差较大;对于接近东西的方向,反余弦与反正切所得的方位角基本一致,而反正弦所得的方位角就与之相差较大。
3 结语
本文着重探讨了坐标反算中的取位和计算精确度的问题,并对方位角反算的三个公式作了对比,指出了其优缺点。
参考文献
[1]李仕东.工程测量[M].北京:人民交通出版社,2009.
[2]国家测绘局.工程测量规范(GB50026-2007)[S].
(责编:杨梅)
