时间受限下无人机无线携能传输效用最大化研究*
2021-08-30孙启明
孙启明,宋 绯
(陆军工程大学,江苏 南京 210001)
0 引言
随着万物互联的需求日益增长,物联网得到了广泛应用[1]。然而,物联网设备(Internet of Things Devices,IoTDs)由电池供电,在某些场景下充电不便,严重影响了整个网络的存续时间。无线携能传输技术(Simultaneous Wireless Information and Power Transfer,SWIPT)既能够传输数据,又能够从射频中获取能量[2],因此可以利用该技术延长物联网系统的工作时间。无人机作为机动灵活的空中平台,利用机载无线发射器,可以实现与地面设备的视距通信。
相关文献中已有对于该问题的研究。例如:文献[3]研究了无人机中继网络中无线携能传输吞吐量最大化问题;文献[4]研究了物联网节点接收能量最小者最大化问题;为了评估通信网络优化效果,文献[5]将节点通信速率总和作为效用函数;文献[6]将节点收集的能量总和与消耗能量之比作为充电效用。
本文研究无人机携能传输中效用最大化问题,设计了新的效用函数来评估系统性能。为了解决发射功率分配问题和优化飞行轨迹,提出一个无人机发射功率和飞行轨迹联合优化方案。采用文献[7-8]中的凸近似方法求解非凸问题,最大化携能传输的效用值。
1 系统模型与问题建模
1.1 模型建立
考虑一种场景,即在一定范围的区域内,多个IoTDs 随机分布,任务无人机从基地出发,对这些设备节点进行携能传输后返回基地,基地坐标为(0,0,0),如图1 所示。
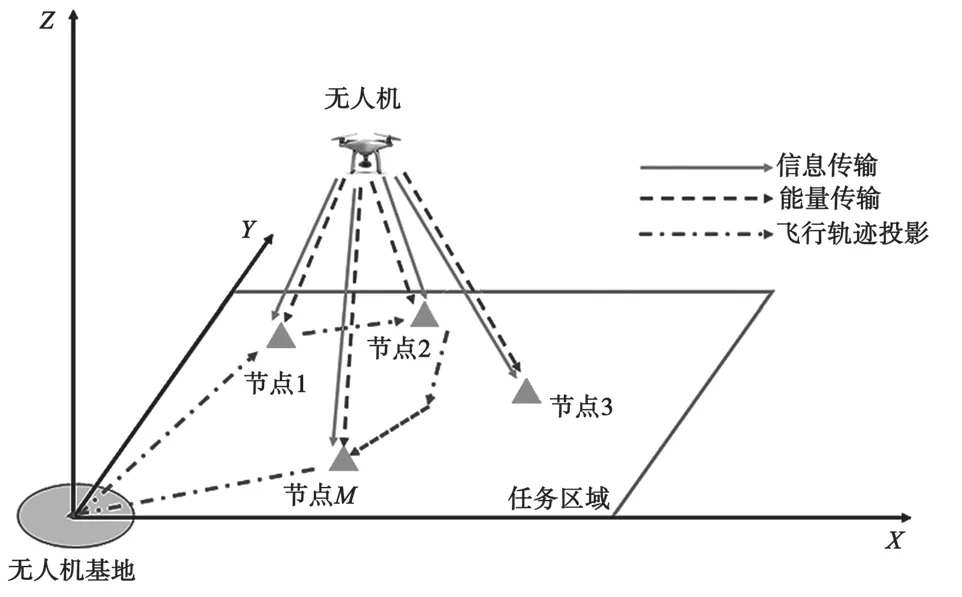
图1 无人机无线携能传输系统模型
假设地面节点的集合为M={1,2,…,m,…,M},每个节点坐标为(Xm,Ym,0),在水平面的投影为Wm(Xm,Ym),位置固定不变。无人机在有限时间T内执行任务,时间T被分为N个均匀时隙,时隙长度为δ,得到δ=T/N。一般时隙长度取足够小,这样使得无人机在某个时隙里的位置近似不变。设定无人机高度固定,其高度为h,在时隙n的位置坐标为(x[n],y[n],h),则无人机在水平面的投影为(x[n],y[n],0)。由于无人机硬件限制,最大飞行速度为Vmax,而且无人机执行完任务后要返回基地,无人机飞行轨迹在水平面的投影为L[n](x[n],y[n])。L[n]会有如下限制:
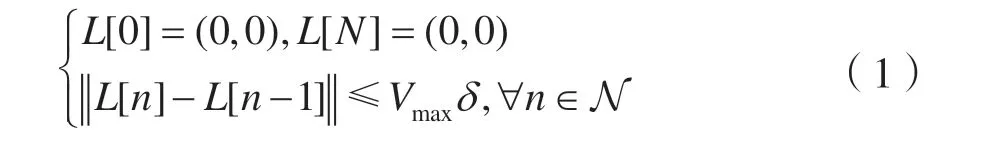
接下来考虑信道模型。在室外空旷地区,无人机与地面节点之间无遮挡,故可采用直射视距链路模型,如:
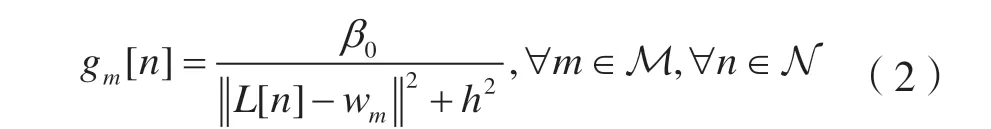
式中:β0为单位距离上的无人机与节点的信道增益。
视距链路模型中,信道增益随着无人机与节点之间的距离增加而单调减小,因此在保证飞行安全的情况下,无人机尽可能以最低高度飞行,避免频繁升高或者降低,取h为一个固定值。无人机同时与多个地面节点进行通信,通过划分不同频率的信道,将能量分配给各个节点。如图2 所示。
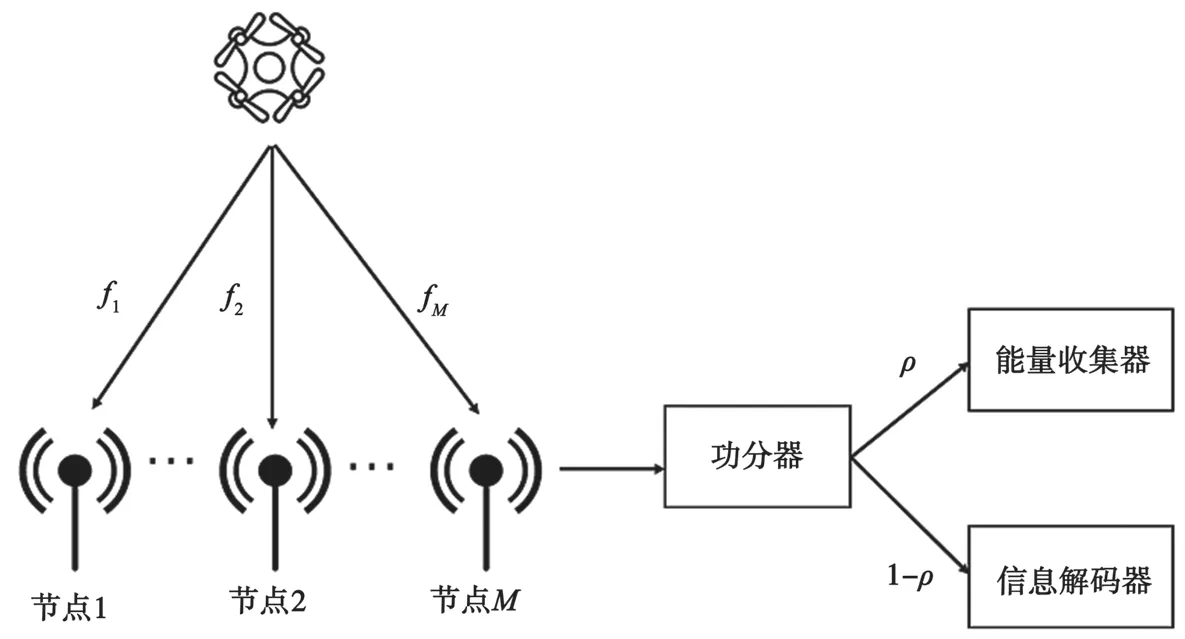
图2 功率分割法携能传输模型
在功率分割模型中,每个节点配备功分器,将采集到的能量按照比率ρ用于能量收集,1-ρ用于数据传输。
某一时刻无人机分配给所有节点的功率之和是有上限的,因此得到如下限制:

式中:PT为无人机的总发射功率;pm[n]为第n个时隙无人机分配给节点m的传输功率。根据上述功分模型,推导出在第n个时隙内,节点m从无人机射频中获取的瞬时能量为:

式中:η为节点设备进行能量采集的效率。
任务时间T内,第m个节点获取的总能量为:
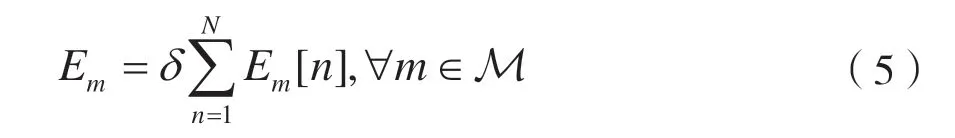
又根据香农公式,推导得出时隙n节点m的信息速率为:
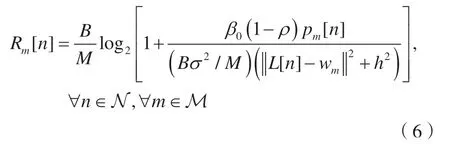
式中:B为系统总带宽;σ2为噪声功率谱密度。根据式(5)得到,在任务时间内,节点m从无人机射频中获取的数据量为:
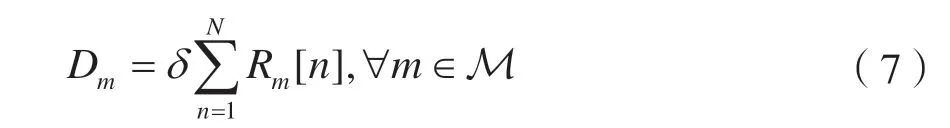
1.2 问题构建
在一些实际任务中,例如节点电池剩余能量严重不足的情况或者一些军事行动中,无人机的任务时间往往是受限的。因此需要在最小时间内获取最大的收益,收益包括获取的能量和数据量。为了综合评价无人机无线携能传输的性能指标,引入了效用函数的概念。效用函数既考虑系统获得的收益,又考虑了系统付出的代价。针对时间受限条件下的无人机无线携能传输,设计了一个全新的效用函数:

式中:ω1、ω2为加权系数。
为了保证系统能长时间稳定工作,需尽量避免饿死节点的出现,于是给每个节点设置一个最低能量需求。
本文研究的效用最大化问题建模如下:
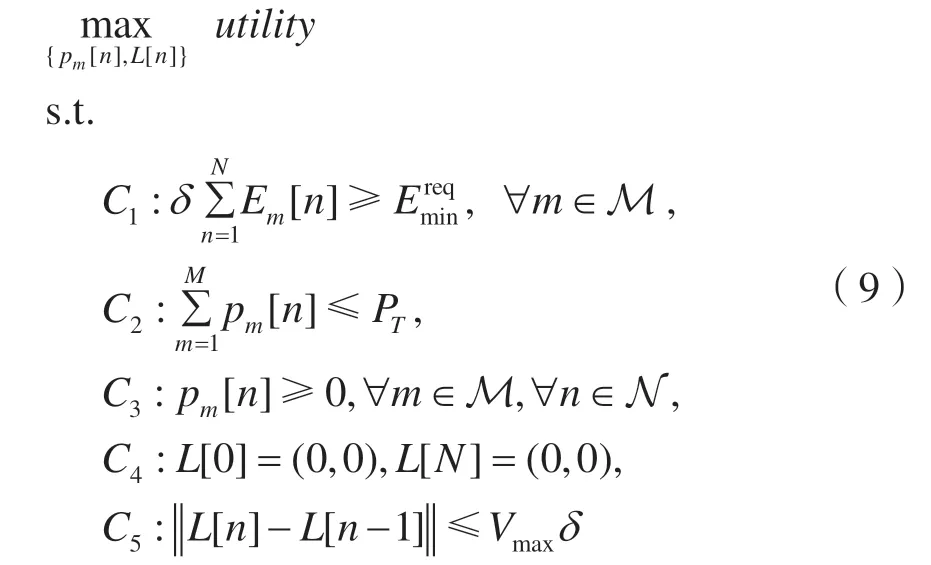
从目标函数和约束函数的表达式,可以看出这是一个非凸问题。为解决这个非凸问题,本文采用连续凸近似的方法,并提出一个无人机发射功率和飞行轨迹联合优化方案。
2 无人机发射功率与飞行轨迹联合优化算法
为了便于处理目标函数和约束函数中的表达式非凸表达式,引入变量u,则原优化问题改写成如下形式:

发射功率和飞行轨迹联合优化流程如图3所示。
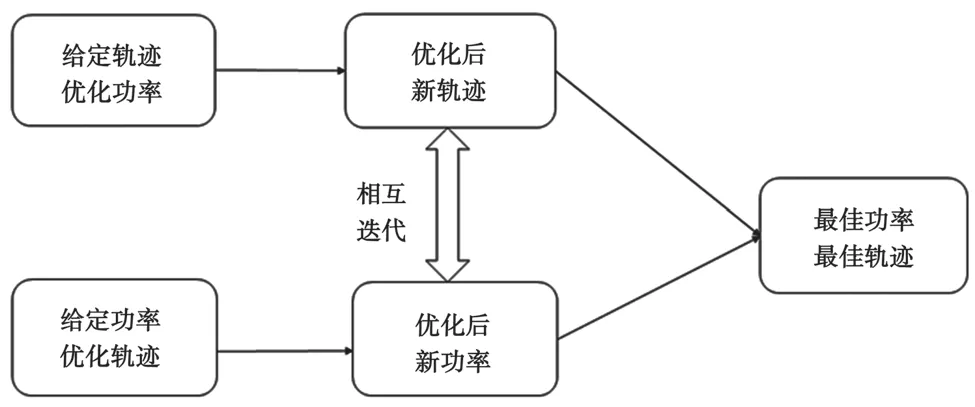
图3 联合优化流程
2.1 功率优化
在某些任务场景中,无人机需要按顺序依次访问各个物联网节点,并使得总飞行时间最短,飞行距离最小,以达到最优续航的目的。根据以上描述,这是一个典型的旅行商问题(Traveling Salesman Problem,TSP)问题。求解TSP 问题有很多成熟的算法,如遗传算法、蚁群算法等[9-10],但求解TSP问题不是本文的重点,故采用已有的遗传算法得到初始轨迹。无人机沿着固定的初始轨迹飞行,在飞行过程中进行功率优化。优化问题变成如下形式:

Em、Dm都是关于Pm[n]的凸函数,目标函数为两个凸函数的非负加权求和。因此,上述优化问题是一个典型的凸优化问题,可以用现有的凸优化方法解决。
2.2 轨迹优化
在一些场景中,无人机的发射功率是固定的,需要优化无人机的飞行轨迹。无人机的轨迹优化是无人机无线通信中一个非常关键的问题,因为无人机是运动的,可以通过不断改变位置获得最佳信道条件。轨迹优化问题表述如下:


根据以上推导,轨迹优化问题转化成如下问题:
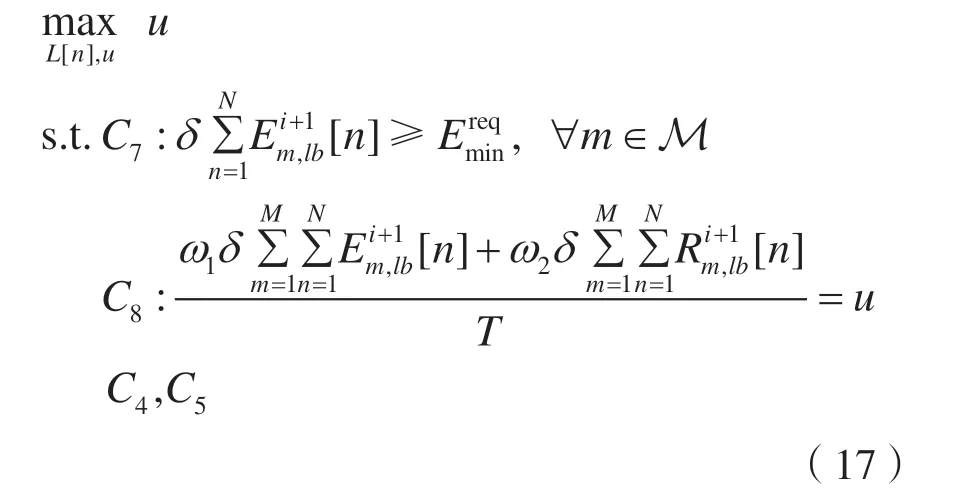
2.3 发射功率和飞行轨迹联合优化
发射功率和飞行轨迹联合优化问题是一个非凸问题,难以求出最优解。综合考虑计算复杂度和精度要求,将发射功率和飞行轨迹进行相互迭代,来得到次优解。
发射功率与飞行轨迹联合优化算法如下:
(1)设置无人机对各个节点的初始发射功率pm[n]和无人机初始飞行轨迹L[n],设置最大迭代次数和误差精度ε,迭代次数i=0;
(2)循环;
(3)输入无人机第i次迭代的飞行轨迹Li[n],求出第i+1 次迭代的最优发射功率,更新;
(4)循环;
(7)输出最终的效用值u,发射功率pm[n]、飞行轨迹L[n]。
3 仿真结果与分析
为了验证无人机发射功率和飞行轨迹联合优化算法的有效性,在MATLAB 平台上进行了多次的仿真。
3.1 参数设置
仿真参数如表1 所示。

表1 实验仿真参数
3.2 性能分析与对比
先根据仿真得出有最小能量约束条件时,不同任务时间无人机进行携能传输的效用值。无人机最大飞行速度为20 m/s。
不同任务时间的效用值如图4 所示。当能量约束较小时,效用值较大,这是因为无人机在满足了节点的最低能量需求后,就可进一步优化发射功率和飞行轨迹,使得最终的效用值更高。这反映了约束条件对目标函数的约束作用。时,T=35 s,效用值取得最大值。时,T=35 s,效用值取得最大值。时,T=30 s,效用值取得最大值。可以看出,效用值并不是随着任务时间单调递增或者单调递减。分析原因是由于在某些场景下,随着任务时间的增加,节点可以从无人机获取更多的能量和信息量。但随着任务时间继续增加,获取的能量和信息量增加并不明显,就导致效用值反而减少。综合以上分析,效用值的变化是切合实际的。
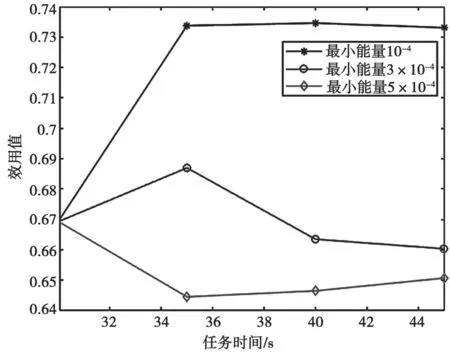
图4 不同任务时间的效用值
选取任务时间T=35 s,飞行速度V=20 m/s,研究无人机不同能量约束下的飞行轨迹如图5 所示。从图5 中可以看出,当能量约束较小时,无人机离独立节点较远,且在节点密集的区域停留较长时间,这样可以获得较大效用值。当能量约束增大时,无人机会抵进各个节点,才能满足各个节点的能量需求。
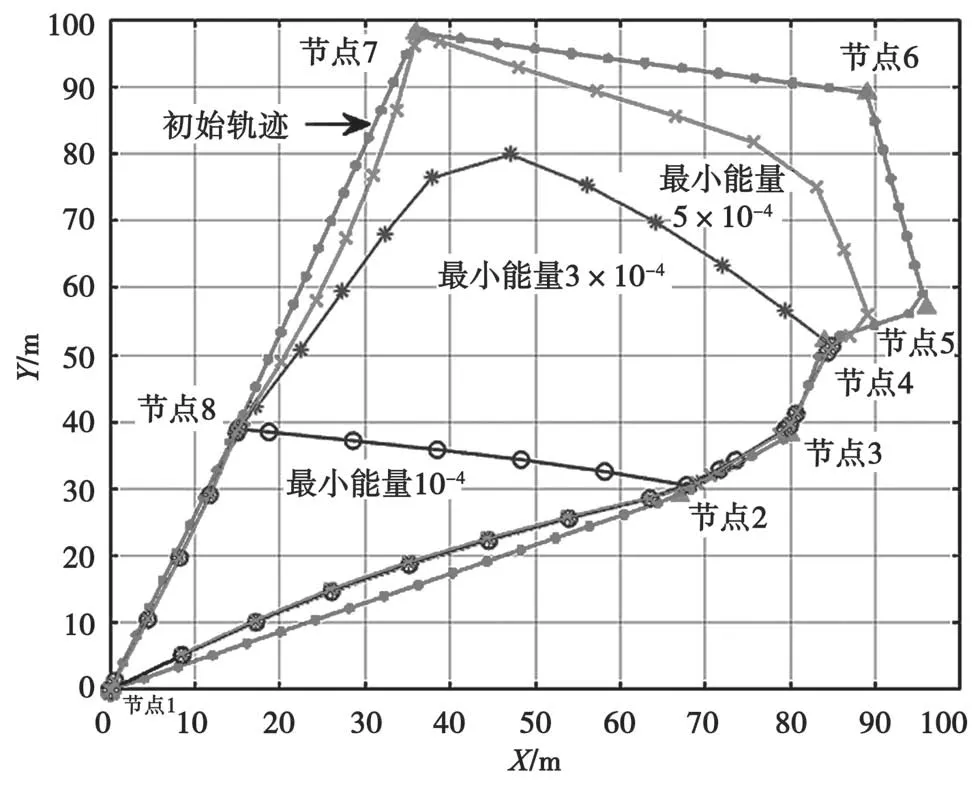
图5 不同能量约束下无人机飞行轨迹
结合无人机轨迹图、发射功率图(见图6)、飞行速度图(见图7),不难发现,无人机会在一些信道条件较好的位置盘旋,因为速度为0 m/s。信道条件不理想时,无人机会以最大速度飞往信道好的位置。同时也可以观察到,无人机越接近节点,分配给该节点的功率就越大。
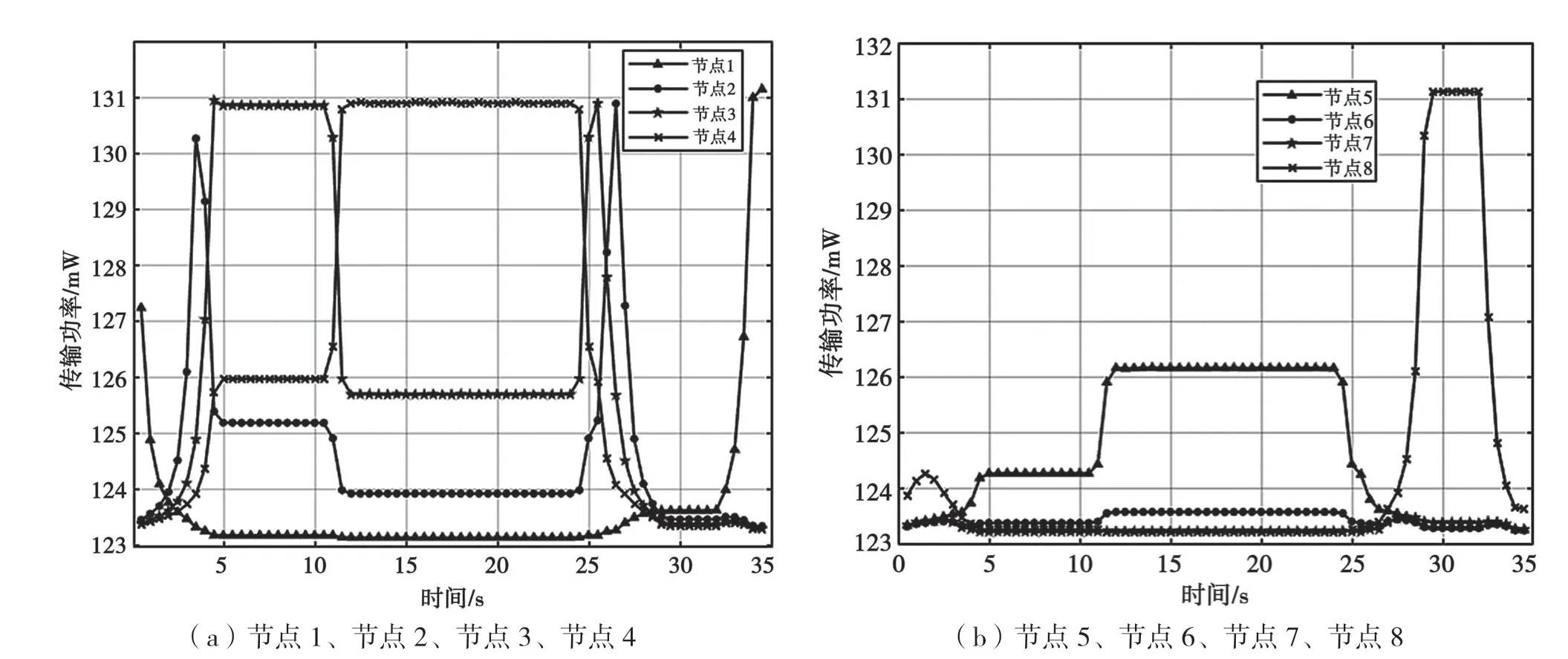
图6 无人机发射功率

图7 无人机飞行速度
为了评估联合优化算法的优越性,对比4 种场景下,功率优化、轨迹优化、联合优化3 种方法的效用值(见图8)。

图8 不同场景下3 种方法效用值对比
场景1:任务时间T=30 s,无人机最大飞行速度V=20 m/s,能量约束E=3×10-4mJ。
场景2:任务时间T=30 s,无人机最大飞行速度V=25 m/s,能量约束E=3×10-4mJ。
场景3:任务时间T=40 s,无人机最大飞行速度V=20 m/s,能量约束E=3×10-4mJ。
场景4:任务时间T=40 s,无人机最大飞行速度V=25 m/s,能量约束E=3×10-4mJ。
从图8 中可以看出,本文所提联合优化方法仿真得到的效用值均优于其他两种算法,原因是同时优化了功率和轨迹,使得无人机能够在更好的信道条件下,采取最优发射功率。
4 结语
本文研究了物联网系统中时间受限条件下无人机SWIPT 效用最大化问题。通过无人机发射功率和飞行轨迹联合优化,使得效用值达到最大,即在有限的时间内获得最大的收益。仿真结果验证了本文所提联合优化算法的优越性。
