分压器电路中多种方法研究总电阻的变化规律*
2021-08-30李国良
李国良
(兴义民族师范学院 物理与工程技术学院,贵州 兴义562400)
在电学恒定电流的学习中,电阻串并联电路[1-3]一直是研究的热点。在电阻串并联电路中,当分压器电路中滑动变阻器的触头滑动而使滑动变阻器并联部分阻值增大时,则串联部分阻值变小,即并联部分阻值和串联部分阻值变化相反,因而不能直接判断总电阻的变化规律。为了获得分压器电路中总电阻的变化规律,以前以滑动变阻器串联部分阻值为研究变量,并分别用构造函数法、求导法以及单调函数法进行了研究,并对这三种方法进行了比较[4]。在构造函数法中,构造可以直接判断分压器电路总电阻变化规律的特殊函数非常困难,求导法需要熟练掌握求导公式,而单调函数法的研究方法和推导过程都很简单。
下面以滑动变阻器并联部分阻值为研究变量,并分别使用构造函数法、求导法以及单调函数法对分压器电路总电阻的变化规律进行进一步研究。通过分别以滑动变阻器串联部分阻值和并联部分阻值为研究变量用这三种方法进行研究,并比较两个研究变量之间的差异,不仅可以使学生选择更合适的研究变量和研究方法,而且可以培养学生的思维能力,增强学生对学习物理的兴趣。
1 分压器电路总电阻的表达式
分压器电路是由滑动变阻器R1和固定电阻R2组成,如图1 所示。如果滑动变阻器R1的串联部分阻值设为x,并联部分阻值设为y,则总电阻可以表示为:

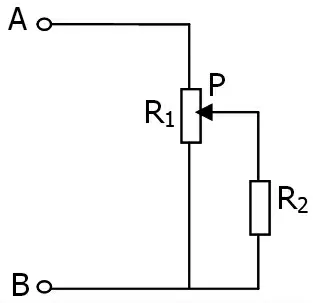
图1 分压器电路的电路图
当滑动变阻器的触头滑动时,由于并联部分阻值和串联部分阻值的大小变化相反,所以不能直接判断分压器电路总电阻的变化规律。为了判断总电阻的变化规律,并与以前以滑动变阻器串联部分阻值x 为研究变量进行比较,现在以滑动变阻器并联部分阻值y 为变量进行进一步研究,由公式(1)可以将总电阻表示为滑动变阻器并联部分阻值y 的函数,

总电阻的变化规律[5]:由滑动变阻器R1和固定电阻R2组成的分压器电路中,当R1的并联部分阻值y 增大时,总电阻R(y)减小。为了更加容易地判断分压器电路总电阻的变化规律,以滑动变阻器并联部分阻值y 为变量,用构造函数法、求导法以及单调函数法分别对总电阻的变化规律进行进一步研究,并与以前以滑动变阻器串联部分阻值x 为变量的研究结果进行比较,从而为选择更合适的研究变量和研究方法提供依据。
2 构造函数法
为了能够直接判断分压器电路总电阻R(y)的变化规律,可以将总电阻R(y)构造为这样一个特殊函数,即当滑动变阻器并联部分阻值y 发生变化时,总电阻R(y)中所有的y 引起总电阻的变化趋势一致,这就是构造函数法。由公式(2)可以看出,不好直接判断总电阻R(y)的变化规律,因此可以先将总电阻R(y)表示为:

当0 当0 以前以滑动变阻器串联部分阻值x 为研究变量,构造可以直接判断分压器电路总电阻变化规律的特殊函数时,构造过程非常困难。现在以滑动变阻器并联部分阻值y 为研究变量,构造可以直接判断分压器电路总电阻变化规律的特殊函数时,构造过程大大简化。因此,在构造函数法中,如果有多个研究变量,可以通过改变研究变量的方法来分别构造特殊函数,从而选择最佳的研究变量来简化构造特殊函数的过程。 首先将分压器电路总电阻R(y)对y 求导,即求出R′(y),然后将R′(y)进一步化为各个整式乘积的形式,最后由各个整式的正负来判断R′(y)的正负,从而判断出R(y)的单调性,这就是求导法。当0≤y≤R1时,如果R′(y)>0,则R(y)为增函数;如果R′(y)=0,则R(y)为减函数;如果R′(y)=0,则R(y)在y 值时恰好取极值,这时y 值两边单调性相反。 由公式(2),首先将R(y)对y 求导,可以得到R′(y)的关系式: 为了更容易地判断R′(y)的正负,可以将R′(y)进一步化为各个整式乘积的形式,由上式可以将R′(y)化为: 当0 可见,不论以前以滑动变阻器串联部分阻值x 为变量研究总电阻R(x)的变化规律,还是现在以滑动变阻器并联部分阻值y 为变量研究总电阻R(y)的变化规律,均需要熟练掌握求导公式,并化为各个整式乘积的形式,才能判断总电阻的单调性。当然,如果有多个研究变量,可以通过改变研究变量的方法来分别利用求导法,从而选择最佳的研究变量来简化研究过程。同时,有些函数的求导过程较难,对求导公式的熟练掌握要求较高。由于求导法不仅能够判断函数的单调性,而且可以在某点取函数极值,故在科研中常常用到求导法,如在长方体型消色差延迟器的设计过程中[6-7],就是利用取极值的方法对延迟器件进行设计。 设任意的变量y1、y2∈[0,R1]且y1 设任意的变量y1、y2∈[0,R1]且y1 由公式(7)可以看出,不好直接判断R(y1)-R(y2)的正负。为了更加容易地判断R(y1)-R(y2)的正负,可以将R(y1)-R(y2)进一步化为各个整式乘积的形式,则R(y1)-R(y2)可以化为: 由于0≤y1 可见,不论以前以滑动变阻器串联部分阻值x 为变量研究总电阻R(x)的变化规律,还是现在以滑动变阻器并联部分阻值y 为变量研究总电阻R(y)的变化规律,单调函数法不仅研究方法都很容易掌握,而且推导过程都很简单。只要掌握单调函数法的方法,并化为各个整式乘积的形式,均可以利用单调函数法较快地判断总电阻的单调性。因此,单调函数法是一个非常好用的研究方法。当然,如果有多个研究变量,可以通过改变研究变量的方法来分别利用单调函数法,从而选择最佳的研究变量来简化研究过程。 由于单调函数法在判断函数单调性的过程中,研究方法简单容易掌握,故在科研中作为一个较为常用地数学工具,如在AD-2 型消色差延迟器件的设计过程中,为了判断函数f1(θ)和g1(θ)的单调性,就是通过单调函数法进行判断[8]。可见,单调函数法在科学研究中有着非常重要的应用。 当然,在利用构造函数法、求导法以及单调函数法研究分压器电路总电阻变化规律的过程中,不管是以滑动变阻器串联部分阻值x 还是以滑动变阻器并联部分阻值y 为研究变量,在变量研究的区域上均为增函数或减函数这种较为简单的情况。如果在研究的区域上既有单调增加又有单调减小这种较为复杂的情况,则一般先用求导法求出极值点,然后选择合适地研究变量和研究方法在多个单调区域上分别判断单调性。 在研究分压器电路总电阻R(y)变化规律的过程中,以滑动变阻器并联部分阻值y 为研究变量,分别用构造函数法、求导法以及单调函数法对分压器电路总电阻R(y)的变化规律进行进一步研究,得到了分压器电路总电阻的变化规律。与以前以滑动变阻器串联部分阻值x 为研究变量相比,构造函数法在构造特殊函数的过程中大大简化;求导法和单调函数法的难度基本不变,另外求导法需要熟练掌握求导公式,单调函数法的研究方法和推导过程都很简单。 因此,研究分压器电路总电阻变化规律过程时,与以滑动变阻器串联部分阻值x 为研究变量利用单调函数法求解较为简单相比,以滑动变阻器并联部分阻值y 为研究变量,利用构造函数法和单调函数法求解都较为简单。 当然,以上主要分析在变量研究的区域上为增函数或减函数这种较为简单的情况。如果在研究的区域上既有单调增加又有单调减小这种较为复杂的情况,则一般先用求导法求出极值点,然后选择合适的研究变量和研究方法在多个单调区域上分别判断单调性。
3 求导法
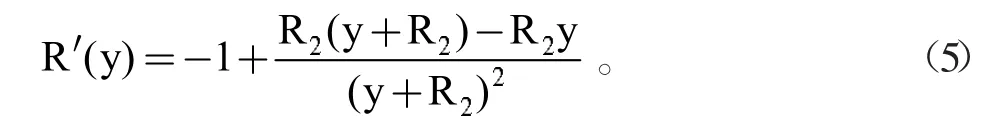

4 单调函数法


5 结束语
