基于推理表现水平进阶的猜想、说理与例证——《比的基本性质》同课异构教学解析与思考

文|宋煜阳（特级教师）

推理能力作为小学生必备的数学核心素养之一，是学生数学学科能力中的一项核心能力，是提升学生学科核心素养的关键。培养和发展学生的推理能力，是数学教学的重要目标。

推理能力是否得到发展，本质上是学生推理表现水平进阶的反映。而刻画学生推理表现水平，既需要选取典型的课例作为学习载体，又需要整个推理活动过程加以贯穿。猜想、说理和例证是推理能力表现水平的重要元素，同时又是推理学习过程的核心活动，为此，围绕推理表现水平进阶，对《比的基本性质》教学中的猜想、说理与例证等活动的讨论，具有重要的意义。

一、表现水平的进阶：理解与刻画教学目标的重要基点

《比的基本性质》一课，作为六年级上册的推理内容学习，它究竟承载着怎样的教学目标？我们有必要回到《数学课程标准（2011年版）》相关目标要求来思考。如第二学段课程内容目标指出，“在观察、实验、猜想、验证等活动中，发展合情推理能力，能进行有条理的思考，能比较清楚地表达自己的思考过程与结果”；又如在实施建议中提出要处理好“合情推理与演绎推理的关系”，要“通过实例使学生逐步意识到，结论的正确性需要演绎推理的确认，可以根据学生的年龄特征提出不同程度的要求”等。

问题在于，对于六年级学生来说，怎样才算是能比较清楚地表达自己的思考过程？演绎推理怎样的程度要求才算是适切的？特别是，我们该如何为即将升入第三学段的学习对象作出必要的衔接？这一系列问题，都需要借助推理能力表现水平指标将相关课程目标具体化。

参照徐斌艳教授“数学学科核心能力框架模型”研究成果，推理能力表现水平可划分为记忆与再现、联系与变式、反思与拓展三个层次。各水平层次的表现指标和本课例表现行为作如下描述。

水平一：记忆与再现。

主要表现指标：能够形成一些合理的猜测；能够有条理地表达获得猜想的推理过程；能够在简单情境下解释命题的正确性。

课例表现行为：能对“比的基本性质”作出猜想，但表述不完整；能通过举例子、计算比值进行不完全归纳说明，但缺少大量例证和反例意识；验证意识、论证过程的完整性都需要引导。

水平二：联系与变式。

主要表现指标：能在较复杂的问题情境下提出认知水平层次较高的猜想；能清晰地表述思考过程；能够联系他人的推理与已有经验进行解释。

课例表现行为：能对“比的基本性质”作出猜想，会用语言完整表述；能采用不完全归纳推理的方法来进行说理，知道例证的基本要求；能读懂他人利用“除法与比的关系”“商不变性质”演绎推理得出“比的基本性质”的过程与方法，初步学会利用“分数与比的关系”仿照进行演绎推理，但不能独立完成整个演绎推理过程。

水平三：反思与拓展。

主要表现指标：能够获得更多猜想，对结论进行反思和检验；有理有据地表达，说理充分；能通过枚举归纳和演绎推理两种思路进行解释说明。

课例表现行为：能对“比的基本性质”作出猜想，会用语言完整表述，并能对后续“比例”的性质以规律形式进行猜想；在不完全归纳推理的基础上，能利用“除法与比的关系”“分数与比的关系”“商不变性质”“分数的基本性质”等数学事实进行演绎推理，独立完成整个过程，能说出每步推理的依据。

作为推理活动的核心元素，猜想、说理和例证成为推理表现水平进阶的关键。为此，两个课例在猜想、验证（推理）过程上给出了充足的活动时空，同时在活动要求上也给出了较高的要求。就推理能力表现水平进阶而言，两节课例的学习活动目标定位都是合理的，也是必要的。

二、知识经验的联结：推进猜想与说理活动的重要抓手

在“比的基本性质”之前的学习中，学生经历了多次规律和性质的探究归纳、举例说理活动，积累了一定的“猜想”“验证”等推理活动经验。因此，如何有效激活知识经验之间的内部联结、实现学习者的自主迁移，成为本课推进猜想与说理活动的重要抓手。

就猜想与说理活动板块来说，本课主要有两个地方的知识经验内部联结。

联结一，关于分数、除法和比之间的知识内联，包括三者各部分名称和三条性质之间的等价联结。此处的联结目标主要指向两个：一个是帮助学生激活经验，开展合情推理活动，根据商不变性质、分数的基本性质内容，对新的“比的基本性质”进行类比猜想；另一个是利用三者等价关系的转化进行说理，开展各类推理活动，这是推理表现水平进阶的节点，也是本课的学习难点与关键。课例教学中，两位教师都非常重视这个知识内联的激活与延展。鲍老师是借助“关于比，你有哪些了解”“‘基本性质’不是第一次见了，你还记得哪些‘基本性质’？”“猜想一下，比的基本性质会是怎样的？”等问题，展开复习回忆并完成“比的基本性质”类比猜想。王老师则借助具体学习任务巧妙展开，先给出等值的一组数与算式（，组织学生观察讨论它们的相同之处和不同之处，激活三者之间的关系；紧接着通过“0.3÷0.5”的快速求值，激活商不变性质，进而类比猜想“比的基本性质”。尽管知识联结的手法略有不同，但都有效激活了分数、除法和比之间的知识内联，既快捷达成了类比猜想的联结目标，又为后续利用三者关系说理奠定了扎实的基础。

联结二，关于不完全归纳推理的经验内部联结，联结目标主要是调用学生举例验证、判断说理的已有经验方法，对新的“基本性质”进行论证。教学中，两位教师都围绕“从严格意义上讲，只能验证你们举的例子是成立的，这些例子能说明所有的比都成立吗？”“举例子是数学证明中常用的方法，只是这样的一、两个例子就能证明刚才的猜想成立吗？”等核心问题，展开正例数量与结论可靠性之间的思辨，既有利于学生推理表现水平从“记忆与再现”向“联系与变式”提升，又增进了学生的质疑意识。特别是鲍老师，在得出比的基本性质后还进行了方法回顾、梳理，有助于学生向“反思与拓展”这一推理表现水平进阶。

三、推理路径的丰富：体会例证数量与方式的重要支点

“基本性质”的推理路径学习经历了三个阶段，分别是：在“商不变性质”中学习归纳推理；在“分数的基本性质”中侧重学习归纳推理，补充了解演绎推理；在“比的基本性质”中将归纳推理、演绎推理整体推进学习。整个推理路径学习序列呈现从单一到丰富、从侧重合情推理到两类推理整体推进的特点，而这个特点既可以视为推理表现水平进阶，也是对课程标准实施建议“处理好合情推理与演绎推理的关系”“根据学生的年龄特征提出不同程度的要求”的具体理解。

从两节课例实际教学来看，“比的基本性质”推理路径主要有不完全归纳推理、科学归纳推理和演绎推理三类。两位教师都基于结论的正确性，围绕例证的数量与论证方式对推理路径加以丰富并穿插比较。

当学生呈现惯用的不完全归纳推理方法时，两位教师都对其特点与局限进行了及时点拨，如“这些例子能说明所有的比都成立吗？”“这样的一、两个例子就能证明刚才的猜想成立吗？”等问题，帮助学生明确不完全归纳推理的论证基本思路是“举例验证———不完全归纳确认结论”，体会它是需要大量例证支撑，结论确定性存在一定风险的特点。在此基础上，抛出“还有其他方法说明这个结论一定成立吗？”“他没有求比值，能说明它们相等吗？”等问题思考，进而呈现另外两类推理路径。其中，王老师充分结合图1 中材料展开推理依据的追问，并形成图2 的板书图，帮助学生借助个例中除法、比、商不变性质之间的因果关系，实现了科学归纳推理，了解了“举例——寻找因果关系——确认结论”。在鲍老师的课堂上，学生直接将除法和比联系在一起，通过“比的前项相当于被除数，比的后项相当于除数，比值就是商，因为除法中有商不变性质，所以比的前项和后项同时乘或除以一个不为0 的数，比值不变”，推导得出结论成立，呈现了较为完整、清晰的演绎推理路径。两位教师都非常重视说理依据的追问，强调“有理有据地表达”。如果两位教师能够对后两类推理路径的特点与步骤进行及时点拨，比如“这样的验证需要多少个例子？”“这样验证的基本步骤是什么？”将促使学生对推理路径多元化和优化有更深的体会，也将有助于“反思与拓展”表现水平的达成。

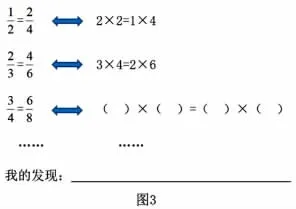
两节课例虽说同课异构，但都以推理表现水平进阶为目标，以猜想、说理和例证为抓手，以丰富推理路径为手段，呈现许多相似性。同时，后测研究表明两节课例的学习成效都达到了较高水平。其中，对后续“比的基本性质”教学中采用找规律（图3）、解释说理（图4）的方式进行了测查统计，近20%的学生解释说理时能够将比转换成分数形式，再利用图3 获得的规律作为前提进行演绎推理，表明学生已经达到了“反思与拓展”水平层次，实现了推理表现水平的进阶。