紧凑拉伸断裂韧性试样加载线位移推算方法的对比分析

2021-08-30佟振峰鱼滨涛张长义宁广胜钟巍华

理化检验(物理分册) 2021年8期

林虎,佟振峰,2,鱼滨涛,张长义,宁广胜,钟巍华,杨文

(1.中国原子能科学研究院,北京 102413;2.华北电力大学,北京 102206)

断裂韧性试验是核电厂反应堆压力容器(RPV)辐照脆化监督试验的重要组成部分。由于试样具有放射性，该试验的开展较常规断裂韧性试验更具有难度。因为试验操作难度大，会采用易于装卡操作的端面变形测量直通型C(T)紧凑拉伸断裂韧性试样。根据相关标准[1-4]，在试样端面测试得到变形数据后，还需要用特定方法推算出试样的加载线位移，因此加载线位移推算方法的准确性对于试验结果的准确性具有重要意义。目前并未形成统一的推算方法，不同的方法计算精度也不相同。

断裂力学是材料科学与力学的交叉学科，有关文献显示，在断裂韧性测试技术发展的过程中，计算技术非常重要，计算结果与试验方法有良好的一致性，使得结果的精度更高。近年来很多断裂韧性测试方法的研究工作都是通过有限元技术完成[5-9]。

美国ASTM E1921与我国NB/T 20292标准中采用的方法来自于LANDES[5]的研究成果；GB/T 21143-2014中提供的推算方法来自于西南交通大学蔡力勋团队的研究成果[6-7]；俄罗斯报告中并未给出推算方法的研究文献。

为了确定最合理有效的加载线位移推算方法，借助有限元技术开展了相应研究。该次试验采用Abaqus软件，模拟了RPV辐照脆化监督中最常用的0.5T-C(T)试样的变形过程。计算过程中材料本构参数参照RPV材料A508-3钢的拉伸试验结果[10]。

1 断裂韧性试验

1.1 标准C(T)试样

标准C(T)试样如图1所示[1-4]，试样销钉孔的连线上有用于装卡引伸计的台阶，引伸计可以装卡在此位置上用来直接测加载线位移。

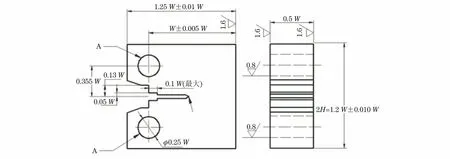
图1 标准C(T)试样示意图Fig.1 Schematic diagram of standard C(T)specimen

1.2 辐照脆化监督试验试样

由于辐照脆化监督试验的特殊性，试验中大多是采用图2所示的端面变形测量0.5T-C(T)试样，测量试样变形的引伸计装卡在试样的最外端，裂纹的两侧。通常这种断裂韧性试样被称为直通型C(T)试样[3]，主要用于线弹性条件下的脆性断裂试验，可以简便测定断裂韧性KIC[1-3,11-12]。

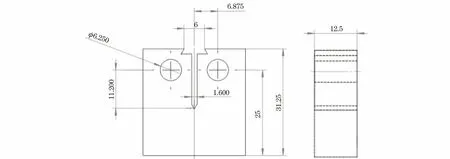
图2 端面变形测量的0.5 T-C(T)试样示意图Fig.2 Schematic diagram of front face deformation measurement of 0.5 T-C(T)specimen

RPV采用低合金铁素体钢制成，如A508-3钢，其具有较好的韧性[10]，即使是在材料的韧脆转变区进行断裂韧性试验依然不会发生完全的脆性断裂。在塑性变形能较大的情况下，必须获得试样的加载线位移，以便计算产生断裂能量中的塑性能分量[1-4,8-9]。

1.3 现有文献中的加载线位移推算方法

为了解决加载线位移推算的问题，部分断裂韧性试验标准会给出推算公式，包括美国ASTM E1921、俄罗斯РД ЭО 0350-02、我国的NB/T 20292、GB/T 21143-2014等标准。

NB/T 20292与ASTM E1921标准采用LANDES[5]的早期研究成果，认为端面位移v0与加载线位移vLL之间存在固定比值0.73，如下式所示：

vLL=0.73v0

(1)

俄罗斯方法则认为v0与vLL之间的比值为与裂纹长度有关的函数，如下式所示：

(2)

式中：W为图1所示裂纹宽度；a为裂纹长度，是两销钉孔中心之间的加载线到裂纹尖端的距离。

蔡力勋团队的相关研究指出可以采用等式(3)～(5)推算加载线位移[6-7]。目前此项研究成果已经写入GB/T 21143-2014中。

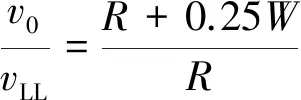
(3)

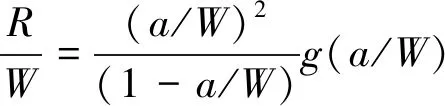
(4)

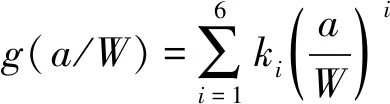
(5)

式中：R为试样转动半径；g(a/W)为无量纲的塑性转动因子；k0=150.155 4，k1=-1 427.620，k2=5 712.630，k3=-12 131.87，k4=14 357.50，k5=-8 967.939，k6=2 309.530。

GB/T 21143-2014中给出的转换方法是较为复杂的，主要是因为针对式(3)中的转动半径R参数给出了一种复杂的计算方法。一种通常的简单做法是采用较为简单的下式计算转动半径R：

R=(W+a)/2

(6)

将式(6)代入式(3)中即可简单得到转换比值，笔者称此方法为国标简化方法。虽然国内研究成果产生年代较晚，但是在研究过程中并未参考LANDES的研究成果。

2 加载线位移推算方法的验证

2.1 有限元方法

断裂力学的测试技术相关文献显示，断裂韧性的有限元计算结果与试验结果有良好的一致性，并且精度更高[13]。近年来很多断裂韧性测试方法的研究工作都是通过有限元技术完成的[8-9,13]。笔者也选用有限元方法来进行断裂韧性试样变形过程的模拟计算。

2.2 有限元模型

计算工作采用Abaqus软件进行，按照图1和图2建立平面应变模型,如图3所示，为了降低计算量，根据轴对称原则，模型只模拟了实际试样的一半。模型单元格尺寸为0.2 mm，采用八节点缩减积分平面应变单元，裂纹尖端将八节点四边形单元畸形化成三角形单元，并且将侧面单元向畸形顶端移动至0.25倍边长位置。求解计算方法为有限变形方法。图3显示的模型按照裂纹长度尺寸分为4组，对应裂纹a/W取值为0.5、0.55、0.6、0.652，另外每一组模型又对应3种材料本构。

图3 断裂韧性试样的有限元模型Fig.3 Finite element model of the fracture toughness specimen

2.3 材料本构

采用简单幂硬化材料作为材料本构[8]，对于单向拉伸，当拉应力达到σ0时，开始发生塑性变形。应力应变关系如式(7)～(9)所示：

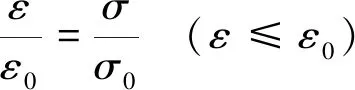
(7)

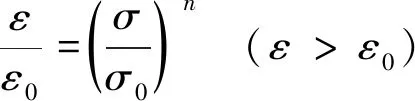
(8)

(9)

式中:ε为轴向拉应变；ε0为当轴向拉应力达到σ0时的轴向拉应变；σ为轴向拉应力；σ0为参考屈服应力；n为幂硬化指数；E为杨氏模量。

各个参数通过A508-3钢的拉伸试验结果确定[10]。为了表征A508-3钢在试验温度附近温度区域的应力应变关系，选用3组材料性能参数进行计算：

(1)E=209 GPa，σ0=480 MPa，n=5，泊松比ν=0.3；

(2)E=209 GPa，σ0=430 MPa，n=11，泊松比ν=0.3；

(3)E=209 GPa，σ0=530 MPa，n=12，泊松比ν=0.3。

2.4 计算结果

计算得到v0/vLL的比值如图4所示，有限元计算得到的数据呈现明显的规律性。在0.5～0.65的a/W区间内，GB/T 21143方法的曲线在有限元结果之间穿过；俄罗斯方法曲线高于有限元计算结果；国标简化方法曲线低于有限元计算结果；NB/T 20292方法与ASTM E1921方法曲线走向与有限元结果呈现交叉，从有限元计算结果之间穿过。在a/W等于0.75时，GB/T 21143方法曲线低于有限元计算结果，但是与其他曲线相比，其依然是与有限元结果最接近的。

图4 不同材料v0/vLL的有限元计算结果和不同推算方法计算结果Fig.4 The calculation results of finite element and different inferring methods of v0/vLL of different materials:a)the material 1;b)the material 2;c)the material 3

3 分析与讨论

GB/T 21143方法曲线与计算结果符合性最好，二者之间存在明显的相关性，较其他方法有较大优势，a/W在0.50～0.65区间内较为有效；俄罗斯方法和国标简化方法曲线与有限元结果走向是接近的，但是存在明显的偏差，需要进行修正；现行NB/T 20292方法与ASTM E1921方法曲线与有限元结果走向完全不一致，但是与其存在交叉点，a/W在0.55～0.57的小范围内计算结果较为准确。

式(1)是最简单的加载线位移推算方法，但是用其计算得到的vLL较有限元计算值明显不一致，特别是当a/W处于较大值时计算得到的加载线位移vLL较有限元计算值小很多。虽然在a/W等于0.55时与有限元计算得到的结果较为接近，但是在a/W等于0.65时计算得到的塑性能会低于实际值2%以上，在a/W等于0.5时计算得到的塑性能略微低于实际值，这不利于得到准确的KIC。

俄罗斯方法曲线明显高于有限元得到的数据点，计算得到的加载线位移vLL较有限元计算值更小，这会造成计算得到的塑性变形能偏小，测量得到的KIC也会偏小。在a/W等于0.55时计算得到的塑性能会低于实际值2%以上。

国标简化方法与俄罗斯方法正好相反，计算得到的加载线位移vLL较有限元计算值大，这会造成计算得到的塑性变形能偏大，测量得到的KIC也会偏大。在a/W等于0.55时计算得到的塑性能会高于实际值2%以上。