不同牵引总重下C80型货车车钩载荷谱演化分析

卓 卉，朱 涛，俞正宽，肖守讷

(1. 国家能源投资集团有限责任公司, 北京 100120；2.西南交通大学 牵引动力国家重点实验室, 四川 成都 610031)

随着重载铁路的不断发展，列车的编组数量、速度和牵引总重不断提高，连挂车辆之间的纵向载荷也随之增大，使车钩的受力条件更为恶劣，导致钩体和钩舌等车钩组成部件的裂纹故障率增加。研究车钩的裂纹萌生和扩展寿命，需根据实际情况制定的合理的车钩载荷谱对其进行疲劳台架试验和数值仿真。

20世纪80年代，美国采用线路实测的方法对多种不同货车进行了线路测试，得到货车车体以及关键零部件的载荷谱，归纳整理后编入AAR机务标准手册的《货车设计制造规范》中。此外，力拓矿业公司等也通过实际线路测试得到了重载货车的载荷谱，并对典型工况下的零部件疲劳可靠性进行了分析[1]。我国对铁路货车载荷谱的研究始于20世纪80年代，1988年，中国铁道科学研究院联合上海铁道学院等单位在上海—齐齐哈尔以及上海—深圳这2条线路上进行了车钩载荷谱测试，同时完成了13型车钩的载荷谱编制工作；2006—2016年，北京交通大学在我国大秦线、神朔线和朔黄线等主要的运煤线路上进行了一系列的车钩载荷谱研究测试，并依据实际测试车钩载荷谱对车钩的疲劳寿命进行了预测[2-3]。

本文主要针对神朔线和朔黄线这2条运煤线路，分别对1万t和2万t重载列车货车车钩力进行仿真分析，并与现有实测的1万t重载列车货车车钩载荷谱进行对比分析[4]，在此基础上通过对载荷进行相应的修正，得到更接近于实际的2万t重载列车货车车钩载荷谱，以用于车钩疲劳台架试验。

1 车钩力仿真

1.1 仿真线路条件

在神朔线和朔黄线上实际运行的货车，去程为重车，返程为空车。

1.1.1 神朔线

神朔铁路由大柳塔至朔州西，整个神朔段铁路的剖视图大致上呈现W形走势，最高海拔高度约为1 500 m，最低海拔高度约为833 m，最大的上下坡坡度均为12‰。图1为神朔线仿真分析中的海拔落差设置。

图1 神朔线仿真分析中的海拔落差设置

1.1.2 朔黄线

朔黄铁路西起神池南，与神朔铁路相连，东至黄骅港，全线总长581.2 km。线路以下坡为主，包含2段长大下坡道：神池南站至原平南站路段，最大坡度为-12‰，平均坡度为-9.1‰；南湾站至古月站路段，最大坡度为-12‰，平均坡度为-7.2‰。图2为朔黄线仿真分析中的海拔落差设置。

图2 朔黄线仿真分析中的海拔落差设置

1.2 列车编组

结合神华铁路货车运输有限责任公司(以下简称“神华货车公司”)现有的货车编组形式与实测线路数据进行对比，综合考虑分析后设置的相关仿真列车编组和牵引总重如表1所示。

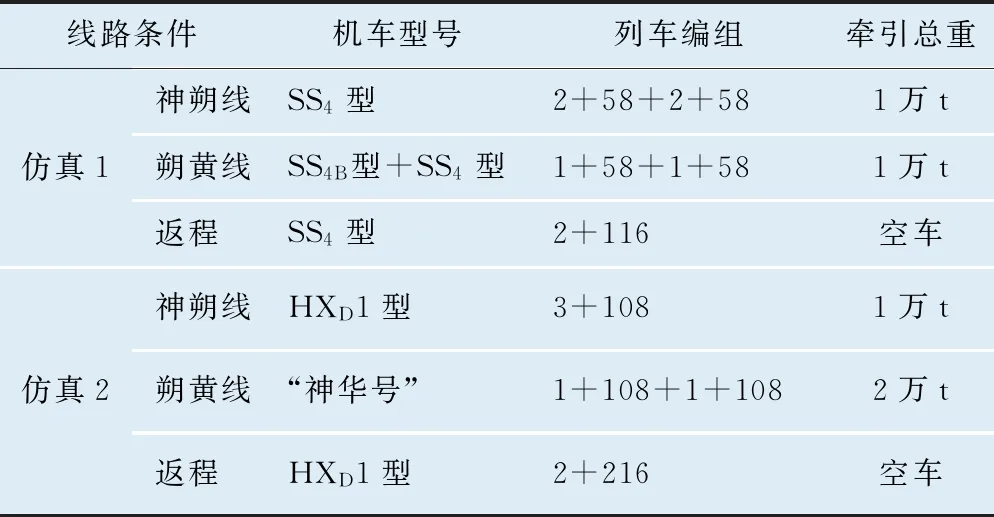
表1 仿真1和仿真2列车编组和牵引总重情况

1.3 车钩力-时间历程

仿真1和仿真2的最恶劣钩位车钩力-时间历程如图3和图4所示。

图3 仿真1最恶劣钩位车钩力-时间历程

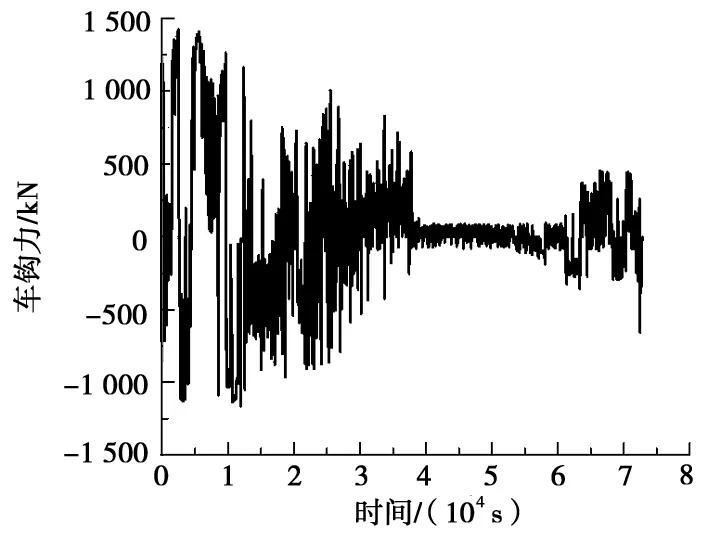
图4 仿真2最恶劣钩位车钩力-时间历程

仿真1的列车编组形式和实测1万t重载列车车钩载荷谱的列车编组形式相同，仿真的最大车钩拉力为1 059 kN；仿真2的列车编组形式与神朔线1万t和朔黄线现有的2万t重载列车编组形式相同，仿真的最大车钩拉力为1 421 kN。

2 载荷谱处理

将仿真得出的载荷谱和实测的载荷谱按照统一的方法进行处理，并对其频次和载荷幅值进行相应的统计。具体的处理流程如图5所示。

图5 载荷谱处理流程图

以下按照载荷谱处理流程对实测的1万t重载列车货车车钩载荷谱进行处理。

首先在车钩力-时间历程中将车钩压缩载荷去除，保留拉伸载荷。

通过雨流计数法得到的载荷具有不同的数值，需要对其进行转换，依据Goodman等寿命曲线将所有载荷转换成脉动循环载荷。试验中的最小载荷取值为50 kN，因此统一将各个循环载荷转换成最小值为50 kN的脉动循环载荷。

零部件受到的载荷小于疲劳极限时，应力强度因子小于门槛值，不产生损伤，对疲劳寿命不产生影响，因此去除该载荷以下的无损伤载荷。根据参考文献[5]，结合货车车钩实际运用情况和仿真分析结果，选取车钩钩舌下牵引台上长度为60 mm、深度为12 mm的裂纹，施加不同的载荷并计算其应力强度因子，和材料试验测试得出的门槛值(216.85 MPa·mm1/2)进行比较，得出一个下限载荷值。研究结果显示：对车钩施加80 kN的载荷时，其裂纹处的应力强度因子在门槛值以下，可认为80 kN以下的载荷对裂纹扩展几乎不会产生影响。因此在载荷谱处理时可以将小于80 kN的载荷去除。

以50 kN作为台架试验的最小起始加载载荷，并根据载荷的大小对载荷进行等间隔划分，以1 200 kN作为最大载荷、200 kN作为最小载荷，不同载荷级别间隔200 kN，所有真实载荷均按照分级的上限载荷进行处理，例如1 069 kN取值成1 200 kN；996 kN取值成1 000 kN，以此类推。根据以上准则对实测的1万t重载列车货车车钩载荷谱进行分级处理，共分成6级载荷谱，相应的统计频次如表2所示。

表2 实测1万t重载列车货车车钩载荷谱初步统计表

根据表2的统计结果可以看出，在列车的一个往返过程中，车钩受到的小载荷的循环次数占比较高，因此需要根据损伤当量折算，把相应的小载荷折算到大载荷上，以提高台架试验的效率。损伤当量折算公式为：

(1)

式中：neq——折算后的载荷频次；

Sai——折算前的载荷；

Seq——折算后的载荷；

ni——折算前的载荷频次；

m——材料参数，对于钢材而言，m=3[6]。

根据上述方法对仿真1和仿真2的载荷进行相应的处理，得到最终的载荷幅值和频次统计如表3所示。

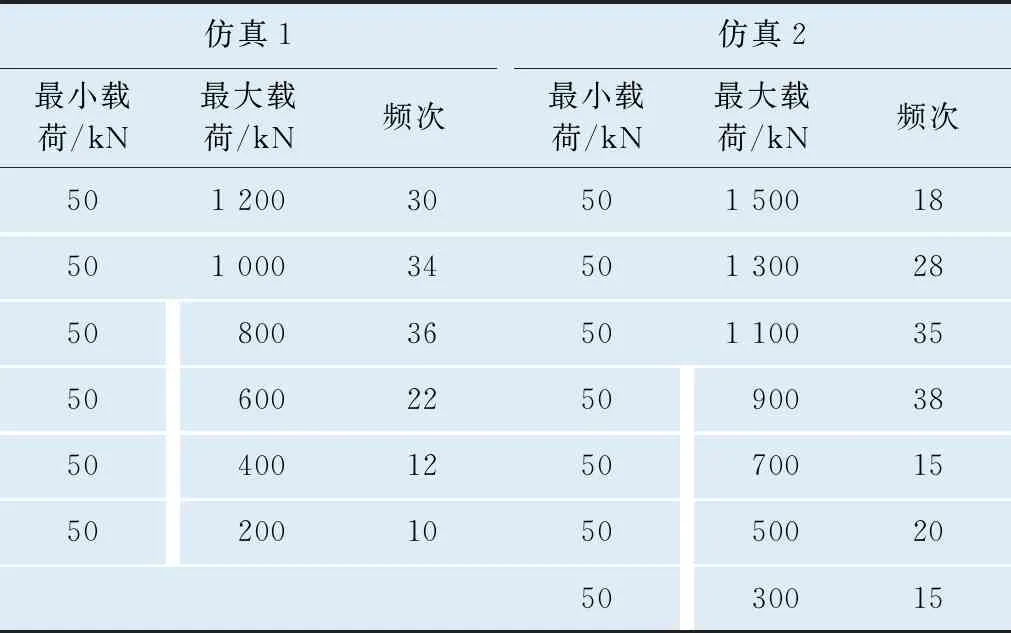
表3 仿真1和仿真2载荷谱最终统计

3 载荷谱对比修正

依据损伤当量折算方法可以将所有等级的载荷换算至同一等级，并且将不同工况下的载荷谱换算至同一频次下，这样能更直接地对载荷幅值进行比较。车钩载荷谱处理结果对比如表4所示。

表4 车钩载荷谱处理结果对比

综合以上的仿真分析结果，考虑到台架试验载荷的准确性以及与真实线路的匹配性，对实测车钩载荷谱进行适当放大以与目前线路的真实载荷进行相应的匹配。

仿真1的输入条件和实测车钩载荷谱一致，将所有载荷转换至同一频次下时，实测载荷谱的载荷放大系数为仿真的1.052倍，由式(1)可知，二者之间的损伤倍数为1.0523=1.16，即实测载荷谱的总损伤为仿真1总损伤的1.16倍，二者的误差较小，总体误差在20%以内，进一步验证了仿真1仿真结果的可靠性。

仿真2是依据目前神华货车公司现有2万t重载列车编组进行的仿真，将仿真2和仿真1的载荷进行对比，得出其载荷放大系数为仿真1的1.23倍，同理，得出仿真2的损伤为仿真1的1.233倍，即1.86倍，可见2万t牵引总重下载荷对车钩疲劳损伤影响更大，因此需要对实测1万t重载列车货车车钩载荷谱进行相应的修正，以得到近似于实际2万t重载列车货车车钩载荷谱。修正原则为：实际2万t重载列车货车车钩载荷谱=(仿真2载荷谱/仿真1载荷谱)×实测1万t重载列车货车车钩载荷谱。

由于仿真2的载荷放大系数为仿真1的1.23倍，出于安全考虑，取1.25作为载荷放大系数对各级载荷幅值进行相应放大，频次不变，得到的车钩载荷谱如表5所示。

表5 修正后的仿真2车钩载荷谱

疲劳试验载荷谱的加载类型主要有“低-高”“低-高-低”和“高-低”3种。不同的加载次序下对结构疲劳寿命的影响不同，根据参考文献[1]，采用“低-高-低”加载方式时的疲劳寿命与实际加载情况相近，为此车钩疲劳试验载荷谱选用短周期、且“低-高-低”的加载方式。

在实际的车钩疲劳台架试验中，将频次放大10倍作为一个循环，得到可用于车钩台架试验的最终载荷谱，如表6所示。

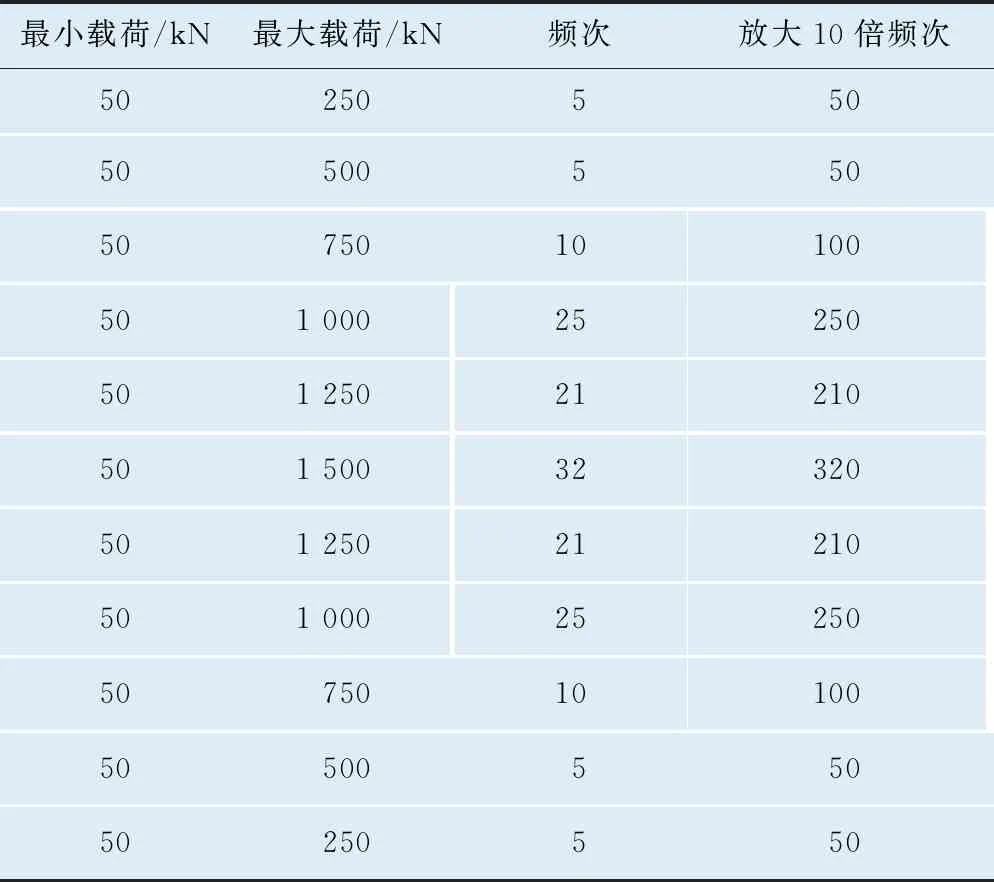
表6 车钩疲劳台架试验最终载荷谱

表6中，频次总计为164次，放大10倍后总计为1 640次。频次为164次的载荷谱对应朔黄线一个来回的里程为1 640 km；在台架试验过程中，将载荷谱频次放大10倍作为一个循环，此时一个循环下的频次为1 640次，对应里程为16 400 km。

4 总结

本文对神华货车公司1万t和2万t重载列车的货车车钩力进行了仿真分析，并以实测的1万t重载列车货车车钩载荷谱为基准，采用仿真对比分析的方法，得到了2万t重载列车货车车钩载荷谱。结论如下：

(1) 以神华货车公司实际线路条件和列车编组为输入对车钩纵向力进行仿真计算，将1万t重载列车货车车钩载荷谱的仿真结果和实测结果进行对比，验证了仿真模型的可靠性。

(2) 基于雨流计数和等损伤理论等方法，对仿真的1万t、2万t重载列车以及实测的1万t重载列车的货车车钩载荷谱进行处理分析，并进行相应的修正，由此得到了2万t重载列车的货车车钩纵向力载荷谱，研究成果对车钩疲劳寿命仿真和货车台架试验具有较高的工程运用价值。