基于运营数据的某型动车组转向架可靠性分析

刘 伟，张冬梅，高 磊

(中车青岛四方机车车辆股份有限公司 技术中心，山东 青岛 266111)

动车组转向架系统是动车组的走行装置，具有承载、牵引、减振、导向等重要功能，其系统可靠性直接影响动车组车辆的稳定性和安全性。在实际运营中转向架系统一旦发生严重故障，将导致列车晚点、线路瘫痪，甚至造成人员伤亡。因此，对转向架系统进行可靠性研究分析，对保证动车组运营安全、提高维修效益和避免不必要的经济损失及人员伤亡具有重要意义。

本文将以某型动车组转向架(运行3年)运行数据为基础，按一定原则进行数据筛选，对转向架各子系统运营过程中的故障数据进行分析，利用可靠性模型并结合统计学理论对转向架及各子系统的故障发生规律及可靠性进行统计分析，提出各系统可靠性评估指标，建立可靠性模型。并在可靠度允许的条件下，针对转向架现有的维修计划，对某些部件的维修周期进行优化，最终达到提高预防性维修的目的。

1 可靠性数据分析

故障分为非关联故障和关联故障[1]。在进行转向架系统可靠性分析时剔除非关联故障，用关联故障进行数据统计。非关联故障包括以下几个方面：

(1) 未按规定的条件使用引起的故障。包括损耗件在超过寿命期后使用所出现的故障；列车超载或超速状态下出现的故障；列车的使用环境条件超出了设计允许的范围；操作或维修人员的疏忽或不遵守操作规程导致的故障；操作和维修作业不按提供的操作和维修手册的要求进行；由于预防性维护工作失误导致的故障；因非转向架设备导致的故障。

(2) 某项不再采用的设计和工艺所引起的故障。包括：在可靠性指标测试期内出现的故障经采取设计或工艺改进措施后彻底排除、经证实不再发生者；嵌入式软件发生的故障经修改源程序并通过测试和实际使用证实不再发生者；原材料和元器件出现的故障，改用相同品种规格但质量更好的原材料和元器件后经证实不再发生者。

(3) 意外事件导致的故障。包括：非列车本身问题导致的碰撞、事故；故意破坏；自然灾害；由于公众(包括乘客)行为或疏漏导致的故障。

(4) 其他非关联故障。包括：经证实系机内测试(BIT)或车载诊断系统的错误而发生的虚警(实际未发生故障而发生的错误报警)，只计入虚警次数而不计为故障次数；连带故障(由前级故障导致的故障)等。

2 可靠性分析模型

常见的故障分布类型有指数分布、威布尔分布、正态分布等[2]。

2.1 指数分布

很多产品特别是电子元器件、无余度的复杂系统，在工作时间内可能由于 “偶然”的原因而发生故障，且在偶然故障期内故障率趋于某一稳定值。描述这种故障率为常数的分布函数是指数分布函数，即：

F(l)=1-e-λl

(1)

其故障间隔里程的概率密度函数为：

f(l)=λe-λl

(2)

可靠度函数为：

R(l)=e-λl

(3)

式中：λ——部件或系统故障率；

l——部件或系统故障间隔里程。

2.2 威布尔分布

威布尔分布一般适用于大型复杂系统的可靠性分布。产品从早期就可能发生故障，系统服从两参数的威布尔分布，假设形状参数为β，尺度参数为η，则威布尔分布函数满足：

(4)

其故障间隔里程的概率密度函数为：

(5)

可靠度函数为：

(6)

故障率函数为：

(7)

2.3 正态分布

故障服从正态分布，其故障间隔里程的概率密度函数为：

(8)

式中：μ——均值，表示系统或部件平均故障间隔里程；

σ——标准差，表示数据的离散程度。

3 转向架系统可靠性分析

3.1 转向架系统故障数据统计

转向架系统分为拖车转向架和动车转向架，拖车转向架包括构架组成、轮对轴箱组成、一系悬挂、二系悬挂、基础制动装置及附件装置等，动车转向架还包括齿轮箱驱动装置。

统计分析某型动车组(运营3年)的转向架系统运行数据，涉及转向架系统正线运行和库内维修的故障数据共1 586条。根据数据统计原则，剔除非关联故障835条，得到转向架系统关联故障751条，分析统计各子系统的故障数据如表1和图1所示。

表1 各子系统故障统计数据

图1 各子系统故障占比图

从上述统计结果可知，构架组成发生故障次数较少，附件装置发生故障的占比最大(主要是撒砂和排障装置)，其他各部件发生故障的占比相差不大。

3.2 转向架数据分析

为初步判断转向架系统故障的分布类型，通过直方图分析统计(组距为5×105km)，得到转向架及各子系统在不同运营里程内的故障数据统计结果，如表2所示。

由表2可绘出转向架系统故障频次直方图，如图2所示。转向架系统故障累计频次结果如图3所示。

表2 转向架及各子系统故障数据统计 次

由图2可知，随着运营里程的增加，转向架系统故障频次呈现先递增后减少的趋势，转向架系统的故障间隔里程呈威布尔分布。由图3可以看出，随着运营里程的增加，转向架系统故障累计频次增加，表明转向架故障属于耗损性故障。

图2 转向架系统故障频次直方图

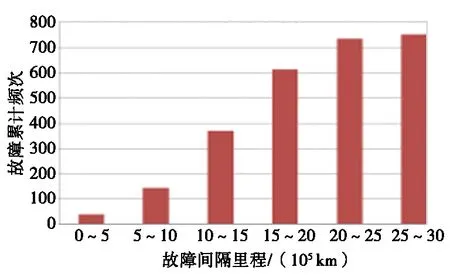
图3 转向架系统故障累计频次图

3.3 转向架各子系统可靠性模型分析

根据上述转向架系统故障数据处理结果，对转向架各子系统进行可靠性分析，得到各子系统可靠度曲线，为优化修程提供参考。因篇幅所限，本文以二系悬挂装置子系统为例进行可靠性模型分析。

本文利用中位秩和最小二乘法对η和β做参数估计。假设某部件的n个使用可靠性数据{li,i=1,2,...,n}，设F(li)为li时刻的中位秩，由统计学基本知识可知，中位秩近似公式为：

(9)

对式(4)进行变形，得：

(10)

两边取对数，得：

βlnl-βlnη=ln{-ln[1-F(l)]}

(11)

令

则有：

Y=AX+B

(12)

(13)

使用Excel自带的最小二乘法分析函数即可完成数据的拟合，并能完成置信度检验和线性相关程度检验。

经计算，二系悬挂装置子系统部分故障数据如表3所示。

表3 二系悬挂装置子系统部分故障数据

使用间隔计算模板，选择回归分析，设定置信度95%，对表3中自变量X与因变量Y进行回归分析，线性拟合结果如图4所示。

图4 线性拟合结果

由图4可得，线性拟合的斜率为2.677 8，截距为-38.537，将截距与斜率进行转换，可得威布尔分布形状参数β=2.677 8、尺度参数η=1 775 867，故威布尔分布函数为：

(14)

故障间隔里程的概率密度函数为：

(15)

可靠度函数为：

(16)

故障率函数为：

(17)

二系悬挂装置子系统可靠度曲线如图5所示。由图5可知，在可靠度为0.9时，运营里程为765 294 km。

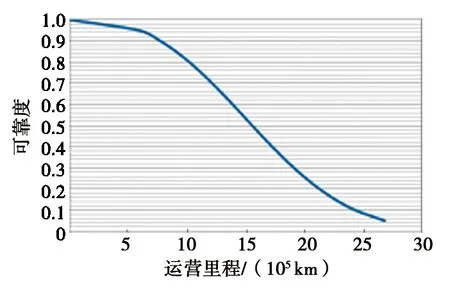
图5 二系悬挂装置子系统可靠度曲线

二系悬挂装置子系统故障概率曲线如图6所示。该故障概率曲线并不是典型的浴盆曲线，表示该子系统没有出现耗损期，但随着运营里程的不断增加，该子系统发生故障的概率在不断增加。

图6 二系悬挂装置子系统故障概率曲线

同样方法可得出其他子系统的威布尔分布。算出各子系统在可靠度为0.9(根据工程经验，用户可接受的可靠度不低于0.9)时的运营里程，如表4所示。

表4 各子系统可靠度为0.9时的运营里程 km

4 转向架维修计划分析

动车组转向架检修分为5个等级。一级和二级检修为运用检修，主要检查转向架状态；三级、四级和五级检修为高级检修。三级修是指新造、四级修或五级修后运行60万 km进行的修理；四级修是指新造或五级修后运行120万 km进行的修理；五级修是指新造或五级修后运行(480±12)万 km进行的修理。

以三级修为例，在子系统可靠度为0.9的情况下，根据第3节的研究结果可将部分部件的维修周期进行适当调整，优化建议如表5所示。

表5 三级修的优化建议

通过优化调整检修项点及其检修级别，可以达到提高检修体制合理性的目的。

5 结论

本文通过对某型动车组转向架(运行3年)运行数据进行数据筛选，利用统计学原理对转向架各子系统运营过程中的故障数据进行了分析，结合可靠性模型，对转向架及各子系统的故障发生规律及可靠性进行了研究，得出了各子系统可靠性评估指标，建立了可靠性模型。在可靠度为0.9的条件下，针对转向架现有的维修计划，对某些部件进行了维修周期调整，为优化预防性维修提供了参考依据。