大跨弯连续刚构桥自振频率计算公式

2021-08-30韩智强刘世忠周勇军晋民杰王俊霞

太原科技大学学报 2021年4期

韩智强，刘世忠，周勇军，晋民杰，王俊霞

(1.太原科技大学交通与物流学院,太原 030024；2.长安大学公路大型结构安全教育部工程研究中心,西安 710064；3.山西通畅工程勘察设计咨询有限公司,太原 030024)

我国西部属于山岭重丘区，山高谷深，大跨连续刚构桥因良好的线形和空间适应性，在山区公路上逐渐得到广泛应用，而国外较少采用。近年来，常规桥型的动力特性研究都取得了一定进展，文献[1]基于直接模态摄动法推导变截面简支梁动力特性的半解析解；文献[2]研究连续梁桥纵横向自振特性，并提出连续梁桥墩振型函数表达式；文献[3]采用瑞利法推导连续刚构桥纵向振动基频理论解析计算公式。文献[4]基于环境激励的桥梁模态法(UINO法)基础上，提出互功率谱法进行斜拉桥模态参数识别技术；文献[5]从能量平衡角度研究悬索桥颤振的多模态耦合及机理，并推演了各级模态阻尼比的计算方法；这些工作对桥梁动力特性的发展起到很好作用，但对弯连续刚构桥的振动特性，尤其结构纵向振动频率规范[6]还没有相应公式。

本文依据能量法基本理论，采用通用软件ANSYS分析不同曲率半径连续刚构桥一阶纵向频率的变化规律，对比回归分析相应计算公式，研究结果可为大跨弯连续梁桥基频理论计算提供参考。

1 能量法计算桥梁频率

桥梁结构基频通常采用瑞利(Rayleigh)法[7]进行求解，示意图如图1所示：

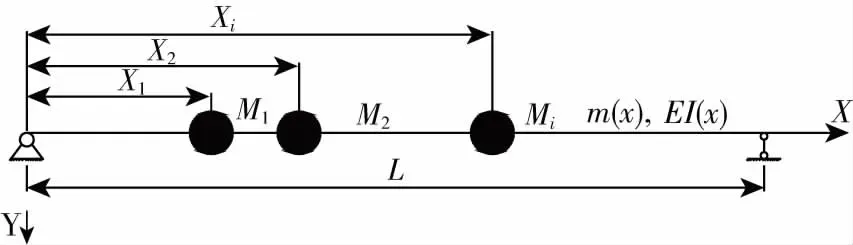
图1 某简支梁示意图

其中：m(x)为简支梁桥单位长度的质量；EI(x)为简支梁桥某一截面的抗弯刚度；Mi为作用在桥面上的第i个集中质量块；xi为第i个集中质量块到桥梁起点的纵向距离；L为桥梁的计算跨径。

结构体系在自振过程中，如果不考虑结构阻尼的作用，结构体系在振动过程中的任一时刻，其动力和势能之和均为一常数，即：

U+V=C

(1)

由式1可知:当结构体系处于平衡条件，即势能为0，动能达到最大，即速度为最大，体系的总能量为：

0+Vmax=C

(2)

当体系的势能为最大时，此时，动能为0，即速度为0，体系总能量为：

Umax+0=C

(3)

根据总能量不变的基本假定，可得式4，即：

Umax=Vmax

(4)

桥梁的横向位移y(x,t)在不考虑简支梁桥阻尼振动的影响，其可由式5表示：

y(x,t)=φ(x)sin(ωt+θ)

(5)

其中:φ(x)为满足梁的位移边界条件的近似振型函数。

梁的动能可表示为：

(6)

梁的位能可表示为：

(7)

因为T+V=Tmax=Vmax，则有：

(8)

即该梁振动的固有频率为[8]：

(9)

2 弯连续刚构桥结构频率计算

2.1 工程简介

本文以某高速大跨弯连续刚构桥为工程背景，桥梁总长241 m，其跨径组合(65 m+108 m+65 m)，主梁标准断面为单箱单室，上部结构混凝土强度为C50，桥梁曲率半径为960 m,桥墩为矩形薄壁空心墩，下部结构为C40混凝土，其总体布置如图2所示。

2.2 弯连续钢构桥基频计算

由于不同曲率半径下弯连续刚构桥截面刚度不尽相同，桥梁结构自振频率也有所区别，为了解其变化规律，以依托工程为基准模型，选取曲率半径范围为(100～1 200)m范围内的桥梁模型，建立24个不同曲率半径的仿真模型(曲率半径间隔50 m)，求解不同曲率半径下桥梁模型的基频值ωi，并与直桥基频值ωj进行比对及拟合，其结果如图3所示。

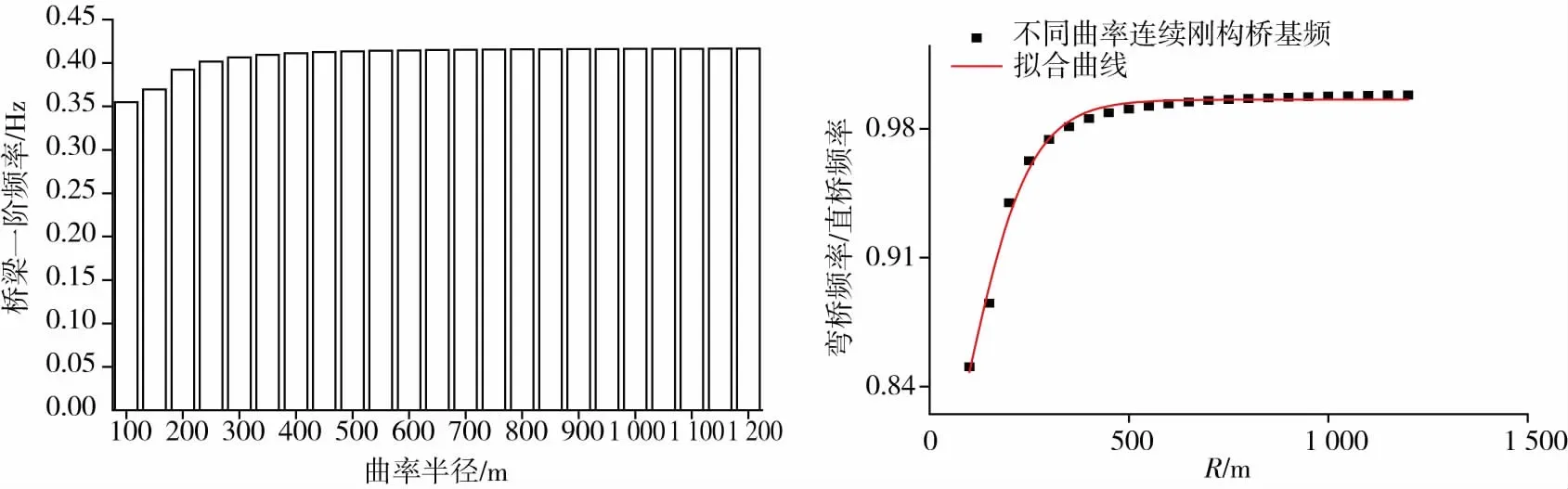
图3 不同曲率半径连续刚构桥基频拟合曲线

通过分析可知：随着桥梁曲率半径变化时，结构基频也相应变化，当曲率半径R<300 m时，随着曲率半径增大，桥梁的基频值增幅较大，当曲率半径R≥300 m时，桥梁基频随曲率半径变化幅度较小，与直连续钢构桥频率值较为接近，通过数值函数拟合，修正弯连续刚构桥频率公式，如式(10)-式(11)所示。

(10)

3 算例分析

为验证公式的适用性，本文以某五跨变截面弯连续刚构桥为试验桥梁，其跨径组合90 m+3×160 m+90 m，桥梁曲率半径R=1 700 m，主梁截面为单箱单室，上部结构采用C50混凝土，墩顶截面高h=9 m，跨中截面高h=3.5 m，下部结构桥墩采用薄壁墩，墩高(46～144)m，如表1所示，下部结构采用C40混凝土[10]。

(1)按照设计图纸进行计算基频值。

(2)本文采用动态测试仪，选取八个样本点进行测定桥梁基频值，如图4所示。

提取样本点基频数据，计算其均值为0.252，方差为0.023 1，如图5所示。

对于算例桥梁，样本数据均位于[μ-3σ，μ+3σ]即[0.183，0.322]区间内，因此，实测基频f1=0.252 Hz，并与理论值进行对比，得出相对误差为4.4%<5%.