改变光栅及其衬底厚度对导模共振传感的影响
2021-08-30李旭峰
赵 星,李旭峰
(1.中煤平朔集团有限公司井工三矿机电管理部,山西 朔州 036002;2.太原科技大学 应用科学学院,太原 030024)
光栅导模共振是入射电磁波经光栅衍射产生的高次谐波与光栅波导之间的耦合共振现象。当光栅内高级次传播波在参数上与光栅波导所支持的导模接近时,光波能量重新分布。由于光栅的周期调制性使得光栅波导有泄漏,因而泄漏波能量也将重新分布,形成导模共振。该导模共振具有衍射效率高、带宽窄等特点,因此在超窄带滤波、光开关以及传感器等方面具有重要的科研价值和发展应用前景[1-3]。1902年自Wood在金属光栅的衍射实验中发现该现象以来[4],涉及相关的理论和实验研究工作已经广泛展开。
导模共振对衍射光栅的结构以及外界环境参量的改变非常敏感,这种改变会导致共振入射角、入射波长、位相以及反射光强等的变化,因此非常适合于光学传感器的应用研究。具备光学传感实时、快速、非接触、非破坏,抗电磁干扰、多通道波分复用以及被检测样品无需特殊处理、免标记等特点。采用位相干涉检测的手段,导模共振的传感灵敏度可获的很大提高[5-6],缺点是系统结构复杂且抗环境干扰能力差,距离商用化仍有一定距离。以金属作为光栅基底,2015年A.Mizutani等人采用严格耦合波法,在固定入射波长(632.8 nm)的前提下,对以金为衬底的光栅灵敏度进行了研究,其结果表明,与介质基底相比,由于金膜的折射率低,从而使得灵敏度相比介质情形提高了2倍多达到~130°/RIU,同时分辨率几乎保持不变[7]。与红外波段相比,在可见光波段工作的光栅导模共振传感器其几何尺寸可进一步的压缩,有利于设计模型的小型化。通过增加光栅周期,导模共振的激励波长产生红移,灵敏度可进一步提高[8]。2020年,崔文丽等人采用有限元仿真模拟,通过介质光栅包覆金属的办法,设计出了角度不明感的导模共振传感器,灵敏度达~600°/RIU[9].相比单面金属波导,2016年马金鱼等人采用双面金属波导结构[10],使得波导区域的功率密度得到提高并同时减小了样品区域的有效折射率,该导模共振传感器的灵敏度可提高一个数量级。2020年采用时域有限差分法讨论光栅周期、占空比、厚度以及组成材料等对导模共振传感的影响也有报道[11],其结果表明,光栅周期对导模共振的传感灵敏度起决定作用,改变光栅占空比以及光栅膜厚也能够对导模共振产生调控,但不论如何三者均是由于产生导模共振的入射角增加的缘故,最终使得该光栅传感器的灵敏度得到了提高。上述文献涉及光栅膜厚的优化研究虽有报道,但在涉及光栅以及光栅基底厚度二者之间的优化设计研究则较少,本文提出的亚波长光栅及其基底厚度改变对导模共振传感的影响正是在此背景下提出来的。
1 仿真模型
图1所示为亚波长光栅的导模共振传感器结构。该结构主要包括三个部分。其一为光栅(组成材料二氧化铬,光学折射率ng=1.98),其周期、刻槽深/宽分别表示为P、hg和wg,光栅的上层覆盖层为待检测液体/气体样品(光学折射率表示为ns);其二是由光栅衬底构成的导波结构与光栅组成为同种材料;其三为最下层的二氧化硅(光学折射率nsub=1.45)衬底。仿真采用宽谱光源(TE偏振,电场方向垂直于纸面)经衬底垂直入射的方式。光栅衍射效率的计算采用严格耦合波分析。严格耦合波法是一种直接有效的电磁场理论,它在光栅区域严格的求解麦克斯韦方程,将麦克斯韦方程的求解问题化为一个求解特征函数的问题,得到光栅区域由特征函数耦合起来的电磁场表达式,然后在光栅区域与其它区域交界面上求解边界条件得到最终衍射效率的值,这种方法一直广泛的使用在各种形状光栅的分析设计中。利用严格耦合波法能够给出光栅衍射效率的解析求解,在此基础上,针对特定衍射条件下的电磁场计算则可采用时域有限差分法(FDTD SOLUTION)来完成。时域有限差分法的基本思想是用中心差商代替场量对时间和空间的一阶偏微商,通过在时域的递推模拟电磁波的传播过程,具有物理作用过程直观明了的特点。仿真计算空间划分网格大小统一为5 nm,该数值远小于入射波长的十分之一,满足收敛条件以确足够的保仿真精度。完全匹配层(PML)至于z方向吸收外向的传输波,x方向则设置为周期边界。
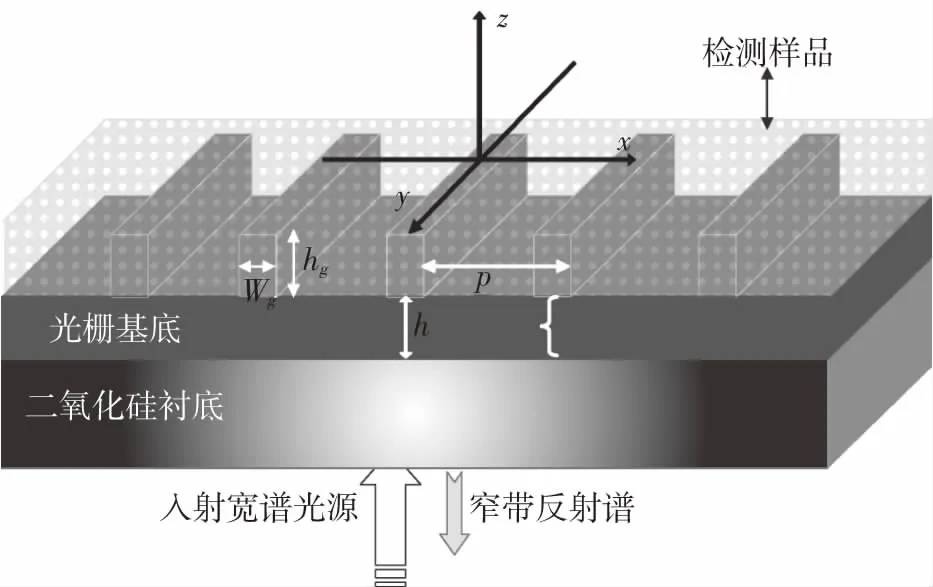
图1 亚波长光栅导模共振传感器结构
2 结果与讨论
导模共振的激励波长主要取决于光栅周期大小,考虑所需样品检测在近红外区间,因此选择周期P=700 nm并设置占空比为f=0.5.取样品折射率为ns=1.3,分别改变光栅及其光栅基底的厚度,得到的反射率图如图2、3所示。由于光栅波导存在截止频率,所以对应图中导模共振的出现需要一定的波长大小。图2中导模共振峰的半高宽(FWHM)受光栅衍射能量损失的缘故,会随光栅厚度的增加而增大,但同时也由于光栅膜厚影响导模共振峰的旁带抑制比,继续增加膜厚,共振峰半高宽反而又得到了一定程度的改善。考虑增加光栅膜厚带来的制作困难,本文中选择的光栅膜厚为hg=50 nm,这样既保证了传感的分辨率得到优化,同时又使得制作相对容易。图3表明随着光栅衬底厚度增加,除导模共振受调制外,同时亦有周期性的背景反射峰、谷出现,根据薄膜干涉理论该现象可由公式(1)给出其物理背景解释。

图2 改变光栅厚度hg=(0~1)um得到的反射率图
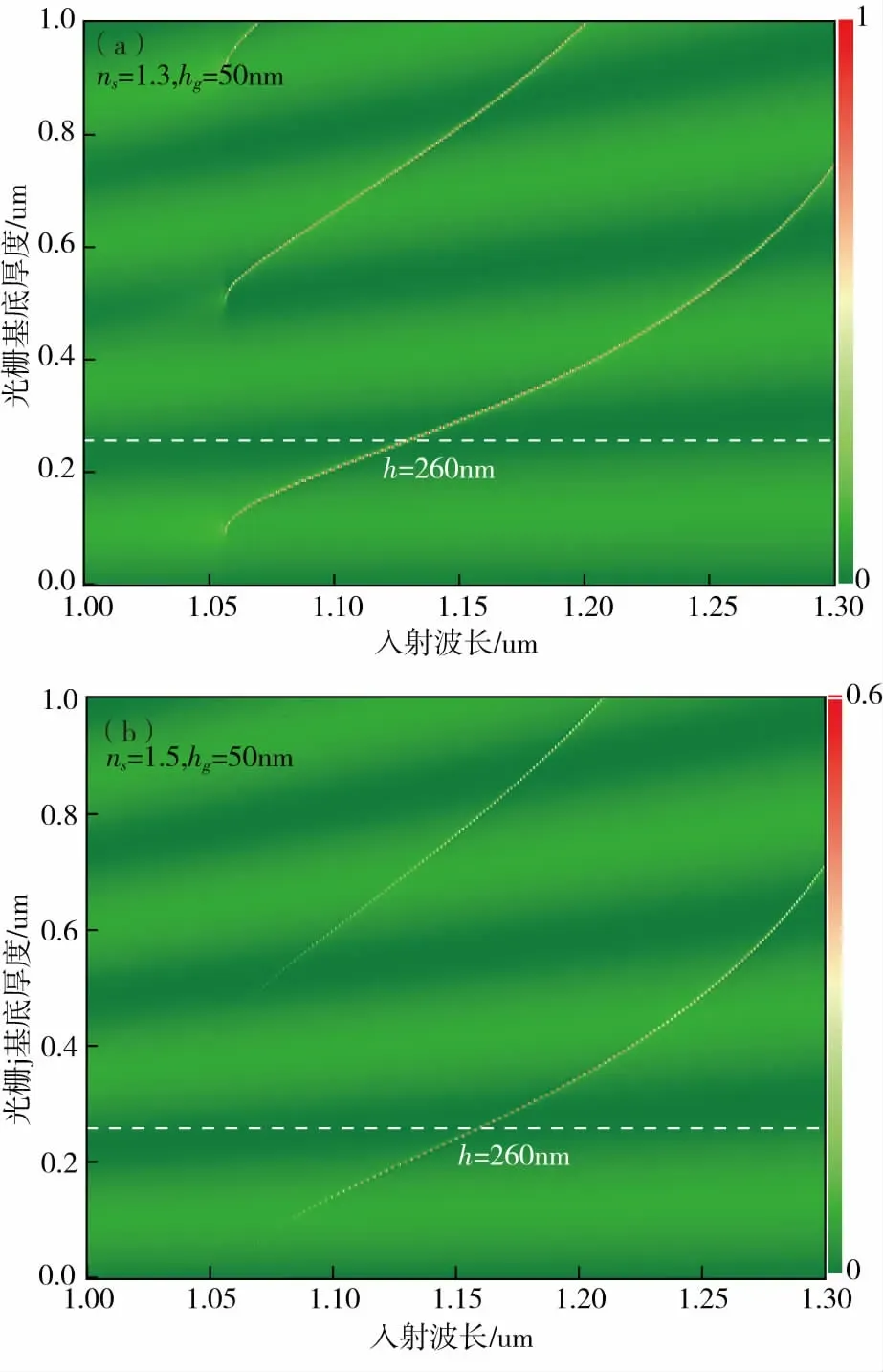
图3 改变光栅基底厚度h=(0~1)um得到的反射率图
入射波由光栅基底进入在其上下面交界面处产生反射,随基底厚度的变化,两反射光束的位相差φ可表示为:
φ=2hngk0+φ1+φ2=n·2π,n=1,2…
(1)
式中φ1,φ2分别表示为上下交界面处的反射波位相改变量,由此可求得光栅基底厚度改变决定的背景反射率变化周期为:
Λ=Δh=λo/2ng
(2)
k0=2π/λ0表示自由空间波矢。该式表明周期仅是入射波长和基底折射率的函数,与被测样品折射率无关,图4计算结果与理论分析符合:给定不同的样品折射率ns=1.3,1.5,计算得出的变化周期相同。为此可通过改变光栅基底的厚度来调节导模共振产生的位置,从而达到改善传感分辨率的目的(见图5).显然如满足公式(2)中n取奇数的条件,此时相应的背景反射为谷(见图4中h=260 nm的情形)。
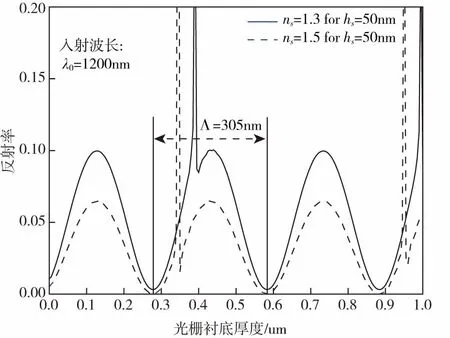
图4 固定入射波长,改变基底厚度h=(0~1)um米得到的反射率

图5 不同光栅基底给出的反射率
定义光栅的等效折射率neff为:
(3)
因为neff
(4)
入射波经光栅衍射,其中第m级衍射波矢沿x和z方向满足:
(5)
由于|kmx|≤(ng2π)/λ0,只能有m=0,±1的情形允许存在。其中零级衍射波不满足导模共振
β/ng=kmx
(6)
的变化条件。对于衍射波m= ±1,在激励波垂直入射的情形下二者处于简并。满足导模共振条件,入射波被耦合到光栅基底波导层中,形成如图6(a)所示的驻波场分布。继续增加光栅基底的厚度,则更为高级次的导模模式被激发出来,见图6(d).固定入射波长,导模共振的产生如图3所示也是周期性的。根据公式(5),可求得改变光栅基底厚度导致导模共振产生的周期为:

图6 导模电场强度分布图
(7)
见图7,仿真结果与理论分析吻合。

图7 导模共振变化周期与入射波长间的关系
增大检测样品折射率,光栅等效折射率增大,进而产生导模共振场的局域性增强,不利于共振辐射,因此获得的反射率降低,共振峰半高宽减小,见图8.以样品折射率ns=1.3的导模共振峰为基准,定义ΔPWV为样品折射率变化量(Δns)对应的共振峰值偏移量,则波长传感灵敏度γ可表示为:

图8 共振波长与检测样品折射率的关系
(8)
设定光谱仪的波长分辨率为δ=0.003[13],则由此获得的该传感器平均灵敏度为:

图9 共振长波长相对偏移量与被检测样品折射率之间的关系
3 结论
在固定光栅组成材料、周期以及占空比的情形下,通过改变光栅及光栅基底的厚度,在对二者参量进行优化的基础上,可以改善导模共振的半高宽以提高传感分辨率。采用浮雕式(光栅膜厚小)光栅结构并通过调整光栅基底厚度,在激发导模共振处于背景反射为极小的位置时,共振峰旁带得到抑制,从而使得传感器的分辨率得到提高;另外由于增加样品折射率导致共振波长增加的缘由,虽然传感的灵敏度提高了,但获得光谱的反射率降低了。本论文的研究可为亚波长光栅在近红外波段传感器的应用设计提供理论参考。
