某型飞机操纵面间隙非线性颤振时域分析

章飞，程芳

（1.中航西飞民用飞机有限责任公司工程技术中心，西安710089）

（2.航空工业第一飞机设计研究院强度设计研究所，西安710089）

0 引 言

现代飞机操纵面驱动系统通常采用伺服控制操纵系统，这种操纵系统是不可逆的。实际上操纵面与不可逆装置之间会有间隙的存在，随着速度的增加，操纵面会发生非线性气动弹性响应，即操纵面发生极限环振荡。这种由于气动和/或结构的非线性影响形成的极限环颤振，不像常见的颤振那样具有破坏性，通常表现为等幅振动，如果其振幅过大，也会影响机体结构完整性，引发结构失效。对于采用不可逆操纵面设计的民用飞机，在适航取证过程中需满足CCAR 25.629“在气动弹性包线内不得出现任何气动弹性不稳定现象”的要求。按照咨询通告AC 25.629-1B第6.3.4节的要求，可以将操纵面间隙的影响等效成操纵刚度的变化来进行颤振分析。

Ni K等、Hu P等基于CFD/CSD耦合技术分析了含有间隙非线性的全动平尾极限环振荡，计算结果与试验数据一致，但是CFD/CSD耦合技术要求建模精度高，同时计算量庞大。描述函数法是从频率域的角度研究非线性控制系统稳定性的一种高效的等效线性化方法，是求解非线性颤振常用的方法。Tang D M等应用描述函数法求解直升机叶片的非线性颤振，将结果和数值计算及试验数据进行了比较，验证了描述函数法解的有效性；陈文等对常用的间隙非线性颤振分析方法的优缺点进行了总结，并提出基于地面共振试验的结果获得等效操纵刚度，使用改进的描述函数法分析得到临界发散速度，其结果与颤振风洞试验结果是一致的，虽然方法可行，计算结果准确，但是不能得到详细的振动特性。目前，行业内对间隙非线性颤振的研究大都基于二元机翼模型，对全机模型的间隙非线性颤振研究鲜见。

本文通过对间隙非线性颤振时域分析方法的研究，以某型民用飞机为例，计算全机带操纵面间隙的极限环振荡结果，分析飞机在不同速度下受扰后操纵面间隙引起的极限环振荡响应历程及特性，并与频域描述函数法计算结果进行对比分析。

1 间隙非线性颤振时域分析方法

考虑典型的中心间隙型非线性环节，如图1所示，其中

α

为偏转角，

M

为回复力矩，

K

为线性操纵刚度，间隙值为2

δ

。在对称间隙区间［-

δ

，

δ

］内，对应操纵刚度为0，操纵面自由旋转；而在该区间外对应线性操纵刚度。该模型可表述为分段线性函数如式（1）所示。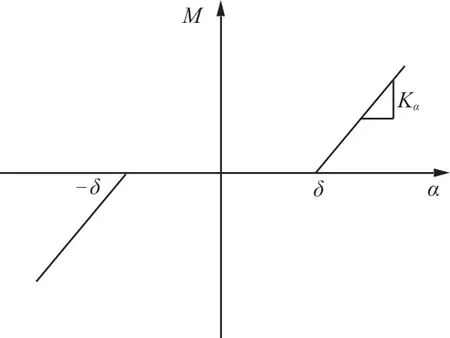

图1 中心间隙型操纵刚度Fig.1 Control stiffness of central freeplay

忽略结构阻尼影响，考虑单个操纵面自由间隙时的结构运动方程如式（2）所示。

式中：

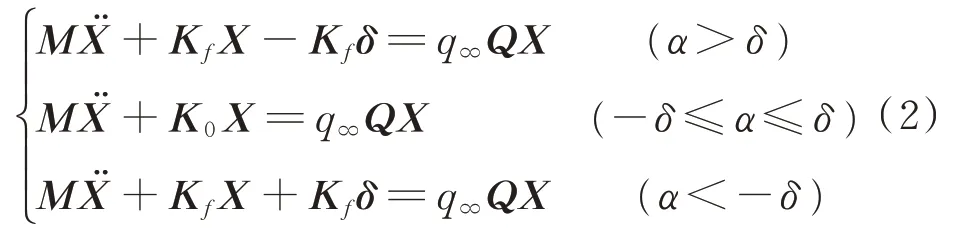
K

为线性情况下的刚度矩阵；

K

为将

K

在操纵面偏转自由度对应的元素置0后的刚度矩阵。

如果考虑两个操纵面同时存在中心型间隙的情况（比如具有对称布局的副翼或升降舵），其结构运动方程如式（4）所示。

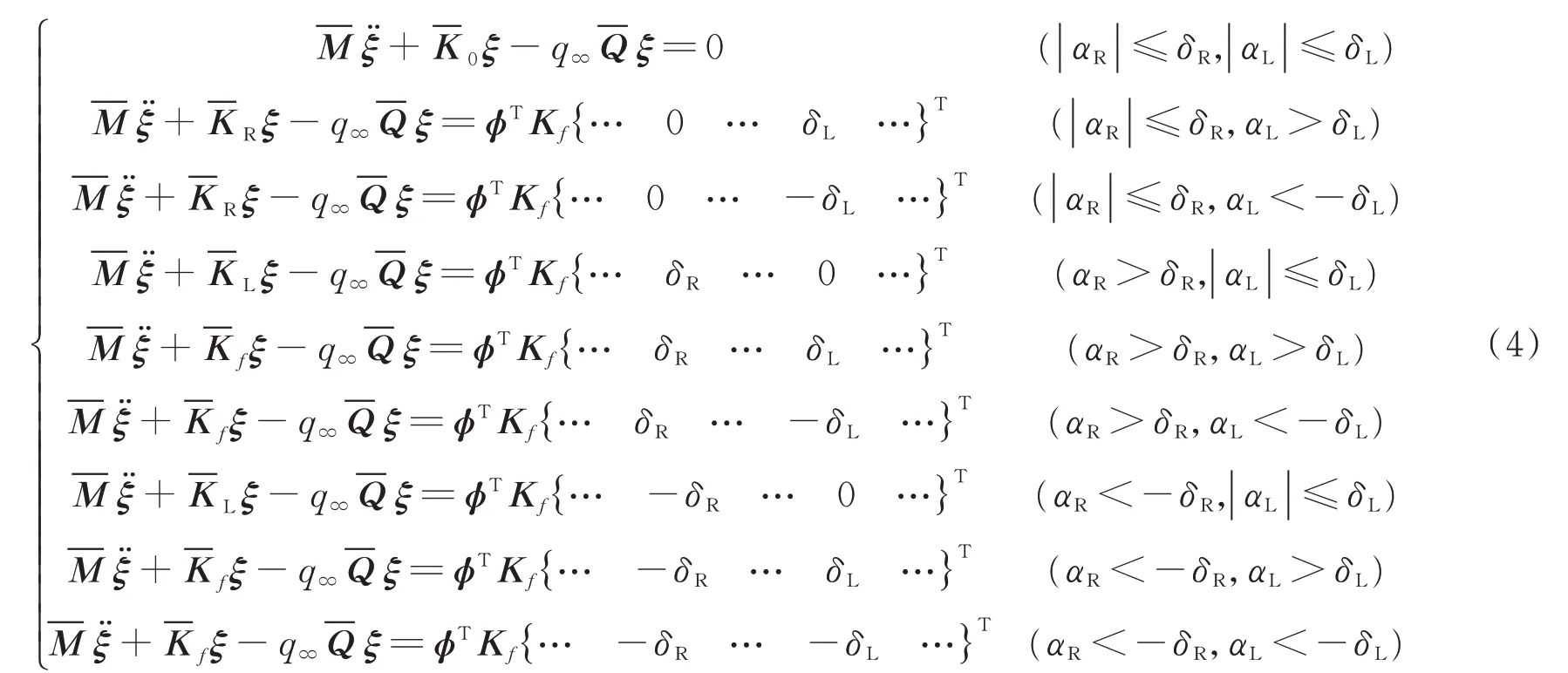
用最小状态法对式（4）的气动力系数矩阵进行有理函数拟合，将频域方程转化成时域状态空间方程，然后进行数值求解。

式中：

s

为拉普拉斯变量；

L

为参考长度；

V

为飞行速度；

A

，

A

，

A

，

D

，

E

为拟合矩阵；

R

为滞后根矩阵。

将频域方程转化成时域状态空间方程：

式中：

X

为气动弹性系统状态变量；

U

为间隙偏移量；

A

和

B

分别为时域空间的系数矩。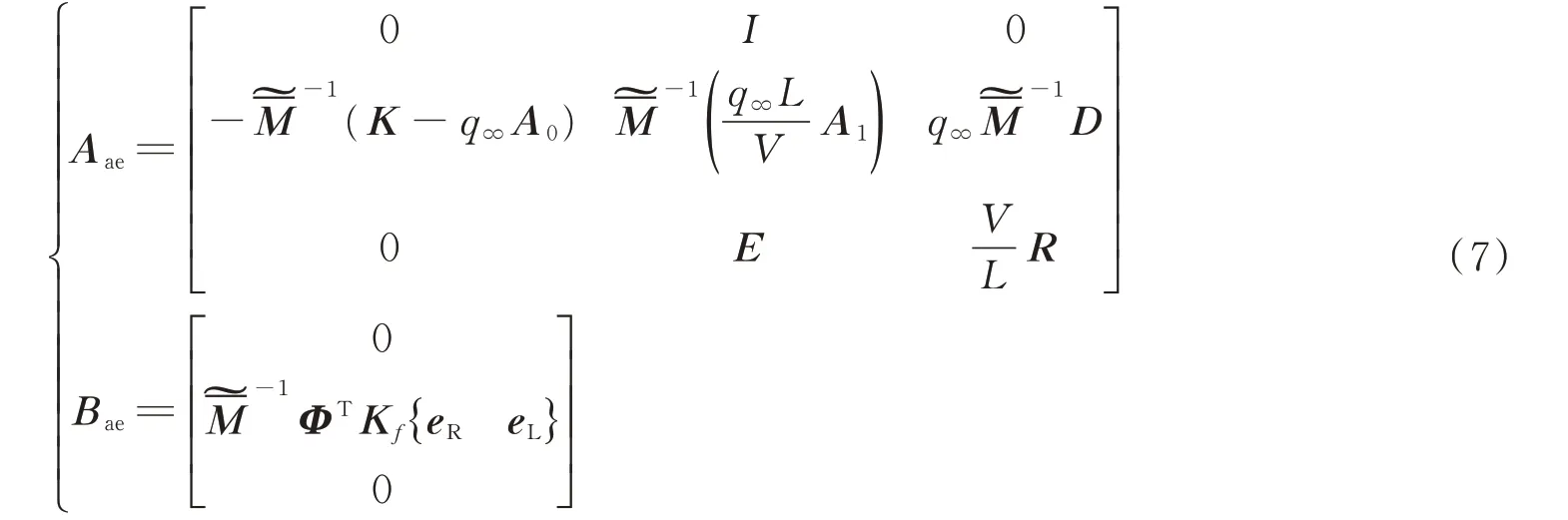

式（6）中的

U

为间 隙 偏移量，根 据式（4）得到：

给方程（6）中的向量

X

施加任意扰动，采用四阶龙格库塔法在时域内求解该方程，可以得到操纵面偏角乃至全机各点位移的响应历程。

2 算例分析

2.1 模 型

以某型民机为例，对于能够准确计算剖面刚心和刚度的部件，如机身、机翼、垂尾、平尾等，直接建立单梁模型；而对于翼身连接区等难以准确计算刚度的区域，采用减缩刚度矩阵的形式来模拟其刚度特性。非定常气动力采用亚声速偶极子格网法模拟，全机气动网格如图2所示，机翼、平尾、垂尾都简化为升力面，机身和发动机简化为细长体和干扰体。

图2 全机气动力模型Fig.2 Aerodynamic model of the entire aircraft

采用软件MD Nastran2010.1进行振动和气动力计算并提取相关质量、刚度和气动力系数矩阵，计算时取海平面空气密度为1.225 kg/m。

2.2 计算结果及分析

本文以升降舵间隙、副翼间隙、方向舵间隙为例进行计算（其中左、右升降舵及左、右副翼考虑具有相同中心型间隙的情形，即

δ

=

δ

=

δ

），计算速度为0~160 m/s。

采用描述函数法计算的间隙非线性颤振特性临界结果与本文时域计算结果对比如表1所示，可以看出：两种方法得出的结果基本一致，针对方向舵间隙两种方法均未出现LCO。

表1 时域/描述函数法计算结果对比Table 1 Results comparison of two methods

本文以升降舵间隙为例对其间隙非线性颤振计算结果展开说明。升降舵无量纲等效刚度系数与无量纲振幅

α

/

δ

之间的关系曲线如图3所示。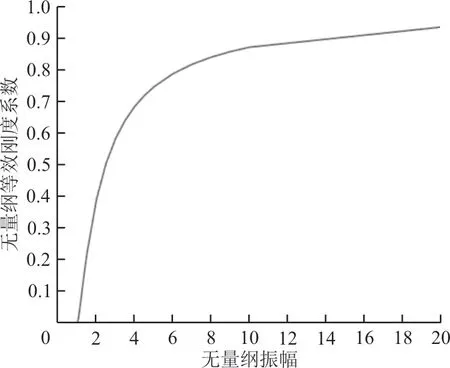

图3 升降舵刚度折减系数曲线Fig.3 Stiffness reduction factor curve of elevator

升降舵无量纲极限环振幅随飞行速度的变化如图4所示。

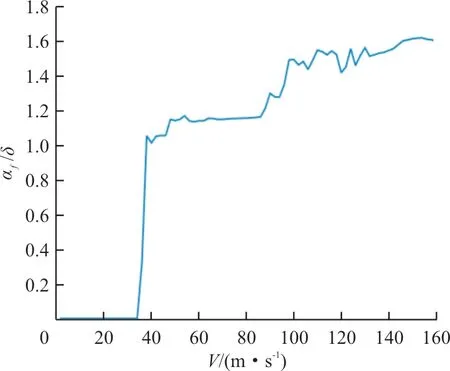
图4 升降舵无量纲极限环振幅随飞行速度变化曲线Fig.4 Curve of LOC amplitude v.s.velocity

升降舵极限环频率随飞行速度的变化如图5所示。

图5 升降舵极限环频率随飞行速度的变化曲线Fig.5 Curve of LCO frequency curve v.s.velocity

典型速度下升降舵无量纲偏角时域响应曲线如图6~图8所示。

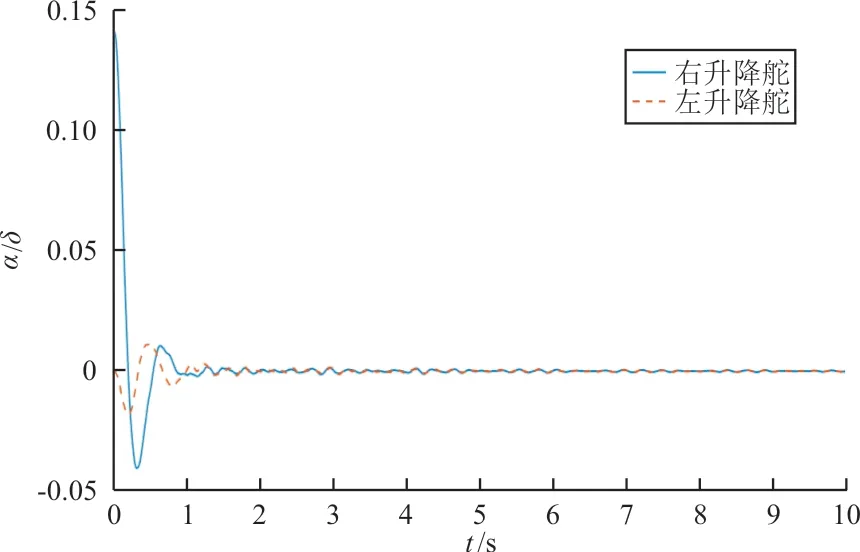
图6 V=20 m/s的升降舵极限环响应曲线Fig.6 Oscillation response history at V=20 m/s

图8 V=40m/s的升降舵极限环响应曲线Fig.8 Oscillation response history at V=40 m/s

图7 V=34 m/s的升降舵极限环响应曲线Fig.7 Oscillation response history at V=34 m/s

从图6~图8可以看出：升降舵从

V

=34 m/s开始出现极限环，极限环频率随速度的增大而增大，在0~

V

速度范围内无量纲极限环幅值不大于1.6。通过频域描述函数法计算的升降舵间隙非线性颤振特性临界结果的

V

-

f

、

V

-

g

图如图9~图10所示。

图9 V-f图Fig.9 V-f curve

图10 V-g图Fig.10 V-g curve

从图9~图10可以看出：时域方法计算的临界颤振速度与频域方法计算结果一致，频域方法对应的无量纲等效参数为0.012。

3 结 论

（1）操纵面间隙非线性颤振时域分析方法能够预测到LCO临界颤振速度，可以直观地得到在飞行包线内操纵面是否有发生极限环振荡的可能。

（2）操纵面间隙时域与频域非线性颤振特性计算结果一致性符合较好，时域分析法可以用于预测操纵面间隙非线性临界颤振速度，在工程中支持民机气动弹性的适航符合性验证工作。