特种工程塑料齿轮的疲劳磨损特性研究
2021-08-29曹晓光马法健杨伟伟
梁 萌,曹晓光,马法健,杨伟伟
(1 国华(河北)新能源有限公司,河北张家口075000 ;2 华锐风电科技(集团)股份有限公司,北京100872 ;3 华锐风电科技(集团)股份有限公司及子公司锐源风能技术有限公司,北京100872)
特种工程塑料有聚醚醚酮(PEEK)、聚苯硫醚(PPS)、聚酰亚胺(PI)等,工程塑料具有耐温耐磨性能好、打印成型率高、质量轻、电绝缘性能好等特点[1]。特别是3D 打印技术已经日臻成熟的今天,高分子聚合材料相关配件在机械系统中的应用被广泛讨论研究。经过3D 打印的特种塑料齿轮,因为成型技术的支持,其齿轮安装结构较为简单,可以实现轮轴一体化设计,排除了各种复杂销键结构和轴套结构带来的轮轴结构复杂性,使系统装配精度更高、系统装配工艺更简单、系统结构成本更低[2]。但高分子聚合材料因为其本身特性,系统刚性低、弹性高、耐热性差,进而在高负荷高扭矩系统中容易发生齿轮疲劳磨损[3]。所以,对特种塑料齿轮的疲劳磨损特性研究对提升其可用性极限有积极意义[4]。
本研究从高分子聚合材料的表面力学、材料力学、工程力学角度入手,对其磨损过程进行数学建模,以实现基于工程逻辑学角度的量化研究,提升相关研究对特种塑料齿轮疲劳磨损过程的研究深度[5]。
1 材料基础特征分析
聚醚醚酮(PEEK)是一种结晶性、不透明、浅灰色的芳香烃类聚合物,属于超耐热型树脂型工程塑料。其耐热性支持最高260℃的工作环境并在此温度条件下保证稳定工况和稳定的力学性能。酸碱反应中,PEEK 可抗除浓硫酸外所有酸碱环境,实现强酸强碱环境中的化学稳定性。当前技术条件下,PEEK 在航空航天、医疗器械、生物食品、电子电工等领域已经得到了较为广泛的应用[6]。
聚苯硫醚(PPS)是一种硫醚官能团优化后的聚苯聚合物,属于刚性工程塑料材料。其刚性超越部分合金材料,具有较高的抗压、抗拉、抗剪性能。且其耐热性能支持最高200℃环境下的长期稳定工况。化学稳定性方面,200℃内未发现可溶解PPS的酸碱溶液环境。PPS多用于电子电气封装材料,在深海钻采系统、汽车系统、电子电工系统中均有应用,也在军工体系中用于导弹、火箭等设施的翼面成型[7]。
聚酰亚胺(PI)是一种包含亚胺环结构的复杂结构高分子聚合物,是极端工作环境中最常用的工程塑料材料。其抗拉强度达到170MPa,超过大部分合金材料。极端温度环境中,PI 可以在-150~600 ℃环境下保持工况。化学稳定性方面,尚未发现可以改变PI 化学稳定性的有机溶剂。PI 多用于航空工业,在卫星等航天器中广泛应用,也在电子封装领域实现了工程普及[8]。
2 材料力学性能模型
2.1 齿轮的接触力学模型
齿轮的接触力学疲劳磨损特征主要来自赫兹(1881年)提出的滚动、静态接触力学模型,该模型中,齿轮的最大剪力并非来自齿轮接触面表面,而是来自齿轮内部。该理论考虑到齿轮接触时的弹性形变和接触面在齿轮啮合边缘的移动过程,且同时考虑到了齿轮啮合部的弹性形变和塑性形变。其模型构成如图1 所示。
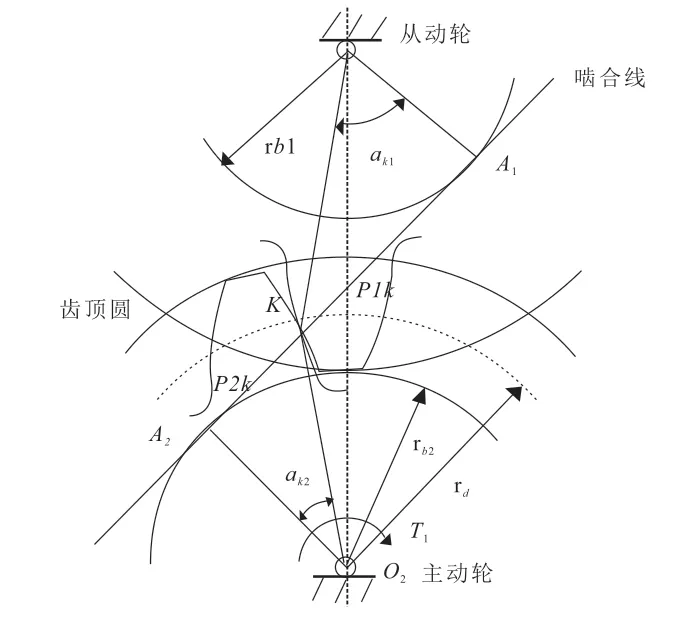
图1 齿轮的接触力学示意图Fig.1 Schematic diagram of gear contact mechanics
图1 中,其最大接触应力 可以表示为公式(1):

式(1)中:F0为齿面啮合力,单位N;L 为齿宽,单位m;E1、E2为两个啮合面对应的两种齿轮材料的弹性模量,单位Pa;μ1、μ2为两个啮合面对应的两种齿轮材料的泊松比;ρ*为齿轮啮合面的综合曲率半径,此处1ρ、2ρ 分别为两个啮合面啮合点处的曲率半径。
2.2 齿轮的弹性力学模型
沃伊特模型是建立在弹性材料弹性形变滞后性特征上的一种齿轮啮合计算常见模型。即弹性材料从受到外力到发生最大弹性形变之间存在一个时间段,且外力撤除到弹性形变恢复之间也存在一个时间段,这一弹性形变滞后过程产生了齿轮系统的运行阻力,进而造成系统抵抗阻力做功,进一步导致能量转化,引起齿轮发热和塑性形变。如图2 所示。
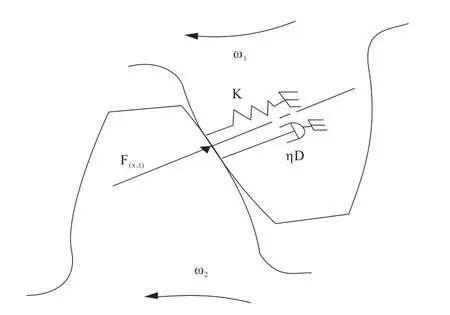
图2 齿轮的弹性力学示意图Fig.2 Elastic mechanics diagram of gear
图2 中,齿轮啮合部的形变滞后性的数学模型表达模式如公式(2):

式(2)中:K 为齿轮啮合部的弹性系数;ηD为齿轮啮合部的粘度;W 为作用力F(*) 条件下的啮合部齿宽变形量;B 为啮合点的等效齿宽;F(x,t)为作用力F(*)在时间轴t 上的周期变化函数。
2.3 两种力学模型的整合
因为齿轮啮合转动的工程结构特殊性,其作用力变化周期符合三角函数的周期规律,且赫兹应力滞后于啮合力,所以,其周期函数可以写做公式(3):
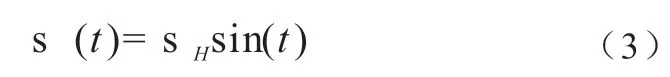
将公式(1)的赫兹模型理论代入公式(3),可得公式(4):
式(4)中:x1为啮合点到齿轮物理中心的法线距离;b(t) 为啮合点等效齿半宽;σH(t)为最大接触应力的时间变化函数。
综合考虑两种齿轮应力模型,可以得到其积分函数,如公式(5):
此时,假定 F(x,t)=F0(x)s inkt,那么其最终工程力学方程可以写做公式(6):

式(6)中:*E 表达式可根据赫兹模型写做公式(7);其他数学符号含义同上。

3 齿轮的磨损模型及其寿命分析
基于特种工程塑料的齿轮结构与基于合金材料的齿轮结构一样,在投入运行的初始阶段,存在一个快速磨损期,即俗称的跑合期或称为磨合期,之后是一段相对稳定的慢速磨损过程,为齿轮结构的正常工作期,正常工作期后,即齿轮结构的磨损体积超过V2 后,再次进入到快速磨损的阶段,即磨损失稳期,又称报废期。其磨损过程如图3 所示。

图3 齿轮磨损过程示意图Fig.3 Schematic diagram of gear wear process
图3 定义的磨损过程结合前文分析的齿轮运行工程力学模型,可以构建齿轮磨损系数模型,其表达式可写做公式(8):

式(8)中:K为齿轮的磨损系数,在该模型中,主要为摩擦力做功热转化过程的热仿真模型架构;V为常规工况下的磨损体积;H为齿轮结构的维氏硬度;F为齿轮的受理载荷;L为常规工况下的摩擦行程;v为齿轮啮合过程的相对滑动速度;t为齿轮的工作寿命;h为齿轮的最大容许磨损深度;σH为齿轮啮合过程的最大接触应力。
公式(8)中的F、v值均为周期变化值,h值为随机变化值。假定T为系统主动轮的加载扭矩,ra为分度圆半径,b为齿宽,此时F可写做F=T/rab;假定r为齿轮等效半径;n为齿轮转速,则v可写做v=2π rn/60;针对h值的磨损量控制,假定系统容许的最大法线磨损量为[h],那么必然有h≤[h];所以,整合上述参数,将公式(8)中的齿轮寿命t进行提取,可以得到公式(9):

式(9)中:K*=K∙Tm,Tm为齿轮摩擦的热动力系数。
4 工程塑料齿轮的有限元仿真分析
4.1 有限元模型的建立
在SolidWorks 及GearTrax 系统中构建齿轮3D 几何模型,传动比为1:1,两个齿轮采用相同材料和相同规格进行设计,以排除传动比、扭矩比等其他因素对工程塑料齿轮磨损过程和寿命演化的影响。其齿轮参数见表1。

表1 齿轮模型参数表Table 1 Gear model parameters
网格划分过程使用Contact Sizing 控件,重点加强齿上网格密度,稀疏其他区域网格密度,每齿轮总单元数量设定为174880 个,每齿轮总节点数设定为206288个,上述3D 模型经网格划分后的实际效果如图4 所示。

图4 有限元网格划分示意图Fig.4 Schematic diagram of finite element mesh generation
在高温摩擦试验机上测定被测试材料的摩擦稀疏,测试材料为聚醚醚酮(PEEK),表面粗糙度Ra 处于0.20~0.80μm,实验参数为:摩擦载荷200N、实验转速200r/min;摩擦升温20℃;实验周期3600s。
此时对实验中产生的摩擦系数机器辅助记录过程进行录波,其录波图结果如图5 所示。图5 中,滑动摩擦系数的测定结果,稳定在0.27~0.36 之间。

图5 摩擦稀疏测定结果图Fig.5 Results of friction sparsity measurement
对聚醚醚酮(PEEK)的相关材料特性进行文献考证和实验读取,得到其弹性模量为3.55×109Pa;泊松比为0.4;热传导率为0.25Wm-1K-1;热膨胀系数为4.7×10-5;比热容为1330Jkg-1K-1;材料密度为1.32gcm-3。在SolidWorks 及GearTrax 系统中,选 择ASTS 摩擦类型,静摩擦系数设定0.10,动摩擦系数设定为0.34,驱动转速500r/min,从动轴施加负载扭矩20Nm。在此基础上进行有限元仿真试验。
4.2 齿轮啮合面温度有限元仿真结果
因为前文分析中发现,固定材料构成条件下,影响齿轮材料磨损的核心变量为齿轮的表面温度。所以,首先对齿轮的传动过程进行温度变化的瞬时仿真。该温度变化的原理是啮合点导致齿轮弹性形变带来的做功热转化效应。其有限元分析结果如图6 所示。
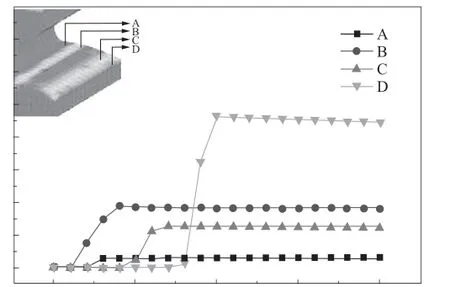
图6 瞬时升温仿真结果Fig.6 Simulation results of instantaneous temperature rise
图6 中发现,齿轮齿根部的瞬时升温效应最低,而齿尖部的瞬时升温效应最高。即可认为,齿轮齿尖部的磨损过程是导致齿轮磨损的最重要诱因。对整个啮合面的温度瞬时变化情况进行分析,得到图7。
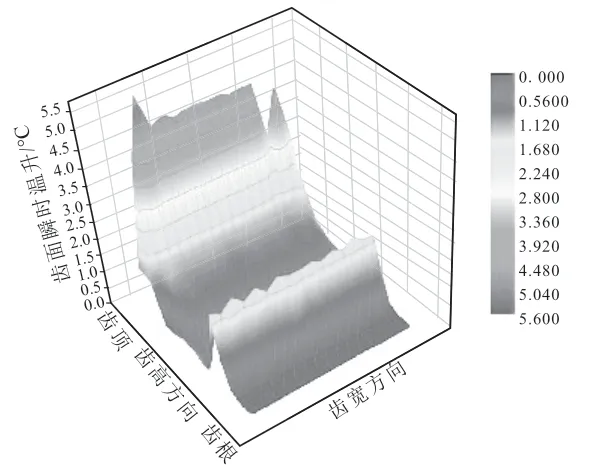
图7 齿面啮合过程瞬时升温等温线图Fig.7 Isotherm diagram of instantaneous temperature rise during tooth surface meshing
图7 中,瞬时升温超过3.0℃的区域,全部集中在齿尖部。齿中部局部隆起部分可能发生1.6℃以上的瞬时升温,但该升温区域的升温效应显著低于齿尖部。其他区域的瞬时升温在0.5℃以下。可见齿轮的传动做功部位主要集中在齿尖部,其次为齿中部[9]。
对齿轮啮合面的升温时间周期进行测定,可以得到表2。

表2 瞬时升温至最高温度的时间周期测定结果表(单位:s)Table 2 Measurement results of time period from instantaneous heating to maximum temperature
表2 中转速越低、扭矩越大,其升温周期越长,根据前文的数学模型分析,此时齿轮受到的磨损强度越大。反之,齿轮的升温周期越短、磨损强度越小。即齿轮运行在高转速低扭矩的情况下,有助于减弱齿轮啮合面的升温效应,减轻磨损[10]。
4.3 齿轮使用寿命的有限元仿真结果
真实工况条件下,影响齿轮磨损和齿轮寿命的因素较为复杂,而本研究是在理想数学模型的基础上构建有限元模型对其寿命进行分析,即该有限元仿真结果是理想状态下的齿轮理论寿命,且该模拟同样根据聚醚醚酮(PEEK)材料构建的齿轮展开。其仿真结果见表3。

表3 齿轮理论寿命分布表(单位:h)Table 3 Theoretical life distribution of gears
表3 中,在30 齿模数2.0的1:1 传动比PEEK 齿轮系统中,在1Nm 扭矩和50r/min 转速条件下,齿轮的理论寿命超过700h,但其他工况条件下,齿轮寿命显著降低,如果要保持100h 以上的齿轮理论寿命,在20Nm 扭矩条件下,齿轮转速不能超过50r/min 转速,在1Nm 扭矩条件下,齿轮转速不能超过1000r/min。即齿轮寿命在低扭矩低转速条件下更长。
5 总结
通过在数学模型下对PEEK 齿轮进行进行有限元建模分析,发现在摩擦温度控制层面,较高转速和较低扭矩条件下,齿轮的升温时间最短,在较低转速和较低扭矩条件下,齿轮的理论寿命最长。即在进行特种塑料齿轮系统设计中,应该最大限度降低齿轮的工作扭矩,以实现稳定的齿轮工况,延长齿轮的理论寿命。
