顾及季节变化的西南地区大气加权平均温度模型

2021-08-29郑磊

导航定位学报 2021年4期

郑磊

（西南交通大学希望学院，成都 610000）

0 引言

全球卫星导航系统（global navigation satellite system,GNSS）的快速发展为GNSS 气象学的出现奠定了基础。GNSS 气象学是借助地基GNSS 观测数据探测大气可降水量（precipitable water vapor,PWV）的一种探测技术，该技术的出现解决了传统水汽探测技术时空分辨率较低、成本昂贵、技术难度大且复杂的问题，可为气象与灾害监测等相关部门提供高精度、范围广、实时的水汽分布数据，是目前气象部门监测天气和气候变化的重要手段之一[1-4]。基于GNSS 数据探测水汽的过程中，大气加权平均温度模型Tm是计算大气可降水含量的关键参数，模型的精度直接影响反演大气可降水含量的误差[5]。

Tm信息可以通过探空资料或大气再分析资料计算获得，其缺点是不能实时获取任意位置处的Tm值。为了能够实时获取Tm信息，通常需要建立一个高精度的Tm模型。文献[6]首次提出了大气加权平均温度Tm与地表温度Ts的线性回归模型。文献[7-11]借助欧洲中期天气预报中心（European Centre For Medium-Range Weather Forecasts,ECMWF）数据、全球无线电探空（integrated global radiosonde archive,IGRA）数据和气象、电离层、气候卫星探测系统（constellation observing system for meteorology、ionosphere and climate,COSMIC）数据建立Tm与地表气象参数的全球分区线性模型、单因子模型、多因子模型等。这些模型具有良好的Tm计算性能，但依赖于实测的气象参数，从而限制了它们在实时GNSS 水汽监测中的应用。为了解决上述问题，须构建一个非气象参数的Tm经验模型，以满足GNSS 水汽的实时计算[12]。文献[13-16]建立了中国低纬度地区、长三角地区、吉林、青岛本地化Tm模型，实验结果表明这一系列经验Tm模型在一定程度上可以提高GNSS 水汽的精度和可靠性，在各自范围内均表现出各自的优越性。尽管目前建立了一系列各自地区的Tm模型，但在西南地区高精度的实时Tm模型依然缺乏，从而限制了GNSS 气象学技术在我国西南地区的发展和应用。西南地区以盆地、丘陵地形为主，四周均是高山峻岭，获取探空数据困难且时空分辨率较低。近年来，中国大陆构造环境监测网络（crustal movement observation network of China,CMONOC）及各省市连续运行参考站（continuously operating reference stations,CORS）的快速发展已经积累了大量长期运行的GNSS 观测数据；因此，迫切需要构建中国西南地区高精度、实时的Tm模型，为GNSS 气象学在西南地区的应用奠定基础。本文基于地基GNSS 观测数据和探空站数据构建顾及季节变化的西南地区大气加权平均温度模型，并对模型精度进行评估。

1 数据处理理论与方法

1.1Tm 计算方法

利用数值积分法获取的Tm具有精度高、易实现，受气象元素引起的误差综合影响小的优点，因此在建立西南地区本地化Tm模型时将数值积分法计算的Tm作为真值。将测站上空的水汽压和绝对气温沿天顶方向进行积分[14]，可表示为

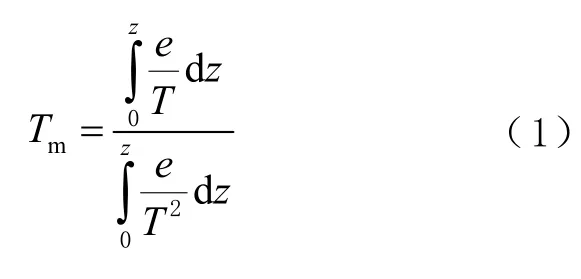
式中：e为水汽压，单位为hPa；T为绝对温度，单位为K；z为相邻气压层之间的厚度，单位为m；Tm为大气加权平均温度，单位为K。由于水汽压是间接求解的，根据温度计算水汽压的公式为：

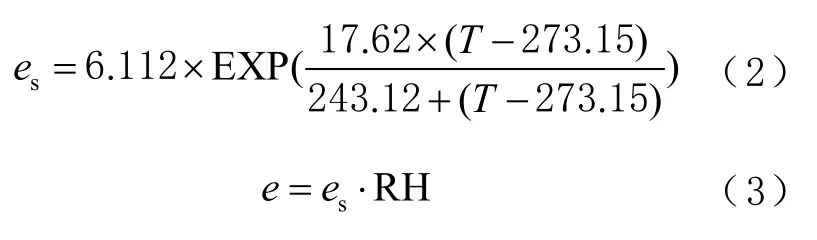
式中：T为当前气压层的温度，单位为K；es为饱和水汽压，单位为hPa；RH 为相对湿度。

或根据比湿计算水汽压，其表达式为

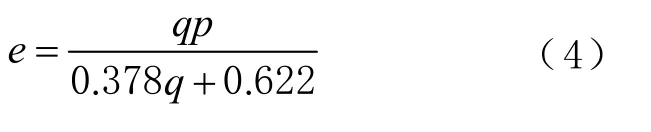
式中：q为湿空气中水汽质量与总湿空气的质量之比；p为当前层的气压，单位为hPa。

1.2 地基GNSS 计算PWV基本原理

基于GNSS 观测数据和气象数据可以获取对流层天顶总延迟、天顶静力学延迟（zenith hydrostatic delay,ZHD），其计算公式[3]为

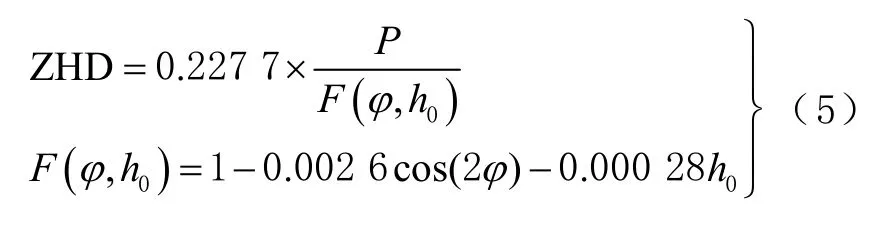
式中：φ为测站的纬度；h0为测站海拔高度，单位为km；P为测站地面气压，单位为hPa。天顶对流层延迟减去天顶干延迟 ZHD 得到天顶湿延迟ZWD，即有

再利用贝维斯（Bevis）模型计算出加权平均温度Tm，进而得到水汽转换系数Π。天顶湿延迟与水汽转换系数相乘即可得到大气可降水量PWV，即有式中Π是无量纲转换因子。在此Π取经验值为0.15[15-16]，证实了Tm是影响PWV 精度的关键参数之一。

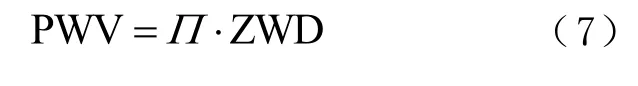
2 实验与结果分析

2.1 数据来源

本次实验过程中选取西南地区2017—2019 年探空数据和地基观测数据，主要包括气压、高度、温度、露点温度等参数，其中GNSS 站点分布如图1所示。探空数据由美国怀俄明州立大学提供，地基数据由中国地震局GNSS 数据产品服务平台提供[14]。

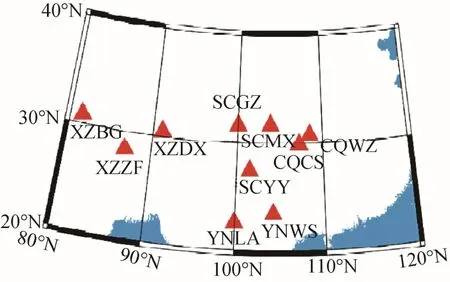
图1 GNSS 站点分布

2.2 顾及季节变化的大气加权平均温度模型案例分析

2.2.1 Tm 影响因子相关性分析

基于地基GNSS 水汽遥感研究表明[14-15]，大气加权平均温度模型Tm与地面温度Ts、水汽压es的自然对数和地面大气压Ps之间存在一定的相关性。对Tm与Ts、es、Ps进行相关性分析的结果如图2所示。

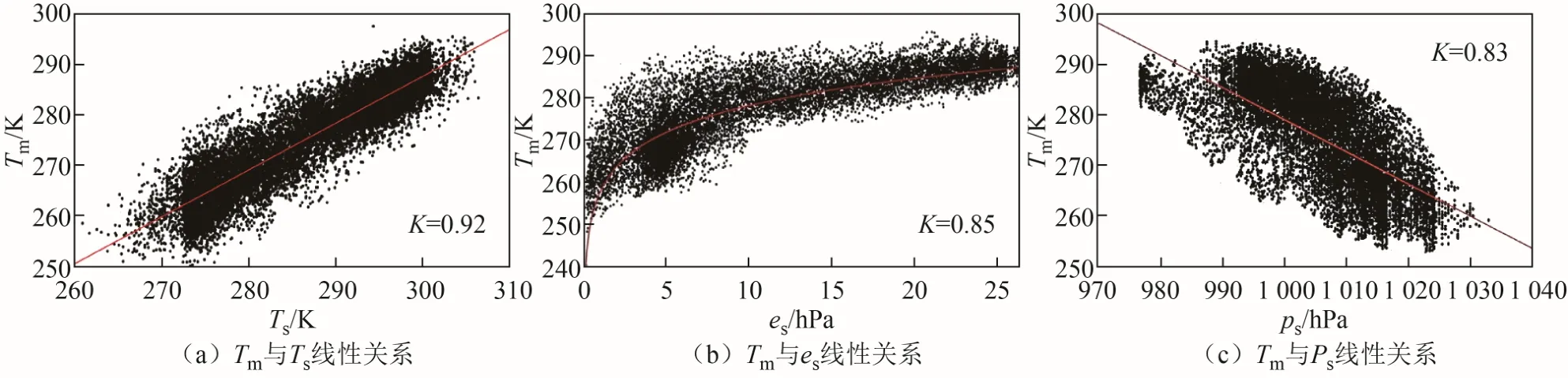
图2 影响因子线性关系

由图可知，Tm与Ts、es、Ps之间都具备较强的相关性，Tm与Ts、es呈正相关，与Ps呈负相关，其相关系数K分别是0.92、0.85、-0.83。根据式（1），随着温度的增加，Tm值会增加，而当温度保持不变时，随着水汽压的增加，Tm值会增加，因此Tm与Ts、es呈正相关；当大气压增加时，温度会降低，温度降低导致Tm值减小，因此Tm与ps呈负相关。

2.2.2 建立顾及季节变化的大气加权平均温度模型

在建立西南地区大气加权平均温度模型Tm过程中，考虑到加权平均温度的季节变化特征明显，将2017—2019 年的气象参数和加权平均温度总样本按照季节进行分类，分别建立单因子、双因子、多因子年模型和季节性模型。

1）单因子：基于Tm与Ts间的相关性，对其进行一元线性拟合，即得到西南地区顾及季节变化的单因子模型，设线性方程为

2）双因子：对西南地区Tm、es、ps数据进行二元线性拟合，即可得到西南地区顾及季节变化的双因子模型，设线性方程为

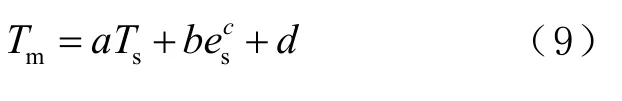
3）多因子：根据西南地区Tm与Ts、es、Ps间的相关性，对其进行多元线性拟合，即可得到西南地区顾及季节变化的多因子模型，设线性方法为

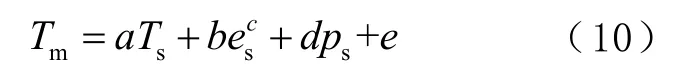
式中a、b、c、d、e 均表示常数。建立的西南地区顾及季节变化的单因子、双因子、多因子模型如表1 所示。

表1 单因子、双因子、多因子年模型和季节性模型

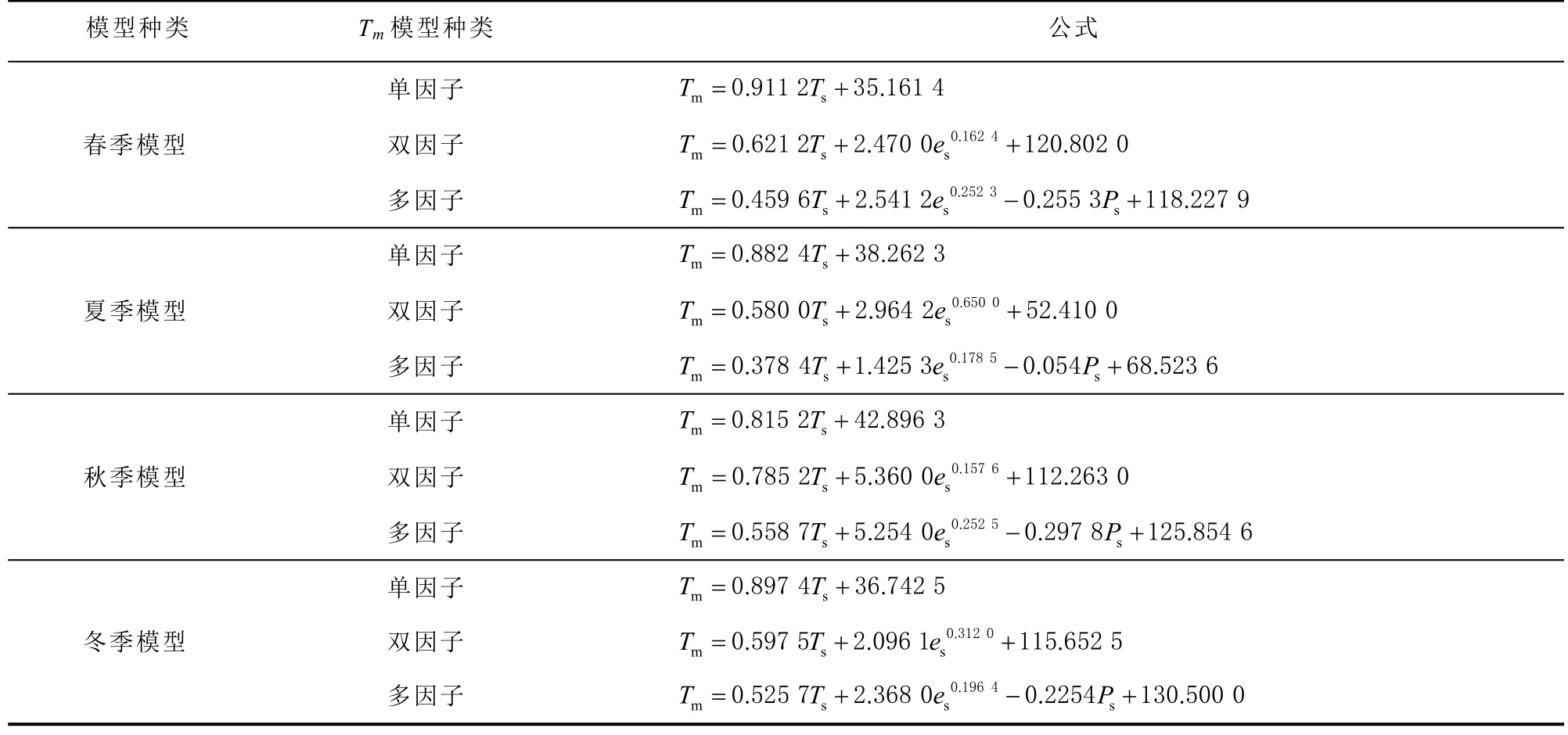
（续）

2.2.3 Tm 模型精度评估

为了评估建立西南地区顾及季节变化的Tm模型的精度，使用平均偏差Sbia值表示Bevis 模型和本地化Tm模型分别与参考值之间的偏离程度，使用标准差Dst值和均方根误差Srm值表示Bevis 模型和本地化Tm模型与参考值间的离散程度。Sbia、Dst和Srm值越小，表明模型精度越高，Sbia、Dst和Srm值越大，模型精度越低。计算公式[17]分别为：

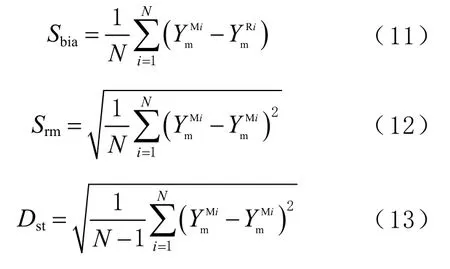
式中：N为样本数量；为模型计算值；为参考值。分别对精度因子进行统计，其结果如表2 所示。

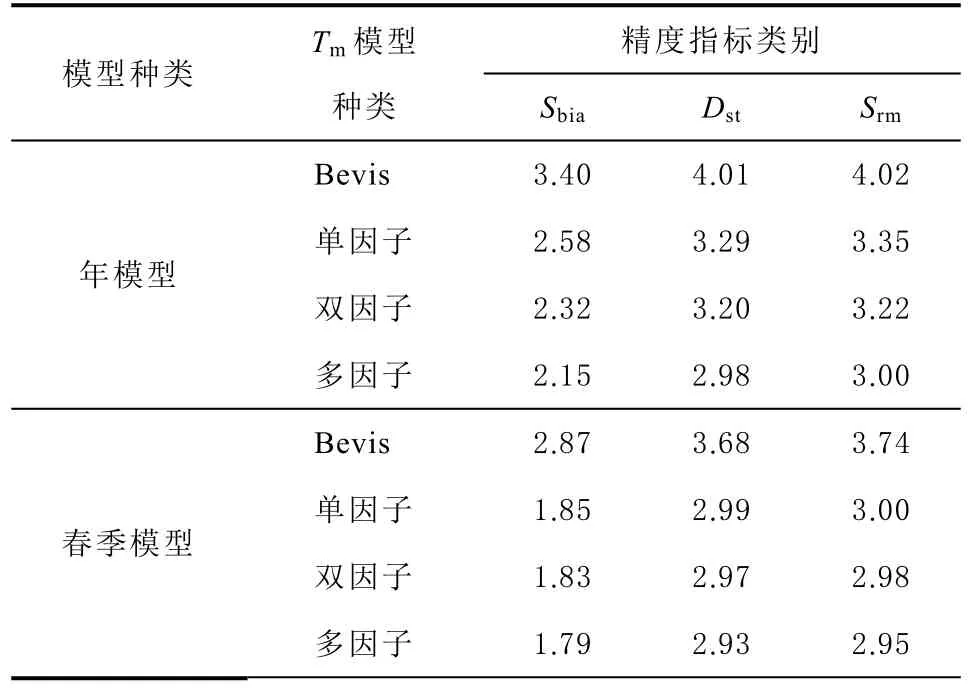
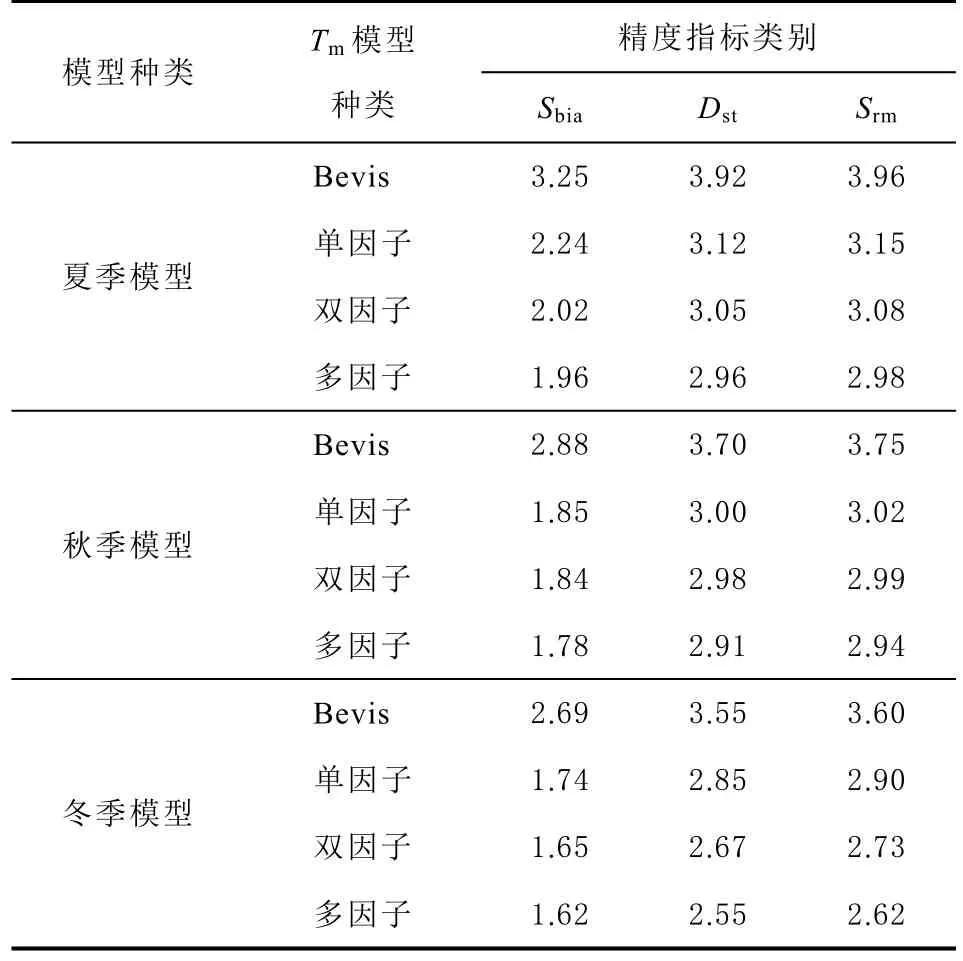
表2 不同Tm 模型的精度分析 K

（续）

由表可知：分季节建立的Tm模型比年Tm模型精度要高，春秋二季模型精度相差不大，夏季精度表现为最差，冬季模型的优越性表现最为突出，分析其原因可能是由于冬季雨水天气较少，使得Ts、es、Ps等因子成为必不可少的因素；年和季节单因子、双因子、多因子Tm模型精度均优于Bevis 模型，且多因子模型精度优于双因子模型，双因子模型精度优于单因子模型。总体而言，顾及季节变化的多因子模型可以更加准确地获取西南地区Tm与PWV 信息。

2.2.4 PWV 精度评估

建立西南地区顾及季节变化的Tm模型是为提高GNSS 水汽反演的精度，将探空数据作为参考值，统计Bevis 模型和顾及季节变化Tm模型计算的PWV 值，再分别与参考值进行对比分析，忽略因地基GNSS 站与探空站在地理位置上的不同而引起的PWV 在数值上表现出来的细小差异。统计结果如表3 所示。同时给出了2018 年CQCS 站和XZBG 站的PWV 偏差图（分别代表Bevis 模型和顾及季节多因子模型的最大偏差区间），分别如图3、图4 所示。

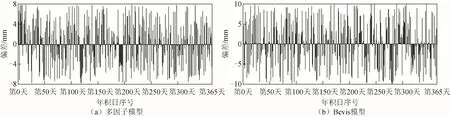
图3 XZBG 站PWV的偏差

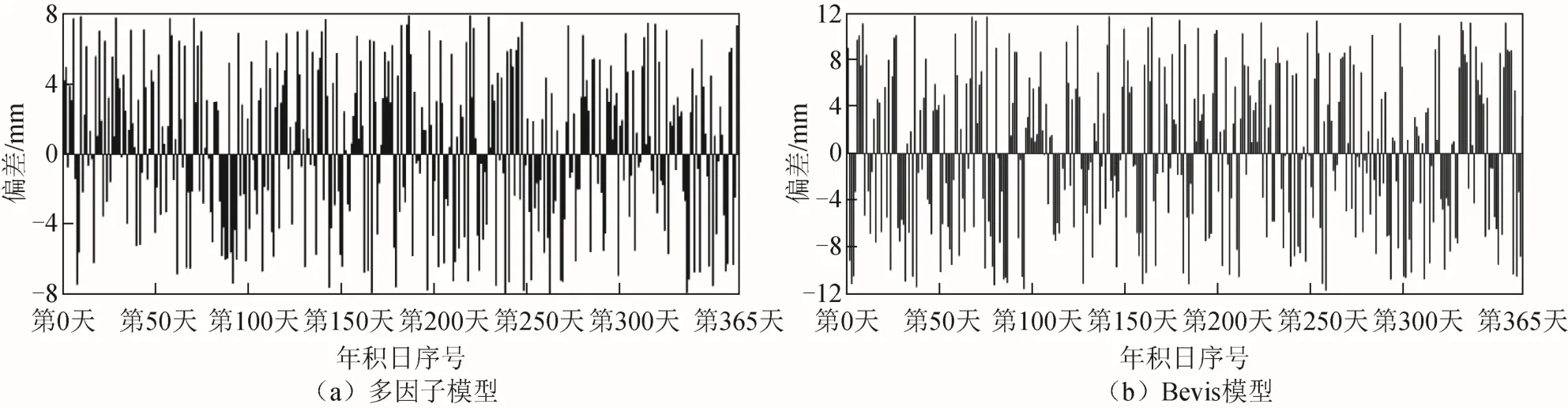
图4 CQCS 站PWV的偏差

由表3 可以看出：同一测站Bevis 模型与参考值之间的PWV 偏差均大于顾及季节多因子模型与参考值之间的PWV 偏差；Bevis 模型的最大偏差区间是[-12 12]，顾及季节多因子模型最大偏差区间是[-8 8]。

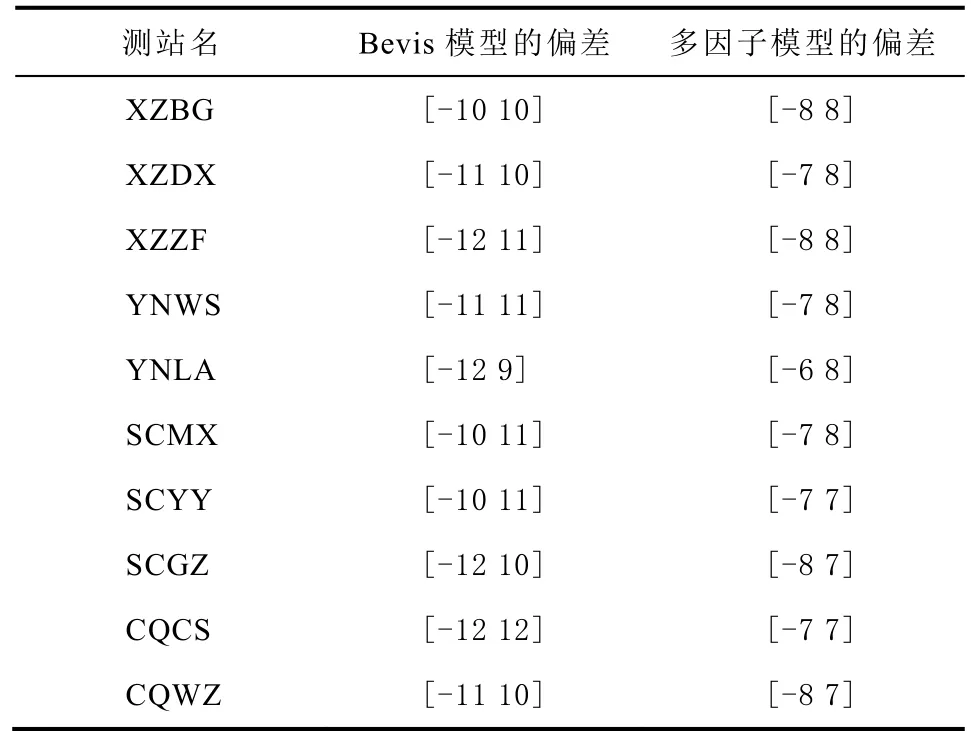
表3 不同模型与参考值之间的PWV 偏差区间 mm

从图3 和图4 可以清晰看出，XZBG 站和CQCS站基于顾及季节多因子模型反演PWV的偏差位于区间[-8 8]，XZBG 站和CQCS 站基于Bevis模型反演PWV的偏差分别位于区间[-10 10]和[-12 12]，表明西南地区顾及季节变化多因子模型比Bevis 模型偏差更小、精度更高，可以提供更为精准的PWV。