高速铁路GNSS 框架控制网平差基准一致性检验

王剑辉，尹 彤，赵有兵，张 莹，李旭洋

（1.广东省地质测绘院，广州 510800；2.自然资源部 测绘标准化研究所，西安 710054；3.中铁二院工程集团有限责任公司，成都 610031；4.自然资源部 第一地形测量队，西安 710054）

0 引言

高速铁路框架控制网（high-speed railway frame control network,CP0）应在初测前采用全球卫星导航系统（global navigation satellite system,GNSS）测量方法建立空间3 维（3D）控制网，全线一次性布网，统一测量，整体平差，作为全线（段）的平面坐标框架基准[1]。CP0 外业测量时，应联测国家A 级、B 级GNSS 控制网或国际GNSS 服务组织（International GNSS Service,IGS）连续运行参考站等高等级已知点进行整网基线解算和平差计算。

我国目前使用的坐标系统为2000 国家大地坐标系（China geodetic coordinate system 2000,CGCS2000），其坐标框架为国际地球参考框架1997（international terrestrial reference frame,ITRF1997），历元为2 000.0。其起始历元至今已跨度二十余年，由于亚欧板块的绝对运动及内部子板块的相对运动，CGCS2000的很多框架点位置已经发生较大变化。所以在CP0 与CGCS2000 框架点或 IGS 站联测时，大跨度的高等级点的CGCS2000 坐标跟其当前历元坐标是否具有一致性，是确保基准稳定的关键。为了避免将基准误差带入平差结果中去，必须提前对高等级已知点进行一致性验证。为此，本文研究赫尔默特（Helmert）模型算法，并使用Helmert 法对高等级已知点稳定性进行一致性检验，探测并剔除有问题的高等级已知点，以避免在CP0的解算中引入基准误差，从而得到更为精确的坐标。

1 基准一致性检验方法

Helmert 法能够计算输入坐标集到参考坐标集的变换参数，从而体现出2 套坐标集之间在平移、尺度、定向等方面的相关变化特性[2]，并通过转换后的残差探测和定位异常坐标点。Helmert 模型主要是通过对2 套坐标集进行对比，通过2 套坐标集公用点求取Helmert 模型7 参数，即3 个平移参数、3 个旋转参数和1 个比例因子[3]，并按照7 参数将检验坐标系坐标转化到参考坐标下。该模型建立的前提是承认这2 套系统的质量重心是一致的[4]。采用最小二乘约束平差方法，将2 套坐标的差异导入Helmert 模型，然后采用参数平差模型，最终估计出Helmert 参数，同时求取坐标残差[5]。

对于比较大型的区域或全球网络的坐标，则应采用空间直角坐标（X，Y，Z）形式。在这种情况下，估计的Helmert 转换参数是指地心笛卡尔坐标系。该坐标系下的转换模型为

式中：Xlarge-0为大区域的参考坐标矩阵；Xlarge为大区域的输入坐标矩阵；X0为平移向量矩阵；Ri(ri)为是绕i轴的旋转角度ri的旋转矩阵，i=x、y、z；k为缩放参数。

对于地方网络和小区域网络，适合采用测站空间直角坐标（N，E，U）形式，则估计的变换参数将引用以输入坐标集重心（质量中心）为原点的局部地平系统。输入坐标集的重心计算公式为

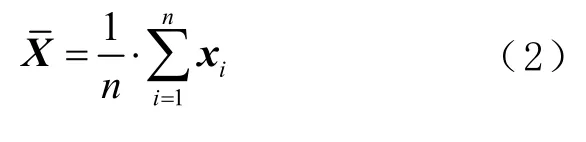
借助于重心X的椭球坐标和，将这2 个坐标集转换为局部地平系统，即

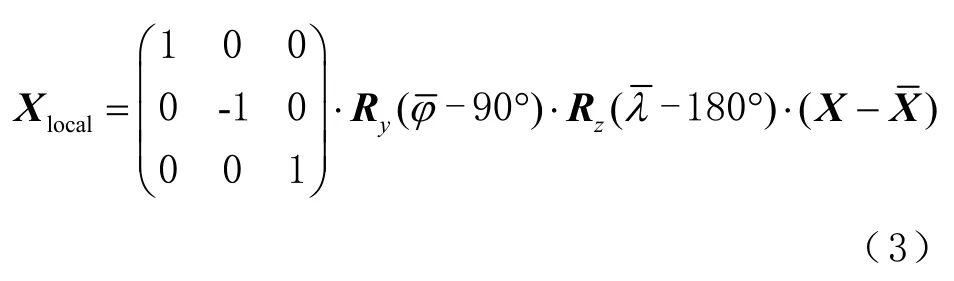
式中：Xlocal为局部地平坐标系坐标矩阵；Ry和Rz为y轴或z轴的选择矩阵；和为重心X的椭球坐标；X为须转换的坐标向量。

按式（4）变换输入坐标集与参考坐标集之间差的平方和，通过最小二乘法来估计方程中的Helmert 变换参数。

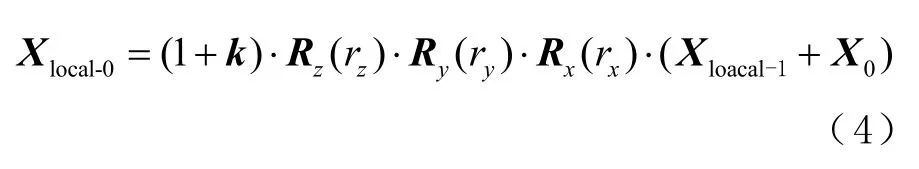
式中：Xlocal-0为小区域的参考坐标集局部地平系坐标；Xlocal-1为小区域输入坐标集局部地平系坐标。

无论大区域还是地方小区域，在确定了3 个平移参数、3 个旋转参数、1 个比例因子之后，可以根据式（5）将输入坐标转换系至参考坐标系，得到转换后的参考坐标系坐标，即

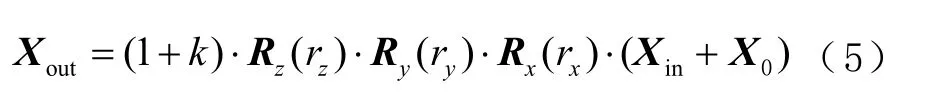
式中：Xout为转换后参考坐标矩阵；Xin为输入坐标矩阵。

然后与原参考坐标系坐标进行比较，得到转换后的残差，为：

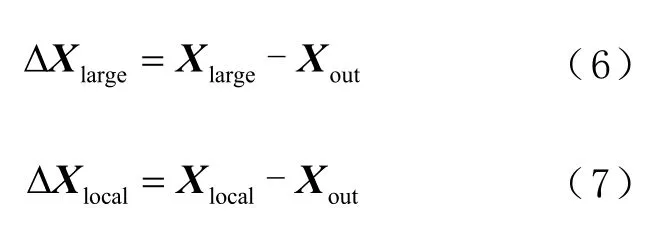
式中：ΔXlarge为大区域转换后残差矩阵；ΔXlacal为小区域转换后残差矩阵。

计算转换得到的参考系坐标集与对应的原参考坐标集的差异值，即N（北）、E（东）、U（天顶）3 个方向的模型残差分量[6]，获得Helmert 转换残差，当N、E、U 3 个方向的坐标模型残差大于该方向上综合中误差的3 倍的时候，即可判断该坐标不符合2 个坐标集的整体一致性。

在高速铁路框架控制网平差基准一致性检验中，可采用以上方法准确判断和定位有问题的高等级已知点。

2 实验与结果分析

本文采用2017 年年积日第214—222 天，某铁路CP0的数据进行实验分析。该数据分2 轮进行外业观测，每轮同步观测5 个时段，白天和夜间观测均匀分布，时间不低于5.5 h，轮间搭接2 个CP0 控制点，每个时段数据合格。求解14 个CP0控制点，基线解算和平差计算的起算点选用周边10 个 IGS 站，即北京房山站（BJFS）、长春站（CHAN）、拉萨站（LHAZ）、波利根站（POL2）、上海天文台站（SHAO）、韩国站（SUWN）、中国台湾桃园站（TWTF）、蒙古站（ULAB）、乌鲁木齐站（URUM）、武汉站（WUHN），在2017 年年积日第214—222 天期间内，这些IGS 站的数据均比较完整，数据质量良好，P1 多路径影响mp1和P2 多路径影响mp2 值均小于0.5 m。CP0 及IGS基准站网型如图1 所示。

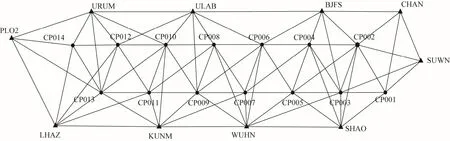
图1 CP0 及IGS基准站分布网型

2.1 数据处理

高精度基线解算采用麻省理工学院（Massachusetts Institute of Technology,MIT）和美国斯克里普斯海洋研究所（Scripps Institution of Oceanography,SIO）联合开发的加米特（GAMIT）/格洛布克（GLOBK）软件10.70 版本[7]。GAMIT/GLOBK 软件主要功能模块包括轨道积分程序、观测方程构建程序、单差自动修复周跳程序、双差自动修复周跳程序、交互式修复周跳程序、最小二乘求解程序等[8]。软件基于多种改正模型，采用优化的策略，可针对上千千米的超长基线，实现毫米级的高精度基线解算[9]。

在基线解算中，固定站的N、E、U 3 个方向分别进行松弛约束，约束分别为5、5、10 cm，分别得到年积日第214—222 天共9 个时段的10 个IGS 站的单时段松弛解，这10 个IGS 站为BJFS、CHAN、LHAZ、POL2、SHAO、SUWN、TWTF、ULAB、URUM、WUHN。

2.2 Helmert 转换坐标残差指标定位异常点

在得到单天松弛约束解后，分别提取BJFS、CHAN、LHAZ、POL2、SHAO、SUWN、TWTF、ULAB、URUM、WUHN 等10 个站的每个时段的松弛约束解的空间直角坐标，作为第1 个坐标集；收集该10 个站在国际ITRF2014 框架内标准历元坐标作为参考数据集；对第1 坐标集和参考坐标集进行Helmert 转换；根据Helmert 转换参数计算坐标转换残差。根据Helmert的坐标残差指标可以定位异常点。

本次采用Helmert 模型计算10 个IGS 站单个时段松弛解坐标与 ITRF2014 标准历元坐标的Helmert 转换坐标残差。残差如表1 所示。

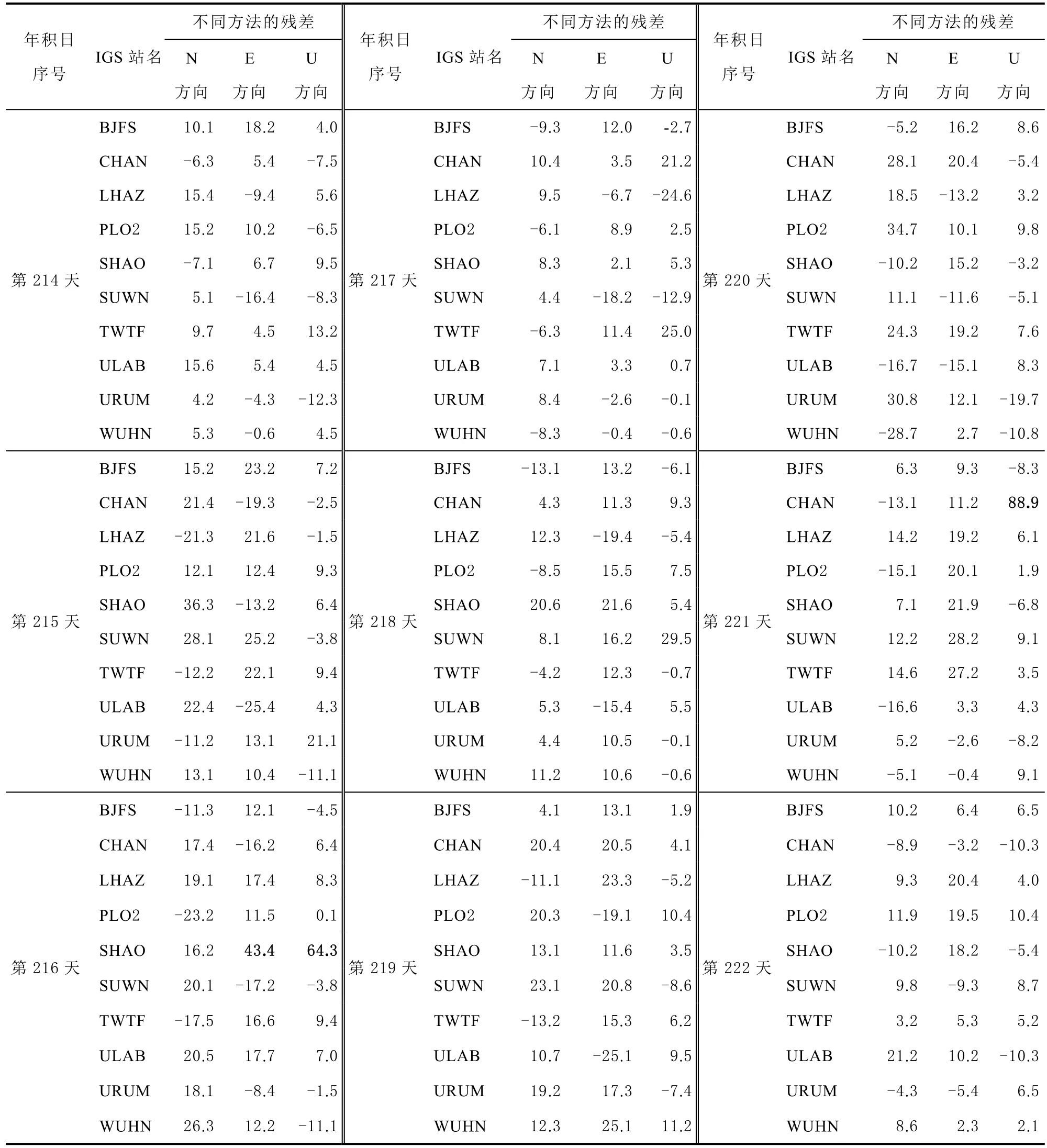
表1 各时段松弛解Helmert 转换坐标残差 mm

由表可知：2017 年年积日第216 天SHAO 站在E 方向的残差为43.4 mm，大于2 倍中误差，U方向残差为64.3 mm，大于3 倍中误差；2017 年年积日第221 天，CHAN 站在U 方向的残差为88.9 mm，大于3 倍中误差。

由此可以判断出2017 年年积日第216 天的SHAO 站、2017 年年积日第221 天的CHAN 站存在数据质量问题，导致了解算的坐标精度降低，需要将其剔除掉重新计算，才能保证基准平差不引入基准误差。

2.3 单天解卡方检验

卡方检验是一种非连续性资料的假设检验方法。基于卡方检验可实现3 种检验：①拟合度检验，比较2 个及2 个以上样本率；②相关性分析，2 个分类变量之间有无关联性；③统一性检验，检验2 个或2 个以上总体的某一特性分布[10]。

在GLOBK 平差中，可以通过卡方检验来宏观了解平差基准误差的大小。平差后的卡方检验值越小越好，如果卡方检验值大于1，说明平差基准存在误差。本实验将通过卡方检验方法来验证前期Helmert的分析结果。

实验对9 个时段分别进行了单天平差计算，约束10 个IGS 站，采用GAMIT/GLOBK 软件对每天的基线文件进行平差计算，在获取单天解的同时也可以得到单天解的卡方检验值。该数据平差后的单天解卡方检验值如表2 所示。

表2 单时段平差的卡方检验

由表可以看出：2017 年年积日第216 天和第221 天这2 个时段的卡方检验大于1，说明这2 个时段约束平差的固定基准存在不一致的情况，但不能定位是哪些站出了问题。根据前面Helmert 残差分析的情况，可以更加准确地定位到出现问题的约束站，说明利用Helmert 残差可以确定异常基准点。

后面的平差过程需要针对有问题的时段，将有问题的站松弛开，约束其他没有问题的基准站重新进行单天约束平差。如果卡方检验通过，则须在单天数据中剔除掉有问题的基准站，或者替换成其他基准站，重新计算基线和平差。

3 结束语

本文通过与约束平差的卡方检验指标进行对比，证明利用Helmert 模型计算残差来发现和定位有问题的基准站是可行的。在CP0 数据处理中，尤其是对大区域或者含IGS 站在内的超大区域的CP0 数据进行处理时，必须严格验证所选国家A级、B 级GNSS 控制网或IGS 站等高等级已知点的坐标一致性。通过Helmert 模型能够分析出高等级已知点异常坐标，准确定位异常数据，从而避免将误差带入控制网中，最终提高控制网的计算精度。