毒气泄漏事故中人员撤离路径规划
2021-08-29高宏兵
范 强,高 鹏,高宏兵
(1.辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000;2.大连九成测绘信息有限公司,辽宁 庄河 116400)
0 引言
随着我国化工产业的迅猛发展,化学品的产量以及销量呈现直线上升的趋势,导致毒气泄漏事故频繁发生。由于毒气泄漏事故具有范围性、复杂性及灾难性等特征,一旦发生泄漏会对人的生命造成重大威胁;因此为减少毒气泄漏带来的危害,须及时有效地对人员进行疏散,而如何合理有效地规划撤离路径是亟待解决的重要问题。
在毒气泄漏的环境中,撤离路径的规划不仅需要考虑撤离的距离与时间,还需要考虑人员在疏散过程中所受到的毒气伤害大小以及相应的伤亡概率。因此本文通过对疏散路径的规划提出相应的约束条件,并采用毒性负荷累积值[1]来定量评估人员在疏散过程中所受毒气伤害的大小,利用普罗比特(Probit)模型对疏散人员的伤亡概率进行估计,实现对撤离路径的合理规划;并且在此基础上,依据规划好的撤离路径,利用交通分配模型对撤离人员进行分配,旨在最短时间内将尽可能多的人员疏散至安全位置,从而减少毒气泄漏事故带来的损失。
1 风险区域划分
毒气负载指数是定量描述生物体暴露在毒气环境中自身所受到的伤害,它与生物体所处区域毒气的浓度以及在该浓度下暴露的时间有关。毒气负载指数的一般表达式[2]为

式中:T指毒气负载值,是对生物体所受伤害大小的量化指数;C为生物体所处区域的毒气浓度,单位为mg/m3;t为生物体在该浓度下所暴露的持续时间,单位为min;m与n分别为毒气浓度与持续暴露时间的作用指数。当m值大时,说明长时间处于低浓度环境比短时间处于高浓度环境的危害小,反之则说明,长时间处于低浓度环境比短时间处于高浓度环境的危害大。
作用指数m、n的取值根据毒气成分的不同而不同,到目前为止,该指数的获取方式是生物体的暴露实验。1996 年,美国环保局采用以往的生物体实验数据为基础数据,联合开发了急性暴露指南标准[3(]acute exposure guideline levels,AEGL),该标准用以定量衡量人体在短时期内暴露于高浓度毒气范围中所受到的伤害。该标准设置了3 个测定点:AEGL-1、AEGL-2 以及AEGL-3,分别表示身体不适、生物体受到无法康复的伤害以及威胁生物体生命安全。该标准通过以往的实验数据,选择与毒气类型相匹配的m、n值,计算出每个测定点在不同时期(10 min、30 min、1 h、4 h 以及8 h)的浓度阈值[4-6]。
毒气负载指数与AEGL 标准结合,通过计算可对风险区域进行不同程度的划分。计算过程如下:
1)计算生物体暴露时间t,t=M/Q,其中M为毒气泄漏总量,Q为毒气泄漏源强。
2)根据式(1)计算3 个测定点的毒气负载指数TAEGL-i以及毒气覆盖区域范围内任意一点的毒气负载值T。
3)通过对T与TAEGL-i进行比较,划分为4 个不同等级的危害区域:①当T≤TAEGL-1时,为轻度反应区;②当TAEGL-1
2 撤离模型改进
通常情况下,疏散路线一般选用距离最短、所用时间最少的路径,即最短路径;但在有毒气体发生泄漏的环境中,撤离路线的选择不仅要考虑避开对人体造成严重伤害的致死区及致伤区,还须考虑在撤离途中毒气在人体内的累积值。由于性别、年龄以及健康状况的不同,导致每个人所能承受的毒气累积值也不同。因此为使撤离路线更加符合实际要求,须选出毒气累积值相对最小的撤离路径,并且还要保证在撤离过程中人员的伤亡率最小。
2.1 路径遍历优化
由于最短路径在实际撤离路线中不一定为最优撤离路线,因此想要计算出最优撤离路线首先须计算出所有可能的路线。如果发生毒气泄漏区域的道路网络较为复杂,就会使得求解所有路径较为繁冗,所需时间较长,求解结果也可能达不到预想的精度;因此本文提出一种约束型求解所有路径的方法,其核心思想是增加约束条件,从而达到减少道路网络节点的目的,能够快速准确地求解出所有路线。其原理流程如图1 所示。
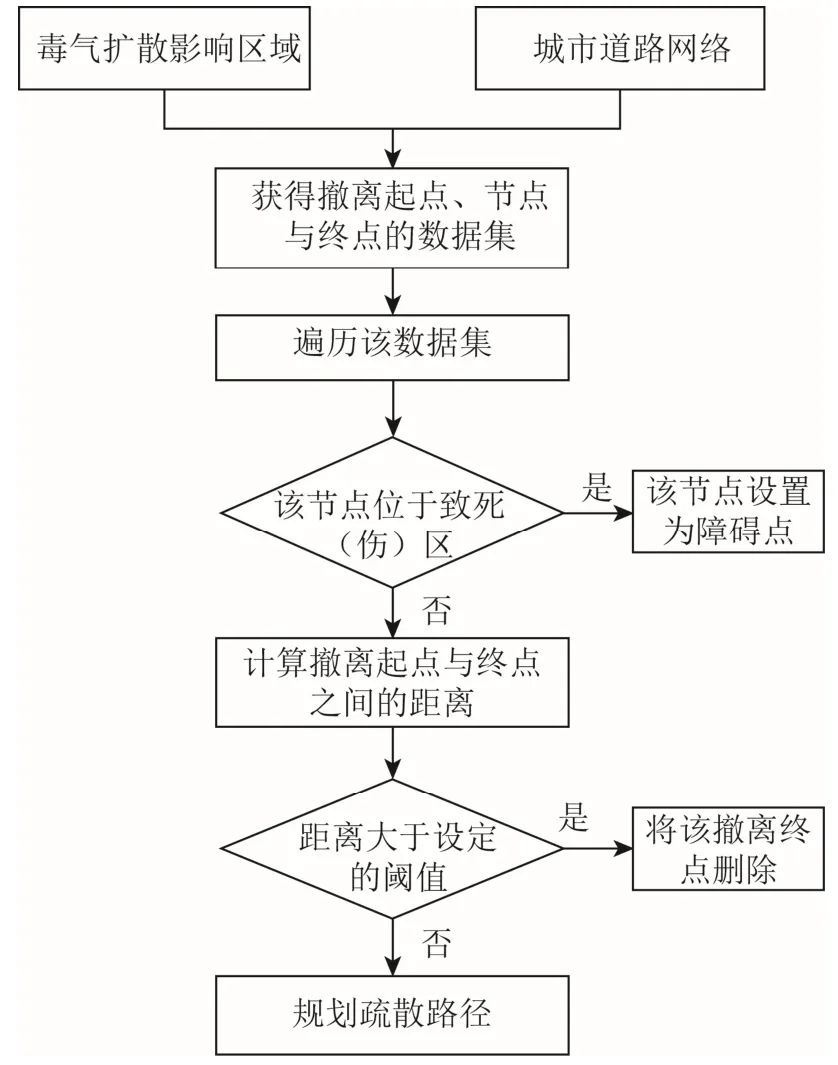
图1 路径遍历优化算法原理流程
首先,构建撤离道路网络[7-8],通过将当前毒气泄漏区域内的道路网络与毒气扩散的影响范围进行叠加分析,形成撤离起点、撤离节点以及撤离终点3 个数据集,并以这3 个数据集为基础构建撤离道路网络。这3 个数据集分别为:①撤离起点,毒气影响范围内的道路网络节点,是撤离的起始节点;②撤离节点,符合约束条件的有毒气体影响区域内的道路网络节点,是撤离的中间转点;③撤离终点,道路网络节点与毒气影响区域边界的交点,是人员撤离毒气影响范围的出口,即撤离终点。
其次,利用约束条件对撤离道路网络内的节点进行遍历筛选,提高路径的遍历速度与准确度,相应的约束条件为:①为避免撤离人员受到额外伤害,将致死区及致伤区边界与道路网络节点的交点从撤离节点中去除,即设置为撤离障碍点;②减少撤离终点的数量,即将毒气影响范围与道路网络叠加剪切,选择其边界交点作为撤离终点,避免出现撤离终点冗余的情况;③去远原则,即通过计算撤离起点与撤离终点的距离,去掉最远终点,因为这些撤离终点明显不符合撤离的要求。
最后,依据遍历结果对撤离路径进行规划。
2.2 人员危害评估
2.2.1 毒气负载累积值的确定
在人员撤离过程中,随着人员的移动,在不同时间不同地点所遭受的毒气浓度值是不同的,因此需要通过计算毒气负载累积值来动态量化撤离人员所受到的伤害。毒气负载累积值的计算需要将撤离路径分割为等距离的间隔,在每个间隔设置1 个浓度点,并假设每个间隔的浓度值与上1 个浓度点的浓度值相等,从而将撤离路径分割为一系列浓度值不同的路段。其中,为使每个浓度采样点的浓度至更加精确,将每个间隔设置为1 m,与高斯扩散模型的单位增量一致,则撤离路线上毒气负载累积值TP的公式为
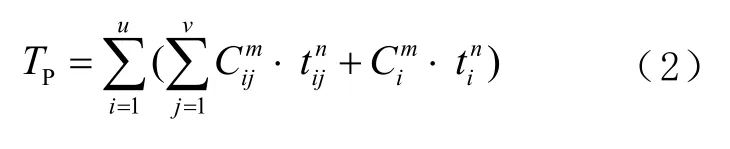
式中:u为撤离路线所包含的路段数;v为该路段所包含的浓度点个数;Cij为第i条路段的第j个浓度点的毒气浓度值;tij为第i条路段上由第j个浓度点到达第(j+1)个浓度点所需的时间;Ci为连接第i与第(i+1)条路段道路节点的毒气浓度值;ti为通过节点i的所需时间。
2.2.2 人员危害评估
通过选择相对最小的毒气负载累积值所在的路径作为撤离路径,虽然可以在很大程度上降低毒气对撤离人员的伤害,但在疏散过程中人员还是会面临着生命的威胁,而Logit[9]模型与Probit[10-11]模型是目前用于估计在有毒物质与热辐射影响下人员死亡概率的2 种最常用模型。由于人员在撤离过程中,在不同时间不同位置所受到的毒气伤害不同,因此本文通过将Probit 模型与毒气负载累积值相结合,来对死亡概率值Pr进行估算,具体计算方法如式(3)所示,其中死亡概率值需转换为与之相对应的死亡概率,其转换公式可参考文献[12]。
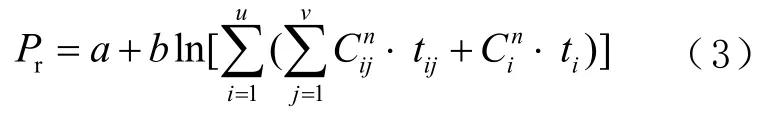
式中:Pr为在暴露在毒气环境下的死亡概率值;a、b、n为不同毒气性质所对应的毒性常数;C为该毒气的浓度,单位为mg/m3;t为暴露在该毒气环境中的时间,单位为min,最大值为30 min。
3 优化交通分配模型
在撤离路线确定后,每条撤离路线上的人员分配就成为了下一个需要解决的问题;而人员分配需要保证在有限时间以及有限容量的条件下,尽可能多地疏散人群。该问题的实质是一种起讫点(origin-destination,OD)问题[13],就是预测2 点间的出行总量,按照某种符合实际要求的规则,将其合理地分配到各路段上。交通分配模型按照沃德罗普(Wardrop)准则分为平衡模型与非平衡模型,符合Wardrop 第一、第二准则的平衡模型分别为用户最优(user equilibrium,UE)平衡模型以及系统最优(system optimal,SO)平衡模型,不使用Wardrop 原理的模型称为非均衡模型[14]。
非均衡模型按照分配方法分为最短路径(全有全无)分配、多路径分配、容量限制单路径分配及容量限制多路径分配4 类。由于道路容量有限,且随着人数的增加,道路阻抗也随之变化,故此类问题称为阻抗可变分配问题。该问题的解决方法有增量分配法与迭代加权法2 种。增量分配法可以通过人为设定比重进行迭代,但如果初次迭代时在某一路段分配过多流量,而次路段的通行能力较低,就会导致该算法无法得到正确解。迭代加权法是将附加量与原流量进行加权平均,作为该路段新的交通量,并重新计算交通阻抗进行迭代,直至前后2 次分配结果近似相等时,迭代停止。但本文用于人员疏散分配,须使得疏散时间最短(即道路总阻抗最小),故对迭代加权算法的收敛条件进
行改进,从而使其更加符合实际撤离情况。改进的迭代加权法算法步骤:
1)初始化。按照各路段的无阻抗行走时间进行全有全无分配,得到各路段的交通量=0,∀路段a,令迭代次数k=0;
3)按照新的行走时间以及OD 交通量进行全有全无分配,从而得到各路段的附加交通量
车辆在道路上的行走时间是随着交通流量的增加而增加的,其行走时间一般用美国联邦公路局(Bureau of Public Road,BPR)函数[15],其表达式为
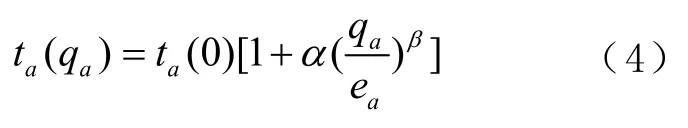
式中:ea为路段a的交通容量,即单位时间内可通行的最大车辆数;ta(0)为道路a上的平均车辆自由走行时间;qa为当时通过该路段的交通量;α、β为待标定系数,BPR 建议α、β的取值为0.15、4。
4 实验与结果分析
图2 所示为某地区的道路网络与毒气影响范围叠加裁剪后生成的撤离道路网络图。为了便于实验研究,将其抽象为图论的形式。按照本文提出的约束条件对撤离路线进行改进,其中撤离起点为A,撤离终点为B、C、D、E,其关系网络图及彼此之间的距离如图3 所示。
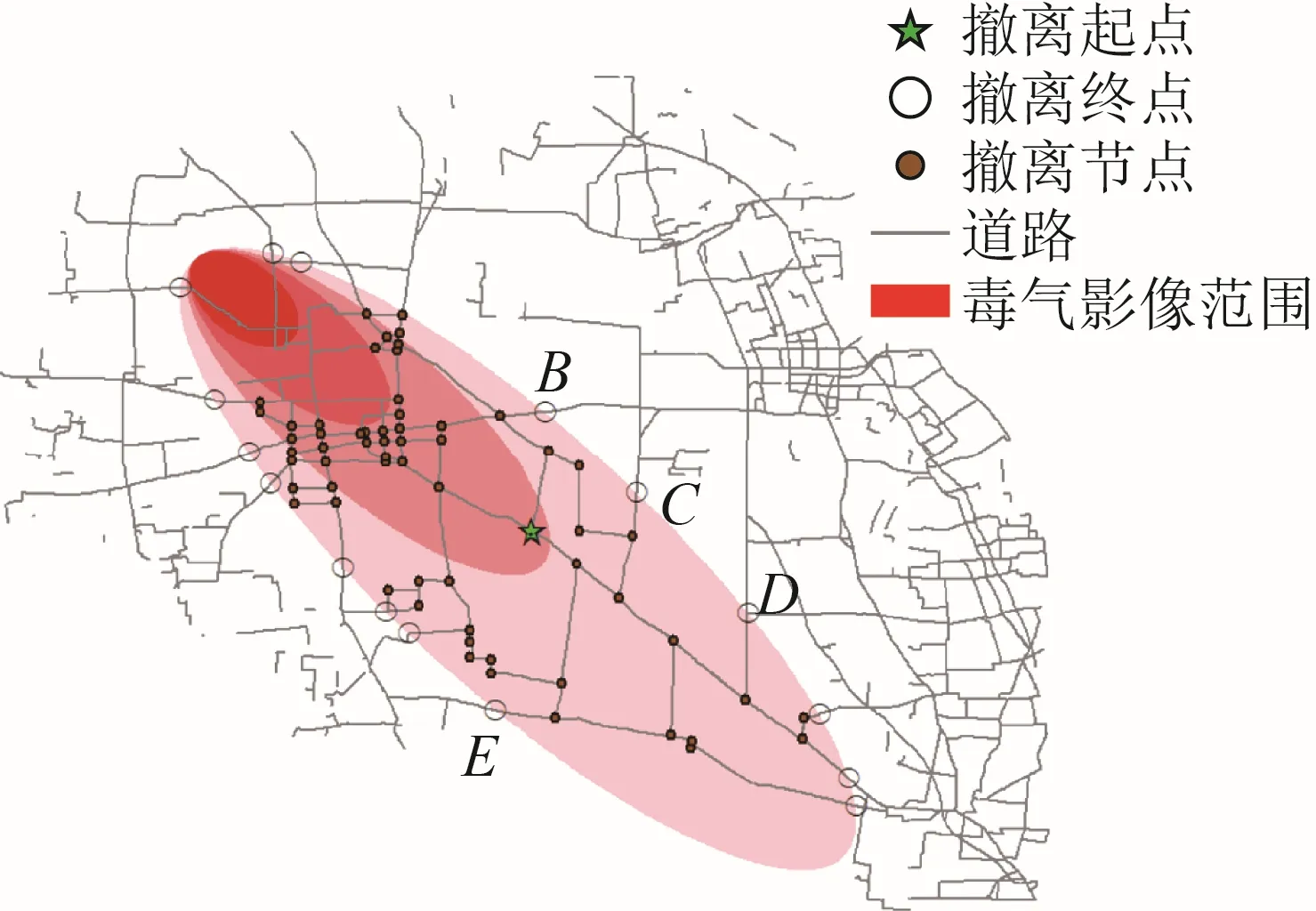
图2 撤离道路网络
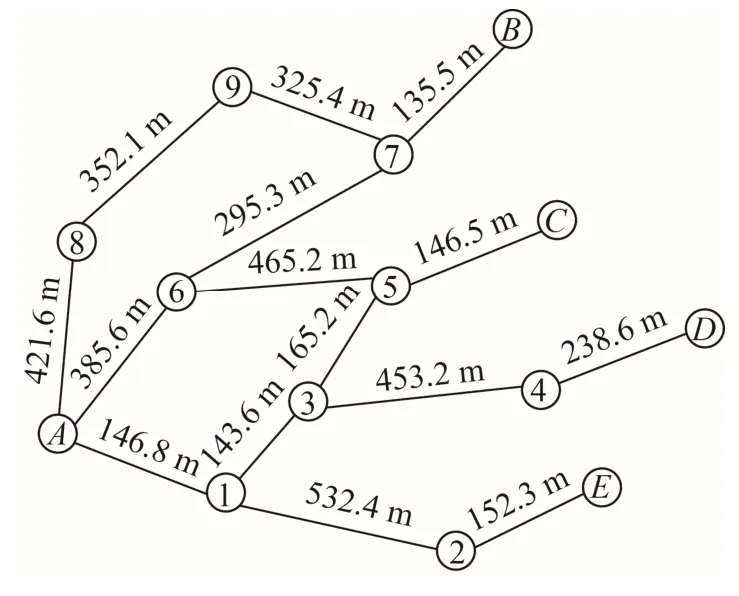
图3 节点位置信息
根据本文对撤离路线选择的约束条件计算出撤离起点到达撤离终点所有可能的路径,并采用深度优先遍历方法[16]对各节点进行标记、添加、删除以及输出,计算出所有路线。其算法主要步骤如下:
第1 步)输入撤离起点与撤离终点数据集,建立节点网络信息邻接表,生成临时路径信息数据集;
第2 步)选择撤离起点A,对其进行标记,通过深度优先遍历法以及节点网络信息数据表寻找符合条件的下一个节点,将其添加到临时路径信息数据集中,并对其进行标记;
第3 步)如果到达撤离终点,输出当前路径信息,并将撤离中从临时路径信息数据集中删除,同时返回上一个节点,再次按照深度优先进行遍历,寻找正确的节点,对其进行标记,并添加到临时路径中;
第4 步)重复执行第3 步以及第2 步,直至遍历过所有节点,并全部标记,输出所有正确路径,删除临时路径信息数据集以及节点网络信息邻接表。
本次实验以氨气泄漏为例,采用高斯烟羽模型[17]计算各节点的浓度值信息,按照路线信息计算每条路径上的毒气负载累积值,其中假设人员的撤离速度为1.2 m/s,结果如表1 所示。
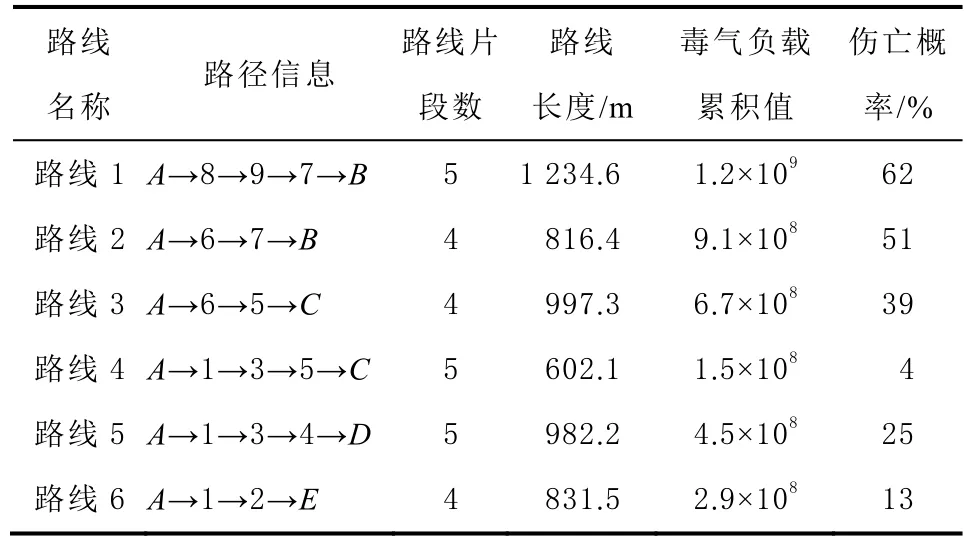
表1 撤离路线信息表
根据撤离路线信息表可知,路线4、路线5 及路线6的毒气负载累积值以及人员的伤亡概率较低,可作为撤离路线。虽然路线2的距离较短,但其相对应的毒气负载累积值与人员伤亡概率较大,因此不可作为撤离路径。假设撤离起点共有10 000人,根据每条道路长度、宽度、容量及阻抗大小不同,按照改进的迭代加权法对其每条撤离路线进行人员分配,分配结果如表2 所示。

表2 撤离人员分配信息表
由表可知,利用改进的迭代加权法得出的人员分配方案与各撤离路径上的人员伤亡率相对应,即人员伤亡率越低的路线上人数的分配结果越多。如线路4的人员伤亡概率仅为4%,但在该路线上的人员分配数量达到了5 000 人,说明该方法在各撤离路径上的人员分配方案可为实际撤离中的人员分配提供有益参考。
通过对以上实验结果分析发现:本文对撤离路径选择所提出的方法,不仅大大降低了路径的遍历速度并提高了遍历的准确性,而且更加符合实际中对撤离路线的要求;除此之外,根据改进的迭代加权法所得出的在各撤离路径上的人员分配方案,对于现场撤离人员的分配亦具有一定的指导意义。
5 结束语
本文针对在毒气泄漏环境中人员撤离路径的选择问题,提出了有约束的撤离路径,并以毒气负载累积值以及人员死亡概率为基础,构建了撤离路线模型。模型中不仅考虑到人员在撤离过程中在不同地点不同时间所受到的伤害不同,从而计算毒气负载累积值,用以量化人员在撤离途中所受到的伤害;而且通过Probit 模型对人员的死亡概率进行评估,同时对非均衡分配法进行优化,从而得到各撤离路线上的人员分配方案,使得撤离人员能够在相对用时最少且所受伤害最小的情况下完成撤离,对于指挥人员的决策及现场人员疏散有着较重要的参考价值。
