基于反步控制的多AUV编队控制方法研究∗

蔡文郁，杨俊雷，官靖凯

(杭州电子科技大学电子信息学院，浙江 杭州 310018)

自主水下航行器(Autonomous Underwater Vehicle，AUV)具有自治性强、机动性高等特点，在海洋观测、海上救援、管道检测等领域具有广泛的应用前景。面对更加复杂的水下任务，多AUV集群系统凭借着良好的冗余性、协调性和高效性，为海洋探索任务提供了新的解决思路。AUV编队技术作为多AUV集群系统的关键技术之一，编队方案如图1所示，目前已经受到了各国研究者们的广泛关注。海洋环境中存在诸多不确定因素，包括海流、海浪、水下通信约束等外部因素的影响，对编队控制而言是一个很大的挑战，AUV集群编队控制系统的设计有着严格的要求，必须兼具良好的稳定性和鲁棒性。

图1 集群编队方案

目前国内外常用的编队控制方法大致可以分为虚拟结构方法[2－5](Virtual Structure Method)、基于行为的方法[6－8](Behavior-Based Method)、人工势场方法[9－11](Artificial Potential Field Method)和领导跟随者方法[12－18](Leader-Follower Method)。由于领导跟随者方法具有良好的网络拓扑结构特性，近年来很多研究者都针对领导跟随者方法进行了改进:Yan等人[12]基于图论和虚拟领导者设计了新的编队结构，这种特殊结构将AUV之间的连接固定为通过引线和邻域AUV形成的三角形，因此增加了结构的刚度和位置精度，增加了编队结构的稳定性。李娟等人[13]提出了一种结合水下机器人路径规划和编队控制的控制器，在控制器中采用滑模控制方法实现AUV路径跟踪控制，将位置、姿态和速度跟踪转换为虚拟速度控制，使AUV达到预期位置。Panagou和Kumar[14]提出了一种在已知障碍物环境中，在通信约束情况下的机器人协同运动方法，不需要机器人之间的数据交互，而是基于本地信息分散地执行各自任务。Stover等人[15]提出了一种策略，在队形保持的过程中跟随者的位置不是相对于领导者位置严格固定的，而是以领导者参考系为中心的等距离圆弧上适当的变化。Ji等人[16]提出了一种基于停滞规则的领导者跟随者混合控制方案，一旦领导者到达理想的阵型，跟随者会汇聚到领导者为中心的凸多面体中，当所需的领导者任务失败时，领导者会形成一个固定队形，且拥有相同的速度和方向，因此跟随者以与领导者相同的速度和方向收敛。由于多AUV系统与神经网络具有相似的特性，一些研究人员也试着将神经网络与编队控制相结合，取得了良好的效果。例如Li和Zhu[17]提出了一种自适应自组织图(Self-Organizing Maps，SOM)神经网络方法，用于水下机器人集群的分布式编队控制，包括对网络初始神经权重的特殊定义、获胜者的选择规则、工作量平衡定律、权重的更新方法以及编队跟踪策略。每台AUV控制器仅仅使用自身信息和相邻AUV的有限信息，而没有明确指定领导者和跟随者，所有AUV均被视为领导者或追随者，因此它们具有更好的适应性和容错能力。针对需要躲避障碍物的复杂编队控制场景，Ding和Zhu等人[18]采用生物启发神经网络模型实现了AUV的三维编队控制与避障。神经网络中的每个神经元代表先导AUV的一个步骤，领导者AUV通信线路由神经网络中神经元的输出活动值确定，最终领导者AUV的导航转化为神经网络中神经元输出的活动值。

本文以领导者跟随者的编队方法为基础，根据实际领导者跟随者编队模型，借鉴反步控制法的思想提出了一种基于几何数学模型的新型控制策略。而且，利用李雅普诺夫理论证明了在该控制策略下，AUV集群系统能够达到稳定状态，最后在MATLAB平台上进行了仿真验证。

1 编队模型

本文采用了基于领导者跟随者的编队模型，通过领导者AUV的位置、姿态、速度等信息，建立虚拟领导者，跟随者AUV动态地调节自身的状态，完成路径的跟随。假设多AUV系统模型由N台AUV组成，为了简单起见，假设它们处在恒定深度的平面运动，第i个AUV的状态可以用下式描述:

式中:ηi＝[x i，y i，ψi]T表示在全局坐标系下第i个AUV的位置和姿态信息，v i＝[u i，v i，r i]T表示第i个AUV在自身所在载体坐标系下的速度矢量。根据坐标系转换矩阵可知从全局坐标系到AUV载体坐标系的转换矩阵为:

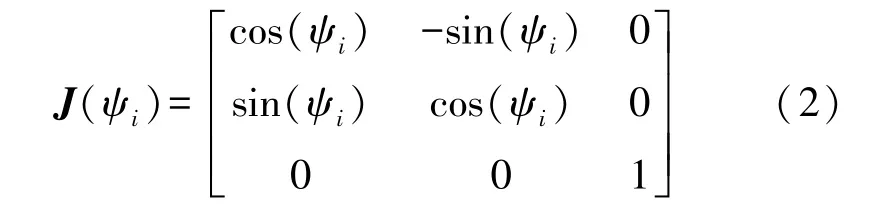
在Leader-Follower集群模型中，跟随者通过领导者的位置、姿态动态的调整自身的位置姿态。由于跟随者的轨迹是随着领导者运动而生成的，本文引入了虚拟领导者的概念，虚拟领导者是以领导者AUV为参考点，按照几何关系生成其位置，因此虚拟领导者本质上可以认为是跟随者AUV的理想位置。在笛卡尔坐标系中的多AUV系统运动模型如图2所示。

图2 多AUV编队模型

图2中深色的AUV是AUV实际所在位置，浅色的AUV是编队模型中虚拟领导者的位置。假设编队模型设置为图中所示的正三角形，控制律的目标就是让跟随者AUV运动到理想位置，并能保持住队形和姿态跟随领导者AUV继续运动。本文用ηL＝[x L，y L，ψL]T和ηF＝[x F，y F，ψF]T分别表示领导者AUV和跟随者AUV的坐标以及速度矢量。从图2可以看出，通过领导者的状态可以计算出跟随者AUV的理想坐标:

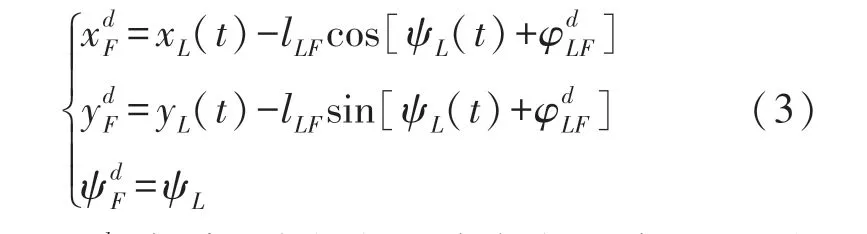
式中:l LF和分别是虚拟领导者与领导者AUV之间的距离与角度。考虑虚拟领导者位置以及AUV的真实所在位置，全局误差ErrF＝表示AUV的实际位置与理想位置的误差，其中表示AUV理想位置与AUV实际位置在全局坐标系下X轴的误差，表示的是AUV理想位置与AUV实际位置在全局坐标系下Y轴的误差表示AUV理想位置与实际AUV的航向角误差。

全局坐标系下的AUV误差模型为:

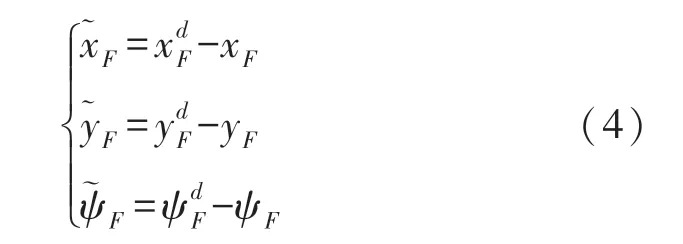
假设在整个AUV系统运动过程中，领导者AUV遵循以下约束:

式中:umax和rmax分别是领导者AUV的最大线速度和角速度。

接下来分析跟随者AUV和它所对应的虚拟领导者之间关系，根据上述公式以及坐标系转换矩阵将坐标原点固定在虚拟领导者AUV，并建立载体坐标系，从而可得AUV载体坐标系误差模型:

式中:x e表示虚拟领导者AUV与AUV实际位置在载体坐标系下的X轴误差，y e表示载体坐标系Y轴上的误差，ψe表示虚拟领导者与AUV实际位置的航向角误差，ψe∈(－2π，2π)。

定义转换成矩阵为:

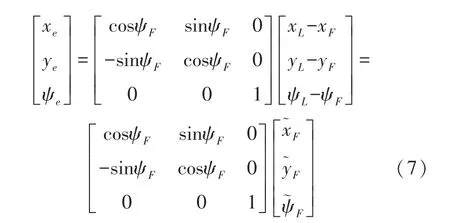
通过执行上述变换，跟随者的位置将从全局坐标转换为载体坐标。在载体坐标系中，对误差求微分可得领导者和跟随者之间动态误差的微分模型:

因此，本文的目标是设计合适的控制律减小AUV实际位置与虚拟领导者之间的误差，如下式所示:

2 控制策略

本文研究的运动学控制器模型如图3所示，将虚拟领导者的状态与自身的位置和姿态信息输入到运动学控制器模型可计算出当前时刻的理想速度与角速度，同时更新自身位姿，最终形成优化的闭环控制。

图3 控制器模型

为了实现AUV编队的全局轨迹跟踪控制，定义了如下数学变换:

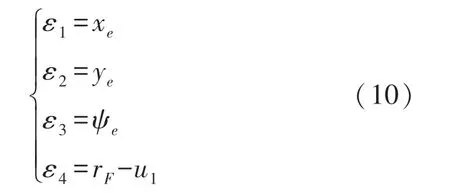
式中:u1为引入的虚拟变量，将式(10)代入微分误差方程式(8)，可得:

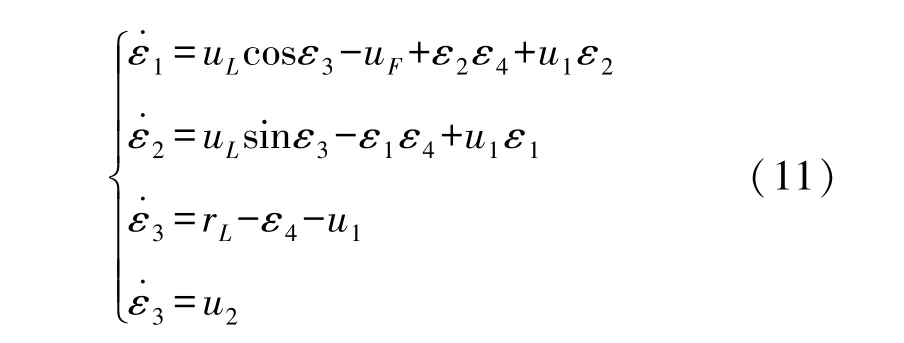
式中:矩阵ε表示为:ε＝[ε1，ε2，ε3]T。f i和g i为函数的集合，如式(13)和式(14):

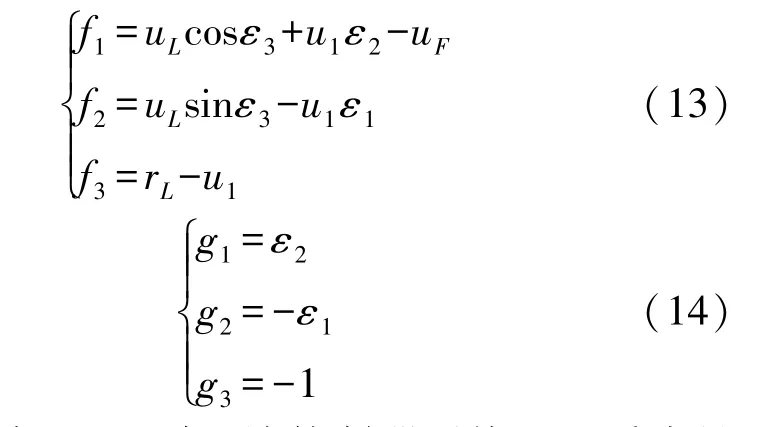
根据上式(11)可知，该控制器系统可以看成是一个通过积分环节串联的非线性系统，因此可利用反步控制法思想。根据李雅普诺夫定理可知，如果可以证明和有界且u L>0，则存在控制律使得上式所描述的误差系统渐进稳定。本文先选取式(11)中的第1个子系统如下:

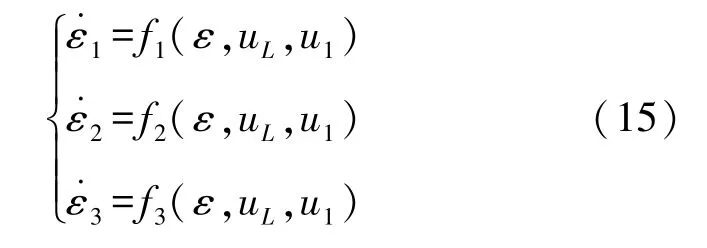
为该子系统设计一个李雅普诺夫函数，如式(16)所示:

可以选取如下的控制律:

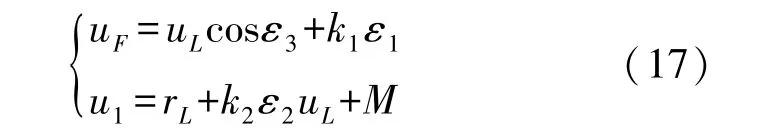
式中:M＝sinε3/k3，k1、k2、k3都是大于0的常数，则可得到如下公式:

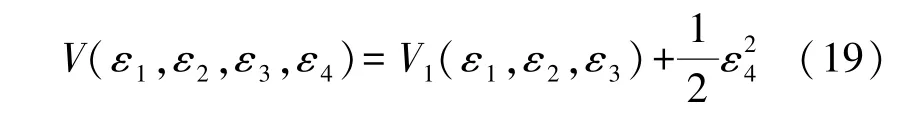
选择如下的控制律:

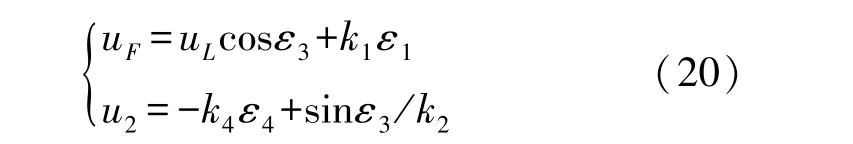
代入式(19)可得到:

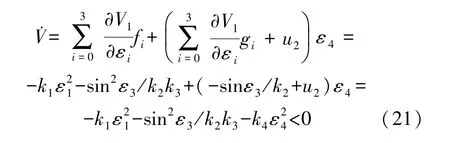
负定，因此在如式(20)所示控制律的作用下，如式(11)所示的系统能够获得渐进稳定，由式(10)可知，如式(8)所示的系统与如式(11)所示的系统能够一样获得渐进稳定。

综上所述，本文提出的AUV集群编队系统的控制律定义如下:

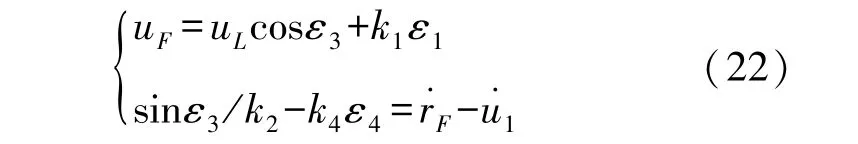
也可以表示为:

式中:u1为虚拟控制输入，如式(24)所示，k1，k2，k3，k4都为常数。

3 仿真结果

为了验证本文控制方法的可行性，利用MATLAB R2016a软件平台对一个领导者AUV、两个跟随者AUV的情况进行编队仿真。三台AUV在坐标系原点周围随机部署，假设有海流等环境因素的干扰，选取[－0.15，0.15]的白噪声强度。仿真主要参数如表1所示，主要是本文控制律中的四个参量取值。

表1 仿真参数

多AUV的编队仿真结果如图4所示，图4(a)是理想的编队轨迹，图4(b)是在本文提出控制策略的编队轨迹。图中实线轨迹是领导者AUV的轨迹，虚线轨迹是两台跟随者AUV的轨迹。

由图4所示的AUV仿真轨迹图可以看出，在本文设计的控制器作用下，AUV编队轨迹与理想状态接近，编队效果良好。两台跟随者AUV的速度、角速度如图5所示，其中点线与点划线曲线为需要达到的理想线速度曲线和理想角速度曲线，虚线与实线曲线依次为线速度变化曲线与角速度变化曲线。跟随者误差定义为跟随者的实际位置与期望位置差值的绝对值。两台跟随者AUV的误差变化曲线图如图6所示，实线，虚线，点划线曲线依次表示X轴、Y轴和航向角的误差曲线。

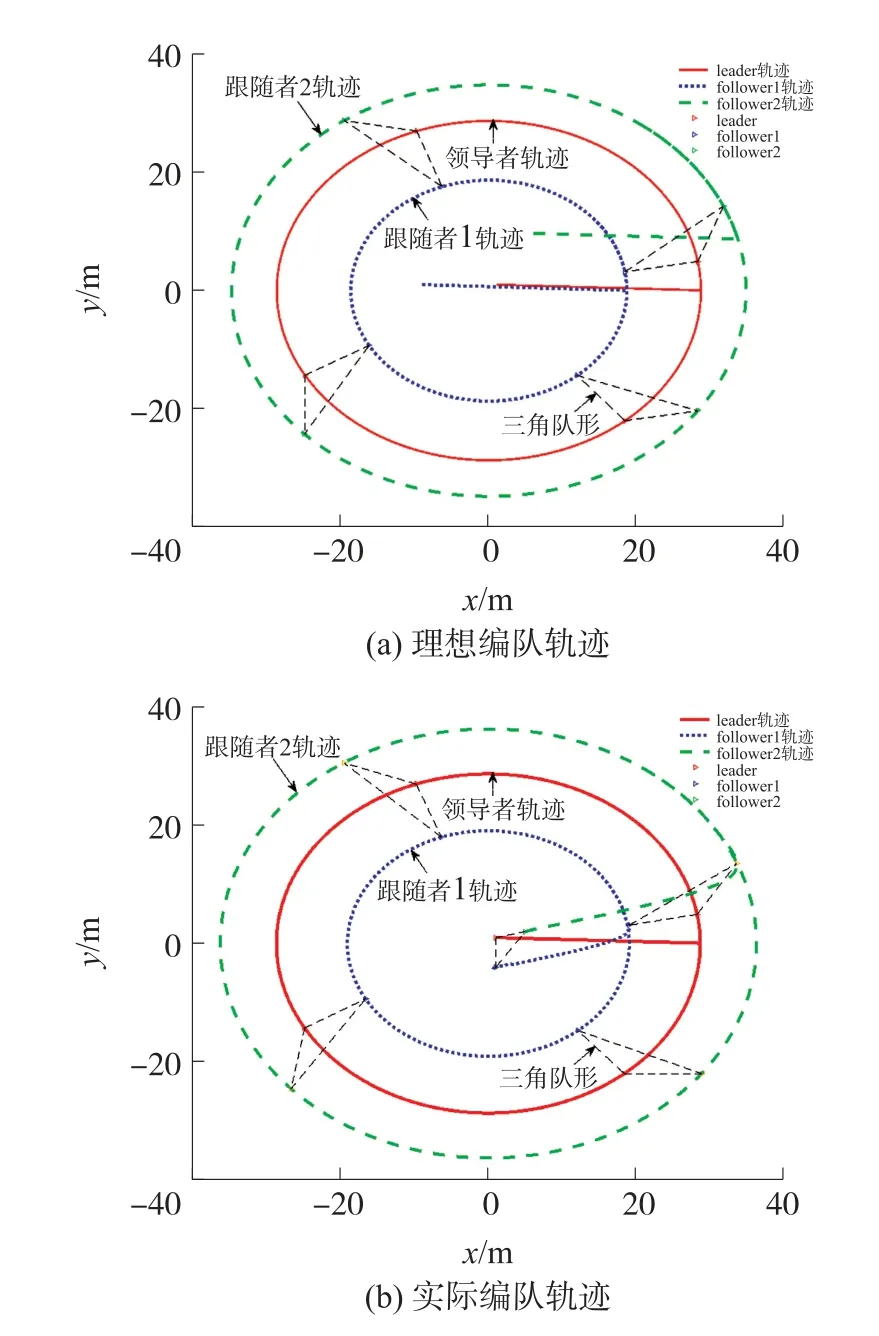
图4 仿真轨迹图

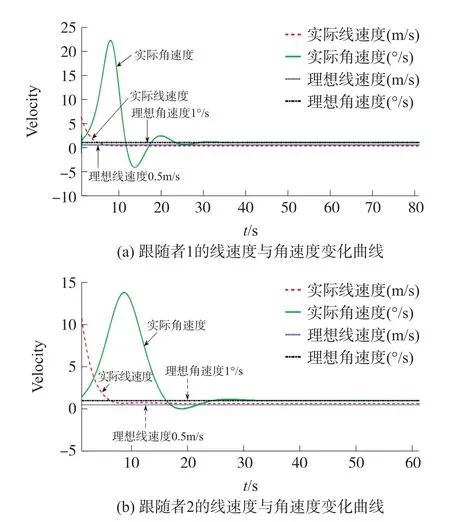
图5 跟随者AUV线速度与角速度

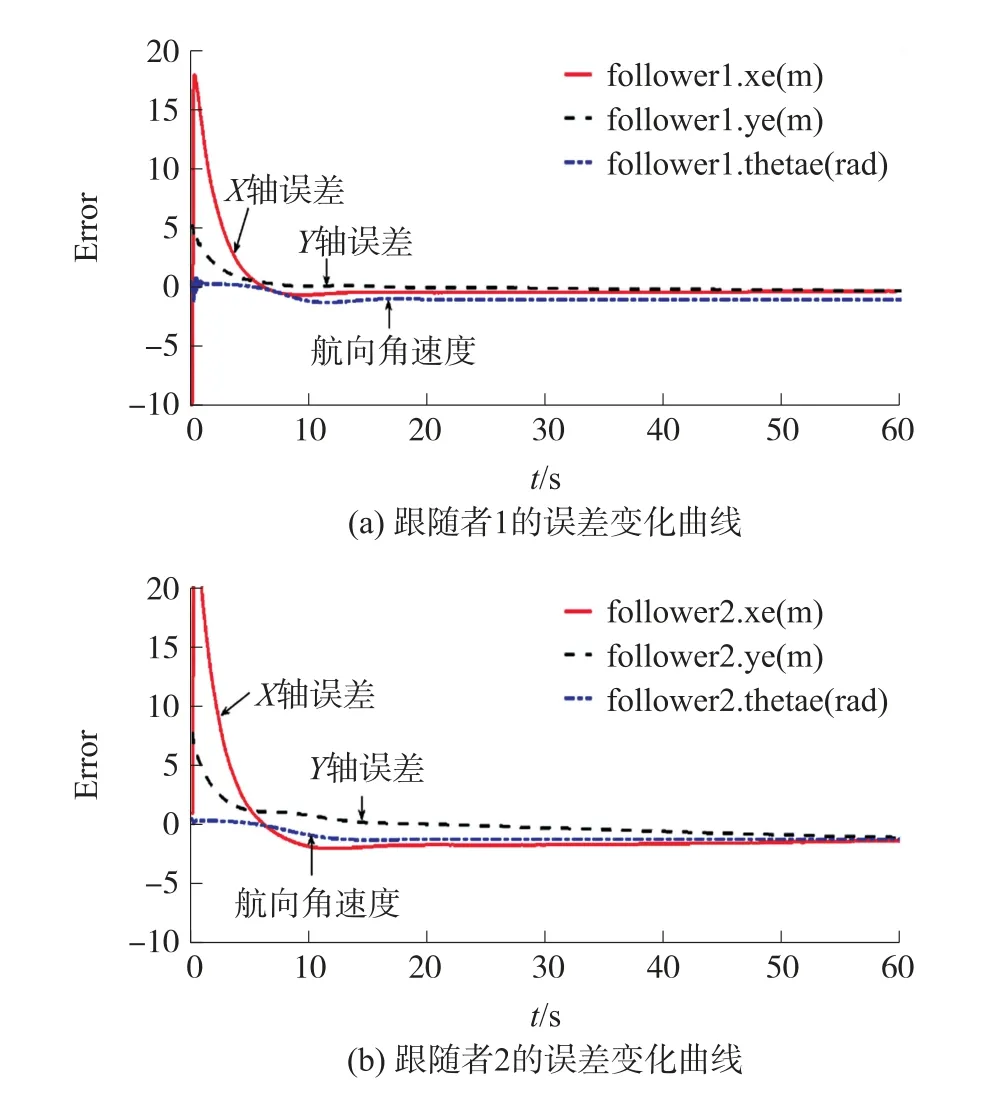
图6 跟随者AUV的误差曲线

从图5和图6的仿真结果图中可以看出两台AUV的线速度和角速度随着时间变化逐渐趋于稳定。除了在编队初始时刻的位置误差较大，随着编队过程的推进，跟随误差也渐渐趋近零，验证了本文提出控制律能够保证良好的编队队形。

4 结语

针对水下环境的特点与实际编队控制需求，本文提出了一种新型的主从架构下多水下机器人编队控制算法。对于AUV的非线性系统，采用反步法的思想与李雅普诺夫理论设计了新型的控制律函数，并证明了其收敛性。仿真结果表明本文提出的编队控制策略能够满足AUV编队的需要。后期研究将水声通信的延时约束引入到控制律的设计中，并利用真实AUV集群系统进行算法验证。