基于模型预测的自动驾驶横向控制算法研究

邢斯琦，冯 凯，薛玲玲

（陕西重型汽车有限公司，陕西 西安 710200）

前言

自动驾驶主要分为环境感知、决策规划和车辆控制三个部分，为了提高无人驾驶车辆系统的实时性，通过车辆动力学模型等效约束转化可以有效减少规划和控制的计算复杂度，提高系统的实时性。对于无人驾驶车辆来说，实现智能化和实用化的必要条件是高效稳定的轨迹跟踪控制[1]。本文研究的对象和问题是在常规道路环境下如何通过无人驾驶车辆的前轮主动转向实现轨迹跟踪控制。

1 Trucksim 车辆动力学建模

本文利用Trucksim 建立车辆动力学模型进行被控对象的相关仿真，根据实际车辆的真实尺寸参数、空气动力学参数、悬架的相关结构参数、轮胎参数等数据，建立需要的车辆动力学模型，Trucksim 界面及参数配置图如图1 和图2 所示，参数设定参考国内某重型牵引车（不包含牵引车后挂）。

图1 Trucksim 界面展示图

图2 Trucksim 参数配置图

1.1 控制算法简介

模型预测控制是一种反馈控制算法，使用模型来预测过程的未来输出，解决带约束的优化，最终求得最佳解作用于控制系统[2]，其中的滚动优化和反馈校正特性，可以减少系统滞后导致的误差，提高控制系统的性能，达到优化的目的。

其主要特点是：

（1）支持多输入/输出系统，以便能够建立起输入输出之间的相互影响参数。

（2）支持添加多项约束条件。

（3）预测功能，即预测出未来时刻系统的输出以达到控制当前系统状态的目的。

（4）反馈校正和在线优化，利用输出的实时控制信息对基于模型的预测结果进行误差校正后，在线进行下一次的优化，以此反复。

模型预测控制算法主要分为三个部分：模型预测、滚动优化和反馈校正。经典的模型预测控制算法控制流程如图3所示。

图3 模型预测控制算法结构图

模型预测是算法的基础，它可以根据被控对象的历史信息和未来输入，预测出控制系统未来某一时刻的输出[3]。而且该算法对预测模型的类型也没有严格的限定，状态方程、传递函数等常用的传统模型都可作为算法的预测模型。

在实际控制过程中，控制效果会受到很多环境因素的干扰，而模型预测控制算法中的滚动优化可以很好地抑制外部干扰产生的影响。该算法能够根据当前时刻重新建立预测时域内的目标函数，并且这种优化不是单次离线进行的，而是通过反复在线优化得到的。因此，滚动优化是模型预测控制算法区别于其他最优控制算法的根本点。

在实际情况中，控制效果除了会受到外部干扰以外，还会出现模型预测值与实际不相符，出现较大偏差等现象。所以利用模型预测控制算法的闭环优化特点，通过输出值与模型的预估值进行比较，使用得出的误差来矫正模型的预测值，进而得出未来时刻更为准确的预测值。这种闭环控制的优点，可以使模型预测控制算法的抗干扰能力得到很大提升。

1.2 控制算法基本原理

模型预测控制算法的基本原理如图4 所示。

图4 模型预测控制算法基本原理图

整个控制过程满足上述的三要素，始终会存在一条期望的参考轨迹，以k 时刻作为当前时刻，控制系统会根据当前测量值和预测值，预测未来一段时间内系统的输出，通过求解满足约束条件的目标函数最佳解，得到该时域内的控制序列，但只需将该控制序列中的第一项元素作为受控对象的实际控制量，下一时刻，反复如上的预测动作和控制行为，逐步完成满足约束条件的优化求解问题，这样就实现了对被控对象的持续预测控制功能。

2 模型预测控制算法仿真

2.1 建立预测模型

本文在车辆运动学建模之前先对车辆进行简化，将车辆抽象为前后两个车轮，即使用简单的自行车模型[4]。如图5所示，使用车辆的前后轮和车轴来表示，车辆轴长表示为d，前轮转角表示为θ，车辆在进行转弯的动作可以近似简化为车辆后轴绕某一点做圆周运动，转弯半径可表示为该圆周的半径长度r，通过三点形成的三角形可以推导出车辆航向角度的变换为车辆行驶的距离除以转弯半径r，对时间的一阶导数即为航向角的角速度，基本推导结果如式（1）所示。

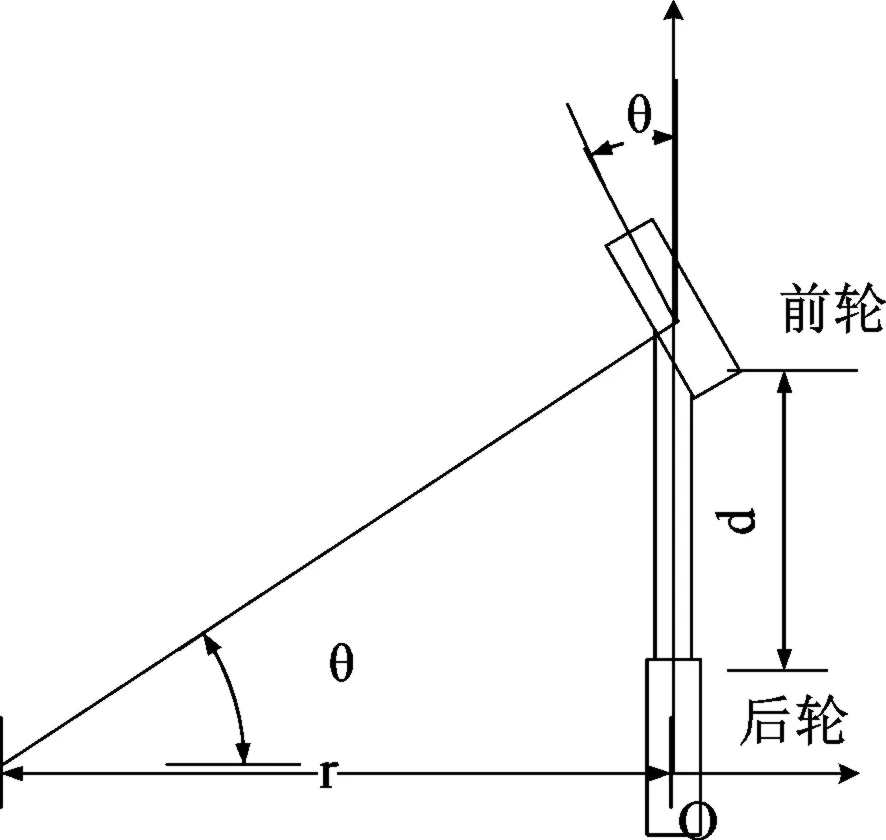
图5 简单自行车模型结构图

当前航向角的角速度可以表示为：

式（2）中：v为车辆当前速度；r为转弯半径。

以车辆后轴中心为原点O 建立直角坐标系，车辆纵向速度、横向速度和航向角速度可以用状态方程表示如下[5]：

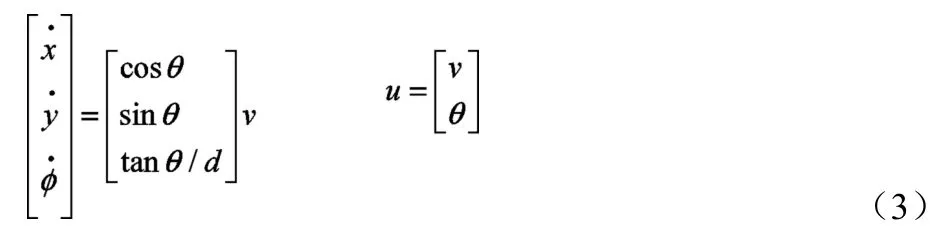
式（3）中：φ为车辆当前航向角；x、y、φ为状态变量；v、θ为控制变量。

当已知车辆速度为v，车轮转角θ 时，可根据上述公式得到车辆的位置x、y和车辆转向角φ。

因为状态方程是一个非线性的方程，所以需要先进行线性化，再对已经生成路径上的某一点进行泰勒展开，取第一阶即完成了整个线性过程。那么系统的状态方程可以转换为如下式（4）。

式（4）中：A(t)为f(x,u)对x的雅克比矩阵；B(t)为f(x,u)对u的雅克比矩阵。则转化结果对应的雅克比矩阵AB 分别如下所示：

为了对达不到目标条件的车辆模型施行“惩罚”[6]，需要尽可能抑制误差，并且根据需求不同损失项的选取也不一样，对于这些损失项需要用权重系数加以区分，设置损失函数和限制条件如式（5）。

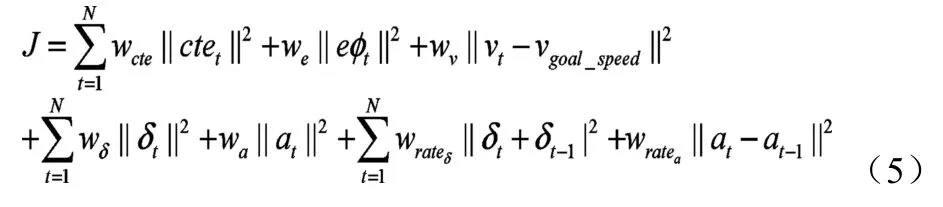
控制量约束条件：

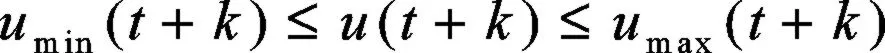
控制增量约束条件：

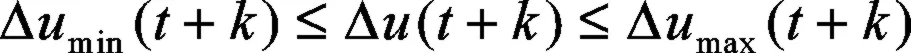
输出约束条件：

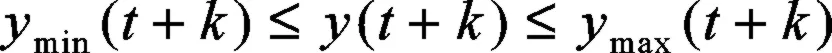
2.2 仿真结果

利用MATLAB/Simulink 的仿真模块对该算法进行仿真模拟，在Trucksim 中搭建车辆动力学模型，并完成对于Simulink 的输入输出对应设置，然后在Simulink 中设置S 函数实现控制算法[7-8]，模块封装结构如图6 所示。最后运行搭建的仿真模型，在Trucksim 中动画展示中可以看到车辆各参数变化情况，包括车轮转角变化曲线、车速变化曲线、横向加速度变化曲线等，如图7 所示。

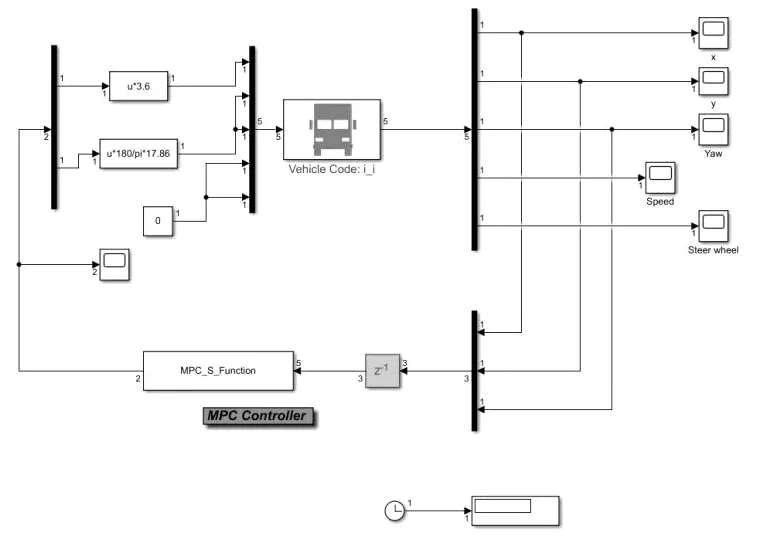
图6 Simulink 模块封装结构图

图7 Trucksim 仿真效果示意图

3 结论

模拟仿真测试验证表明，在理想情况下模型预测控制算法能够快速且稳定地跟踪期望轨迹，但是在性能和效率等方面还需要进行算法优化。具体优化方向如下：

（1）目标函数约束选取。在进行实车综合项目开发时，根据实际要求进行约束条件的选取，避免因为约束条件少造成实际控制效果不好的问题。

（2）算法性能优化。算法需要实时计算，耗费系统资源大，后期可以对车辆动力学模型进行合理的简化，减少控制算法的在线计算量，从而减小系统的资源占有率。

（3）算法效率优化，提升实时性。通过采样周期的缩短保证实时控制，但是采样周期的缩短不能小于最长制动时间，这样会存在还未完成制动达到所需状态，已经进行了下一次采样和预测。