铁路货物运输网络关键节点识别算法研究

刘 杰

(重庆工程职业技术学院 智能制造与交通学院，重庆 402260)

0 引 言

铁路货物运输在物流快速发展的今天扮演越来越重要的角色。在中国，铁路占整个货物运输比重的8%，是全国货物运输的重要组成部分。货运车站和铁路线路构成一个庞大的铁路货物运输网络。货运车站作为网络中的节点，研究其重要度并找出关键节点对于有效保护铁路运输网络安全并进一步保证货物运输流程通畅具有现实意义。

文献[1]和文献[2]分别于1998年和2000年提出小世界网络和无标度网络广泛存在于现实世界，掀起了用复杂网络理论对网络关键点研究的热潮。关键节点重要度识别方法多以网络自身属性[3]如度[4]、介数[5]和网络效率[6]等为量化测度标准来评价网络节点。交通研究领域主要集中在城市轨道交通拓扑结构、铁路客运网络和城市道路网络方面。薛锋等[7]利用复杂网络理论分析了成都地铁网络拓扑结构，然后构建节点重要度评价指标体系并结合TOPSIS方法完成关键节点识别任务；谌微微等[8]构建基于二阶张量的重庆轨道交通线网拓扑模型，然后用3个中心性指标评价网络节点，结果表明，五里店、重庆西、沙坪坝和冉家坝4个站点最为关键；刘朝阳等[9]建立了城市轨道交通网络级联失效模型，并以网络失效规模和破坏程度两个指标对其进行评估，最后通过仿真找出网络中的关键节点；陈钉均等[10]在建立铁路网客运节点指标体系基础上，利用粗糙集理论和主成分分析法计算客运节点综合权重，结果表明其评判结果有效；邓红星等[11]选用节点度、介数和站点客流集散量等7个指标构建节点重要度评价体系，对哈尔滨市区道路网进行实证研究，结果表明，其关键节点识别方法可行且有效；毛剑楠等[12]在城市基础经济属性、公路与铁路客运拓扑网络属性和城市联系强度属性基础上，提出一种城市群综合节点重要度计算方法，以四川城市群为实证研究对象，结果表明该方法有效；宋海权等[13]定义道路重要度评价模型，并顾及路网的整体形态及路网的拓扑连通性，提出基于复杂网络理论的路网综合算法，对成都道路网络实证研究结果表明该模型有效； ZHU Yanbo等[14]以图论为基础对丝绸之路经济带铁路网络节点重要度进行研究，利用pajek软件仿真发现了其中3个最关键节点。

目前专门针对铁路货运网络关键点识别的研究较少，仅有SUN Qipeng等[15]基于复杂网络理论对中国铁路货物运输网络进行研究，以各省份为网络节点、省间货物运输重量为边进行建模，最后得到各节点重要度并分析了其影响因素。然而该研究只讨论了以省份为节点的宏观网络，没有重点讨论以车站为节点的微观网络。人们对车站重要度更为关切。铁路部门目前实际的做法是在分析车站客运量、货运量和地理位置等因素基础上，将货运站划分为6个等级，但这种划分方式有很强的人为主观性且无法量化。铁路货物运输网络的核心在于货物的运输特性，而不是线路的拓扑结构。货运站每天货物承运和卸货情况不相同，车站间发送货物的种类、重量也不相同。除此之外，货物的价值也是一个影响关键节点识别的重要因素。显然接收和发送货物重量少但货物总价值更高的车站比发送货物重量高但价值低的车站更为重要，这是以往研究所没有考虑的。因此笔者以货物总价值为标准进行铁路货物运输网络节点重要度计算和关键节点识别研究依据。鉴于铁路货运网络中的这种货物动态转移特性，笔者采用PageRank算法对铁路货运站重要度进行计算并识别关键点[16,17]。

1 研究方法

从微观角度看，铁路局所属车站每天发送和接收的货物运量也不尽相同，如图1。

图1 独山站货物运量Fig. 1 Dushan Station freight volume

笔者从两个方面定义货运车站重要度：一方面是货运站的货物发送和卸载业务量，业务量越大，重要度越高；另一方面是与货运站有直接业务往来车站性质，往来车站越重要，本站重要度也越高。由于货运车站间的货运业务每天都在变化，同时存在一些不可控外在因素的干扰，故货运车站每天的重要度可能都不一样。因此，笔者定义货运车站重要度为一个随机变量，通过重要度算法算出车站每天的重要度构成的随机变量样本序列，然后拟合随机变量的分布函数。基于车站间货物运输信息，可以通过PageRank算法计算得到车站每天的重要度。

基于PageRank算法计算货运车站重要度，其核心思想是将车站抽象为图的节点，车站间货运业务抽象为边，货物运输网络抽象为马尔可夫概率状态转移矩阵，最后采用迭代计算得到稳定解:

(1)

式中：A为概率状态转移矩阵；m为迭代次数；x0为节点初始重要度向量；x为最终节点重要度向量。

(2)

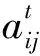
(3)

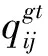
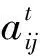
图2 独山站货物价值Fig. 2 Value of goods at Dushan Station

(4)

式中：pg为第g种货物价格；S为车站集合。

得到重要度样本后，拟合各车站重要度分布函数，最后根据重要度分布函数的期望特征值计算最终的重要度数值。

2 模型建立

2.1 PageRank 算法

为了使式(2)中At在迭代中收敛，需要对原PageRank算法做出一些修改，具体算法如下[18]：

Step 1构造货物转移矩阵At，给定误差阈值ε。

Step 2向该矩阵中添加虚拟节点(即设置一个虚拟车站)，该节点与其他节点双向连接，得到新矩阵：

(5)

Step 3计算转移概率，得到概率转移矩阵：

(6)

Step 4设初始状态各节点重要度为[1，1，…，0]1×(n+1)(虚拟节点重要度为0)，m=0，转Step 5。

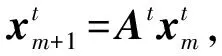
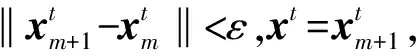
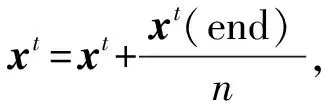
2.2 拟合分布模型选择

有限高斯混合模型在理论上被证明可以以任意精度正逼近实数上的非负黎曼可积函数，特别可以逼近任意的概率密度函数[19]：

(7)

(8)

式中：wk为第k个单正态分布权重值；μk为第k个单正态分布均值向量；Ck为第k个单正态分布协方差矩阵；d为变量维度；K为单正态分布函数总个数。如果x为单变量，则式(8)变为：

(9)

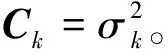
高斯混合分布模型参数估计通常采用EM迭代算法，EM算法分为两步，第一步称为E-Step：

(10)

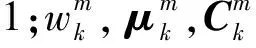
为叙述方便，整个GMM模型参数记为：

(w,μ,C)=[(wk,μk,Ck),k=1,2,…,K]

(11)

第二步称为M-Step,其目的是最大化Q函数，如式(12)，从而得到第m+1次迭代模型参数，如式(13)：

(12)

wm+1,μm+1,Cm+1=argmaxQ(w,μ,C,wm,

μm,Cm)

(13)

对Q函数求导并令导数为0，可得：

(14)

(15)

(16)

重复上面第一步和第二步，直到收敛为止。

2.3 重要度计算

得到重要度分布函数后，取其均值作为车站重要度的度量，如式(17)：

(17)

3 实例分析

数据来源于中国铁路货物全过程管理系统，从系统中导出中国铁路成都局集团有限公司最近一年(即从2018年1月1日到2019年1月1日)的数据，提取其中194 d的货运记录观察数据。一个车站一天货运数据包含于承运簿和卸货簿两个EXCEL文件内。承运簿记录的是该车站发往其他车站的货物情况，内容有时间、发送目的地车站名称、货物名称、计量单位和货物重量。卸货簿记录的是其他车站发到本站的货物情况，内容有时间、货物来源车站名称、货物名称、计量单位和货物重量。笔者利用Python 3.7编程对数据进行处理[20]。经统计后得到中国铁路成都局集团有限公司管辖货运车站共115个，中国铁路成都局集团有限公司与其他省市路局有货运业务的车站总数为1 900个，因此模型参数取值为n=2 015，H=|T|=194，|G|=1 538，ε=10-6，K=30。另外，在统计中发现货物中有用数字命名的军用物资，比如14/65 658、18/63 678等。军用物资涉及机密，无法知道其种类。但对于此类货物，笔者认为其价值非常高，以一个较高单价进行计量。

根据2.1节设计的算法计算得到各车站重要度情况如图3(仅列出5个车站重要度变化情况)。按式(16)计算得到的中国铁路成都局集团有限公司车站重要度结果如图4。

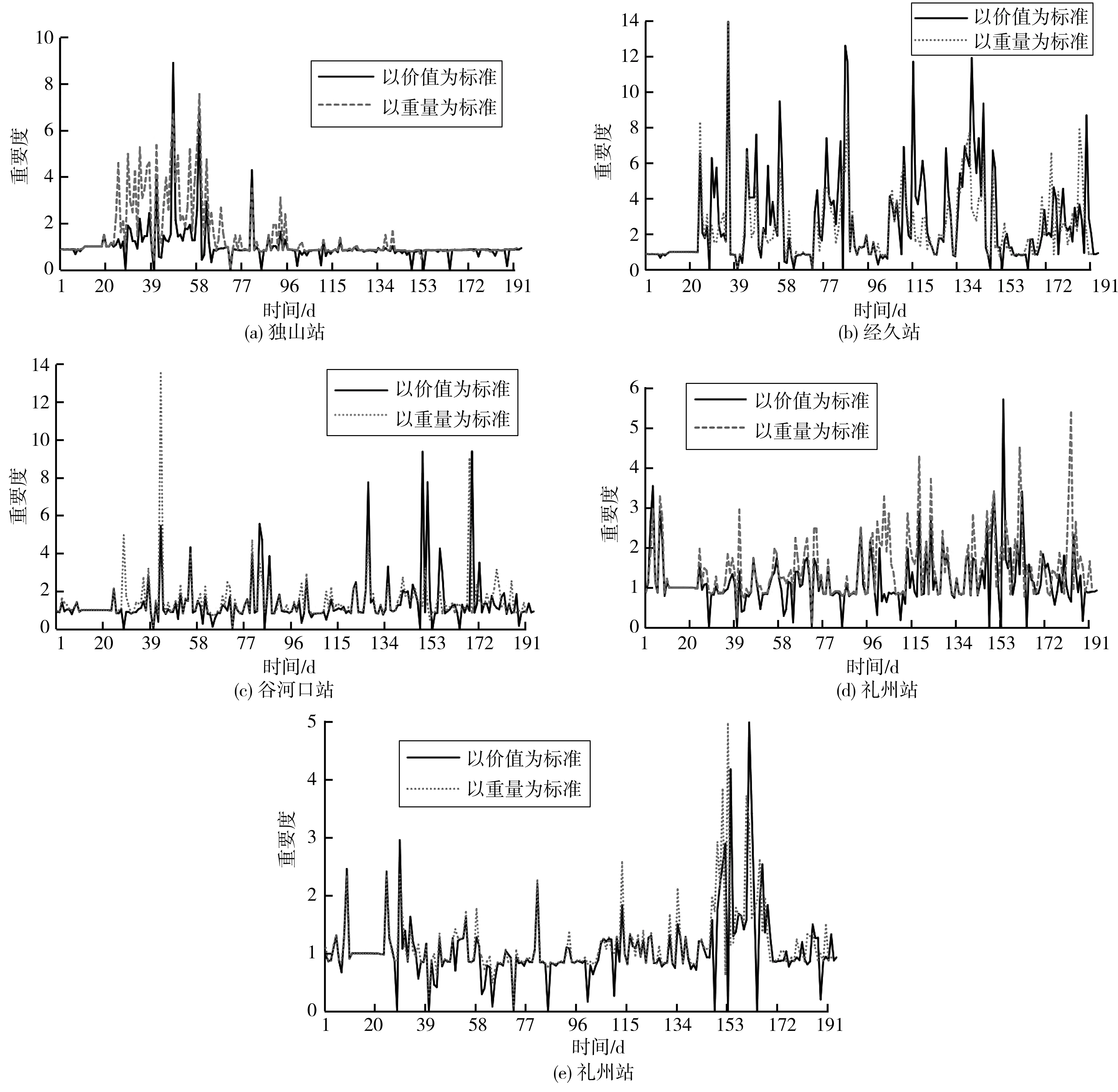
图3 各车站重要度时间序列变化情况Fig. 3 Time series changes of station importance

图4 车站重要度对比Fig. 4 Comparison of station importance

从价值标准来看，重要度前十名分别是小寨坝、彭县、福泉、铜罐驿、巴关河、鱼嘴、凯里西、广安、新兴镇、渡口，其重要度值分别为118.28、31.1、28.87、24.54、18.45、13.23、13.04、11.69、11.46、10.46。一、二、三、四等站平均重要度分别为4.59、2.99、4.24和2.76，成都局一等站只有攀枝花站，三等站共42个，这说明三等站是整个货运网络中货运重要性最高的车站集群，对三等站的保护尤其重视。从重量标准来看，重要度前10名分别是小寨坝、铜罐驿、彭县、弄弄坪、巴关河、广安、福泉、攀枝花、渡口、燕岗，其重要度值分别为62.27、14.07、13.55、13.15、11.8、10.86、10.69、9.86、9.56、8.42。一、二、三、四等站平均重要度分别为9.86、2.41、3.03和2.34。从两个标准来看一等站和三等站均为货运网络的关键集群车站。小寨坝又是整个网络最核心节点。通过分析承运簿和卸货簿发现，排名靠前的车站如鱼嘴、凯里西、新兴镇等虽然货运量大，但是货物价值并不高，而小寨坝、彭县、铜罐驿除货运量大外，周转货物主要是高价值集装箱或军用物资，这也说明了导致两种标准差异性的原因，亦证明了结论的有效性。

4 结 语

笔者利用铁路货物全过程管理系统数据对中国铁路成都局集团有限公司管辖的115个货运车站重要度进行计算，结合PageRank算法、数据分布拟合理论计算得到了以价值和重量两种标准下的车站重要度，同时发现了少数重要度很高的节点，这表明货运网络从运输角度来看亦是一种具有少数中心节点的复杂网络，因此对这些中心车站实施重点保护和监控尤为重要。