基于演化博弈理论的城市轨道交通高峰票价定价研究
2021-08-27焦柳丹朱影含宋向南
焦柳丹,朱影含,吴 雅,宋向南
(1. 重庆交通大学 经济与管理学院,重庆 400074; 2. 西南大学 资源环境学院,重庆 400715;3. 广州大学 管理学院,广东 广州 510006)
0 引 言
城市轨道交通是解决城市交通拥堵,提高城市公共交通出行服务水平的有效手段之一[1]。在过去10年间,我国城市轨道交通建设取得了巨大的成就。截至2018年末,我国内地已开通运营城市轨道交通线路的城市共计32个,运营线路总长度达到5 123.3 km,累计开通运营线路153条,运营车站3 255座[2]。然而,城市轨道交通在快速发展的同时,其客流量也在急速增长,相关线路运输能力趋于饱和,给城市轨道交通的运营管理带来了新的问题和难题[3]。其中,早晚上班高峰时段超负荷的客流强度,会导致在车站站台和车厢内通常集聚了大量的乘客,从而引起的拥挤问题在各大城市日益突出[4]。而城市轨道交通拥挤问题,不仅会降低乘客的舒适性,还会带来诸多如火灾、踩踏事故等安全风险隐患[5]。另一方面,乘客在选择城市轨道交通出行过程中,不仅受到城市轨道交通自身服务质量,如便捷性、快捷性、经济性等多种因素的影响,还会对其他交通方式如地面公交、出租车等进行比较选择。因此,在综合考虑乘客出行选择的情况下,合理降低城市轨道交通运营拥挤情况,从而提高城市居民出行质量,对于促进城市轨道交通可持续发展显得十分重要。
伴随着城市轨道交通客流拥挤问题不断凸显,如何降低其拥挤程度水平开始受到广泛关注。其中,利用“削峰填谷”思想,对城市轨道交通的票价进行分时定价,被认为是一种降低城市轨道交通拥挤情况的管理方法和措施[4,6,7]。城市轨道交通分时定价,是针对轨道交通不同的运营时段制定不同的价格,利用乘客对票价的敏感性,引导乘客错峰出行[6]。相关学者已针对城市轨道交通分时定价问题展开了一系列的研究。例如,李静等[7]通过结合北京城市轨道交通的实际数据,对不同时段、不同票价下客流转移比率、地铁满载率等指标进行Agent 建模分析,并建议在非高峰时段应收取低于3 元的平均票价,而在高峰时段则收取高于7元的平均票价;付聪等[8]基于最优拥挤定价理论,探讨了天津市城市轨道交通拥挤定价的收费标准;田贵超等[9]根据上海市城市轨道交通的实际情况并结合乘客行为与调查结果,提出了时间差别分时定价策略;秦华容等[10]则以宁波市为例,通过测算私家车出行成本,结合公交车票价、利用弹性原理确定了城市轨道交通的合理定价区间,并提出了相应的保障措施;王健等[11]则根据城市轨道交通不同时段的客流特点引入了时间权重系数,在拉姆塞定价理论的基础上分析建立了城市轨道交通的多时段定价模型;张爱琳等[12]从票价收益和拥挤定价两个角度,综合运用了数据挖掘和SP 调查法,构建了基于人工智能系统Agent仿真模型的地铁分时定价机制;Z.WANG等[13]认为提高城市轨道交通票价可以缓解车厢拥挤的同时,也可能导致城市轨道交通客流流失。因此,以北京城市轨道交通为例,探寻了票价上涨高、中、低3种情况下对客流量的影响进行了分析;H.YANG等[14]针对城市轨道交通高峰期客流拥挤问题,提出了一种客票奖励方案,即乘客在高峰时段进行一定次数的出行后,可以在平峰时段免费乘车一次,从而改变通勤者的出发时间;Q.ZOU等[15]探寻了城市轨道交通高峰前票价降低对乘客出行时间的影响,指出不同乘客群体对票价折扣的影响存在较大差异,其中采用轨道交通出行频率较低的乘客比频率较高的乘客其票价敏感性更高。
然而,城市轨道交通票价制定的影响因素众多,主要包括相关运输成本、市场需求、乘客支付能力以及外部竞争等方面[16]。其中,城市轨道交通与地面公交是我国主要的两种公共交通方式,通过合理分配城市轨道交通与地面公交之间的客流,从而降低轨道交通拥挤程度具有重要意义。同时城市轨道交通与地面公交之间具有一定的竞争关系[17]。也有学者指出,我国目前城市轨道交通票价较低,本该承接地面小汽车出行量的城市轨道交通成为了地面常规公交的竞争者,地面小汽车的数量不减反增,不仅没有减轻道路拥堵情况,反而一定程度上加剧了城市轨道交通的拥挤状况[18]。因此,在制定城市轨道交通分时定价策略时,还应考虑城市轨道交通与地面公交的时间、空间价值,确立合理的城市轨道交通高峰票价,以确保其与地面公交客流的相对均衡性,以发挥二者的最大价值。有关学者在这一方面进行了相关尝试。例如,韩冰冰等[19]采用博弈模型分别对城市轨道交通和常规交通在4个阶段即引入期、成长期、成熟期和衰退期的竞争关系做了描述和分析,最终得到合理的票价方案。谭金会等[20]通过建立地铁与公交的两方动态博弈模型求得均衡票价以确保地铁、公交、居民三方利益的最大化。但通过对有关文献进行梳理总结发现,利用分时定价策略,综合考虑地面公交因素,合理确定城市轨道交通高峰票价,从而降低城市轨道交通拥挤状况的研究相对较少。基于此,通过构建群体成员高峰时段对于城市轨道交通以及地面公交选择情景下的演化博弈高峰票价定价理论模型,并以重庆市为例进行实证分析,以期为促进我国城市轨道交通可持续发展提供相关政策建议和决策支撑。
1 演化博弈理论模型构建
1.1 演化博弈理论
黄凯南等[21]在其研究中介绍到,演化博弈理论的形成与发展大致经历了3个阶段:首先,生物学家从博弈论在经济学中的运用得到启示,通过博弈论中策略互动思想建构了各种生物竞争演化模型;随后,生物学家根据生物演化的自身规律,通过引入生物适应度函数、突变机制以及选择机制正式形成演化博弈理论;最后,经济学家反过来借鉴生物学家的思想,通过随机稳定均衡以及随机个体学习动态模型进一步推动演化博弈的发展。演化博弈论将博弈理论与动态演化过程相结合,采用动态系统方法分析不完全信息演化的稳定性,已被应用于各个领域两个群体4种策略之间的研究,如政府与企业之间为探究合理环境税收的演化博弈模型[22]、供应商和制造商减排投入的演化博弈模型[23]、地方政府在是否执行环境规制情景下的演化博弈模型[24]。具体而言,博弈分析的目的是通过建立一定的机制和规则,达到理想的稳定均衡状态[25]。而通过构建城市轨道交通高峰时期票价定价博弈模型,进而分析城市轨道交通与地面公交之间的博弈关系,从而促使二者之间承担的客流量趋于均衡。相较于其他博弈方法,在个体有限理性的基础上,演化博弈理论更便于研究选择策略的整体变化趋势以及掌握网络动态的稳定性。因此,笔者基于群体成员高峰时段对于城市轨道交通以及地面公交选择的情景,进行了演化博弈模型的建立,从一定程度上避免了完全理性状态下始终以个体利益或效用最大化为目标的条件,以更为现实地解释群体成员对于出行方式的选择,从而科学准确地提出城市轨道交通高峰票价定价建议。
1.2 模型构建
演化博弈构建过程中主要元素有:得益矩阵,指从支付表中抽象出来由损益值形成的矩阵,用于描述两个人或多个参与人的策略和支付的矩阵;复制动态方程,用于描述某一特定策略在一个种群中被采用的频数或频度的动态微分方程[26];进化稳定策略,即促使博弈方在复制动态过程中最终收敛形成稳态的思想。
1.2.1 基本假设
笔者针对于群体成员高峰时段在城市轨道交通与地面公交二者之间选择的模型构建过程做出如下假设:
1)群体成员是有限理性[24]的,即愿意为城市轨道交通支付更高价格,愿意为地面公交付出更多时间。
2)群体成员的数量足够大且满足在博弈双方同时选择城市轨道交通或地面公交时,会产生部分成员需要等待下一班车次的情况;当博弈一方选择城市轨道交通或地面公交,另一方选择不相同的出行方式,则不需要等待下一班车次。
3)在出行过程中,不考虑城市轨道交通与地面公交到达同一目的地的出行距离差异,也不考虑同一出行方式的多种选择性。
1.2.2 得益矩阵
该博弈是群体成员随机配对形成两个群体所进行的博弈,博弈双方的策略均为选择乘坐城市轨道交通或者选择乘坐地面公交,故该博弈是2×2的对称博弈。假设群体1在群体2选择城市轨道交通出行的情况下,自己选择城市轨道交通或地面公交出行的收益分别是A11以及A21;在群体2选择地面公交出行的情况下,自己选择城市轨道交通或地面公交出行的收益分别是A12以及A22。
出行收益主要考虑时间成本(C×T)以及票价成本P即A=-C×T-P,时间成本包括车外时间成本以及车内时间成本A=-(CoTo+CiTi)-P,车外时间包括步行时间以及等车时间,因此最终的出行收益可表示为[17]:
(1)
式中:Co为步行和候车的时间价值;Ci为行车的时间价值;Di为两种出行方式平均站间距;vb为步行的速度;vi为两种出行方式的行车速度;fij为4种策略下的候车时间;L为行车距离;Pi为两种出行方式的票价。
(2)
同理,A12,A21,A22均可表示为:
(3)
(4)
(5)
式中:f1和f2分别为城市轨道交通以及地面公交高峰时段发车频率。
因此,群体成员随机配对形成两个群体对于城市轨道交通以及地面公交选择的对称博弈得益矩阵如表1。
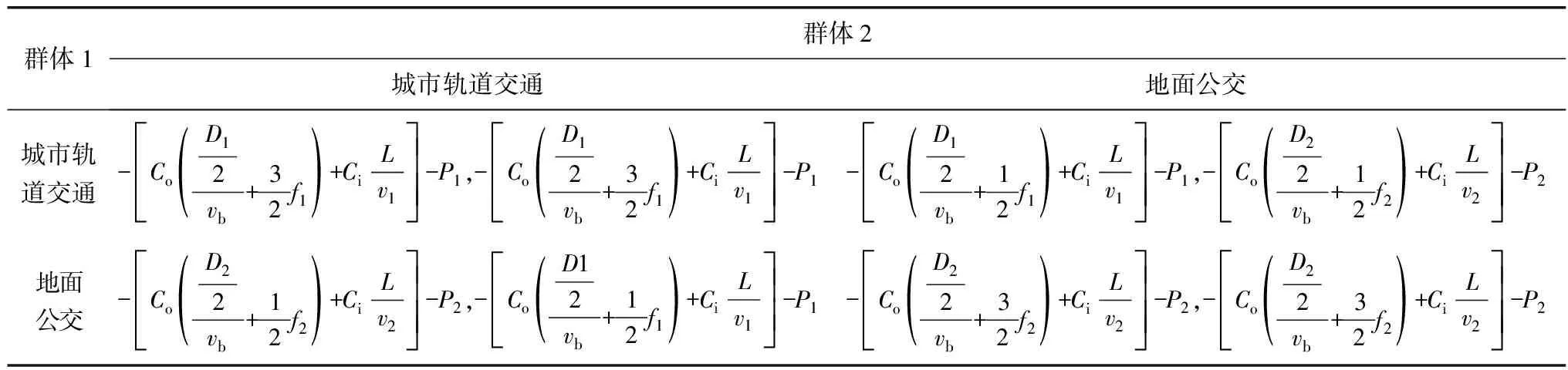
表1 两出行方式的得益矩阵Table 1 Benefit matrix of two travel modes
1.2.3 复制动态方程
假设选择城市轨道交通出行的群体比例为X1,选择地面公交出行的群体比例为X2=1-X1,那么某人选择城市轨道交通或者地面公交的期望收益为:
(6)
(7)
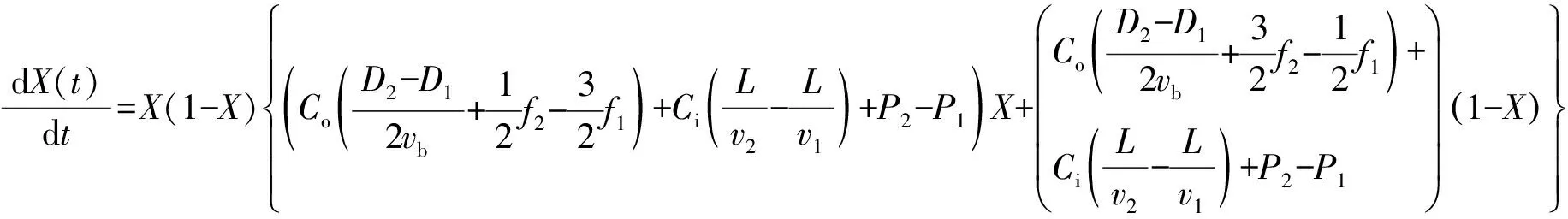
(8)
1.2.4 进化稳态

(9)
(10)
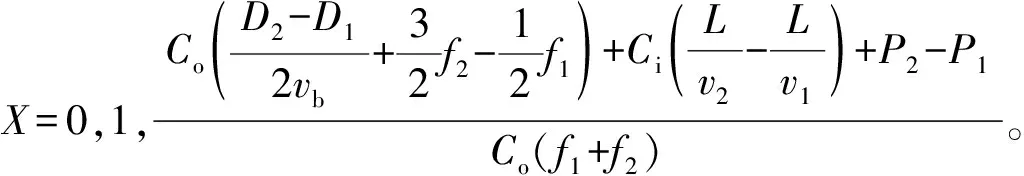
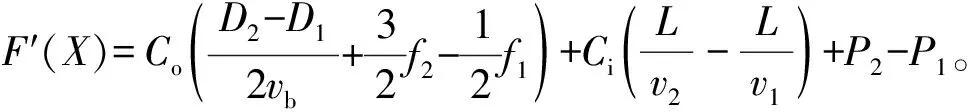
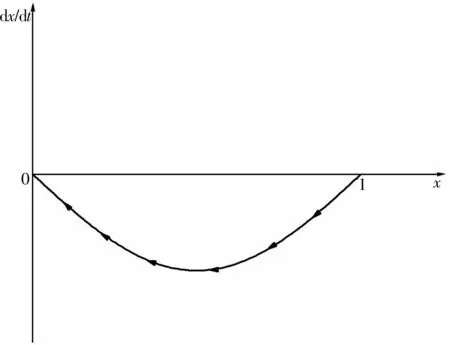
图1 动态相位(X=0)Fig. 1 Dynamic phase diagram(X=0)
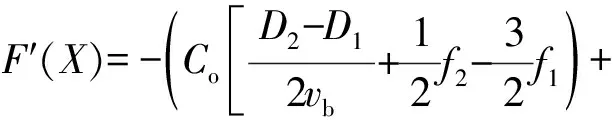


图2 动态相位(X=1)Fig. 2 Dynamic phase diagram(X=1)
3)当X=

F′(X)=

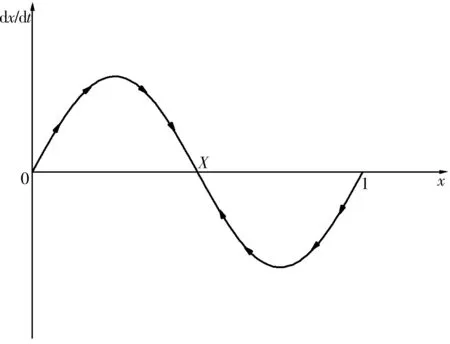
图3 动态相位(0 故该博弈模型城市轨道交通出行比例最终演化稳定状态可表示为: (11) 重庆市作为西部大开发以及长江经济带的重要支点,其经济在近年来发展迅速,大量的人口流入以及日益增加的私家车数量给地面交通以及城市轨道交通都带来了一定的拥堵情况。根据《城市轨道交通2018年度统计和分析报告》相关数据显示,重庆市2018年城市轨道交通线路总长达313.4 km,高峰小时断面客流量最高为3.75万人次,重庆市城市轨道交通快速发展的同时,高峰时段轨道交通站点以及列车内拥挤现象严重[4],极大地降低了乘客的安全性以及舒适度。根据《2018年度中国主要城市交通分析报告》显示,重庆市2018年高峰行程延时指数为1.890,位居全国第4,地面交通状况糟糕加剧了城市轨道交通客流集聚,地面公交空间价值未能有效利用。因此,以重庆市为例,采用所构建的演化博弈模型对城市轨道交通票价定价以及客流敏感性进行了分析。 根据《城市轨道交通2018年度统计和分析报告》,重庆市城市轨道交通平均旅行速度为40.9 km/h;根据《2018年度中国主要城市交通分析报告》,重庆市地面公交平均巡航速度为17.5 km/h;根据《2018重庆市主城区交通发展年度报告》,城市轨道交通线路高峰小时平均发车间隔为4 min,平均站点间距为1 750 m,票价按公里计算;结合重庆市公交线路数据,地面公交平均发车间隔为10 min,平均站点间距为740 m,票价为2元。 根据《2018年重庆市国民经济和社会发展统计公报》,2018年重庆市城镇居民人均可支配收入34 889元,故重庆市出行者的时间收入约为16.5元/h。参考相关研究[27],将交通成本进行量化,计算得出步行和候车的时间成本Co=0.42元/min,行车的时间成本Ci=0.14元/min,同时取vb=4.4 km/h。根据《2018重庆市主城区交通发展年度报告》,目前城市轨道交通出行占公共交通出行的7/25,平峰时段城市轨道交通拥挤现象明显减少,地面公交空间价值也得到有效利用。故假设高峰时段城市轨道交通客流量占公共交通总客流量的7/25为此时的稳态,根据博弈模型所给出的结果如表2。 表2 博弈票价对比Table 2 Game fare comparison 结果显示,原票价以2元为基础票价,以1元递增,在高峰时段博弈模型中,票价以4元为基础票价,以2元递增能够有效的让地面公交分担更多的出行从而减少城市轨道交通客流量以保证相对的安全性和舒适度。通过对高峰时段票价定价相关文献研究分析[7,8,11,28],高峰时段票价与平峰时段票价比值多在1.2~2.3之间,本研究中演化博弈模型下高峰时段票价为平峰时段票价的2倍,研究结果与其他学者的成果基本吻合。 由表3可知,当票价下降20%,城市轨道交通客流占比将上升到0.43~0.76;当票价下降10%,城市轨道交通客流占比将上升到0.35~0.52;当票价上升10%,城市轨道交通客流将下降到0.04~0.20;当票价上升20%,城市轨道交通客流在出行距离在17 km之内将下降到0.02~0.12,而出行距离在17 km以上,城市轨道交通将面临无人乘坐的困境。将城市轨道交通客流变化幅度与票价变化幅度作点线图如图4。 由图4可知,从横向角度即相同出行距离的视角出发,票价幅度变化越大,客流量变化幅度也越大;从纵向角度即不同出行距离的视角出发,在相同票价变化幅度的情况下,出行距离越远,客流变化幅度越大,且随着出行距离的增加,客流变化幅度差值显著增加。由此发现,票价变化对于城市轨道交通客流量的影响较大,且出行距离更远,城市轨道交通客流对于票价的敏感程度越高。随着城市轨道交通线网不断的优化与完善,远距离出行乘客数量将会得到一定程度的增长,城市轨道交通客流对于票价的敏感程度也会越来越高,因此,未来对于高峰时段城市轨道交通票价的动态调控显得十分重要。 图4 票价变化幅度与客流变化幅度点线Fig. 4 Point chart of variation range of fare and passenger flow 通过构建群体成员高峰时段对于城市轨道交通以及地面公交选择情景下的演化博弈模型,对重庆市高峰时段城市轨道交通票价定价进行了研究分析,结果显示:当基础票价达到4元并以2元递增的情况下,城市轨道交通和地面公交会形成一个稳态即双方的客流量达到一个相对均衡的状态,双方不会出现过度拥挤的情况从而提升乘客舒适度同时降低安全隐患发生率,并能实现各自的时空价值。在该计算结果基础下,笔者针对高峰时段城市轨道交通客流量与票价进行了敏感性分析,结果显示:城市轨道交通客流量对于票价的敏感程度较高,同时,城市轨道交通票价越高,城市轨道交通客流量对于票价的敏感程度越高。 对研究结果梳理发现,通过提高城市轨道交通票价,从理论上能够有效的转移部分客流至地面公交从而达到有效缓解城市轨道交通拥堵的现象。然而,城市轨道交通票价变化对于客流量的影响较大,如何确定高峰时段票价的合理涨幅还有待进一步从乘客的主观意愿开展相应的研究。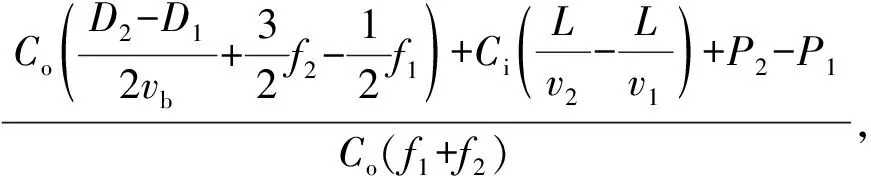
2 实证分析
2.1 重庆市公共交通高峰现状
2.2 重庆市轨道交通票价定价分析

2.3 重庆市轨道交通客流敏感性分析
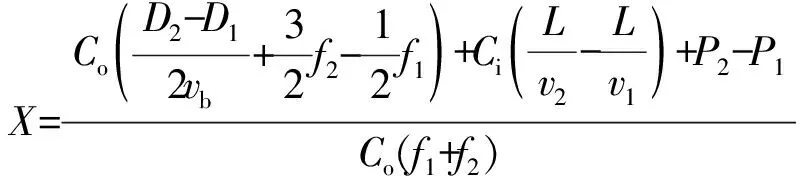

3 结 语
