ARMA模 型 和Holt⁃Winters指数平滑模型在企业用电量预测中的应用与分析

陈云浩，周 冬

（1.湖南天羽能源科技股份有限公司，湖南 长沙 410205；2.四川省社会科学院，四川 成都 610072）

1 问题提出

根据中共中央国务院《关于进一步深化电力体制改革的若干意见》（中发［2015］9号）及配套文件精神，在国家发改委、国家能源局的指导下，近年来各地加快推进电力市场化改革，提升市场主体竞争意识，释放改革红利，降低用电成本［1］。电力市场化改革给电力行业实施需求侧管理（DSM）带来了新的挑战，原有垂直垄断体制下实施DSM给电力公司带来的效益被分散，一些传统的DSM措施如负荷管理与能效提升的实施基础也发生了变化［2］。

因此，在电力市场化改革和电力需求侧管理的双轮驱动下，在国家节能减排重大战略实施的指引下，对大型工业企业、大型工商业用户的用电量预测逐步受到各个利益相关方的重视。没有准确的用电量预测，售电公司无法进行准确的销售报价或制定最优的批发购电价格策略，电网公司在开展需求侧管理、推广需求侧响应时，也无法制订有的放矢的方案和机制。特别是在电力现货交易的发展趋势下［3］，用电量预测已经从传统的宏观预测（地区、城市量级）和中长期预测（按年、按月）要转变为微观预测（按企业、按建筑）和短期甚至准实时预测（按日、按小时），对用电量预测方法和模型提出了非常高的准确度要求。

本文以中山市某工业企业逐日用电量数据为样本，用两种不同的模型分别进行预测，并验证模型的有效性，分析比较各自的特点。

2 现有研究成果综述

关于电量预测，较早前的研究大多数是国家电网、南方电网等电网公司以宏观用电量预测或者电力负荷预测为主，近年来也陆续有高校、设计院和节能公司针对大型公共建筑等用能单位开展用电量预测研究，但针对企业的用电量预测研究较少。

从分析对象的角度看，既有文献主要针对电力系统、办公建筑、商业建筑、地铁站等用能单位进行过用电量预测研究分析。例如江自强等提出了针对现代化建筑用电量的智能预测方法［4］，陈利芳提出了面向大数据的电力预测系统应用研究建议［5］，李龙、金樑等开展了短期电力负荷预测研究［6－7］，缪灵均等开展了生活能源消耗预测研究［8］，欧阳前武、刘晓婷等开展了大型公建能耗预测研究［9－10］，黄荣庚等开展了地铁站环控系统的能耗预测研究［11］。总体而言，既有研究工作还是以建筑类能耗的预测分析为主，对于工业企业的能耗预测分析较少。

从预测模型和方法的角度看，大多数文献提出了时间序列模型、多元回归模型、ARMA模型、指数平滑模型、神经网络模型、SVM模型等各种可用的预测模型。例如江自强等选择RBF神经网络的现代化建筑用电量智能预测方法、BP神经网络的现代化建筑用电量智能预测方法在相同条件进行对比测试［4］。孙靖等为解决冰蓄冷控制问题，提出了利用季节性时间序列模型进行建模预测的理论和方法［12］。缪灵均等分别采用布朗（Brown）单一参数线性指数平滑法和Holt双参数线性指数平滑模型对2013—2016年煤油和天然气的消耗量进行预测，结果表明指数平滑模型较为有效［8］。欧阳前武等利用ARMA模型（Auto Regressive Moving Average model，自回归滑动平均模型）对广州市区的商业建筑逐月总能耗进行预测，模型预测结果与实际值比较吻合，ARMA模型在短期建筑能耗预测中是一种精度较高的方法［9］。黄荣庚等也是利用ARMA模型对于地铁站环控系统进行能耗，发现预测具有较高的拟合精度［11］。李龙等开展了基于人工神经网络的负荷模型预测研究，对日最大、最小负荷时刻进行负荷模型预测［6］。通过上述分析可知，ARMA模型在能耗预测领域的适用性较强，指数平滑模型也具有较强的可操作性。

但是现有研究成果普遍存在两个问题：一方面，面向企业的用电量预测研究较少，而当前电力市场化背景下，大型企业才是电力需求侧管理和电力市场化交易的主体，因此企业用电量的预测研究亟待加强；另一方面，输入参数较少的预测模型的组合应用不够，预测准确度有待提高，而人工神经网络的预测虽然能提高准确度，但是输入参数过多，需要考虑日最大负荷值、日最小负荷值、负荷平均值、最高最低温度、日平均风速、日期类型等多种影响因子，操作难度大，普适性不够，无法大面积推广应用。

3 模型构建与变量说明

本文以工业企业的用电数据作为分析和预测的对象，特别适合于电网公司需求侧管理、售电公司电力市场化交易、综合能源公司能效管理服务的市场化应用需求，具有非常突出的实践指导意义。本文所建立的模型简单实用，输入参数少，可操作性强，适用性广，实现了电网公司营销数据和企业能耗监测数据的有机结合和深度利用，既有大量可用的数据基础，也有巨大的市场需求，实用价值非常高。

3.1 样本数据分析及预测模型的选择

本文首先采集中山市某企业2019年1月1日—10月31日的逐日用电量为样本进行分析，建立时间序列Y，其时序图如图1所示。

图1 2019年1月1日—10月31日逐日用电量曲线图

企业用电量与企业的产量和经济周期相关度较高。对于非季节性生产企业而言，企业的用电量相对而言较为平稳，春节、黄金周和周末等节假日的用电量通常与常规工作日有所不同。

通过图1可知，该企业的用电量数据属于较为典型时间序列，整体上没有明显增长或减少趋势，除个别节假日以外，数值在10 000～30 000之间随机波动，同时波动范围有界（0≤用电量≤企业变压器的最大容量），因此初步判定企业用电量数据序列属于平稳时间序列。

针对平稳时间序列的预测，较为成熟的模型为线性回归模型、ARMA模型和指数平滑模型，其中线性回归模型通常跟ARMA一起组合应用。这类模型不需要建立因果关系模型，仅需要其变量本身的数据就可以建模，特别适合于企业用电量的预测。而神经网络模型、SVM等模型虽然更先进，但是输入参数过多，各类参数无法自动采集或参数本身就是预测值（例如气象参数），因此可操作性不强。以下将基于ARMA模型和基于Holt⁃Winters指数平滑模型两个方面进行建模、预测和对比分析，所用分析软件为EViews 8.0。

3.2 ARMA模型的构建

ARMA模型即自回归滑动平均模型，是由自回归模型（简称AR模型）与移动平均模型（简称MA模型）为基础“混合”构成。ARMA模型和应用的构建通常分为五个步骤：平稳性检验、模型识别、确定滞后阶数、模型拟合、模型检验。

第一步，采用ADF单位根检验法检验时间序列的平稳性。单位根检验是指检验序列中是否存在单位根，因为存在单位根就是非平稳时间序列了。将数据集通过EViews软件进行ADF检验，结果见表1。

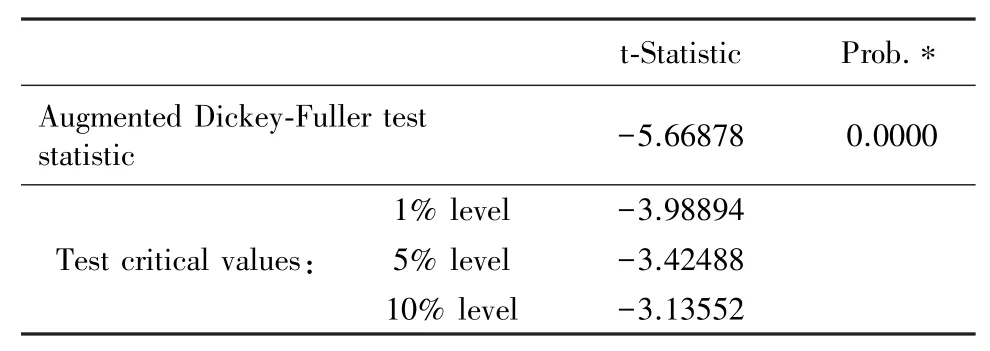
表1 原始序列ADF根检验结果

由检验结果可知，原始序列ADF＝－5.66878＜－3.98894＜－3.42488＜－3.13552，且P值＝0＜1%＜5%＜10%，因此序列Y为平稳时间序列，可进行下一步建模。

第二步，模型识别主要通过检查自相关函数（AC）和偏自相关函数（PAC）。根据序列Y的相关性检验结果，Q统计量的P值均＜0.05，拒绝序列纯随机的假设。同时，AC拖尾和PAC二阶截尾，初步判断可能适合的模型类型为ARMA（2，0）模型。根据序列Y的一阶差分序列相关性检验结果，AC拖尾和PAC均3阶截尾，可能适合的模型类型为ARMA（3，3）模型。

第三步，确定滞后阶数。主要通过AIC、SC和HQ信息准则来判断，取综合最小值确定滞后阶数。由于最复杂可能为ARMA（3，3）模型，因此选取9种排列组合进行比较。即选取ARMA（1，1）、ARMA（1，2）直至ARMA（3，3）这9个模型用最小二乘法进行拟合。拟合后的AIC、SC和HQ信息准则函数值汇总表如表2所示。

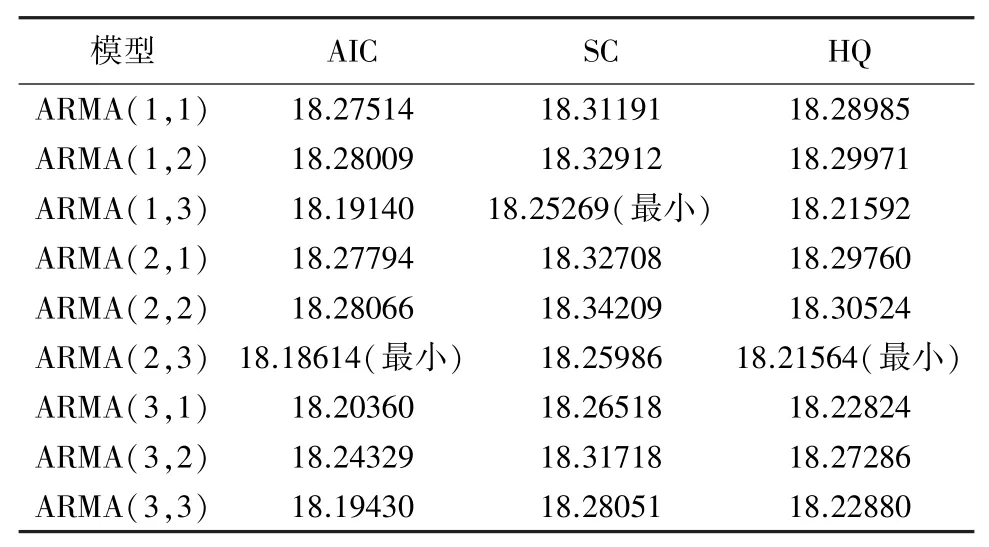
表2 AIC、SC和HQ信息准则拟合结果汇总

通过上表的拟合结果可以判断出，模型ARMA（2，3）下AIC和HQ两个信息准则数值都最小，因此ARMA（2，3）为最优时间序列模型。

第四步，模型拟合。通过多元线性回归与ARMA模型相结合的方式进行模型拟合，这主要是考虑到企业用电量与工作日、节假日、黄金周等工作周期有关，因此需要引入工作日相关的哑变量时间序列。

利用最小二乘法对模型进行拟合后，其参数估计的结果如表3所示。各项参数的P值较为显著，可决系数为0.8018，拟合度较高。

第五步，模型检验。主要通过三种方式进行检验，即通过D⁃W（Durbin⁃Watson，德宾⁃沃森）检验和通过模型残差序列的白噪声检验。

首先，通过D⁃W统计量进行检验。D⁃W检验即杜宾⁃瓦特森检验，是统计分析中常用的一种检验序列一阶自相关最常用的方法。D⁃W统计量的取值范围为区间0～4，当D⁃W统计量趋近于0或4时，序列显著相关；当D⁃W统计量趋近于2时，序列不存在自相关性。根据表3中拟合结果可以看出，D⁃W统计量约为1.89，因此可判定该序列不存在自相关性。

表3 ARMA（2，3）模型与多元线性回归组合拟合结果

其次，对残差序列进行白噪声检验。通过残差序列的自相关性和偏相关性分析可以看出，自相关系数和偏自相关系数在0阶之后，均呈现出截尾的性质，因此可认为残差序列不存在自相关性，为白噪声序列，模型信息提取比较充分，通过模型的适应性检验和显著性检验。

3.3 Holt⁃Winters指数平滑模型的构建

指数平滑法是生产预测中常用的一种方法，也适用于中短期经济发展趋势预测。所有预测方法中，指数平滑是用得最多的一种。简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用，移动平均法则不考虑较远期的数据，并在加权移动平均法中给予近期资料更大的权重，而指数平滑法则兼容了全期平均和移动平均所长，不舍弃过去的数据，但是仅给予逐渐减弱的影响程度。

本文采用EViews 8.0，利用Holt⁃Winters指数平滑模型（非季节性）对企业用电量即时间序列Y进行预测。

如表4所示，通过实验选取不同的平滑指数进行结果分析，发现平滑指数α＝1和β＝0时，残差平方和最小，误差均方根最小，因此选取该参数建立Holt⁃Winters指数平滑模型。

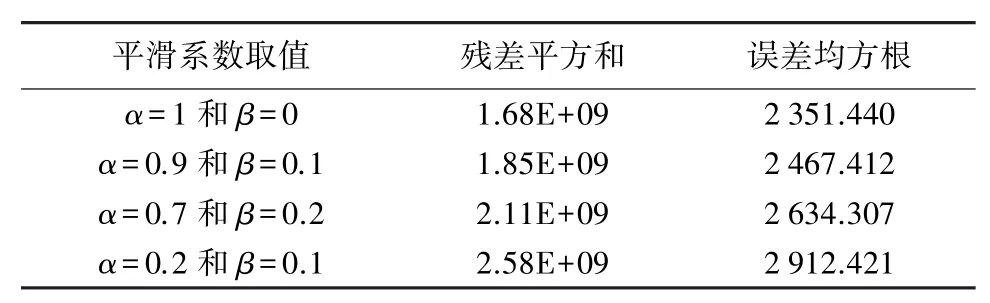
表4 不同平滑系数实验结果比较

4 实证分析

4.1 基于ARMA模型预测的实证分析

4.1.1 分析下一个月逐日用电量预测效果

将前述中山市某企业用电量即时间序列Y对已建立的ARMA（1，3）模型进行拟合度分析，通过比较实际用电量与预测用电量之间的差异，分析预测数据的准确度。以下用2019年1月1日—10月31日数据预测11月1日—11月30日数据，如表5所示。

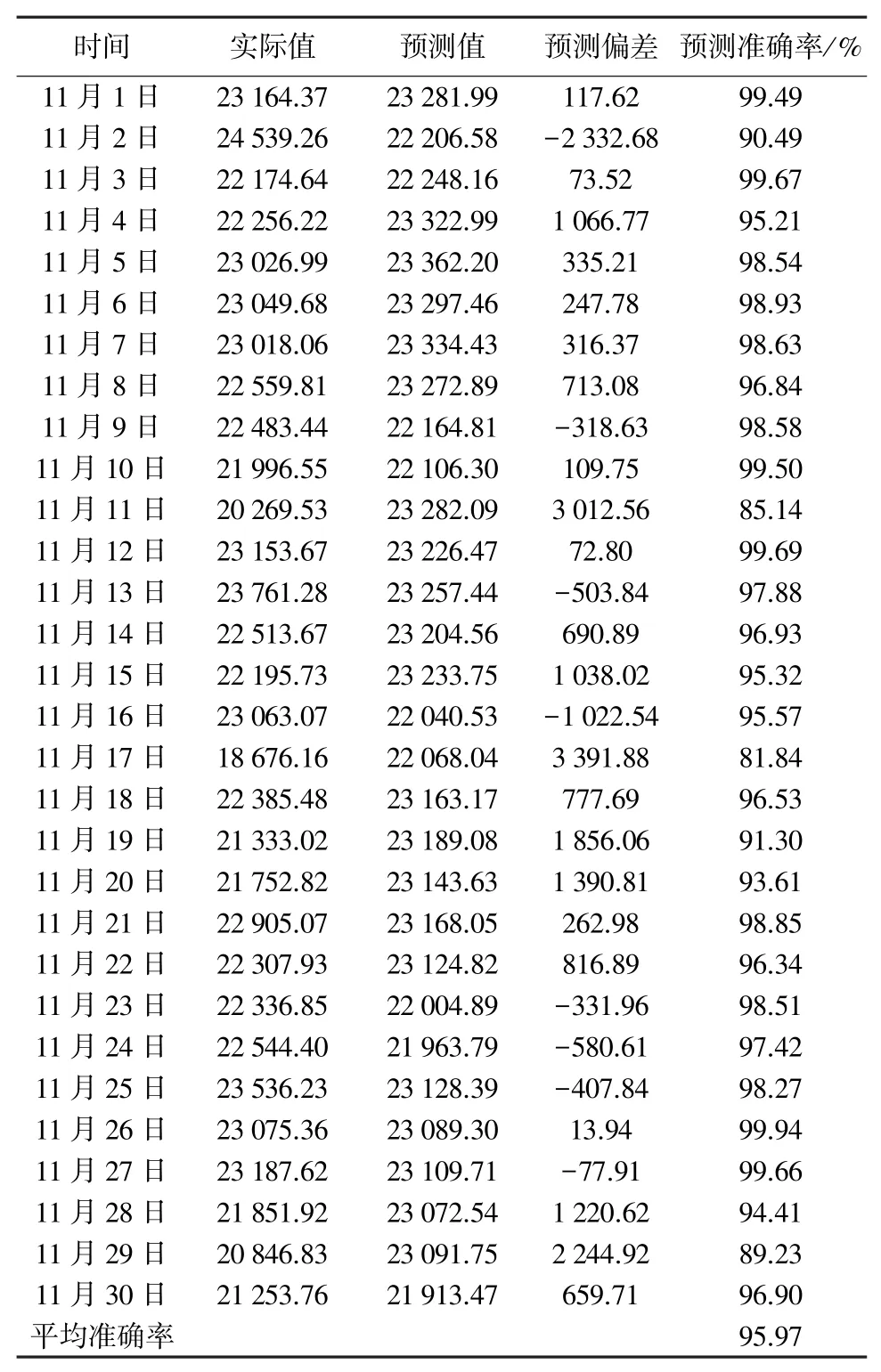
表5 某企业2019年11月1—11月30逐日用电量数据ARMA模型预测

通过上述预测结果可以看出，大部分准确率为98%以上。即便由于少量异常数据的出现，平均预测准确率也达到95.97%，总体预测准确度较高。

4.1.2 分析样本数量对预测准确度的影响

考虑到不同企业可获取的用电量数据时间长短不同，以下针对不同的样本数量进行下个月逐日用电量预测，分析样本数量对预测准确度影响。

本次研究从6个月的数据开始往后递推，即以6个月数据为样本预测第7个月，以7个月数据为样本预测第8个月，直到以10个月数据为样本预测第11个月。

如表6所示，样本数量对于预测准确度具有明显贡献，样本数量越大，平均预测准确度越高。10个月以上的样本数量能够达到95%以上的平均预测准确度。从另一个角度说，针对不同的样本数量，ARMA（n，m）模型中n和m的取值也需要动态调整，实现同等样本数量情况下更高的平均预测准确度。

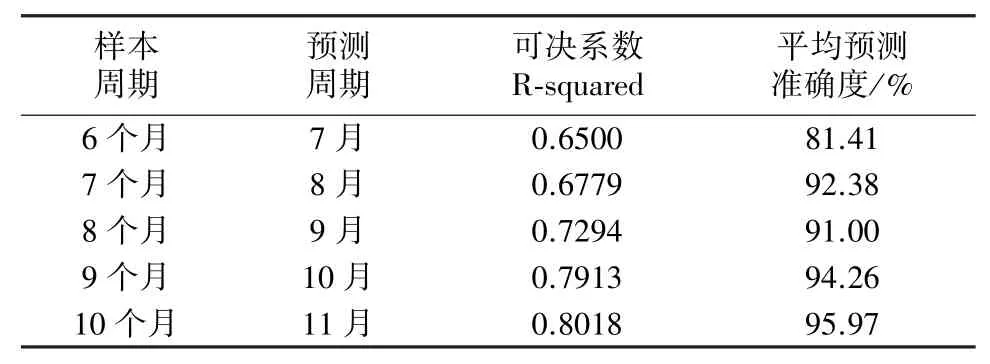
表6 不同样本数量ARMA模型预测结果分析

4.1.3 分析累计日数据作为月数据预测的效果

在当前实际工作中，逐月用电量数据的预测更加具有指导意义，但直接将每月用电量数据作为样本进行预测，样本数较少，准确度欠佳。为此，需要分析累计短期高频数据预测来实现中长期低频数据预测的效果，即分析累计每日用电量的预测数据作为月用电量数据预测的效果。

将上述下月逐日用电量预测的下月30个逐日数据进行累加，形成下月的月用电量预测数据，与下月的实际月用电量数据进行对比，分析预测准确度。

如表7所示，累计高频数据预测中长期数据的准确度较高，预测效果随着样本数量的增加而逐步显著，在9个月以上的逐日用电量数据集进行下一个月用电量数据预测时，准确度已高达97%～98%，已具有较高的现实意义。

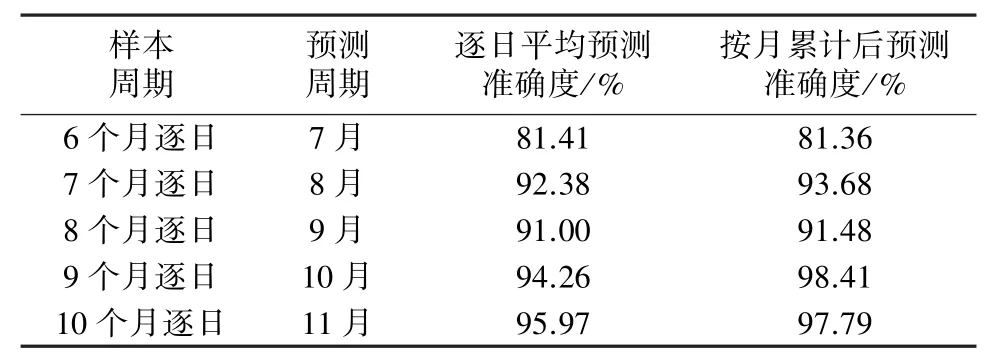
表7 以ARMA模型累计高频数据预测中长期数据效果分析

4.2 基于Holt⁃Winters指数平滑模型预测的实证分析

4.2.1 预测下一个月逐日用电量的效果

将前述中山市某企业用电量即时间序列Y基于Holt⁃Winters指数平滑模型进行拟合度分析，平滑指数α＝1和β＝0，通过比较实际用电量与预测用电量之间的差异，分析预测数据的准确度。以下为该模型预测2019年11月1日—11月30日数据，如表8所示。

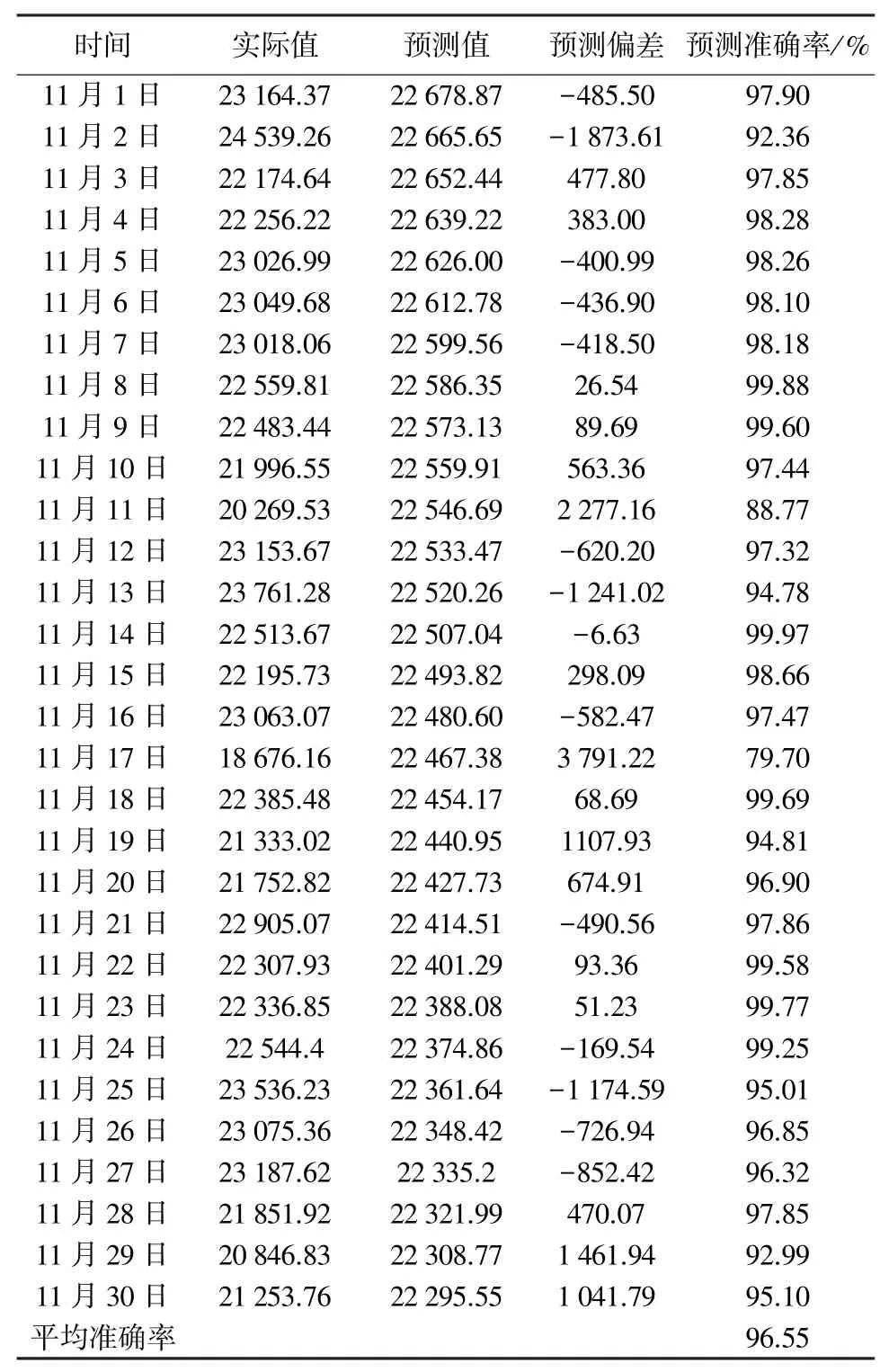
表8 2019年11月1—11月30逐日用电量数据指数平滑模型预测

通过上述预测结果可以看出，大部分准确率为98%～99%以上。即便由于少量异常数据的出现，平均预测准确率也达到96.55%，总体预测准确度较高。

4.2.2 样本数量对预测准确度的影响

针对不同的样本数量基于Holt⁃Winters指数平滑模型进行下一个月的逐日用电量预测。

如表9所示，样本数量对于预测准确度有贡献，超过7个月的样本数量后准确度明显提高，但同时也有一定波动，预测准确度与样本数量不成线性关系。

表9 不同样本数量指数平滑模型预测结果分析

4.2.3 累计日数据作为月数据预测的效果

与前述ARMA模型中的对应分析一样，将所有逐日数据进行累加，形成下月预测数据，与下月实际数据进行对比，分析预测准确度。

如表10所示，累计高频数据预测中长期数据的准确度较高，超过7个月的样本数量后准确度显著提高，4个月的预测中有3个月都达到99%以上，最高达99.84%，具有非常高的现实指导意义。

表10 以指数平滑模型累计高频数据预测中长期数据效果分析

4.3 两种模型的比较

通过将表7和表10联立比较，可以得出表11和表12。

表11 两种模型逐日预测准确度对比分析

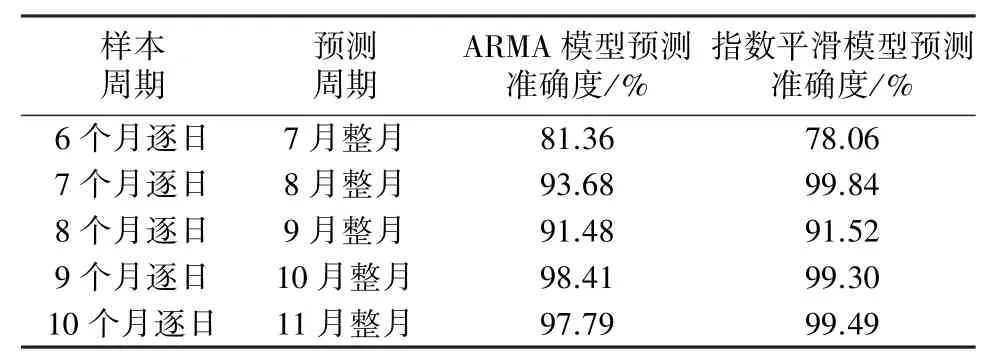
表12 两种模型月累计预测准确度对比分析

由表11和表12可以看出，ARMA模型在预测下个月的每日用电量数据方面具有更高的准确度，而且随着样本数量的增加准确度也继续增加；Holt⁃Winters指数平滑模型预测下个月的每月用电量数据方面具有更高的准确度。

综上所述，ARMA模型在高频数据预测方面比Holt⁃Winters指数平滑模型更有优势，分析其原因主要在于ARMA模型将数据序列看作一个随机序列，这组随机变量所具有的依存关系体现着原始数据在时间上的延续性，而且具有一定的自身变动规律，可以通过回归分析得到较为准确的预测值。这个特点与企业用电量数据的特点非常相似，所以短期高频数据的预测准确度较高。而Holt⁃Winters指数平滑模型兼容了全期平均和移动平均所长，不舍弃过去的数据，但是仅给予逐渐减弱的影响程度，即随着数据的远离，赋予逐渐收敛为零的权数。这个特点使得该模型通过预测高频数据并累加后预测中长期数据的准确度更高。因此在实际工作过程中，两种模型可以组合使用，效果更佳，实用性更强。

5 主要结论

对于工业企业用电量数据预测，基于ARMA模型和基于Holt⁃Winters指数平滑模型预测都较为实用，准确度较高，具有较高的实用价值。基于ARMA模型预测日用电量数据更为准确，基于Holt⁃Winters指数平滑模型预测月用电量数据更为准确，采集样本的数量对于预测的准确度有较大影响。二者组合应用具有较高的可行性和推广价值。