基于矢量分解的三轴高g值加速度计灵敏度系数校准方法

吴倩，郭伟国

(西北工业大学 航空学院, 陕西 西安 710072)

0 引言

多维或多轴加速度计是国防、航空、电子、汽车和机械等领域振动和冲击测量的惯性元件之一，其中高g值加速度计多用于侵彻、穿甲等过程中的冲击载荷测量。由于实际冲击过程复杂，需同时测量三维冲击力，多轴高g值加速度计在国防与民用中测试的是实际结构或材料的真实情况，因此多轴高g值加速度计在工程应用中发挥着重要作用。

一般来说，飞机内黑匣子冲击地面会达到数千的g值过载，高速列车车体遭遇硬质小离散体撞击也会承受数万g值过载，高速侵彻与碰撞过程的加速度则会超过1×105g.在各种动态冲击环境中，实际结构或材料处于三轴高冲击及高g值的环境，自然准确测试需要的是多轴高g值加速度传感器。所以国内外把开发、使用和测试校准多轴高g值加速度传感器一直作为研究重点。

由于高过载的冲击，传感器内部结构、元件或装配等可能会出现变形损伤，导致传感器指标变化，必须要对其性能指标进行校准，同时，对于各种智能敏感飞行器和弹体惯性导航中的高g值加速度计来说，不允许有任何微小的测试偏差。因此，多维高g值加速度计校准成为目前传感器领域研究发展的焦点，在现代工业技术以及未来人工智能发展中是不可缺少的。

目前对于三轴高g值加速度计的校准，国内外尚无统一的标准。现有的校准方法主要有两类：

1)第1类方法是在参考单轴加速度计标定方法的基础上，依次对三轴加速度计每个方向分别校准。然而一般设备无法对高g值加速度计进行校准，由于Hopkinson 压杆不仅能产生几十万g的冲击加速度, 且加载波形可调易控制，目前国内外研究机构主要采用Hopkinson杆法[1-9]来标定。Duan等[5]基于碰撞理论研究了针对高g值加速度计标定的波形整形方法，提出了用于预测加速度幅值和脉宽的理论模型。杨志才等[6]基于一维应力波传播理论和弹性波叠加原理，设计了双弹头Hopkinson杆校准装置，用以实现精确标定高g值加速度计的动态线性参数。Kuells等[8]提出一种采用多个测量点的数据、使用多组试验数据进行标定的方法，该方法适用于多种不同方式的Hopkinson杆法，但只能在2×104g量程范围内。Li等[9]利用Hopkinson杆实现对微机电系统(MEMS)加速度计在最高3.7×104g加速度信号下的冲击校准，测试的平均值与模拟值一致，最大偏差小于5%.

2)第2类方法是同时对三轴加速度计的3个轴进行校准，主要有以重力场翻滚为基础的方法[10-14]和以三轴振动台为基础的方法[15-16]。Won等[10]以及Sipos等[11]基于静止加速度计的输出等于重力矢量，通过把加速计安装在三轴虎钳上，利用旋转获得6个校准参数，通过关联参数的数学模型获得校准方法。Pylvänäinen[12]、Bonnet等[13]先后提出三轴加速度计的椭圆球拟合标定方法，从最大似然估计的角度对其数学变换进行参数辨识。Beravs等[14]使用机械手将三轴加速度计放置在不同的位置和方向，通过协方差矩阵和卡尔曼滤波器对其灵敏度参数进行迭代估算。Umeda等[15]研究用三轴振动台标定三轴加速度计的灵敏度，并讨论了三轴加速度计灵敏度矩阵和单轴加速度计横向灵敏度之间的关系。张俊等[16]针对现阶段对三轴标定台加工精度难达到设计要求的问题，提出一种根据三点调平原理能同时标定三轴加速度计3个轴的振动台，降低了加工精度而提高了标定精度，并提出了一种新的平面解耦方法。

在上述的两类方法中，单轴依次校准方法耗时较长，不能同时同步对三轴加速度计施加相同或不同幅值过载脉冲，且数据处理复杂，难以得到反映各轴之间耦合程度的交叉灵敏度。重力场和三轴振动台方法一般仅用来标定低量程三分量加速度计，无法满足高g值加速度计的校准要求，此外，三轴振动台法必须进行运动解耦，有效的解耦装置设计也是对该方法校准精度的一大考验。

针对上述研究问题，本文基于Hopkinson杆原理以及加速度矢量的分解，通过对Hopkinson标准杆进行斜面设计，并将加速度计置于斜面上，实现运动解耦，来校准多维高g值加速度计参数。

1 多轴高g值传感器特性参数测试的方法

借助Hopkinson杆原理校准多维高g值加速度计灵敏度等特性参数的试验布局如图1所示。首先将标准杆(入射杆)端部制作成斜面形式，根据加速度各个轴间矢量分布，确定加速度计在斜面放置位向，并在斜面做标记，将准备测试或校准的多轴高g值加速度传感器过载安装面粘接或固连在此斜面上。然后通过压气机向储气室充气到预定气压值，打开瞬态撞击杆(弹)发射阀。撞击杆撞击缓冲垫块把类似半正弦弹性应变脉冲传播至标准杆，使得杆端的加速度传感器产生信号，并沿自身的x轴、y轴和z轴分别输出脉冲信号，进而对处于斜面的多维高g值加速度传感器进行冲击加载。

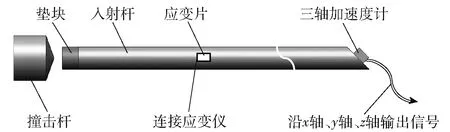
图1 Hopkinson杆校准加速度计试验装置图

测试中，调节储气室气压可改变撞击杆的速度，在垫块和标准杆前端的接触面涂抹薄薄的一层二硫化钼，并用套环连接，以防在撞击过程中垫块掉落或飞穿，在标准杆中部粘贴有高精度应变片以检测冲击应变脉冲。试验中通过对发射杆几何形状设计，实现不同构形的冲击应变脉冲，一般锥形撞击杆会在入射杆上产生近似半正弦的应变脉冲激励信号。对处于Hopkinson杆端部的加速度计施加半正弦的过载信号a(t)，即

(1)

式中：amax、T分别为加速度信号的峰值和脉宽。

积分(1)式得速度脉冲v(t)：

(2)

由于试验中产生的应力波波长远大于标准杆的直径，忽略应力波传播过程中的弥散和衰减[17]。根据一维应力波理论，其标准杆端部的质点速度vb(t)为

vb(t)=2cεi(t)，

(3)

式中：c为标准杆的弹性一维波速；εi(t)为入射杆上的应变脉冲。杆端的加速度历程为

(4)

设入射杆上粘贴的应变片灵敏系数为Sg，动态应变仪对电压信号的放大系数为Kg，则

(5)

式中：Ug(t)为应变片输出的电压信号。本文中，Sg=2.22，Kg=100.

设被测加速度计的灵敏系数为Sa，加速度计外部所用电荷放大器的增益为Ka，输出电压为Ua，则被校加速度计所感受到的加速度值aa(t)为

(6)

积分(6)式得速度脉冲va(t)：

(7)

式中：τ为0～t时间段的某一时刻。结合(4)式和(6)式，积分可得

(8)

(9)

为了具体计算灵敏度系数，选取3组数据，基于(9)式有

为了更直观地表示加速度计轴间耦合程度，常用横向灵敏度比TSR表示加速度计横向效应[18]：

(10)

式中：i=x,y,z，j=x,y,z，且i≠j.

2 多轴高g值加速度计特性参数的测试

2.1 基本原理和理论分析

在Hopkinson杆原理中将标准杆的端部设计为斜面形式，加速度计粘贴在斜面角度为θ的Hopkinson杆斜面端部。如图2(a)所示，当撞击杆撞击产生的应力脉冲传播到斜面上时，可将入射杆所在的整体坐标系Oixiyizi下yi轴方向的脉冲a0(t)沿加速度计内部坐标系的y轴和z轴两个方向进行矢量分解，分别输出沿斜面的切向加速度脉冲at(t)和法向加速度脉冲an(t)。

图2 标准杆端斜面示意图

根据图2(b)的受力分析，结合(4)式，可得产生的加速度脉冲二维关系：

(11)

A=Q″·Q′·AO·Q′T·Q″T.

(12)

结合(4)式和(12)式可得同步加速度脉冲在Oxyz下矢量分解的三分量为

(13)

2.2 数值仿真分析

在图1所示的Hopkinson杆系统中：入射杆和垫块直径均为14 mm，长度分别为1 200 mm和10 mm，材料均为7075铝；撞击杆是由直径为28 mm的圆柱和圆锥组合构成，其中圆柱高度为20 mm，圆锥高度为5 mm.撞击杆材料为45号钢，冲击速度为15 m/s.具体材料参数如表1所示。

表1 材料参数

在数值仿真中，可认为入射杆为一根细长圆柱杆和不同角度斜面的组合，网格划分类型分别为八节点六面体单元(C3D8R)和10节点修正的二次四面体单元(C3D10M)，二者间使用 Tie 连接。模型整体采用通用接触，法向力学行为为硬接触，切向力学行为不考虑摩擦力的作用。

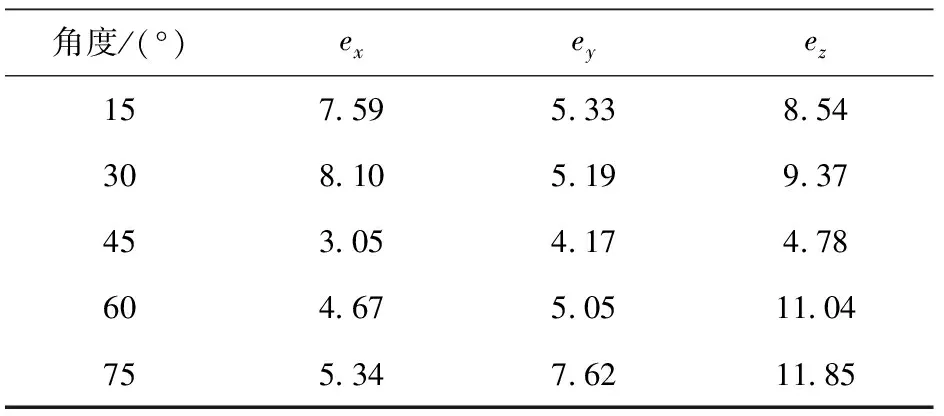
表2 不同角度斜面的误差

从表2中可以看出，在利用斜面的方法校准三轴加速度计时，斜面角度的选择对试验结果存在一定的影响，在一系列的误差对比下，当斜面角度为45°时，误差相对较小。

如图3和图4所示，通过对比斜面角度θ为45°和60°的仿真输出与计算结果，可以看出仿真与计算所得的加速度脉冲较为吻合。在不同斜面角度下，脉冲幅值的三分量均符合矢量分解的关系式，随着斜面角度的增加，加速度脉冲时间均约为90 μs，也就是加速度脉冲的脉宽无明显变化，但幅值会发生改变，因此可以通过调整斜面角度θ来得到不同的加速度脉冲构型。

图3 仿真中θ=45°斜面的输出加速度信号和计算得出加速度信号对比

图4 仿真中θ=60°斜面的输出加速度信号和计算得出加速度信号对比

3 试验验证与结果分析

验证试验使用的三轴高g值传感器为北京大学生产的CA-YZ-100K-T压阻式加速度计，尺寸为13 mm×13 mm×11 mm，可测量1×105g及以下的加速度，非线性不大于10%FS，其中x轴、y轴、z轴的零点输出均应为(0±100)mV，零点漂移均应在-50～50 mV之间。在进行多轴同步校准试验之前，为了进行对比分析，也按照常用的校准方法，先对三轴高g值加速度计进行单轴依次校准，得到每个主轴轴向的灵敏度系数，以便对采用三轴同步校准的灵敏度系数作对比。

3.1 一维平端面标准杆的单轴校准

试验时将三轴加速度计的x轴向与标准杆平面端面(即垂直截面)粘贴重合，施加气压为0.05 MPa，进行加速度计x轴向的过载与测试，也同时测试与加载方向垂直的y轴和z轴的输出，其结果如图5所示。保持所有试验状态相同，同理依次对y轴和z轴进行试验。具体试验结果如图6和图7所示。

图5 x轴向单轴校准的应变片信号与加速度计三分量

图6 y轴向加载的应变片信号与加速度计三分量

图7 z轴向加载的应变片信号与加速度计三分量

应用(8)式和(9)式，对加速度计输出信号积分后与标定杆上应变脉冲信号进行比较，计算得到CA-YZ-100K-T高g值加速度计在8V激励电压下的灵敏度系数为

根据该灵敏度系数对试验结果进行校准，如图8、图9、图10所示，结果较为吻合。已知三轴加速度计的主灵敏度系数为0.732 μV/g，灵敏度误差不超过5%.

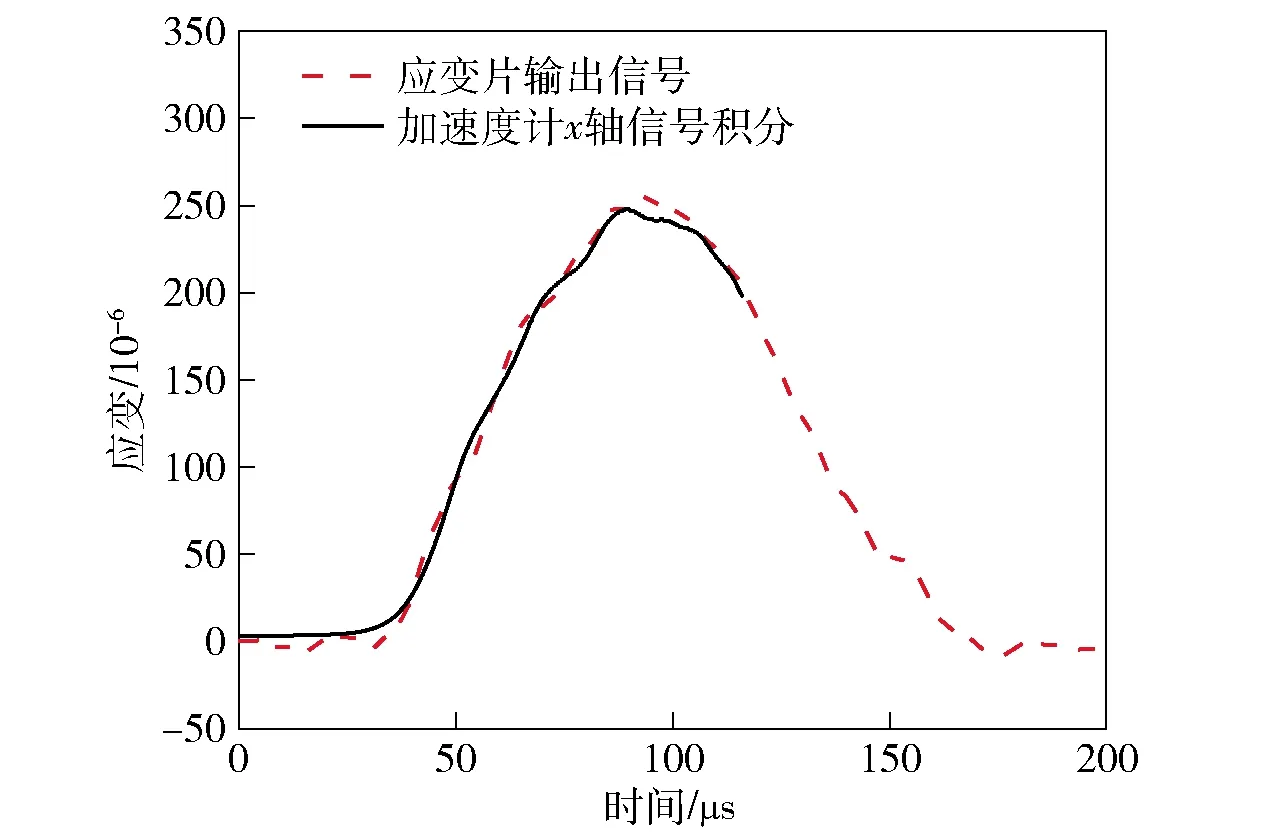
图8 x轴向单轴校准后的应变片信号与加速度信号积分

图9 y轴向单轴校准后的应变片信号与加速度信号积分

图10 z轴向单轴校准后的应变片信号与加速度信号积分

应用(10)式计算加速度计的横向灵敏度比如表3所示。由表3可以看出：在x轴主轴向加载时，y轴向的横向效应比z轴大；在y轴主轴向加载时，x轴向的横向效应比z轴大；在z轴主轴向加载时，x轴向和y轴向的横向效应相差较小。说明x轴和y轴耦合程度较大，z轴耦合程度相对较小，这与加速度计的内部结构有关。

表3 各轴间横向灵敏度比

3.2 一维斜端面标准杆的三轴同步轴校准

将垂直端面杆改换为有一定角度的斜面撞击杆，其他试验测试布局形式不变，实现一次加载同时同步使三轴加速度计过载输出。其中，三轴加速度计如图11所示粘接在斜端面上。

图11 加速度计粘贴方式

根据数值模拟结果，试验中选取Hopkinson杆中标准杆端面斜面角度为45°，φ值取0°、30°、45°、60°，在不同气压下进行多组试验，并根据试验数据对三轴加速度计的主灵敏度系数进行校准，如表4所示。

表4 基于矢量分解的灵敏度系数及误差

图12(a)和图12(c)分别为三轴加速度计和应变片输出的原始数据，图12(b)和图12(d)分别为加速度计的输出经过积分法用试验所得的灵敏度系数校准后与应变片输出三分量进行对比，可以看出曲线吻合良好，证明了这种基于矢量分解对Hopkinson杆进行斜面设计的方法可以对三轴高g值加速度计进行校准。

图12 不同脉宽和角度下加速度计输出与应变信号三分量

三轴高g值加速度计目前的基本内部结构单元是梁-质量块结构[19]，质量块通过悬臂梁连接在硅框架上，当质量块受到冲击时，每个连接质量块的悬臂梁根部的应变电阻均会产生电阻变化，输出不同方向的电压差，从而产生交叉灵敏度。除此以外，在三轴加速度计设计中，零件的加工误差以及加工工艺的精度等均会影响到三轴加速度计的灵敏度系数。

在对三轴加速度计的单轴进行依次校准时，仅考虑主轴方向(单轴方向)，与加速度计的实际结构形式与多轴加速度计在实际应用工作状态不相符合，况且MEMS和微小型多轴加速度计，其内部结构复杂进而明显的三轴方向也需要通过标定与校准装置测试，通过本文提出的Hopkinson杆斜面的矢量分解可以同时得到三方向已知构型的加速度脉冲，同步对三轴高g值加速度计进行校准，充分考虑了在冲击时各种因素导致的垂直主轴加速度输出。

4 结论

本文基于加速度矢量分解对Hopkinson杆斜面设计以校准三轴高g值加速度计，采用Abaqus软件对系统进行数值模拟仿真与基于矢量分解计算对比，通过具体试验验证了该方法的可行性。得出以下主要结论：

1)相较于单轴依次校准，三轴同步校准更符合实际情况，充分考虑三轴高g值加速度计的内部结构以及加工过程等各种因素产生的交叉耦合作用。

2)针对三轴高g值加速度计校准的三维同步脉冲以及轴间耦合问题，采用一维Hopkinson标准杆的斜端面设计，对高g值加速度计三轴灵敏度系数校准，充分考虑三轴主轴与轴间耦合关系，实现同步施加三维过载脉冲。

3)通过三轴加速度计与标准杆斜面端关系，可以实现高g值加速计三轴不同幅值的校准。

4)不同的斜面角度以及加速度安装角度会引起矢量分解变化，对脉冲构型产生影响，运用Abaqus软件进行数值计算，发现最优斜面角度为45°.

5)利用Hopkinson杆斜面设计，基于矢量分解，对北京大学生产的CA-YZ-100K-T压阻式三轴高g值加速度计进行校准，效果良好，从而验证了该校准系统的可行性。